The residual symmetry,Bäcklund transformations,CRE integrability and interaction solutions: (2+1)-dimensional Chaffee–Infante equation

Nursena Günhan Ay and Emrullah Yaşar

1 Department of Mathematics,Faculty of Engineering and Natural Sciences,İstanbul Medeniyet University,34700 Üsküdar,Istanbul,Turkey

2 Department of Mathematics,Faculty of Arts and Sciences,Uludag University,16059 Bursa,Turkey

Abstract In this paper,we consider the (2+1)-dimensional Chaffee–Infante equation,which occurs in the fields of fluid dynamics,high-energy physics,electronic science etc.We build Bäcklund transformations and residual symmetries in nonlocal structure using the Painlevé truncated expansion approach.We use a prolonged system to localize these symmetries and establish the associated one-parameter Lie transformation group.In this transformation group,we deliver new exact solution profiles via the combination of various simple (seed and tangent hyperbolic form)exact solution structures.In this manner,we acquire an infinite amount of exact solution forms methodically.Furthermore,we demonstrate that the model may be integrated in terms of consistent Riccati expansion.Using the Maple symbolic program,we derive the exact solution forms of solitary-wave and soliton-cnoidal interaction.Through 3D and 2D illustrations,we observe the dynamic analysis of the acquired solution forms.

Keywords: (2+1)-dimensional Chaffee–Infante equation,Painlevé truncated exapansion approach,dynamic analysis,Bäcklund transformations,residual symmetries

1.Introduction

Nature’s attractive nonlinearity is the most crucial constraint to comprehending it at its most fundamental level.This approach is widely accepted by researchers.The study of many types of nonlinear ordinary and partial differential equations (PDEs) is essential in the mathematical modeling of complicated systems that fluctuate over time.Physical and natural sciences,neurophysics,population ecology,economics,biomathematics,chemistry,diffusion,biology,heat,and general relativity are all used to develop these models.

Nonlinear evolution equations (NLEEs) can describe many nonlinear physical occurrences in applied science and technology.As a result,finding the exact solutions to the relevant NLEEs is critical for enhancing our understanding of nonlinear events and applying them to practical issues.Therefore,numerous studies have been carried out on this subject [1–7].Many ways for achieving exact solutions to NLEEs have been proposed for example Lie symmetry analysis [8,9],Hirota’s method [10–12],simplified Hirota’s method [3,13],extended tanh method [14] and numerous other techniques [15,16].Some studies to help us understand complex nonlinear wave models,including (2+1) dimensional nonlinear models it is known very recently that N-soliton solutions have been systematically studied by the Hirota bilinear method [12] and by Riemann–Hilbert problems,particularly for higher-order integrable equations[6,7].Furthermore,when it comes to symmetry analysis,the approach plays a significant role in analyzing the properties of PDEs [17–21].Nonclassical symmetry [22],Lie-Bäcklund symmetry [23],and nonlocal symmetry [20] have all been extended from classical Lie symmetries.

Finding the nonlocal symmetries of PDEs is a curious issue.Nonlocal symmetries can give rise to new solutions that Lie point symmetries can not produce [17].The work of [24]presented an approach based on conservation rules for generating nonlocally linked systems in order to achieve nonlocal symmetries.Nonlocal symmetries and nonlocal conservation rules can be investigated by examining nonlocally connected systems [17].New approaches for building nonlocal symmetry theory and producing nonlocal symmetries have been presented over time.Nonlocal symmetries can be generated using methods such as the Darboux transformation [25,26],the Bäcklund transformation [27],and the Lax pairs [26,28].The Painlevé analysis approach,[17,29,30] is a suitable proposed way for revealing the integrability features of PDEs.The truncated Painlevé expansion may be used to build nonlocal symmetries,as presented in [31].Because they are remnants of the truncated Painlevé expansion,such nonlocal symmetries are now known as residual symmetries [17].After examining several interaction solutions created by non-local symmetry reduction analysis,the consistent Riccati expansion(CRE) approach [32] was presented to investigate interactions between the soliton and other waveforms When the CRE technique is used for an integrable equation,it is considered CRE solvable.

One of the aforementioned NLEEs is the Chaffe-Infante model.Suppose that the substance diffuses in a region with concentration u(x,y,z).If ϱ(x,y,z,t) is the diffusion coefficient,then

follows from the diffusion law,where m indicates the amount of diffusion material and ϱ ＞0.Equation (1) and the law of conservation of mass produce

Take ϱ=1 and that the influential factor is g(u)=u3-u.We achieve

where the variable Γ governs the proportional balance of the diffusion and non-linear elements.Hence the (1+1)-dimensional Chaffee–Infante equation is [33]

In this paper,we will look at the (2+1)-dimensional Chaffee–Infante equation (CI),which can be produced in the same way as the above.The (CI) equation [34]

(where α is the coefficient of diffusion and σ is the degradation coefficient) is a popular reaction-diffusion model that explains the physical processes of mass transfer and particle diffusion.It is also necessary to have a field of usage in fluid dynamics,electronic science,and many other fields of science.Another feature that makes the CI equation important is that it is the typical model of infinite-dimensional gradient systems,where the structure of the spherical attractor can be fully explained.Here,bifurcation in a system parameter that indicates the potential’s steepness also increases the model’s attractiveness [35].The CI equation has been studied using the modified Khater method [35],Lie symmetry analysis [36],the first integral method [37],and a variety of other approaches [38,39].

The following is how the paper is organized.Using the truncated Painlevé expansion,we derive the Bäcklund transformation and the residual symmetry of equation (6).To locate the residual symmetry to the localized Lie point symmetry,an expanded system of equation (6) is developed.New solutions are obtained with the help of any seed solution in section 2.In the next section,we study the CRE solvability of equation (6).In section 4 we examine the solitary wave profile and interactions profile of equation (6).In the last section we give some conclusions.

2.Residual symmetry and Bäcklund transformation

In this section,we will derive the residual symmetry of equation (6) using the truncated Painlevé expansion.Due to truncated Painlevé analysis solution of equation (6) is expressed as

where u0=u0(x,y,t),u1=u1(x,y,t),and f=f (x,y,t) [17].Substituting equation (7) into equation (6) and eliminating all of the powers ofprovides us with;

with Schwarzian variables

We can propose the following Bäcklund-type theorem for equation (6) depending on the Schwarzian form.

Theorem 1.If function f is a solution of equation (9),then

is a solution of equation (6).According to nonlocal symmetry theory [17,31] residual symmetry of equation (6) is given by;

We know that equation (9) is invariant under the Möbius transformation [17];

which indicates that f has the point symmetry,taking k=0,l=m=1,n=∈

The transformation

may transform equation (6) into equation (9).To ascertain the residual symmetry group

we must solve the initial value problem given below:

Here infinitesimal parameter is denoted by ∈.We can see here that the solution to equation (16) can not be found.To easily solve the preceding initial value problem,given an expanded system,one can localize the nonlocal symmetry to the localized Lie point symmetry.As a result,the new variables listed below are necessary

Hence we get a prolonged system including (6),(9),(11),and(14).The prolonged system has Lie point symmetry as;

Due to Lie’s first theorem [18,40],the corresponding initial value problem of Lie point symmetry reads

Solving initial value problem given in equation (18) we yield

where ∈is an arbitrary parameter.With the theorem we will provide,we will now assert that it is possible to generate a new solution from an existing one.

Using the finite symmetry transformation given above,one can obtain a new solution from any seed solution of equation (6) and equation (9).

is a solution of equation (6).By using (20),a new solution of equation (6) is expressed as

Example 2.f=tanh(kx+ly+mt) is a solution of equation (9) then

3.CRE solvability

According to the CRE method [17,32] the solution of equation (6) is written as

where u0=u0(x,y,t),u1=u1(x,y,t) and R(w) is a solution of

Riccati equation with s0,s1and s2are arbitrary constants.Plugging equations (23) with (24) into (6) and collecting all the coefficients of the powers of R(w) results in a system of PDEs around u0,and u1.Solving this overdetermined system we get

Hence,equation (6) obviously has the truncated Painlevé expansion solution connected to the Riccati equation equation (24).As a result,we can deduce that the equation (6)is CRE solvable [17,32].We shall now provide the critical Bäcklund transformation theorem.

Theorem 3.If function w is a solution of equation (26),then

is a Bäcklund transformation between w and u which is the solution of equation (6) where R(w) is the solution of the equation (24).

4.Solitary wave and interaction wave solutions of(2+1)-dimensional Chaffee–Infante equation

This section is split into two subsections.Within the structure of w linear function selection,the exact solution profile of the Riccati problem in the form of tanh and the solitary wave profile will be constructed in the first subsection.The w function combines the linear function and the Jacobi elliptic function in the second subsection,representing the solitoncnoidal solution interaction.

4.1.Solitary wave solution

We use a tanh-function solution of equation (24)

to produce the one-soliton solutions of equation (6).We assume the following solution form of equation (26) as

4.2.Soliton-cnoidal wave solutions

To get the soliton-cnoidal wave coactions of equation (6),we begin with

elliptic equation where c0,c1,c2,c3,c4are constants.Inserting equations (31) with (32) into (26) we acquire

The explicit interaction solutions between the soliton and the cnoidal periodic wave may be given in Jacobi elliptic functions using general solution forms of the equation (32).In this section,we will present two specific solutions to equation (32) in order to solve the (CI) equation.

(a) Case 1.We know that

We know that elliptic functions correspond to lemniscate elliptic functions when n=-1.

Following that,it generates to interactionsolution between the soliton and cnoidal wave solutions of equation (6)

(b) Case 2.

In this sub-case we will consider the solution of equation (32) as a rational elliptic function profile given below:

Inserting equations (37) with (33) into (32) and eliminating all coeffciients of powers ofsn(mξ,n),we acquire

Hence,we reach to another interaction solution forms for the equation (6) which is given below

Physical discussion

In this part,the exact solution profiles obtained in this section against the (2+1) dimensional (CI) model have a very important place in the explanations of various kinds of physical phenomena in high-energy physics and electronic science fields.We have presented graphical simulations of exact solution forms in different physical structures with the application of the residual symmetry method and CRE approaches.We examined the dynamic behavior of exact solution profiles with an appropriate selection of parameters in exact solution forms.

Figure 1 illustrated 3D and 2D graphical representations of the u1(x,y,t) given in equation (21),as constructed with∈=0.1,k=-2,l=-1,m=6,σ=2,t=0,y=1.We discovered that u1is a kink-type profile as a result of this investigating.We know that kink waves are rising or descending waves that go from one asymptotic state to another.The kink solution approaches an infinite constant [41].

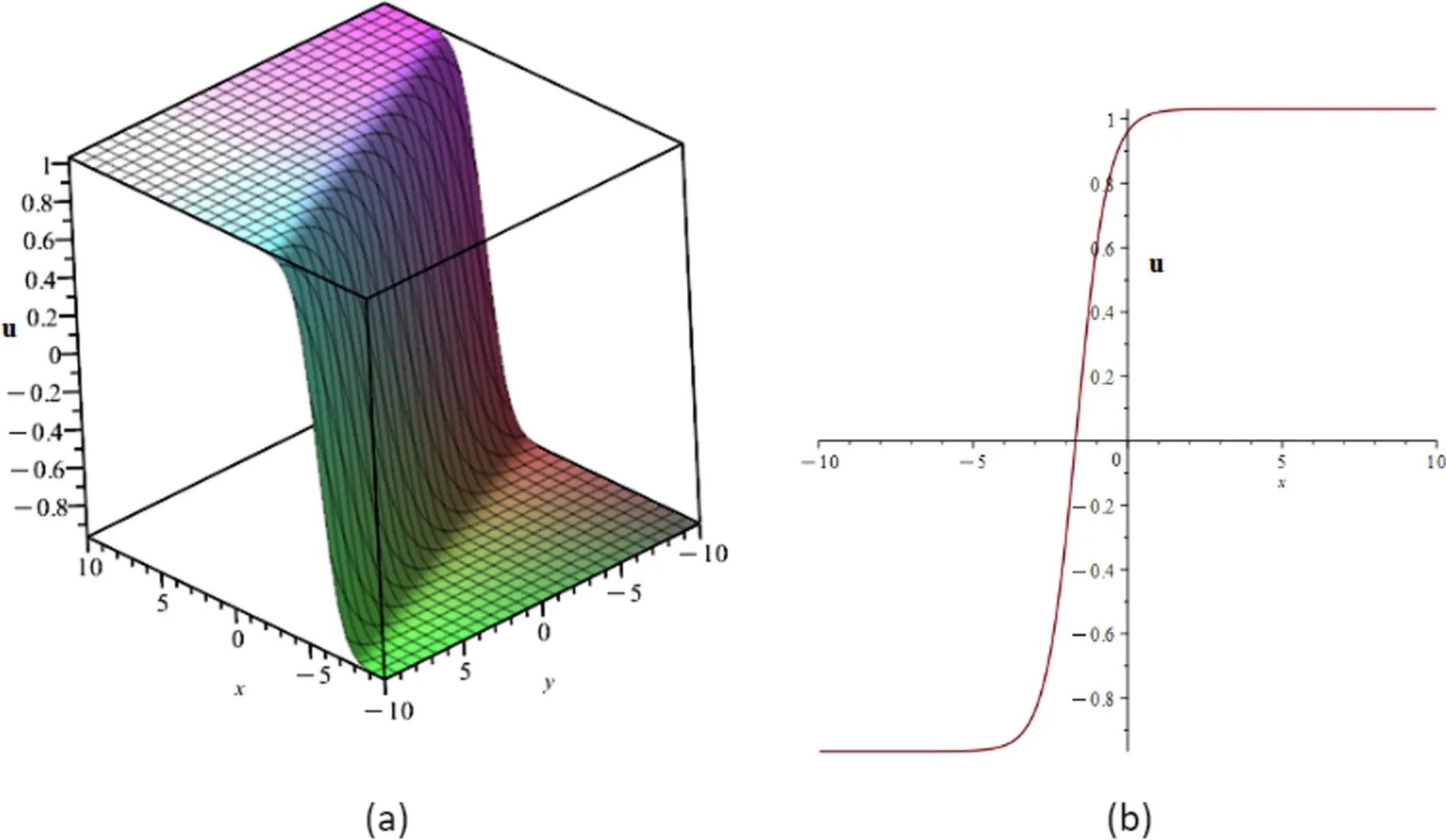
Figure 1.(a) 3D-plot of u1 given in equation (21) where ∈=0.1,k=-2,l=-1,m=6,σ=2,t=0,(b) 2D-plot of u1 given in equation (21)where ∈=0.1,k=-2,l=-1,m=6,σ=2,t=0,y=1.

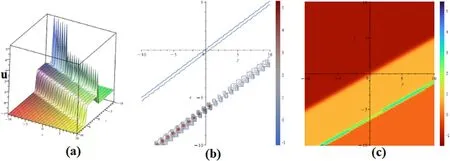
Figure 2.(a) 3D-plot of u4 given in equation (36),(b) Contour-plot of u4 given in equation (36),(c) Density plot of u4 given in equation (36)where s0=1,s1=3,s2=1,p2=0.3,q2=-0.7,η1=1,η0=0.6,α=1,σ=-0.7,x=1.

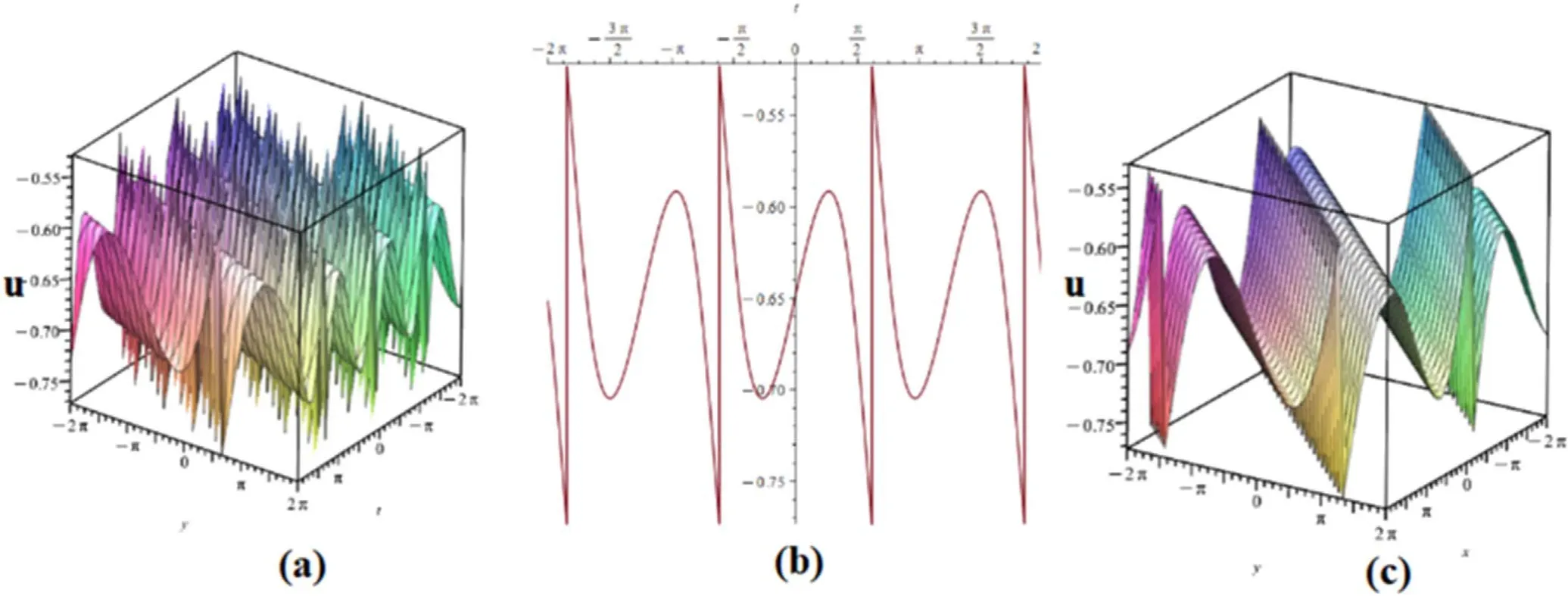
Figure 3.(a) 3D-plot of u5(1,y,t) given in equation (39),(b) 2D-plot of u5(1,1,t) given equation (39),(c) 3D-plot of u5(x,y,1) given in equation (39) where s0=1,s1=3,s2=2,r2=2,q2=-2,r1=1,q1=-1,r1=1,r2=4.5,δ1=1,η0=2,α=1,σ=0.5,η0=-9,ξ0=0.

In figure 2,we presented the 3D,contour and density representations of the u2(x,y,t) interaction given in equation (36),respectively.

In figure 3,the solution u5(x,y,t) given in equation (36),revealed by the interaction of a rational elliptical form solution of the equation (32) and a linear function,is presented together with s0=1,s1=3,s2=2,r2=2,q2=-2,r1=1,q1=-1,r1=1,r2=4.5,δ1=1,η0=2,α=1,σ=0.5,η0=-9,and,ξ0=0.In figure 3 (a),3D representation of u5(1,y,t),in (b) we demonstrate 2D plot of(u5)(1,1,t),(c) 3D plot of u5(x,y,t) at t=1.

5.Conclusion

In this paper,we discussed the (2+1)-dimensional CI model,which is a well-known reaction diffusion equation.First,we applied truncated Painlevé expansion to generate the residual and Bäcklund transformations of the equation.Next,we demonstrated that the Chaffee–Infante equation is CRE solvable.To produce soliton-cnoidal wave solutions,two forms of special elliptic equation solutions are employed.Many important physical phenomena may be explored using soliton-cnoidal wave interaction solutions,including tsunami,and fermionic quantum plasma.Because the investigated equation is (2+1)-dimensional,applying the approaches is very complicated.We feel that these solutions are very distinct from those found in the literature.To the best of our knowledge,the retrieved exact solution profiles and non-local symmetry transformations are new.In addition,we have checked all the constructed exact solutions that satisfy the Chaffe-Infante equation via the Maple package program.

ORCID iDs