Data-driven fusion and fission solutions in the Hirota–Satsuma–Ito equation via the physics-informed neural networks method

Jianlong Sun,Kaijie Xing and Hongli An

College of Sciences,Nanjing Agricultural University,Nanjing,210095,China

Abstract Fusion and fission are two important phenomena that have been experimentally observed in many real physical models.In this paper,we investigate the two phenomena in the (2+1)-dimensional Hirota–Satsuma–Ito equation via the physics-informed neural networks (PINN)method.By choosing suitable physically constrained initial boundary conditions,the data-driven fusion and fission solutions are obtained for the first time.Dynamical behaviors and error analysis of these solutions are investigated via illustratively numerical figures,which show that good results are achieved.It is pointed out that the PINN method adopted here can be effectively used to construct the data-driven fusion and fission solutions for other nonlinear integrable equations.Based on the powerful predictive capability of the PINN method and wide applications of fusion and fission in many physical areas,it is hoped that the data-driven solutions obtained here will be helpful for experts to predict or explain related physical phenomena.

Keywords: Hirota–Satsuma–Ito equation,physics-informed neural networks method,fusion and fission solutions

1.Introduction

With the explosive development of science and technology,deep learning with neural network methods has been widely applied in areas such as cognitive science,computer vision,image recognition,recommendation systems and natural language processing [1–5].Many traditional deep learning algorithms are designed to only solve specific learning tasks[3,6].The huge cost of data acquisition makes the use of traditional deep learning algorithms challenging when applied to complex physics and engineering analysis.In 2019,a new deep learning framework based on physical constraints,namely the physics-informed neural network (PINN),was proposed by Raissi et al [7].The PINN is able to provide accurate solutions even if only a small amount of data is available.Importantly,since some physical constraints are usually explicitly involved,the PINN method can provide a better physical explanation of the predicted solution.Therefore,many scholars have devoted themselves to investigating the PINN method and its variants.For example,by using the PINN method,Chen's group constructed data-driven soliton solutions for three nonlinear evolution equations [8–10].Subsequently,they derived data-driven breather waves and rogue waves for the nonlinear Schrödinger (NLS) and Chen–Lee–Liu equations [11,12].Yan's group obtained data-driven rogue waves for the defocusing NLS equation with a potential[13].Dai's group constructed data-driven femtosecond optical soliton excitations for the higher-order NLS equation [14].Li's group obtained data-driven rogue waves for the NLS equation by using a mix-training PINN method [15].Several other interesting works have also been done in [16–20].

Figure 1.The data-driven fusion solution of the HSI equation at t=0.(a) Density plot.(b) Comparisons of the data-driven fusion solution with the exact one at different y-values.

Solitons,an important type of solution for nonlinear integrable equations,have been widely used in fluid,plasma,optics,condensed matter physics and so on [21].Therefore,many scholars have investigated the soliton solutions of nonlinear systems and a number of interesting results have been achieved.For example,Fan's group discussed the soliton resolution and large-time behavior of solutions to the Cauchy problem for the Novikov equation [22].Yan's group analyzed soliton formation and its dynamic behaviors in quintic nonlinear media [23].Chen's group obtained higher-order soliton solutions to the inhomogeneous variable-coefficient Hirota equation [24].Tian's group derived the soliton solutions of the general n-component and focused on NLS equations [25,26].An's group acquired rich soliton solutions of the Sawada–Kotera equation via the variable separation approach [27].Usually,the interactions between soliton solutions are elastic as their velocity,amplitude and wave shapes remain unchanged during the interaction process.However,for some nonlinear integrable equations,inelastic interactions may occur when the velocities and wave vectors of the solitons satisfy certain conditions.For example,at a certain time,one soliton divides into two or more solitons.In contrast,two or more solitons may fuse into one.The above two phenomena are called soliton fission and soliton fusion in the terminology of soliton theory.Interestingly,is has been found that fusion and fission phenomena exist in many physical areas,such as fluid,plasma,nuclear physics,evenclumping DNA,organic membranes and macromolecule materials,as well as Sr–Ba–Ni oxidation crystals and waveguides [28–31].Therefore,it would be of great interest to look for fusion and fission solutions in nonlinear integrable equations.

After surveying the existing literature,we found that no work has been done on data-driven fusion and fission solutions of nonlinear integrable equations.In particular,no such work has yet been done using the PINN method.Therefore,in this paper,we plan to investigate data-driven fusion and fission solutions in the (2+1)-dimensional Hirota–Satsuma–Ito (HSI) equation by the PINN method,which is described by:

This equation was introduced by Hirota and Satsuma to model unidirectional shallow water waves [32].Due to its importance and wide applications,the HSI equation has been studied extensively and various exact solutions have been constructed,such as complexiton solutions [33],semi-rational solutions [34],rational localized waves and their absorb–emit interactions [35],multi-wave,breather-wave and hybrid solutions [36],resonant multi-soliton solutions [37],and symmetric invariant solutions [38].Unlike the above work,our aim is to construct data-driven fusion and fission solutions for the HSI equation using the PINN method.

The outline of this paper is organized as follows.In section 2,we briefly give the PINN deep learning method for the HSI equation (1.1).In section 3,by choosing suitable physically constrained initial boundary conditions,abundant data-driven fusion and fission solutions of the HSI equation are obtained via the PINN method.Numerical simulations show that such solutions take the shape of the capital letter Y in spatial structures.The error analysis reveals that our obtained data-driven fusion and fission solutions can rapidly approximate the exact ones derived by Tian and his coauthors[39].Therefore,we conclude that the PINN method is a very effective algorithm for constructing the data-driven fusion and fission solutions for nonlinear equations.Finally,a short conclusion is provided.

2.The PINN method

The general form of a (2+1)-dimensional coupled system with three components can be written as

where u,v and w are real-valued functions with variables x,y and t,and Nu,Nvand Nware the functions associated with the real-valued solutions and the derivatives of each order with respect to x and y,respectively.According to the principles of the PINN method,we define the physicsinformed neural networks fu,fvand fwas

where Nu,Nvand Nware the physical models given in (2.1)and u(x,y,t;ω,b),v(x,y,t;ω,b) and w(x,y,t;ω,b) are latent functions of deep neural networks with the weight parameter ω and bias parameter b,which can be used to approximate the exact solution u(x,y,t),v(x,y,t) and w(x,y,t) of the objective equations.Then,by using multi-hidden-layer deep neural networks,the network parameters of the latent functions u,v and w and networks fu,fvand fwcan be constantly trained.

In the following,in order to obtain the optimum training results,we adopt the limited-memory Broyden–Fletcher–Goldfarb–Shanno optimization algorithm [40] to minimize the whole mean squared error,namely,the loss function

Note that,without loss of generality,this paper selects the hyperbolic function tanh as the activation function (if there are no special instructions).All codes are based on Python 3.6 and tensorflow 1.10,and numerical experiments are run on an HP Pavilion Laptop 14-bf1xx computer with a 1.60 GHz Intel Core i5-8250U processor and 8 GB memory.

3.Data-driven fusion and fission solutions of the HSI equation

The initial boundary value problem with a Dirichlet condition for the (2+1)-dimensional HSI equation takes the following form:

With the aid of the Hirota bilinear method [41–43],the N-soliton solution of the HSI equation (1.1) can obtained via

As shown in [39,44],when requiring the parameters eAijgiven in (3.4)

which is equivalent to

then expression (3.2) represents the fusion (or fission)solution consisting of M-fusion (or fission) and L-fusion (or fission) solitons.

In the following,we shall adopt the PINN method given in the above section to construct the data-driven fusion and fission solutions for the HSI equation with Dirichlet condition (3.1).

3.1.Data-driven pure fusion (fission) solution with N=2

Here we consider the case of N=2.When setting L in (3.5) to be zero and selecting the parameters as

we can obtain a pure exact fusion solution,which is described by

Let the spatial region Ω=[-15,15]×[-15,15] and time region [t0,t1]=[-5,5].By substituting u0(x,y,t)=u1(x,y,t),v0(x,y,t)=v1(x,y,t) and w0(x,y,t)=w1(x,y,t) into (3.1),the initial boundary value problem can be solved.To acquire the training data,the finite difference method is employed,in which the spatial and time regions are divided into 65 × 65 and 33 points,respectively.Then,we randomly pick Nu=Nv=Nw=100 points from the original initial boundary data and Nf=10000 collocation points to generate a small training data set by using the Latin hypercube sampling (LHS)method [45].According to the obtained training data,by using a nine-layer feedforward neural network with 20 neurons in each hidden layer,the data-driven pure fusion and fission solutions are successfully learned by regulating the network parameters and minimizing the loss function.

Below,we present numerical simulations that validate the effectiveness and accuracy of the obtained solution.The dynamic behaviors of the data-driven pure fusion solution by the PINN method are depicted in figure 1 and behaviors of the data-driven pure fission solution are exhibited in figure 2.From these figures,one can easily see that with x increasing,the phenomenon of fusion occurs in figure 1(a) and the phenomenon of fission happens in figure 2(a),which takes the shape of the capital letter Y.In addition,observations of figure 1(b) and figure 2(b) show that the errors between the predicted solutions and exact ones are quite small.In fact,for the fusion solution,the L2relative error between the learning solution and the exact one is 8.569428 × 10-3,which takes 280.1288 s learning time.For the fission solution,the L2relative error is 1.708373 × 10-2,which speeds up the 402.3156 s learning time.Therefore,we can conclude that its prediction performance is rather good.In other words,the PINN method is an effective algorithm for constructing the data-driven pure fusion and fission solutions for the HSI equation (3.1).

3.2.Data-driven X-type soliton solution and two interaction solutions with N=3

Here we consider the case of N=3.On setting the parameters as

and inserting them into (3.3),then we can obtain an exact Xtype soliton solution,which takes a form of

Figure 2.The data-driven fission solution of the HSI equation at t=0.(a) Density plot.(b) Comparisons of the data-driven fission solution with the exact one at different y-values.

with

In the above,ηi(i=1,2,3) is described by (3.4).

Taking the spatial region Ω=[-15,15]×[-15,15] and time region T=[-10,10].On inserting them into the expression of (3.10),the initial boundary conditions of the HSI equation (3.1) can be obtained.After that,we discretize the spatial region [-15,15]×[-15,15] into 65 × 65 points and the time region [-10,10] into 33 points with the aid of MATLAB.Then,the initial boundary value data set,namely the training data set,can be generated by randomly selecting Nu=Nv=Nw=500 points from the original data set and choosing Nf=15000 collocation points by using the sampling method given in section 3.1.Inputting the training data set into a nine-layer feedforward neural network with 40 neurons in each hidden layer,we successfully get a data-driven solution of the HSI equation (3.1),which has a L2relative error of 3.170034 × 10-2after 2356 times iteration in 2184 s.

The dynamic behaviors of the data-driven solution of the HSI equation by using the PINN method are depicted in figures 3(a) and (b).From these two figures,one can easily see that with x increasing,the learning solution fuses first and then splits rapidly.Since this kind of solution takes the shape of capital letter X,we can call it the data-driven X-type soliton solution.Figure 3(c) exhibits the dynamic behaviors of the exact X-type solution.A comparison of the predicted solution with the exact one is shown in figure 3(d).From the comparison,one can easily find that a very good prediction performance is achieved in the data-driven X-type solution.

Figure 3.The data-driven X-type soliton solution of the HSI equation at t=0.(a) Density plot.(b) 3D diagram of the predicted solution.(c)3D diagram of the exact solution.(d) Comparisons of the predicted solution with the exact at different y-values.

Now,we shall show that when N=3,except the datadriven X-type soliton solution given in the above,another two kinds of data-driven interaction solution can be generated once appropriate parameters are chosen.To show this,we set the parameters as

According to (3.3),(3.4) and (3.5),the exact interaction consisting of fusion and a single soliton is obtained,which is expressed by

By implementing the same data acquisition and training procedures as that for the X-type data-driven solution,we can get the data-driven interaction solution between fusion and a single soliton,which has a L2relative error of 2.226418 × 10-2after 3297 times iteration in 2861 s.In addition,we can obtain the data-driven interaction solution between fusion and a single soliton with L2=2.263019 ×10-2after 2880times iteration in 1299 s.

Figure 4 shows the dynamic behaviors of the data-driven solution mixed by fusion and a single soliton via the PINN method as well as the comparison of the predicted solution with the exact one.Figure 5 displays the dynamic behaviors of the data-driven solution consisting of fission and a single soliton as well as the comparison of the learning solution and the exact one.From the comparison of figure 4(b) and figure 5(b),we can find that the learning effect is quite good.Therefore,we conclude that the PINN method is very effective to construct data-driven solutions of fusion and fission types.

Figure 4.The data-driven interaction solution between fusion and a single soliton of the HSI equation at t=0.(a) Density plot.(b)Comparisons of the predicted solution with the exact at different y-values.

3.3.Two different types of data-driven interaction solution with N=4

It is known that when two different solitons move towards each other,interactions usually occur,which is an important and interesting phenomenon worthy of investigation.In the following,we shall study whether such interactions can occur between two different data-driven fusion solutions and between data-driven fusion and a soliton molecule.For this purpose,we take N=4 and require the parameters to be chosen as

Inserting these parameters into (3.3) and (3.4) yields that

with ηiand Aijgiven in (3.4).Accordingly,we obtain an exact interaction solution consisting of two different fusions:

Using the same data discretization method in the above,we get the initial boundary value data set with the spatial region [-20,20]×[-20,20] dividing into 65 × 65 points and time region [-10,10] into 33 points.Then,with the aid of LHS,we obtain a training data set by randomly sampling Nu=Nv=Nw=1000 in the original data set and selecting Nf=20000 collocation points.Inputting the training data set into a nine-layer neural network with 40 neurons per layer,we successfully generate a data-driven interaction solution combined with two different fusion solitons,in which the L2error is 6.369453 × 10-2compared with the exact solution.The whole learning process takes about 2419 s and iterates 1977 times.

Figure 6 displays the two-dimensional cross-sectional view of the data-driven interaction solution composed of two fusions,three-dimensional profiles and the corresponding error between the predicted solution and exact one.From figure 6(a),one can clearly see the ‘fusing’ features and the‘interacting’ features in the predicted solutions.In addition,we can also find from figure 6(c) that excellent learning performance has been achieved.

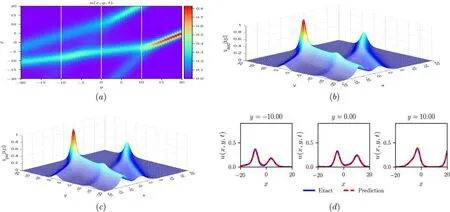
Figure 6.The data-driven interaction solution between two fusions of the HSI equation at t=0. (a) Density plot. (b) 3D diagram of the predicted solution. (c) 3D diagram of the exact solution.(d) Comparisons of the predicted solution with the exact at different y-values.

Figure 7.The data-driven interaction solution between fusion and a soliton molecule of the HSI equation at t=0.(a) Density plot.(b) 3D diagram of the predicted solution.(c) 3D diagram of the exact solution.(d) Comparisons of the predicted solution with the exact at different y-values.

In the following,we shall derive the data-driven interactions between fusion and a soliton molecule in the HSI equation.Thus,we require that one pair of solitons satisfies the velocity resonant principle [46] and the other pair of solitons satisfies the condition described by (3.5),namely:

On setting the parameters as

then a special exact interaction mixed by fusion and a soliton molecule is generated,which is governed by

where

with ηiand Aij(i,j=1,2,3,4) described by (3.4).It is noted that the form of expression (3.20) is quite different to (3.16)for the interaction solution mixed by two fusions.

By performing the same data acquisition and training procedures as used in this subsection,we can successfully obtain the data-driven interaction solution between fusion and a soliton molecule,whose dynamic behaviors are displayed in figures 7(a) and (b).From these two figures,one can easily see that there indeed exists two solitons in the learned solution,which are bounded to form the soliton molecule,while the other solitons fuse to one,just as what happens in the exact solution depicted in figure 7(c).Their comparisons are given in figure 7(d).In fact,the L2relative error for the learned solution is 5.363313 × 10-2,which means a good performance is achieved.Therefore,we conclude that the PINN method is an excellent method to predict the hybrid solution composed of fusion and a soliton molecule for the HSI equation.

4.Conclusion

Fusion and fission are two very important physical phenomena,which have been observed in many fields,such as fluid physics,plasma physics,biophysics,nuclear physics,organic membranes and life science.In this paper,we investigate the fusion and fission phenomena in the (2+1)-dimensional HSI equation.By introducing suitable initial boundary values conditions and physical constraints,we successfully obtain the data-driven pure fusion and fission solutions by the PINN deep learning approach.Numerical simulations show that the data-driven fusion and fission solutions take the shape of the capital letter Y in the spatial structures.In addition,we also derive some data-driven interaction solutions,including the interactions between fusion and a single soliton,between two different fusion waves,and between fusion and a soliton molecule.Numerical error analysis reveals that the data-driven fusion and fission solutions as well as the interaction solutions can rapidly converge to the exact ones given by Tian and his coauthors.Therefore we demonstrate that the PINN deep learning method is a very effective algorithm to solve fusion and fission solutions of nonlinear integrable equations,especially for the HSI equation.Due to the excellent predictive performance of the PINN method,we hope that the datadriven fusion and fission solution derived here can elucidate qualitative features of the HSI model and the physical situation itself.In addition,based on the wide applications of fusion and fission in many physical areas,it is hoped that the data-driven solutions obtained here can be helpful for experts to explain or predict some related physical phenomena.

Acknowledgments

The authors would like to express their sincere thanks to the reviewers for their kind comments and valuable suggestions.This work is supported by the National Natural Science Foundation of China under grant Nos.12371250 and 12205154,Jiangsu Provincial Natural Science Foundation under grant Nos.BK20221508 and BK20210380 and Jiangsu Qinglan High-level Talent Project and High-level Personnel Project under grant No.JSSCBS20210277.