基于模糊层次分析法的网络安全检测评估模型研究

张思齐 赵泰 蒋敏慧

(中国信息通信研究院安全研究所,北京 100191)

0 引言

近年来,随着全球数字经济的蓬勃发展,网络安全威胁持续加剧、攻击手段日新月异、新业务新技术范畴逐步扩展,网络安全的基础性、关键性作用更加突出,网络安全能力建设已成为世界主要国家战略博弈重点领域。为指导网络运营者落实网络安全主体责任,合理配置资源,采取适度、有效的网络安全防护,网络安全等级保护制度、电信网和互联网网络安全防护体系等均采用分级化的合规管理策略,针对性开展补短板锻长板工作。网络安全合规判定是一个多因素耦合的、存在多不确定性的复杂机制,尤其在测评指标权重设定方面,传统的定性分析、定量计算的方法具有较大的主观性和不确定性,难以精确求解,本文根据模糊数学理论,创新性采用模糊层次分析法,建立层次结构模型,根据模糊层次分析法计算权重指标向量,并以网络安全能力成熟度评价体系为例进行数据验证,可以有效解决上述问题,使评价相对科学合理。

1 模糊层次分析法

模糊层次分析法是将模糊数学与层次分析法相结合的一种决策分析方法[1-4],由于实际问题受到多种因素的影响,各因素间往往存在着相关关系,通过从实际问题中分解出相关的关键指标因素,构建层次结构模型,经专家经验判断,对各因素进行两两比较,构造出模糊互补判断矩阵、模糊一致性判断矩阵。然后,利用代数矩阵特性,计算出各层关键因素的权重以及组合权重,最终形成综合决策,从而提高决策的科学性和可靠性。模糊层次分析模型架构如图1所示。

从数学计算角度上看,模糊层次分析法主要包括两个步骤。一是建立模糊互补判断矩阵的过程,设矩阵R=(rij)n×n,0≤rij≤1(i=1,2,…,n;j=1,2,…,n)为模糊矩阵,若模糊矩阵R=(rij)n×n满足rij+rji=1(i=1,2,…,n;j=1,2,…,n),那么模糊互补判断矩阵R建立成功;二是建立模糊一致性矩阵的过程,若模糊互补矩阵R=(rij)n×n,对任意k均满足rij=rik-rjk+0.5,那么模糊一致性矩阵R建立成功。

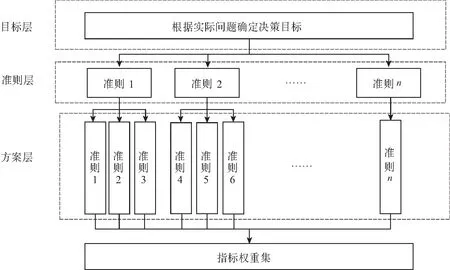
图1 模糊层次分析模型架构

2 基于模糊层次分析法的权重计算

模糊层次分析法具体步骤包括:建立模糊层次结构模型;构建模糊互补判断矩阵;转换得到模糊一致性矩阵;确定单层指标权重并进行一致性检验;确定组合指标权重并进行一致性检验。

利用特征根法对模糊一致性矩阵进行权重排序,具体步骤如下。

(1)计算矩阵R每一行的乘积,即:Mi=ri1×ri2×…×ri(n-1)×rin。

由于评价过程具有一定的人为主观性,为了减小误差,提高结果精度,需要进行一致性检验,具体步骤如下。

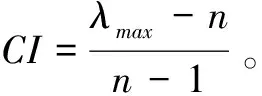
(6)根据不同阶数的判断矩阵,查表1可得对应的平均随机一致性指标(Random Index,RI)。

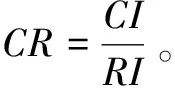
表1 1～10阶重复计算1 000 次的平均随机一致性指标RI表

当CR<0.1时,通常认定判断矩阵的一致性是合理的;CR>0.1时,通常认定判断矩阵的一致性要求不满足,需要重新修正相关的判断矩阵。

得到单层指标权重排序后,采用相同的方法,逐层逐步确定层次总权重,对总排序结果同样也要进行一致性检验。

3 实例分析

本文以电信网和互联网网络安全能力成熟度评价(简称“能力成熟度评价”)作为体系案例,利用模糊层次分析法科学判定成熟度指标权重,验证其可用性。

3.1 构建层次结构模型

能力成熟度评价体系,设A为运营者网络安全能力成熟度水平[5],选择10 个关键因素作为成熟度评价指标,并进一步细化得到两级评价指标因素集。一级指标的因素集B=(B1、B2、B3、B4、B5、B6、B7、B8、B9、B10)=(制度管理、组织和人员管理、资产管理、风险管理、供应链安全管理、系统和通信防护、运行维护、检测评估、安全态势分析、网络安全事件管理)。对一级指标进一步细化分解为26 个领域,得到二级指标Bij的因素集(见表2)。

根据以上分析,可以得到对应的层次结构模型如图2所示。

3.2 确定权重指标向量

本文采用专家评分法确定评价指标体系中每个指标的权重,首先针对特定的运营者P及运营者Q,构建专家调查表,面向运营者、测评机构及行业专家发放调查表,采用0.1～0.9九级标度法对其中同层次同隶属关系的各指标,进行两两因素之间的相对重要性比较评分,具体参见表3。

根据专家调查问卷数据,按照前文计算方法,分别得到运营者P及运营者Q的一级指标权重W(P_1)、W(Q_1)结果如表4所示。

进一步构建二级指标调查问卷,以运营者P为例,针对二级指标进行专家打分,按照前文计算方法,得到运营者P二级指标权重集W(P_2),结果如表5所示。

3.3 结果分析

经对比采用模糊层次分析法得到的运营者P及运营者Q的两组权值,各不相同。一方面,模糊层次分析法可为不同类型运营者提供“定制化”的权值指标,有利于体现不同评价对象的差异性,比如运营者P侧重自身安全防御能力,运营者Q侧重对外提供网络安全服务,根据运营者安全战略重点调整权值指标,更有利于客观评价不同类型运营者的安全能力水平。另一方面,各项权值变化区间控制在一定范围,不同类型运营者,虽然各项权值存在差异性,但是整体能力上看可以进行同质化评价,对最终的等级判断影响较小。综上所述,模糊层次分析法充分利用模糊数学、代数矩阵重要性标度:0.9表示两个元素相比,i比j极端重要;0.8表示两个元素相比,i比j非常重要;0.7表示两个元素相比,i比j明显重要;0.6表示两个元素相比,i比j稍微重要;0.5表示两个元素相比,i与j具有同等重要性;0.4表示两个元素相比,j比i稍微重要;0.3表示两个元素相比,j比i明显重要;0.2表示两个元素相比,j比i非常重要;0.1表示两个元素相比,j比i极端重要。

表2 指标因素集

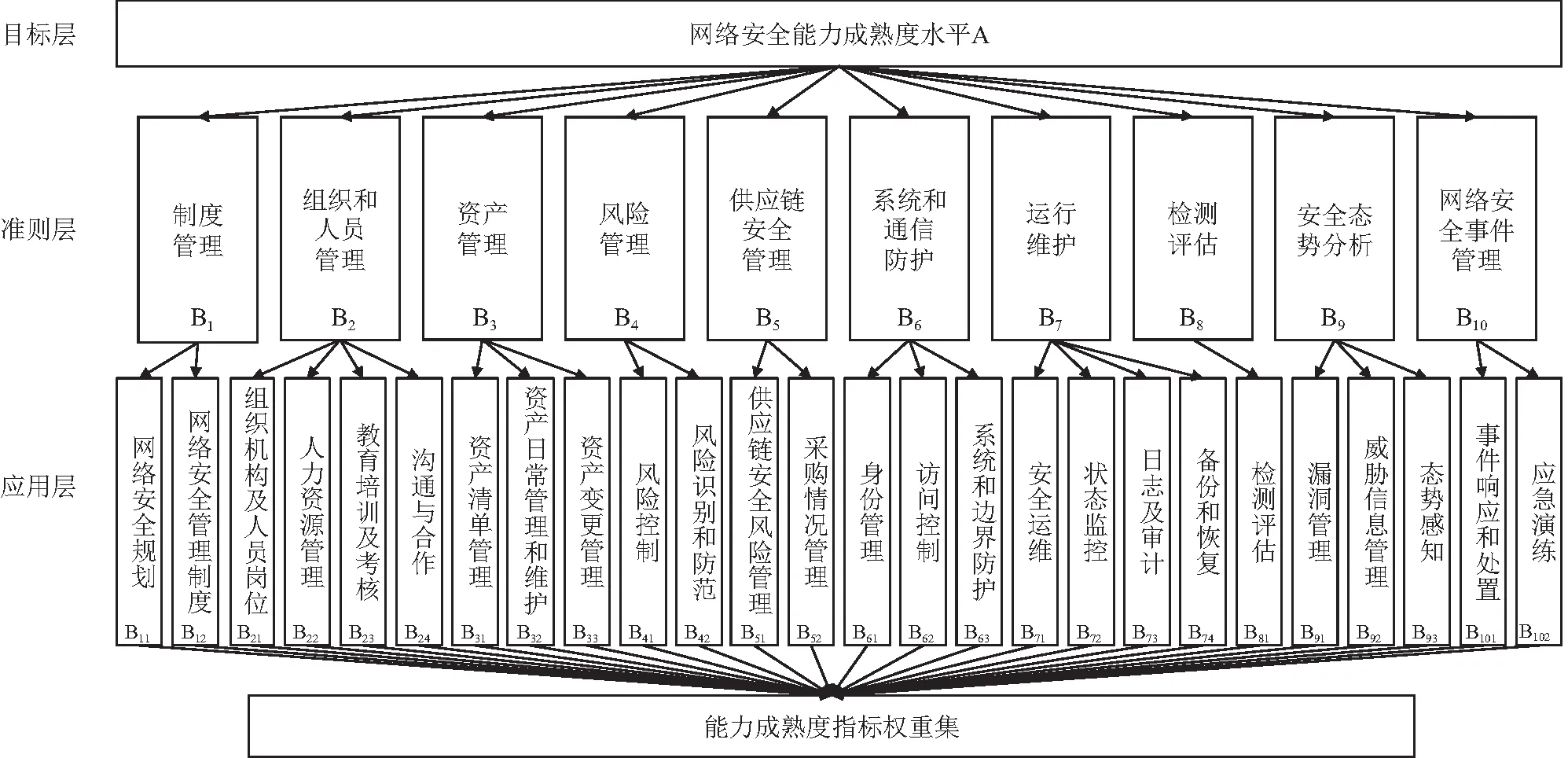
图2 层次结构模型

表3 专家调查表

表4 一级指标权重

表5 二级指标权重集

等特性,有效弥补传统统一赋值法的不足,解决可变参数法可能导致的主观性和不确定性问题,为网络安全能力测评指标权重的科学评判,提供了一种可行的方法及依据。

4 结束语

网络安全检测评估体系往往涉及的指标参数较多、较复杂,评价过程中往往存在主观因素,运用模糊层次分析法能够将人的主观经验判断与数学理论的严谨推理有效结合,从而解决评价过程中模糊、难以量化、非确定性等问题。本文采用模糊层次分析法,重点解决网络安全检测评估体系中测评指标权重赋值难问题,并以能力成熟度评价模型为例,对该模型中不同运营者的10大项26个关键网络安全指标进行赋值测算,达到了预期效果,有效验证了该方法的可行性。在后续模型的使用中,对于测评指标更多、更复杂的情况,未来将继续探索引入专家权重系数和三角模糊数等,对现有模型进行改进优化。