引水隧洞复杂裂隙围岩高压灌浆浆液扩散过程研究
2023-12-05窦金熙赵卫全周建华
窦金熙,赵卫全,路 威,周建华
(1.中国水利水电科学研究院,北京 100038;2.流域水循环模拟与调控国家重点实验室,北京 100038;3.北京中水科工程集团有限公司,北京 100048)
1 研究背景
近来,随着我国抽水蓄能电站的兴建,作为引水系统重要组成部分的压力隧洞正向“洞线长、洞径大、埋藏深”的方向发展,隧洞围岩和岔管区承受较高的压力水头,如天荒坪抽水蓄能电站压力隧洞承受最大静水头680 m,动水头超过800 m;惠州抽水蓄能电站和宝泉抽水蓄能电站承受最大静水头均超过600 m。在超高水头作用下,隧洞围岩的稳定性至关重要,由于各种复杂及难以预测的地质条件影响围岩的稳定性,如何采取有效措施以保持围岩的稳定性,成为制约抽水蓄能电站工程建设中的关键性问题[1]。对隧洞围岩进行高压固结灌浆是处理围岩稳定、确保抽水蓄能电站工程长安全稳定运行的一种有效技术手段[2]。
岩石裂隙灌浆技术存在隐蔽性强特点,为了使灌浆透明化,岩石灌浆数值模拟的研究于20世纪80代开始,当时主要采用有限元方法和有限分方法进行模拟[3]。随着计算机技术和数值模拟理论的不断发展,越来越多的数值方法被应用到岩石裂隙灌浆数值模拟中,如边界元法、离散元法、格子Boltzmann方法等[4]。同时,数值模拟也逐渐从二维模拟向三维模拟发展,模拟精度和模拟结果的可靠性也得到了显著提高。岩石裂隙灌浆过程可以看作是一种多相流体力学问题,涉及到岩石、水、固化剂等多种物质[5],其基本原理包括:流体运动方程、质量守恒方程、能量守恒方程、材料本构方程和界面条件等[6]。其中,有限元法和离散元法主要适用于岩石裂隙的弹性和塑性行为的分析和计算;而格子Boltzmann方法则主要适用于岩石裂隙中复杂多相流体的模拟[7]。此外,为了提高模拟的准确性和可靠性,还需要考虑到岩石裂隙的几何形状、流体的物理性质、岩石的物理性质以及固化剂的化学反应等因素[8]。岩石裂隙灌浆数值模拟是一种重要的地质工程技术研究手段[9-12],可以为工程实践提供重要的支撑和参考[13]。随着计算机技术和数值模拟理论的不断发展,岩石裂隙灌浆数值模拟将更加精细化和可靠化[14-15]。
考虑到阳江抽水蓄能电站工程(以下简称阳蓄电站)下平洞水道承受静水压力近800 m,根据《水工隧洞设计规范》(SL 279-2016),设计灌浆压力应为1~2倍的内水压力,灌浆压力和施工均超出现有工程经验,同时该工程地质条件复杂,涉及Ⅰ、Ⅱ、Ⅲ、Ⅳ(含断层带)类围岩,设计利用已有地质探洞开展了一系列科研试验工作,并通过现场高压固结灌浆试验选定了灌浆参数,取得了较好的灌浆效果,但现场试验周长、成本高。本研究利用数值仿真技术,通过建立隧洞围岩高压固结灌浆三维数值模型,开展灌浆过程数值模拟研究,分析不同围岩裂隙分布及灌浆参数对灌浆效果的影响,可减少现场灌浆试验工程量,以为今后类似灌浆工程设计提供参考。
2 工程概况
阳蓄电站位于广东省阳春市与电白县交界处的八甲山区,总装机容量2400 MW。输水系统下平洞和岔管段静水压力达799 m,最大动水压力1108 m,PD值5993 m2,属高水头大容量抽水蓄能电站,远高于国内已建的其他抽水蓄能电站,在国际上也处于前列。下平洞和岔管采用钢筋混凝土衬砌,需充分利用围岩承担内水压力,对工程地质条件要求很高。
根据勘察资料,阳蓄高压隧洞通过的岩性均为燕山三中粗粒花岗岩,除局部围岩受断层影响呈强~弱风化,其余大部分洞段深埋于微风化~新鲜的岩体内。可研阶段Ⅰ~Ⅱ类围岩约占75,断层影响带约占25(为Ⅲ类围岩,夹少量Ⅳ类围岩)。开挖阶段表明高压隧洞围岩只有少数断层破碎带(4)为Ⅲ~Ⅳ类围岩,其余均为Ⅰ~Ⅱ类岩体,岩体质量较好。
阳蓄电站引水隧洞典型断面如图1所示,钢筋混凝土衬砌内径7.5 m,衬砌厚度800 mm,开挖断面为马蹄形底宽6.0 m,高9.1 m。根据类似工程经验和现场灌浆试验,下平洞III类围岩先进行普通水泥灌浆,水泥灌浆完成后,原孔扫孔进行化学灌浆。水泥灌浆参数为:每排12孔,排距2.0 m,孔深6.0 m,分两段灌浆(第1段段长2 m,灌浆压力4.5 MPa,卡塞混凝土中;第2段段长4 m,灌浆压力10 MPa,卡塞入岩2.0 m)。本次灌浆模拟主要针对Ⅳ类围岩水泥灌浆,忽略灌浆压力对混凝土衬砌的影响,按全孔一次性灌浆处理。

图1 阳蓄高压隧洞横断面图Fig.1 Cross-sectional and longitudinal profile of the high-pressure tunnel test section in the Yang-Xu tunnel
3 复杂裂隙网络灌浆模型
3.1 三维随机裂隙网络建模蒙特卡罗方法用于随机裂隙与孔隙建模成为数值模型构建的常规手段,该方法首先建立一个概率模型或随机过程,然后通过对模型或过程的观察或抽样试验来计算所求参数的统计特征,最后给出所求解的近似值。针对阳蓄电站下平洞II类、III类、Ⅳ类围岩裂隙分布情况(Ⅳ类围岩裂隙分布参数见表1),用蒙特卡罗方法分别对上述调查获取的裂隙数据(位置、产状、尺寸、张开度)进行随机模拟,可以生成不同围岩类别下三维随机裂隙网络。研究采用COMSOL软件中的Matlab接口进行编程,利用Matlab中丰富的函数库资源和强大的计算能力快速生成多组不同产状、尺寸、张开度和数量的裂隙。灌浆孔孔径50 mm、孔深6 m。通过建立隧洞模型,并引入灌浆孔和裂隙网络,可以获得阳蓄隧洞围岩三维随机裂隙网络灌浆模型。将灌浆孔和隧洞的几何模型与建立的三维随机裂隙网络求并集,获得包含裂隙网络、灌浆孔和隧洞的几何模型;然后通过集运算,将隧洞和灌浆孔内部区域掏空,最终获得阳蓄隧洞围岩三维随机裂隙网络灌浆模型,三维随机裂隙网如图2所示。计算模型采用以隧洞为中心直径30 m的圆柱体,即围岩厚度取为洞径的3倍多。

表1 Ⅳ类围岩裂隙分布参数

图2 三维随机裂隙网络灌浆模型Fig.2 Three-dimensional stochastic fracture network grouting model
3.2 浆液的流变方程灌浆浆液是一种特殊的流体,而被灌裂隙网络是一种特殊的流体通道。在建立含复杂裂隙网络岩体灌浆系统理论前,需要首先了解浆液的流变特性。对于水泥浆液流型的判定,浆液的水灰比存在一定的关系。阮文军[16]通过试验研究认为,纯水泥浆液根据水灰比的不同可划分为3种流型:牛顿型(水灰比为2.0~10)、宾汉姆型(水灰比为0.8~1.0)和幂律型(水灰比为0.5~0.7)。罗平平等[17]认为水灰比大于1.0的水泥浆属于牛顿型,水灰比小于1.0的水泥浆属于宾汉姆型。基于有限单元法开发的COMSOL 软件的稀物质传递模块,对水泥浆液在阳蓄隧洞围岩复杂裂隙网络内的渗透扩散过程进行模拟。为了简化计算,做出如下假设:①浆液在扩散过程中不发生化学反应,即COMSOL中稀物质传递模块的稀物质反应速率为0;②灌浆为全孔段灌浆,且浆液初始压力水头处处相等,为灌浆泵输出压力﹔③灌浆模拟压力达不到地层劈裂条件。COMSOL软件中的稀物质传递模块采用基于Fick扩散定律的物质对流扩散微分方程式:
(1)
式中:D为物质的扩散系数;H为物质的浓度;Re为物质的反应速率。其中,D=Ke/S,H=P/γ,S=ρg(α+nβ)。当式(1)中物质的反应速率Re为0时,它与流体渗流运动微分方程是等价的,故可以利用该模块来分析灌浆浆液的渗透扩散规律。
3.3 计算条件和参数裂隙饱和渗透系数根据立方定律估计,不考虑岩体孔隙的渗透性。灌浆孔内壁设置为压力入口边界,压力值等于灌浆压力,模型外边界及隧洞内壁设置为零压力边界(地下水主要是储藏于断层及裂隙密集带中的脉状裂隙水,大部分洞段干燥无水)全域压力值为0,灌浆时间取120 min。多孔介质中贮水系数为0.25,由于裂隙的贮水能力远弱于孔隙介质,取为0.025。模型围岩参数为典型的花岗岩,取花岗岩常规参数。通过比重瓶法[18],获得普通硅酸盐水泥的密度为ρco=3.0 g/cm3,超细水泥的密度为ρcs=3.1 g/cm3。通过试验,水灰比W/C与水泥浆液固体颗粒的体积分数ω的关系如下:
(2)
式中:ω为体积分数;W为水的质量;C为水泥质量;ρ为密度。
浆液的黏度为浓度的函数,不考虑其随时间的变化,查阅类似工程的灌浆数据[19],可以得到如下关系式:

(3)
式中μg为黏度。不同水灰比浆液的体积分数和黏度见表2所示。

表2 不同水灰比浆液的体积分数和黏度
3.4 模拟工况为了优化计算,对阳蓄下平洞围岩灌浆数值模拟做出如下假设,忽略止浆塞对浆液渗透扩散的影响,假设浆液充满整个灌浆钻孔后才开始向四周进行扩散;浆液在扩散过程中是以不可压缩流体形态而存在,且不会发生化学反应,即Re=0;灌浆钻孔中的初始浆液压头处处相等,且保持为灌浆泵提供的灌浆压力;对不同的浆液水灰比(3、2、1、0.8)、灌浆压力(10、8、6、4 MPa)的工况进行敏感性分析。
4 浆液扩散示踪验证
浆液锋面的位置随时间的推进不断变化,它决定了浆液在裂隙网络内的扩散范围,其模拟的合理性关系着模拟结果的可靠性和精度。目前处理自由锋面问题的方法有MAC法、VOF法、水平集法和相场法等[20-21]。为了验证COMSOL中的稀物质传递模块能够示踪浆液锋面的变化,以下将对流扩散方程法与相场法、水平集法进行对比[22]。示踪模型分两部分,下矩形为流体一(浆液),设长0.3 mm,宽0.15 mm;上矩形为流体二(水),设宽度为0.15 mm,高度为0.5 mm。取长0.65 mm、宽0.3 mm的水平裂隙进行模拟,裂隙开度为0.15 mm,浆液黏度为8.2×10-3Pa·s,灌浆压力为0.2 MPa,灌浆时间为1×10-3s,分别采用相场法和对流扩散方程法、水平集法标记浆液在该水平裂隙内的扩散范围,并进行对比,结果如图3所示。从这三组不同时刻浆液的扩散范围对比图可以看出,采用对流扩散方程法可以得到与相场法、水平集法相同或相近的结果,说明该方法可以用于本工程灌浆数值模拟。
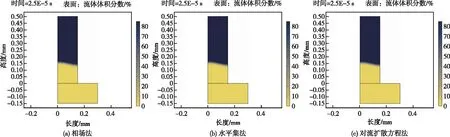
图3 不同方法浆液锋面示踪Fig.3 Tracing the front of mucus using different methods
5 结果分析
5.1 灌浆时间的影响为了选取典型的压力和浆液水灰比进行分析,在图4中显示了10 MPa灌浆压力下水灰比为0.8的浆液灌浆时间为120 min时的扩散范围云图。从图中可以看出,灌浆时间对浆液扩散范围和渗透速度有着明显的影响。当灌浆时间为5 min时,流体体积分数占到50的扩散面积相对较小,浆液只扩散了钻孔穿过的裂隙,并且水泥颗粒的扩散范围刚开始侵入裂隙面内。这表明在灌浆初,裂隙内的浆液水泥颗粒开始慢慢渗透扩散,而且扩散范围主要局限于钻孔附近。当灌浆时间增加到30 min时,流体体积分数占到50的范围进一步扩大,表明浆液水泥颗粒开始沿着单一裂隙面逐渐运移扩散。此时,裂隙内的浆液已经开始覆盖更大的面积,并且在裂隙内的扩散成为主要的运移方式。当灌浆时间到达60 min时,部分裂隙面已经扩散充填完整,部分裂隙流体体积分数50的范围已经饱和,开始渗透到其他交叉裂隙面。这表明,随着时间的推移,浆液开始逐渐充填并覆盖整个裂隙系统,甚至扩散到其他贯通的裂隙中。同时,上部围岩中的裂隙面也开始逐渐被浆液所充填。当灌浆时间增加到120 min时,扩散范围更大,水泥颗粒开始渗透到其他贯通裂隙,此时贯通裂隙的扩散面流体体积分数较小,扩散距离达10 m。表明在灌浆的后,浆液已经扩散充填了整个裂隙网络,并扩散到了较远的裂隙中,从而形成了一个完整的浆体充填层。

图4 10 MPa灌浆压力下水灰比0.8的浆液的扩散范围Fig.4 The diffusion range of a slurry with a water to solid ratio of 0.8 under a grouting pressure of 10 MPa
综上所述,当灌浆时间较短时,浆液只能充填钻孔穿过的裂隙,扩散面积较小;而随着灌浆时间的增加,浆液逐渐渗透到裂隙内部并沿着裂隙面向外扩散,扩散面积逐渐增大。当灌浆时间达到一定程度时,裂隙内的水泥颗粒也会逐渐饱和,无法再继续扩散运移。因此,在灌浆过程中,需要逐步提高灌浆压力,以保证浆液充分渗透到裂隙内部,并尽可能地填充裂隙,从而达到良好的加固效果。
5.2 灌浆压力的影响图5为10 MPa压力下水灰比0.8的浆液压力影响范围云图。从图中可以看出,当灌浆时间为5 min时,压力分布主要集中在灌浆孔可以穿过的裂隙处。这是因为在短时间内,浆液只能在较小的空隙中流动,而且在灌浆孔附近形成了一个相对稳定的压力区域。这个稳定区域的大小和形状取决于岩石裂隙的尺寸和形态,以及灌浆孔的位置和大小等因素。当灌浆时间增加到30 min时,压力开始在部分裂隙处增大。这是因为随着时间的推移,浆液逐渐填充了更多的裂隙,并且在裂隙中形成了更大的压力。但是,压力的分布范围没有扩大,这表明注入的浆液已经充分填充了所有可以穿过的裂隙。此外,压力分布图中的颜色也变得更加深色,表明在这些区域中压力更大。随着灌浆时间的继续增加,压力分布范围没有进一步扩大。原因分析,在灌浆孔周围形成了一个比较稳定的压力区域,浆液在该区域停留的时间更长,从而增加了压力。研究结果表明,在10 MPa压力下,水灰比为0.8的浆液灌浆时,随着灌浆时间的增加,浆液逐渐填充了更多的空隙,并在部分裂隙中形成了更大的压力。在灌浆孔周围,由于浆液的注入,形成了一个较高的压力区域,这个区域可以扩散到一些裂隙中,从而使这些裂隙中的压力增加。但是,如果这些裂隙本身较小,那么浆液注入后会很快充填完毕,随后的时间里,压力的分布范围就不会继续扩大。此外,研究还可以考虑更多的参数,例如不同的压力、不同的浆液配比、不同的裂隙尺寸等。这些参数的变化都会对压力分布产生影响。通过进一步的研究,可以更好地理解灌浆工程中的压力分布情况,从而为工程设计提供更加可靠的依据。这里需要指出,图5只是一个定性的描述,实际上压力分布情况是比较复杂的,需要使用数学模型和计算机模拟等方法进行更加精确的分析。但是,本研究可以提供一个直观的认识,可以帮助工程设计和施工更好地理解灌浆工程中的压力分布情况,以及如何优化灌浆工艺,提高灌浆效果。

图5 10 MPa压力下水灰比0.8的浆液压力影响范围Fig.5 The pressure influence range of a slurry with a water to solid ratio of 0.8 under a pressure of 10 MPa
5.3 灌浆量的影响图6(a)—图6(d)为不同水灰比和灌浆压力下的灌浆量。从图中可以看出,4 MPa及以上压力作用下注入量非常接近,这表明水泥颗粒运移量受压力影响较小。实际上,压力是驱动浆液流动的能量,在高压能量足够的情况下,增加压力不会显著加速水泥颗粒的运移速度。此外,从图中还可以看出,随着水灰比的增加,灌浆量也增加。这是因为水灰比的增加会降低浆液的黏度,从而增加浆液的流动性,直接导致注入量的增加。在水灰比为3的情况下,浆液的黏度接近于水,因此注入量远远超过水灰比为0.8的浆液。水灰比越大注入率增长越快。在灌浆的起始阶段,灌浆量的增长率较快,从图中也可看出在前10 min时斜率较大;随着灌浆时间的延长,超过10 min时,灌浆的增长率下降,间接表明灌入量在下降。当水灰比增加时,注入率增长的速度也越来越快。最后,根据数值分析可以进一步表明,注入量和压力之间存在关系,但是水泥颗粒运移量和压力之间并没有明显的关系。当压力增加到一定程度时,对于浆液中颗粒的运移作用较小。表明,虽然增加压力可以增加注入量,但是增加压力并不能显著提高水泥颗粒的运移速度。

图6 灌浆时间120 min不同压力和水灰比浆液的灌浆量Fig.6 Grouting volume of slurry with different pressures and water to solid ratios at a grouting time of 120 minutes
6 结论
(1)灌浆起始阶段,水泥颗粒运移距离与灌浆历时呈正相关,但灌浆范围内的裂隙达到饱和后颗粒运移距离不再随时间延长而增加。当灌浆时间较短时,浆液只能充填钻孔穿过的裂隙,扩散面积较小;而随着灌浆时间的增加,浆液逐渐渗透到裂隙内部并沿着裂隙面向外扩散,扩散面积逐渐增大;当灌浆时间达到一定程度时,裂隙内的水泥颗粒也会逐渐饱和,无法再继续扩散运移。
(2)在灌浆过程中需要逐步提高压力,以保证浆液充分渗透到裂隙内部,当灌浆压力超过一定数值,水泥颗粒运移量受灌浆压力影响较小;当压力增加到一定程度时,水泥颗粒运移量和压力没有明显的关系,对于浆液中颗粒的运移作用较小;即灌浆压力的无限增大,对于增加有效驱使浆液扩散的动力无益。随着浆液水灰比的增加,灌浆量也增加;水灰比越大注入率增长越快。
(3)本文利用COMSOL多物理场耦合软件平台,采用蒙特卡洛法,结合MATLAB二次开发生成三维随机裂隙,并用相场法、水平集法对提出的对流扩散方程法进行了验证,得出的研究结果相近,该方法可为灌浆数值模拟开发和灌浆工程设计提供重要参考。
