新一代天气雷达风轮机杂波识别和剔除

摘要：针对新一代天气雷达数据存在风轮机杂波污染问题，统计分析了5种雷达基数据特征量，风轮机杂波具有较高的反射率因子隆起度（UdBT）和水平通道信噪比隆起度（USNRH），有较大的速度奇异率（SV），其信号质量指数（ISQ）接近1，谱宽（W）接近0或大于7 m·s-1。以特征量统计结果为基础，使用模糊逻辑算法对雷达基数据中的风轮机杂波进行了特征识别，结果显示，模糊逻辑算法能有效地把风轮机杂波从各种强度的气象降水回波和固定地物杂波中识别出来。针对被识别出来的风轮机杂波，使用区域平均插值方法对雷达基数据中的风轮机杂波进行剔除，杂波剔除结果显示，气象降水条件下获得了较好的风轮机杂波剔除效果。

关键词：多普勒天气雷达；风轮机杂波；杂波特征和识别；雷达数据质量控制

中图分类号：TN959.4   文献标志码：A   文章编号：2096-3599（2023）03-0001-00

DOI：10.19513/j.cnki.issn2096-3599.2023.03.006

Wind turbine clutter identification and suppression for CINRAD

SU Tianji1， GE Junxiang2

（1. Yantai Meteorological Bureau， Yantai 264003， China; 2. School of Electronics & Information Engineering， Nanjing University of Information Science & Technology， Nanjing 210044， China）

Abstract： In order to suppress the wind turbine clutter （WTC） in CINRAD， the statistical analysis of 5 characteristic quantities from radar base data is present. The WTC has higher reflectivity uplift （UdBT） and horizontal channel SNR （signal-to-noise ratio） uplift （USNRH）， bigger singular velocity （SV）， the signal quality index （SQI） is close to 1， and the spectral width （W） is close to 0 or greater than 7 m·s-1. Based on the statistical results of characteristic quantities， the fuzzy logic algorithm is used to identify the WTC from the base data. The identification results show that the WTC can be effectively identified from the meteorological precipitation echoes and the fixed ground clutter by the fuzzy logic algorithm. Then the regional average interpolation is used to suppress the identified WTC from the base data. The clutter suppression results show that the WTC suppression effect is better in the case of meteorological precipitation.

Keywords： CINRAD; wind turbine clutter （WTC）; characteristics and identification of clutter; radar data quality control

引言

目前公認的由人类驱动的全球气候变化的威胁为许多绿色能源技术的发展铺平了道路，风力发电是一个例子。根据全球风能理事会的报告[1]，全球风电装机容量保持10%以上的快速增长，而中国的风电规模是最大的，其风电总装机容量和每年新增装机容量在全世界占比均超过三分之一。虽然风电产业取得了许多积极成果，但这种扩张的负面影响也不容忽视，其中一个影响是风力涡轮机（简称“风轮机”）对天气雷达系统的干扰[2-5]。风轮机工作时转动的叶片能使雷达载波产生多普勒频移，导致雷达回波数据中出现位置固定并且具有很高径向速度的杂波，称为风轮机杂波（wind turbine clutter，WTC），目前使用的天气雷达杂波滤波器难以滤除此类杂波。风轮机杂波会影响天气雷达观测的基数据及其后续反演产品，例如雷达定量降水估计等。为降低风轮机杂波对天气雷达的影响，国外一些学者已提出一些杂波识别和抑制方法，如Hood等[6]以风轮机杂波的时域和频域特征为基础，利用模糊逻辑算法实现风轮机杂波的自动识别。Nai等[7]基于天气目标雷达回波信号的空间连续性特征，使用距离-多普勒谱和回归的处理方法，实现风轮机杂波的抑制。Uysal等[8]把天气目标信号和风轮机杂波信号分别模型化为时域稀疏群和稀疏时间导数模型来分离这两种信号，在美国下一代天气雷达进行了模拟和实测数据计算，改善了反射率因子、径向速度和速度谱宽数据的质量。Beauchamp等[9]把风轮机杂波模型化为一个广义循环平稳过程，实现了风轮机杂波与降水回波和地杂波的分离。Dutta等[10]利用广义似然比检验方法检测受风轮机杂波影响的库，然后使用信号子空间估计的方法实现风轮机杂波抑制。国内一些学者利用国外的天气雷达数据研究了风轮机杂波的识别和抑制方法，如何炜琨等[11-13]使用美国WSR-88D雷达数据，利用模糊逻辑算法实现基于多时次采集基数据的风轮机杂波识别；基于气象目标回波空间均匀的假设，改进基于最大后验概率（MAP）方法，使用未受杂波污染的气象回波对风轮机杂波污染区进行插值，实现天气雷达基数据风轮机杂波的剔除；在风轮机杂波周期特性抑制算法的基础上，使用风电场附近未受杂波污染区的IQ（In-phase & Quadrature component ）数据对基于周期特性的风轮机杂波数据进行杂波抑制。吴仁彪等[14]利用匹配追踪算法实现仿真天气雷达风轮机杂波信号的抑制。

截至2022年，中国已建成由236部多普勒天气雷达组成的世界最大的业务化天气雷达监测网，而随着中国风电工业的快速发展，风轮机杂波对多普勒天气雷达数据质量的影响也不断加重。目前，多普勒天气雷达业务运行的基于高斯模型的自适应滤波器（Gaussian model adaptive processing，GMAP）[15-16]对风轮机杂波处理效果不理想。国内很多学者研究了多普勒天气雷达固定地物杂波、超折射回波、生物回波、电磁干扰杂波等非气象回波的特征和识别、抑制方法[17-23]，但针对风轮机杂波的研究却很少。

本文使用CINRAD/SA型多普勒天气雷达基数据，根据风轮机杂波的特点，构建基数据风轮机杂波特征量，统计了各特征量的数值分布特征。利用模糊逻辑算法识别了不同天气条件下基数据中的风轮机杂波，基于气象降水回波在一定范围内均匀的假设，使用平均值插值法剔除基数据风轮机杂波。由于目前尚缺有效的多普勒天气雷达风轮机杂波的抑制方法，本研究结果可望对进一步提高多普勒天气雷达的数据质量提供参考。

1 数据和方法

业务运行的CINRAD/SA型新一代多普勒天气雷达采用体扫描模式进行数据采集，常用的VCP21体扫模式约每6 min完成一次扫描，探测数据以标准格式保存到基数据文件中。基数据中包含反射率因子、径向速度、谱宽、信号质量指数、水平通道信噪比等数据类型，双偏振雷达还包含差分反射率、相关系数、差分传播相移率、垂直通道信噪比等数据类型[24-26]。基数据代表的最小目标单元是距离库，一个距离库是一个波束宽度（约1°）和一个脉冲有效照射深度（如250 m）所围成的空间体。烟台CINRAD/SA型新一代多普勒天气雷达（简称“烟台雷达”）基数据除了受到周围高山引起的固定地物杂波污染外，还受到风轮机杂波污染，以雷达为中心的100 km半径范围内，有20处风电场对雷达有影响。本文选用烟台雷达的基数据进行风轮机杂波特征分析、识别和杂波数据剔除，进行特征分析的不同目标类型数据包括风轮机杂波、固定地物杂波和降水回波。3类数据的获取方法是：首先利用卫星地图获得20处风电场和3座高山的区域边界数据，然后转换成雷达的方位距离信息，并在雷达软件中记录，依据定位信息可从基数据中获得风轮机杂波数据和固定地物杂波数据，降水数据则从完全避开任何杂波污染的位置获取。

1.1 模糊逻辑算法

模糊逻辑算法把只取 0 和 1 二值的普通逻辑集合概念推广到在[0，1]区间上可连续取值的模糊集合，并使用“隶属度”概念来精确描述元素与模糊集合之间的包含关系。算法包括四个过程：模糊化、规则推断、权重集成和退模糊，即依据量化特征设置隶属度函数，然后进行逻辑推理和隶属度输出加权，最后进行逻辑归类实现解模糊输出。模糊逻辑算法应用广泛，在天气雷达回波分类、降水相态识别、杂波识别等方面均有应用[27-29]。特征量对模糊逻辑算法至关重要，风轮机杂波既具有固定地物杂波的特点，其位置固定，反射率因子很大，又具有气象降水回波的特点，有一定的径向速度，信号质量指数高，因此，用于风轮机杂波特征识别的特征量，必须既能分辨气象降水回波与风轮机杂波，又能分辨固定地物杂波与风轮机杂波。

1.2 雷达基数据特征量

根据风轮机杂波的特点，构建反射率因子隆起度（UdBT）、速度奇异率（SV）、水平通道信噪比隆起度（USNRH）、信号质量指数（ISQ）和谱宽（W）等5个特征量。这5个特征量中， UdBT、SV和USNRH是利用基数据反演的特征量，反映了目标距離库与其周围距离库基数据的差异程度。而ISQ和W是直接来自基数据的特征量，反映的是目标距离库的数据特征。

1.2.1 反射率因子隆起度（UdBT）和水平通道信噪比隆起度（USNRH）

风轮机杂波的反射率因子值很大，并且区域不均匀，构建的反射率因子隆起度（UdBT）要能反映目标距离库反射率因子的这种特点，因此构建式（1）计算得到UdBT：

（1）

式中，dBT表示目标距离库的反射率因子；dBTa，r表示以目标距离库为中心，方位和距离分别变化a和r个最小分辨单元的距离库的反射率因子，当a和r同时为0时即为dBT；Nbin表示dBTa，r对应的所有距离库数目，其大小由n和m确定。表示目标距离库的外围距离库反射率因子的平均值，由式（2）计算得到：

（2）

式中，为外围距离库中的最大反射率因子值，计算时剔除的目的是降低孤立极大值对平均值的影响。当dBT小于或等于时，UdBT直接赋0值，即只考虑数据的区域隆起而不考虑凹陷，因为只有风轮机杂波反射率因子大于周围晴空回波或降水回波时，才会产生不利影响。UdBT的单位是dBZ。

风轮机杂波的水平通道信噪比具有与反射率因子相似的特征，因此，将式（1）和式（2）中的dBT换成SNRH，即可计算水平通道信噪比隆起度（USNRH），USNRH的单位是dB。

1.2.2 速度奇异率（SV）

风轮机杂波的径向速度在区域内是不均匀的，速度奇异率要能反映这种不均匀特征，SV由式（3）计算得到：

（3）

式中，V表示目标距离库的径向速度，Vr表示以目标距离库为中心，距离变化r个最小分辨单元的距离库的径向速度，当r为0时即为V。k根据V与Vr的符号差异取不同值，当V与Vr异号时，k取5，否则k取10。k如此取值的依据是当参与比对的两个径向速度值为异号时，其差值的绝对值超过5 m·s-1即认为奇异度较高，而同号时其差值的绝对值超过10 m·s-1才认为奇异度较高。SV的单位是m·s-1。

速度奇异率SV可以表征V在区域内的奇异程度。当目标区域为大范围气象降水回波时，V的连续性好，SV将接近于0；而当目标为高山时，由于地表树木随风摆动，会产生一定的径向速度，SV大于0；当目标为风轮机时，受风向的影响，雷达波束与风车叶片的转动平面有不同的夹角，产生的径向速度取决于环境风向和风速、风轮机与雷达的相对位置以及风轮机叶片长度，距离库间的径向速度差异会比较大，导致SV也很大。因此，当目标为有植被的高山和风轮机时，径向速度的方向多变，所以相对于气象降水的SV，这两种目标物的SV值会较大。在气象回波的速度突变区域，如速度模糊和风切变边界等，虽然也存在速度大小和方向的突变，但目标距离库的径向速度在突变前或突变后的区域内是均匀的，因此，速度模糊区域的速度奇异率依然比风轮机杂波的小。

1.2.3 信号质量指数（ISQ）

ISQ表示在目标距离库内相邻两次脉冲采样回波信号的相似程度。在新一代天气雷达业务运行的扫描策略中，最小脉冲重复频率（pulse repetition frequency，PRF）通常为322 Hz，对应采样间隔PRT（pulse repetition time；PRT=1/ PRF）约为3 ms，一个采样周期发射28个采样脉冲用时约84 ms。在一个采样周期内，风轮机叶片受环境风驱动做匀速圆周运动，一个PRT内叶片转动约0.3°[30-32]，由于运动速度的大小和方向都不会发生明显变化，因此一个含风轮机距离库有接近于1的ISQ值。对于气象回波，虽然也可以有很高的取值，但因为其弥散目标特性，各散射体间有相对运动，导致ISQ接近于1的比例要低得多。而固定地物杂波，因为受其表面植被和空气湍流等影响，ISQ值比前两种目标明显更低。

1.2.4 谱宽（W）

谱宽表示目标距离库内所有散射体径向速度的离散程度。考虑波束展宽，距离雷达80 km处的一个目标距离库在雷达方位上展宽到约1 396 m（2πR/360）。当一个距离库内只存在一个风轮机时，雷达回波主要由风轮机产生，则多个脉冲对目标距离库进行持续采样后，其径向速度的一致性会很高，因此谱宽会很小。但当目标距离库内存在多个风轮机或有其他不同类型的目标物时，即使环境风向一致，但风轮机的布局大概率受地形影响而导致产生差异很大的径向速度，从而谱宽也很大。

2 基数据特征量的统计特征

为了获得风轮机杂波区别于降水回波、固定地物杂波的特征量数值分布特征，选取烟台雷达在2019年3月21日晴空、2019年5月5日弱降水、2019年6月5日强降水、2019年4月9日大范围降水、2019年7月10日弱对流以及2019年6月4日强对流等6种典型天气条件下若干个连续体扫的基数据，提取和计算获得降水、固定地物和风轮机这三类目标回波的特征量。在各种天气条件下所选取的降水回波避开已知风电场和固定地物，确保所选的降水回波不含风轮机杂波和固定地物杂波。但是，在有降水时，一些风轮机杂波距离库和固定地物杂波距离库会混杂有降水回波。而因为风电场布设在较高处，导致风轮机杂波中可能混杂有固定地物杂波。所选择的3处高山确定没有布設风电场，所以，统计的固定地物杂波必然不包含风轮机杂波。表1为风轮机杂波、固定地物杂波和降水回波三种类型目标回波对应的5种特征量所积累的距离库数，同一目标类型的距离库，其特征量的距离库数对不同天气条件进行累积。

不同目标性质的特征量，其取值范围不同，但可能发生取值区间重叠。这里，用落在各取值区间的距离库频数分布来表征各特征量的统计特征。另外，定义一个特征量取值的“二八区间”概念，即特征量值落入二八区间内的距离库数目比例为80%，而落在二八区间外左右两边的距离库数目比例各为10%。

2.1 反射率因子隆起度统计特征

图1所示为统计的风轮机杂波、固定地物杂波和降水回波的反射率因子隆起度（UdBT）在各取值区间的距离库频数分布图。3种目标类型UdBT取值的二八区间分别为[12.8，42.8] dBZ、[30.8，49.7] dBZ和[8.1，19.6] dBZ。可见，降水回波的UdBT较其他两种目标物的值明显较小，风轮机杂波的UdBT较固定地物杂波的UdBT略小，这是因为风轮机杂波和固定地物杂波都是不均匀的强回波，而气象降水回波较均匀；但对风轮机的探测，雷达波束的充塞度一般较固定地物小。从数值上看，当UdBT＞20.0 dBZ时，风轮机杂波的分布比例为77.06%，固定地物杂波的分布比例为99.65%，气象降水回波的分布比例为9.36%。进一步提高UdBT，当UdBT＞35.0 dBZ时，则风轮机杂波的分布比例为27.49%，固定地物杂波的分布比例为75.94%，气象降水回波的分布比例为0.15%。因此，使用UdBT可从气象回波中把风轮机杂波和固定地物杂波检测出来，但风轮机杂波和固定地物杂波的UdBT特征较接近，特征值区间重叠，二者不易分辨。结合二八区间，风轮机杂波的UdBT取值区间选为[20.0，42.8） dBZ。

2.2 速度奇异率统计特征

图2所示为统计的风轮机杂波、固定地物杂波和气象降水回波的速度奇异率（SV）在各取值区间的距离库频数分布图。3种目标类型SV取值的二八区间分别为[0.15，2.59] m·s-1、[0.22，2.42] m·s-1和[0.10，0.68] m·s-1。可见，降水回波的SV比其他的小，主要集中在0 m·s-1附近，因此，使用SV可以从降水中将风轮机杂波和固定地物杂波检测出来。而虽然风轮机杂波和固定地物杂波的SV频数分布规律相似，但考虑SV＞5.00 m·s-1的情况，则风轮机杂波的分布比例为2.50%，固定地物杂波的分布比例为0.13%，气象降水回波的分布比例为0.18%。考虑到风轮机杂波中可能含有固定地物杂波和气象降水回波，因此，SV＞5.00 m·s-1可作为风轮机杂波的特征，取值区间选为[2.59，5.00） m·s-1。

2.3 水平通道信噪比隆起度统计特征

图3所示为统计的风轮机杂波、固定地物杂波和降水回波的水平通道信噪比隆起度（USNRH）在各取值区间的距离库频数分布图。3种目标类型USNRH取值的二八区间分别为[7.3，29.4] dB、[12.5，27.3] dB和[9.2，24.9] dB。可以看出，三者分布特征较接近。仍然考虑到风轮机杂波中可能含有固定地物杂波和气象降水回波的情况，当USNRH＞30.0 dB时，风轮机杂波的分布比例为9.3%，固定地物杂波的分布比例为5.8%，气象降水回波的分布比例为3.0%。进一步提高USNRH，当USNRH＞40.0 dB时，则风轮机杂波的分布比例为2.1%，固定地物杂波的分布比例为0.6%，气象降水回波的分布比例为0.2%。因此，USNRH＞40.0 dB可作为风轮机杂波的特征，其取值区间选为[29.4，40.0） dB。

2.4 谱宽统计特征

图4所示为统计的风轮机杂波、固定地物杂波和降水回波的谱宽（W）在各取值区间的距离库频数分布图。3种目标类型W取值的二八区间分别为[0，5.0] m·s-1、[1.0，4.5] m·s-1和[0.5，4.5] m·s-1，区别不大。但是，W是单距离库特征量，如前所述，风轮机杂波的谱宽可能趋向于0 m·s-1，也可能很大。当W＜0.5 m·s-1时，则风轮机杂波的分布比例为26.33%，固定地物杂波的分布比例为5.30%，气象降水回波的分布比例为7.18%；当W＞7.0 m·s-1时，则风轮机杂波的分布比例为2.51%，固定地物杂波的分布比例为0.16%，气象降水回波的分布比例为0.52%。因此，W趋于0 m·s-1或大于7.0 m·s-1可作为风轮机杂波的特征，取值区间为[0，0.5]∪[7.0，+∞） m·s-1。

2.5 信号质量指数统计特征

图5所示为统计的风轮机杂波、固定地物杂波和降水回波的信号质量指数（ISQ）在各取值区间的距离库频数分布图。3种目标类型ISQ取值的二八区间分别为[0.28，1.00]、[0.28，0.89]和[0.33，0.95]。由图可见，风轮机杂波的ISQ主要集中于1附近。当ISQ＞0.98时，则风轮机杂波的分布比例为25.0%，固定地物杂波的分布比例为4.8%，气象降水回波的分布比例为5.4%。因此，ISQ＞0.98可作为风轮机杂波的特征，对应的取值区间为[0.98，1.00）。

3基数据风轮机杂波识别

利用雷达基数据风轮机杂波的统计特征，使用模糊逻辑算法对基数据的风轮机杂波进行识别。

3.1 风轮机杂波隶属度函数

隶属度主要体现风轮机杂波的属性特征，以特征量的取值判断目标距离库回波为风轮机杂波的可能性大小，隶属度0表示肯定不属于，隶属度1表示肯定属于，隶属度的取值区间为[0，1]，即为隶属度函数的值域区间。图6为依据各特征量的统计特征设计的基数据风轮机杂波5个特征量的隶属度函数，隶属度函数自变量区间直接由各特征量的统计特征决定。

3.2 风轮机杂波识别的模糊逻辑实现

输入雷达基数据，提取dBT、V、SNRH、W和SQI等5类数据，分别生成UdBT、SV、USNRH、W和ISQ等5种特征量，作為各自隶属度函数的自变量输入。目标距离库各个特征量经过隶属度函数的计算，分别输出5个隶属度值。给这5个隶属度值分配合适的权重，经过隶属度加权计算后输出的数值即为风轮机杂波的识别指数。结合已知风电场的位置，选择合适的识别指数值作为风轮机杂波的判断指标，实现输出结果的解模糊。

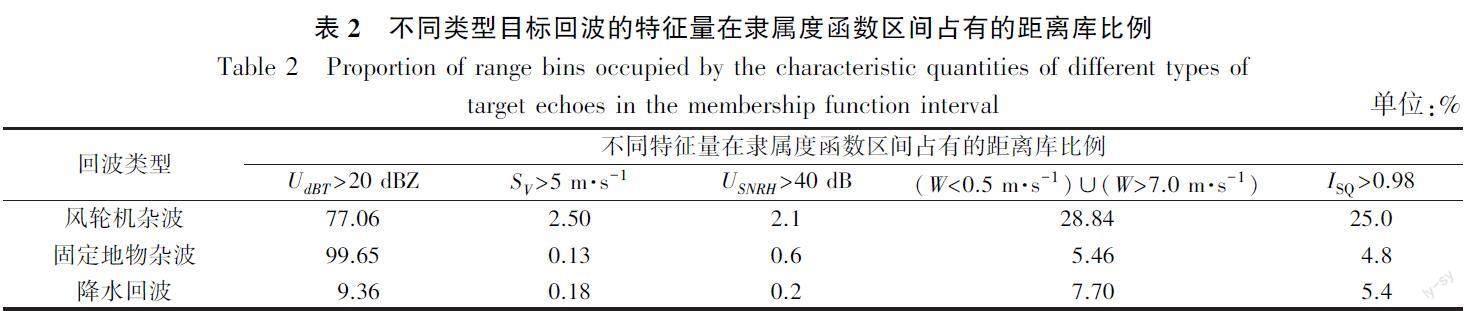
在模糊逻辑计算中，权重的分配影响重大，合适的权重有利于特征的显现。这里从风轮机杂波特征量与其他目标的特征量的差异程度来考虑权重分配，表2列出由特征量统计特征决定的隶属度函数区间分布。选择隶属度函数区间的原则是能把风轮机杂波与其他类型目标回波区分开来。

综合考虑风轮机杂波各特征量落入所选的隶属度函数区间内的距离库的绝对比例，以及与其他类型目标同一特征量落入对应隶属度函数区间内的距离库的相对比例，以此决定风轮机杂波的各特征量的权重分配。由表2可见，风轮机杂波W和ISQ的特征与其他目标对比最突出，因为绝对比例较高且相对比例较大；SV和USNRH次之，其相对比例较大但绝对比例较小；UdBT最差，其绝对比例和相对比例与固定地物杂波接近。因此，给W和ISQ分配最多的权重，均为25%；给SV和USNRH分别分配20%的权重，最后给UdBT分配10%。

另外，增加了一些距离库的限制措施，以便减少计算量。一是反射率因子值小于-5 dBZ的距离库，不参与隶属度判断。二是在加权时，同一距离库的5种特征量，隶属度为0的特征量数多于1个时，加权结果乘以一个衰减因子，即要求风轮机杂波的各项特征表现均衡。

3.3 识别结果

为了检验对不同天气条件下采集的基数据风轮机杂波识别算法的有效性，分别选取2020年2月14日晴间小阵雨、2019年10月10日弱降水、2019年7月31日强对流和2019年8月11日大范围降水等4种不同天气条件下烟台雷达采集的基数据。

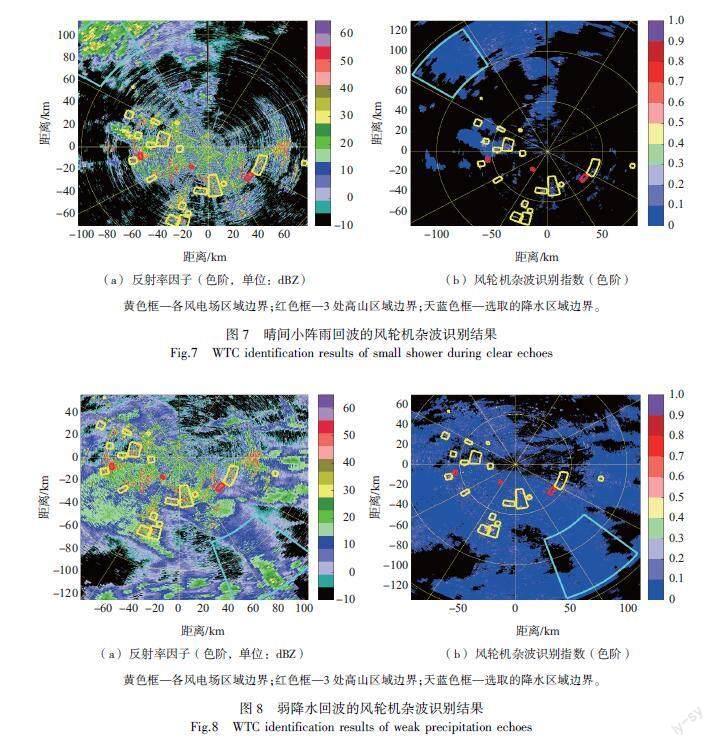
图7—10显示了所选取的4种不同天气条件下采集的基数据，对其风轮机杂波的识别结果。图7a、8a、9a、10a均为未进行地物杂波滤除的反射率因子图，图7b、8b、9b、10b均为风轮机杂波识别指数图，指数取值范围[0，1]，指数越大，风轮机杂波的可能性越大。

为了定量化描述风轮机杂波识别的准确性，取风轮机杂波识别指数不小于0.5作为标准，在识别指数符合标准的所有距离库中，定义落入风电场区域的比例为风轮机杂波识别命中率，落入3处高山区域和选取的降水区域的比例分别为固定地物误识别率和降水误识别率。选取的降水区域分别包含了速度模糊边界、风切变边界等径向速度突变边界，并且区域面积均大于风电场区域总面积，如图11所示。

黄色框—各风电场区域边界；红色框—3处高山区域边界；天蓝色框—选取的降水区域边界。

由图7—10和表3可见，4种天气条件下，风电场区域的风轮机杂波识别指数均高于其他区域，被识别为风轮机杂波的距离库有50%左右落入了事先确认过的风电场区域。降水回波区域对应的风轮机杂波识别指数很低，包括强对流降水回波，选取的包含径向速度突变边界区域的降水误识别率低于2%。3处标注的高山强回波，其风轮机杂波识别指数也很低，高山区域固定地物误识别率也低于2%。因此，设置合适的风轮机杂波识别指数阈值，可以把识别指数超过阈值的距离库回波识别为风轮机杂波，从而实现解模糊输出识别结果。对于风电场区域外存在较多风轮机杂波识别指数超过标准的情况，主要原因是雷达附近新建设了未被标注的风电场，另外，高山上树木随风摆动产生了类似风轮机的杂波。而风电场区域内，有的距离库虽然反射率因子很大，但未被识别为风轮机杂波，原因是风电场区域内多为高山，而风轮机不可能布满所有区域，并且遇到环境风速超过风轮机工作的额定风速时，风轮机会停止工作，这时，反射率因子很大的距离库均为固定地物杂波，这从另一个侧面也证明了算法的固定地物误识别率很低。

风轮机杂波识别算法构建特征量、杂波识别是在单个雷达基数据文件的基础上进行的，与文献[11]的风电场杂波检测与识别方法相比，特征量更少，构建复杂度更低，有更高的时间效率。

4 基数据风轮机杂波剔除

相对于风轮机杂波，气象降水回波是一定范围内回波强度比较均匀的回波，而晴空回波也比风轮机杂波平滑。在生成基数据前，天气雷达一般已对固定地物杂波进行滤波，很少有固定地物杂波再保存在基数据中[33-34]。因此，剔除夹杂在气象降水回波或晴空回波基数据中的风轮机杂波，可以使用平均值插值的方法来处理。以风轮机杂波距离库为中心，取其周围一定数量的非风轮机杂波距离库回波数据，去掉突变量再取平均值，用这个平均值替换风轮机杂波距离库的回波数据值，以此达到风轮机杂波剔除的目的。

选择烟台雷达在弱降水、强对流降水、大范围降水和晴空4种不同天气条件下采集并经过固定地物杂波滤除后的基数据，在雷达全覆盖范围内计算出各距离库的风电杂波识别指数，然后进行以下步骤的操作：

（1）在风电场区域内，设定一个风轮机杂波识别指数判断阈值Th。

（2）风电场区域内各距离库的风轮机杂波识别指数分别与Th进行比对，大于或等于Th的距离库的回波被判断为风轮机杂波。该距离库的反射率因子数据记为，A代表方位，R代表距离，而小于Th的距离库回波被判断为非风轮机杂波。

（3）用表示以对应的目标距离库为中心，周围3个方位×17个距离库共51个距离库的反射率因子中，风轮机杂波识别指数小于Th的距离库的反射率因子，并取出这些反射率因子数据。

（4）取中对应风轮机杂波识别指数小于Th的距离库的反射率因子的平均值，然后用这个平均值给重新赋值，即为反射率因子的区域平均值插值，以此达到剔除风轮机杂波的目的。图12—15给出了4种天气条件的反射率因子剔除风轮机杂波前后的对比图。

图12a、13a、14a、15 a为雷达业务运行中保存的不同强度和范围的气象降水回波反射率因子图，它们均预先经过了固定地物杂波滤除，其中红色框内为风电场区域，其回波强度较大的距离库存在风轮机杂波污染。图12b、13b、14b、15b为使用区域平均值插值方法剔除风轮机杂波后的反射率因子。可见，风电场区域内的风轮机杂波被较有效地剔除，并且气象降水回波基本未受影响。气象降水反射率因子的风轮机杂波剔除效果较好。图15a为晴空回波经过固定地物杂波滤除后的反射率因子，风电场区域内回波强度较大的距离库存在风轮机杂波污染。图15b为使用区域平均值插值方法剔除风轮机杂波后的反射率因子。可见，风电场区域内的风轮机杂波强度被削弱，但其剔除效果没有气象降水的好。根据调查，有气象降水时，风电场将关闭部分风轮机，而天气晴好时可用的风轮机将全部开启。因此，有气象降水时的风轮机杂波面积一般比晴空时的小，导致用区域平均值插值剔除风轮机杂波时，晴空时的效果不如有气象降水时的效果。

5 结论与讨论

（1）以CINRAD/SA型多普勒天气雷达基数据风轮机杂波的统计特征为基础，利用模糊逻辑算法对基数据风轮机杂波进行识别，并在风电场区域使用区域平均插值法实现基数据风轮机杂波的剔除。剔除效果显示，有气象降水时的风轮机杂波面积较小，杂波剔除效果较好，晴空时处理效果不如有气象降水时。该杂波剔除算法只需要单个基数据的输入，数据处理算法较简单，杂波识别和剔除时间效率更高。

（2）关于反射率因子的使用，在风轮机杂波特征量统计和杂波识别过程中，使用的是滤波前反射率因子（dBT）数据，但是在杂波剔除应用时，是在滤波后反射率因子（dBZ）上进行的，主要原因是风轮机杂波的滤波后反射率因子隆起度（UdBT）与其他两种目标物UdBZ的区别比之UdBT更不明显。考虑到风轮机杂波具有位置固定的特征，而基数据的后端应用使用的是滤波后反射率因子，因此使用UdBT进行风轮机杂波识别，然后在滤波后反射率因子上进行杂波剔除。

（3）由于风电场区域外存在较多风轮机杂波识别指数超过了设定的标准，虽然其中可能存在部分未被确认的新建风电场，但是，为了尽量减少风轮机杂波剔除处理可能对气象降水回波产生不利影响，只在风电场区域进行风轮机杂波剔除。

目前，新一代天气雷达正在进行大规模的双偏振升级[35]，风轮机杂波的双偏振参量特征是值得研究的方向。后续需要开发能适用于所有数据类型的基数据风轮机杂波剔除机制，为多普勒天气雷达數据质量的持续提高提供支撑。

参考文献：

[1] Global Wind Energy Council. Global wind report 2022 [R/OL]. [2022-10-11].https：//gwec.net/global-wind-report-2022/.

[2] ISOM B M，PALMER R D， SECREST G S， et al. Detailed observations of wind turbine clutter with scanning weather radars[J].J Atmos Oceanic Technol，2009，26（5）：894-910.

[3] NORIN L. A quantitative analysis of the impact of wind turbines on operational Doppler weather radar data[J]. Atmos Meas Tech，2015，8（2）：593-609.

[4] KARABAYIR O， COSKUN A F， YUCEDAG O M， et al. Investigation of wind farm effects on radar multiple target tracking[J].J Electromagnet Wave，2016， 30（2）：232-250.

[5] 何炜琨，吴仁彪，王晓亮，等.风电场对雷达设备的影响评估与干扰抑制技术研究现状与展望[J].电子与信息学报，2017，39（7）：1748-1758.

[6] HOOD K，TORRES S，PALMER R.Automatic detection of wind turbine clutter for weather radars[J]. J Atmos Oceanic Technol，2010，27（11）：1868-1880.

[7] NAI F， TORRES S， PALMER R. On the mitigation of wind turbine clutter for weather radars using range-Doppler spectral processing[J]. IET Radar Sonar Navig，2013，7（2）：178–190.

[8] UYSAL F， SELESNICK I，ISOM B M. Mitigation of Wind Turbine Clutter for Weather Radar by Signal Separation[J].IEEE Trans Geosci Remote Sens，2016，54（5）：2925-2934.

[9] BEAUCHAMP R M，CHANDRASEKAR V.Suppressing wind turbine signatures in weather radar observations[J].IEEE Trans Geosci Remote Sens，2017，55（5）：2546-2562.

[10] DUTTA A，CHANDRASEKAR V，RUZANSKI E. A signal sub-space based approach for mitigating wind turbine clutter in fast scanning weather radar[C]//2021 United States National Committee of URSI National Radio Science Meeting （USNC-URSI NRSM）. Boulder： Institute of Electrical and Electronics Engineers，2021：202-203.

[11] 何炜琨，郭双双，王晓亮，等.基于Level-II数据和模糊逻辑推理的气象雷达风电场杂波检测与识别方法[J].电子与信息学报，2016，38（12）：3252-3260.

[12] 何炜琨，高丽，王晓亮，等.基于改进MAP方法的气象雷达风电场杂波抑制[J].系统工程与电子技术，2018，40（5）：1018-1025.

[13] 何炜琨，高丽，王晓亮.基于一次回波数据的气象雷达风轮机杂波抑制[J].中国民航大学学报，2019，37（2）：17-22.

[14] 吴仁彪，丁红，何炜琨，等.气象雷达风电场杂波抑制的匹配追踪算法[J].信号处理，2018，34（12）：1405-1414.

[15] 孙召平，张持岸，张建云．一种基于高斯模型的自适应地物杂波滤波算法[J].太赫兹科学与电子信息学报，2013，11（2）：250-259.

[16] 陈艳，李柏，何建新，等.在天气雷达信号处理器中用IQ信号消减地物杂波[J].气象科技，2015，43（4）：569-575．

[17] 马中元，朱春巧，刘熙明，等.CINRAD雷达数据质量控制方法初探[J].气象，2010，36（8）：134-141．

[18] 李丰，刘黎平，王红艳，等.S波段多普勒天气雷达非降水气象回波识别[J].应用气象学报，2012，23（2）：147-158.

[19] 张林，杨洪平.S波段WSR-88D雙偏振雷达观测非降水回波识别方法研究[J].气象，2018，44（5）：665-675．

[20] 杜言霞，于子敏，温继昌，等.基于神经网络技术的天气雷达超折射回波识别[J].气象科技，2018，46（4）：644-650.

[21] 周雪松，孟金，姚蔚.一种基于快速傅里叶变换的多普勒天气雷达弱杂波识别方法[J].海洋气象学报，2019，39（4）：43-51.

[22] 苏添记，葛俊祥，杨传凤.新一代天气雷达电磁干扰特征识别和剔除[J].现代雷达，2020，42（10）：26-31.

[23] 姚文，张晶，余清波，等.辽河三角洲湿地鸟类活动的双偏振天气雷达回波特征[J].气象，2022，48（9）：1162-1170.

[24] 龚佃利，朱君鉴，王俊，等.2020 年 6 月 1 日山东强雹暴过程双偏振雷达观测分析[J].海洋气象学报，2021，41（3）：40-51.

[25] 刁秀广.2020年5月17日和6月1日山东强冰雹风暴双极化特征分析[J]. 海洋气象学报，2021，41（1）：68-81.

[26] 刁秀广，张磊，孟宪贵，等.两次强降水风暴双偏振参量特征分析[J]. 海洋气象学报，2020，40（3）：27-36.

[27] 曹俊武，刘黎平，葛润生.模糊逻辑法在双线偏振雷达识别降水粒子相态中的研究[J].大气科学，2005，29（5）：827-836.

[28] 张秉祥，李国翠，刘黎平，等.基于模糊逻辑的冰雹天气雷达识别算法[J].应用气象学报，2014，25（4）：415-426.

[29] 文浩，张乐坚，梁海河，等.基于模糊逻辑的新一代天气雷达径向干扰回波识别算法[J].气象学报，2020，78（1）：116-127.

[30] 李滨波，段向阳. 风力发电机原理及风力发电技术[J].湖北电力，2007，31（6）：54-55.

[31] 刘巨，姚伟，文劲宇，等.大规模风电参与系统频率调整的技术展望[J].电网技术，2014，38（3）：638-646.

[32] 汤雪松，殷明慧，李冬运，等. 变速与变桨协调的风电机组平滑功率控制[J].电力系统自动化，2019，43（2）：112-120.

[33] 郑丽娜，刘畅，宿秋兰，等．2019年6月黄河口6次局地冰雹实例分析[J].海洋气象学报，2020，40（1）：79-89.

[34] 梅婵娟，张灿，许可，等．山东半岛秋季一次脉冲风暴下击暴流观测分析[J]．海洋气象学报，2020，40（2）：131-139.

[35] 杨传凤，张骞，陈庆亮，等.济南CINRAD/SA雷达双偏振升级关键技术分析[J].海洋气象学报，2019，39（4）：116-123.