基于改进蜜獾优化算法的PID参数整定
2023-12-05胡涛,蒋全
胡 涛,蒋 全
(上海理工大学 机械工程学院,上海 200093)
群智能算法是通过模拟生物运动、追捕以及觅食等社会行为而衍生的随机搜索算法,具有结构简单、鲁棒性高等优点,常用于解决高维和目标函数不可微等复杂的全局寻优问题。受各种生物行为启发,研究人员提出了多种群智能算法[1]。
PID控制的参数优化主要分为两类:一类是基于传统优化方法进行的PID参数整定,例如Zigeel-Nihcols法[2]、Cohen-Coon法[3];另一类将智能算法引入PID整定的智能优化算法,例如遗传算法、粒子群算法模糊控制。传统优化方法具有结构简单、易于掌握的优点,适用于对精度要求不高的场合。但随着产业升级的要求,该套方法难以满足对控制精度要求越来越高的产业需要,因此本文主要讨论的是智能优化算法。文献[4]以时间乘以误差绝对值积分为基础设计适应度函数,通过改进粒子群算法整定非最小相位、一阶延迟系统的PID控制器参数,获得了较好的动态特性和鲁棒性。但该方法存在平均加速度过大、超调量非零等问题。文献[5]提出了一种基于蚁狮算法的分数阶PI永磁同步电机矢量控制,其相比传统优化算法拥有更好的抗干扰能力,但该算法存在计算量以及收敛速度慢的缺点。文献[6]将粒子群与模糊控制器结合获得了新的PI速度控制方法,与传统优化算法相比该方法具有更好的动态响应,能够自适应地对模糊逻辑控制器的隶属度函数进行优化。但此分步优化方法因模糊隶属度函数参数所需满足的条件多,导致搜索空间狭窄。
通过模拟蜜獾寻找蜂巢的两种方式,文献[7]提出了一种新型元启发式智能算法-蜜獾优化算法HBA(Honey Badger Algorithm)。HBA算法包括追踪环绕挖掘与跟随已有向导两种方式,模型简单且易于实现,需要调节的参数少,具有良好的应用前景和学术价值。但是HBA算法局部开发能力较弱,并且在优化复杂问题时难以跳出局部最优。为了提高HBA的优化性能,研究人员主要从调整控制参数、更新搜索机制、引入新算子以及算法融合等方面对算法进行改进。文献[8]提出了一种将反向学习与混沌机制引入蜜獾算法的改进算法,利用反向学习算法生成相反的随机候选粒子来提高算法的随机性。
本文提出一种基于Tent映射和正态云发生器的改进蜜獾优化算法(CHBA)。选用23个通用的标准测试函数对CHBA算法性能进行验证,分别从单峰、多峰以及复合函数寻优结果与多种优化算法进行对比分析。为了验证该算法的有效性,本文对一阶时滞系统、非最小相位系统和一阶最小延迟系统的阶跃响应PID参数进行了优化对比。结果表明,在同等测试条件下,CHBA算法寻优效率和收敛精度更高,能较快跳出局部最优解,在全局搜索和局部开发能力上更为平衡。
1 基于Tent映射正态云模型的蜜獾算法
1.1 蜜獾算法基本原理
蜜獾算法是一种新型智能优化算法,该算法主要通过模拟蜜獾智能觅食行为来进行寻优,具有寻优能力强、收敛速度快等特点。蜜獾算法将蜜獾的觅食行为分为两类,一是自主延心形线随强度信息进行挖掘蜂巢;二是跟随已有向导及其强度信息到达蜂巢。两种不同行为按50%概率随机选择。
在挖掘阶段,蜜獾的动作类似于图1所示的心形,心形线运动可由式(1)表示
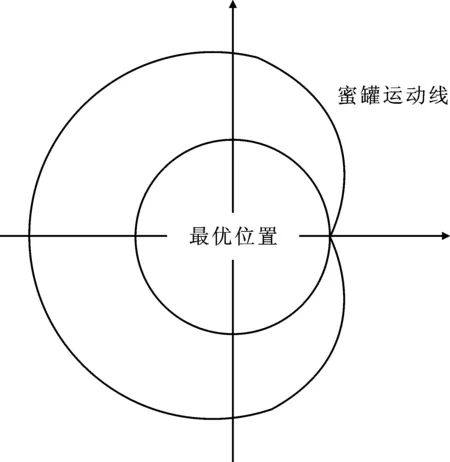
图1 蜜獾挖掘运动线Figure 1. Honey badger dig line
xnew=xprey+F×β×I×xprey+F×r1×α×di×
|cos(2πr2)×[1-cos(2πr3)]|
(1)
其中,xprey表示猎物的位置,即全局最佳位置;β≥1(默认β=6)是蜜獾获得食物的能力;di是猎物与第i只蜜獾之间的距离,见式(2);r1、r2和r3是0~1之间的3个不同随机数;F是改变搜索方向的标志,由式(2)确定
(2)
其中,r4是0~1之间的随机数。
由嗅觉强度的定义可知,强度与猎物和第i只蜜獾的距离有关。Ii是猎物的嗅觉强度,如果气味强度高,则运动快,反之亦然。Ii由图2所示的平方反比定律[9]给出,由式(3)定义。
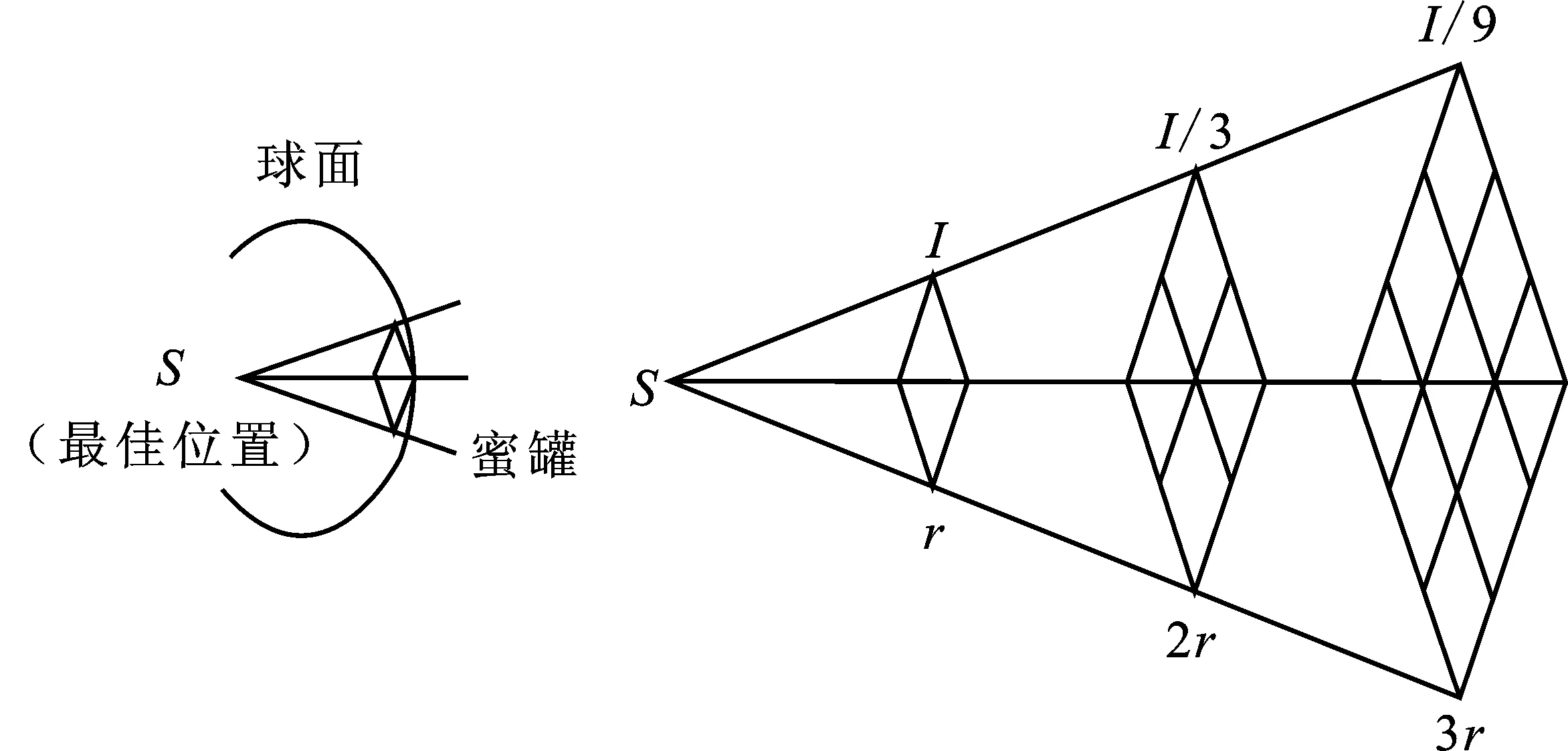
图2 蜜獾嗅觉强度Figure 2. Smell intensity of honey badger
(3)
其中,r5是0~1之间的随机数;S是源强度或浓度强度;di表示猎物和第i只獾之间的距离。
时变搜索衰减因子α表示在搜索过程中随时间变化的随机性,用于确保从勘探到开采的平稳过渡。α值随着迭代次数增加而减小,以减小随时间的随机化,如式(4)所示。
(4)
式中,C为大于等于1的常数,默认为2;tmax为迭代最大次数。
在挖掘阶段,蜜獾主要受猎物的气味强度xprey、距离di和时变搜索衰减因子α影响。此外,在挖掘活动中,由于存在干扰项F,蜜獾将在多种方向干扰的影响下向最佳位置靠拢。
蜜獾跟随蜜导鸟到达蜂巢的情况可模拟为式(5)
xnew=xprey+F×r6×α×di
(5)
其中,r6是0~1之间的随机数;xnew表示蜜獾的新位置;xprey表示猎物的位置。由式(5)可以看出,蜜獾在距离信息di的基础上,对目前发现的接近猎物的位置进行搜索。在该阶段,搜索受到时变搜索衰减因子α以及F的干扰。
1.2 引力加速蜜獾算法
引力搜索算法[10]是一种以基于粒子在空间中受其他粒子引力影响为原理设计的算法。空间中每个粒子都受到其他粒子引力的影响,并向质量更大的粒子移动,同时生成加速度。粒子质量反应为粒子的适应度值。算法中质量较小的粒子即适应度较低的粒子将逐渐接近质量较大的粒子,并最终获得最佳的适应度值,成为问题的最优解。假定有N个粒子,其质量可以定义为
mi(k)=[fi(k)-fw(k)]/[fb(k)-fw(k)]
(6)
(7)
式中,fi(k)为在第k次迭代中第i个粒子的适应度值;Mi(k)为在第k次迭代中第i个粒子的质量;fb(k)和fw(k)分别为迭代中的最佳及最差适应度函数值。
由此可得在d维空间中,粒子收到的引力为
(8)
式中,G(k)为万有引力常数;Rij(k)为粒子i与j之间的欧式距离;rj为是0~1之间的随机数。
第i个粒子的加速度可用牛顿第二定律得到,即
ai(k)=Fi(k)/Mi(k)
(9)
在蜜獾算法中,由衰减因子α对式(3)和式(5)的蜜獾位置更新进行影响,从中可以看出衰减因子α控制了蜜獾个体的搜索范围。为提高不同个体对搜索能力的需求,将衰减因子α由引力搜索算法中的加速度ai(k)替代,更新后的式(1)和式(5)为
xnew=xprey+F×β×I×xprey+F×r3×ai(k)×di×
|cos(2πr4)×[1-cos(2πr5)]|
(10)
xnew=xprey+F×r7×ai(k)×di
(11)
1.3 基于Tent映射的种群初始化
为了提高算法的优化速度和求解精度,首先要提高初始种群在搜索空间中分布的均匀性。混沌序列相比随机生成拥有更好的随机性和遍历性,并且存在规律性。混沌序列利用映射关系在(0,1)之间随机生成混沌序列,再通过对应的转换计算式转换到搜索空间内。由于Tent映射能获得更均匀分布的序列[11],因此本文将Tent映射作为初始粒子群位置的映射。Tent映射的计算式如下
(12)
式中,μ∈(0,2]为混沌参数,与混沌性成正比;i和j分别为种群数和混沌变量序号。
由于Tent映射与其他混沌映射对初值的选取均具有较高的敏感性,式(12)选用多种不同的初始值可得到其对应的混沌序列,按照对应关系转换至每个个体的搜索空间中,有
(13)
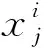
Tent映射与其他混沌映射生成初始种群及随机产生初始种群对比如图3所示。
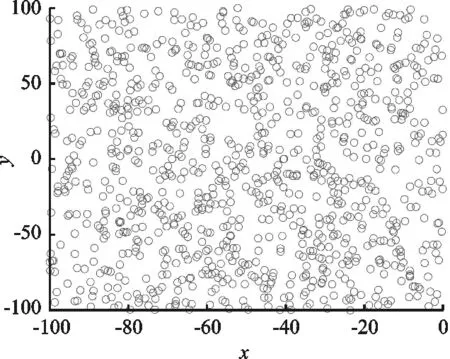
(a)
图3(a)表示由Tent映射生成的初始蜜獾种群;图3(b)表示由Sin映射生成的初始蜜獾种群;由图3(c)表示Logistics映射生成的初始蜜獾种群;图3(d)表示随机生成的初始蜜獾种群。由图3可知,在初始蜜獾种群的生成来看,使用Tent映射在空间中分布最为均匀,其次是随机生成。初始群体求解空间中分布越均匀,算法在面对不同问题时将会具有更好的寻优性能。同时使用混沌映射具有非重复性,可有效避免初始生成重复的无效个体。
1.4 正态云模型
云模型是为了能够将定量数值与定性概念间的不确定转换的概念[12],实现对数据模糊性和随意性的描述和处理。作为一种与自然界随机概率分布最符合的模型,云模型具有较重要的数学意义。
使用3个数字特征表示定性概念上的定量特征。
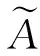
熵En:熵是期望Ex的不确定性,表现为在数域空间中能够被Ex所接受的云滴群的分布范围或模糊程度或不确定性。熵越大,在定量论域U中的分布越大,模糊性和随机性越大。
超熵He:超熵是熵En的不确定性的度量,是熵的分布范围,即熵的熵。
若UA(x)为正态分布,模型则称为正态云模型,云的数字特征如图4所示。
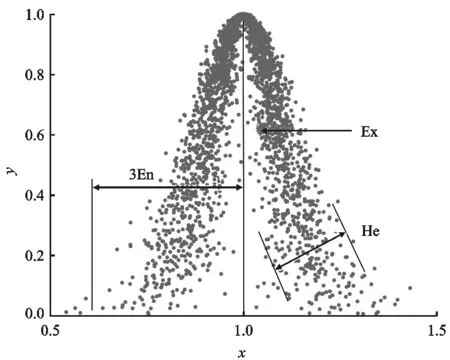
图4 正态云Figure 4. Normal cloud
为了使蜜獾算法在面对复杂优化问题时在搜索阶段的随机性更强,使算法拥有更强的跳出局部最优解能力,同时在一定程度上加强算法在开发阶段的收敛精度。将Tent映射与正态云模型映入蜜獾算法,在新算法中以迭代过程中的最佳位置为基础,将其作为正态云模型中的期望值生成第2组蜜獾。通过调节熵的取值控制新蜜獾的生成范围,通过超熵控制新蜜獾的密集程度。
在搜索过程前期,需要扩大第2批蜜獾生成范围以提高算法在开发阶段的随机性,在算法迭代后期需要降低蜜獾更新范围来提高实现算法搜索精度。为此,熵与超熵需要自适应调整,如式(14)~式(15)所示。
(14)
He=En×10-ξ
(15)
综上,改进后的算法步骤如下所示:
步骤1生成参数tmax、N、β、C;
步骤2由式(12)和式(13)采用Tent映射初始化蜜獾种群;
步骤3使用目标函数计算蜜獾个体适应度值,保存最佳位置以及适应度值;
步骤4使用式(9)更新衰减因子α;
步骤5以标准蜜獾算法更新蜜獾位置,并计算新的适应度值确定最佳位置记为X1以及其适应度值F1;
步骤6按照正态云算法以最佳位置为期望生成第2组蜜獾,并获得新蜜獾的最佳位置X2以及其适应度值F2;
步骤7将F1与F2进行对比,更新得到两组中的最佳,视为本代最佳。如果t 为了验证CHBA算法的有效性,本文选用23个国际通用的标准测试函数对CHBA进行仿真实验[8],并与多种算法例如标准HBA、SSA(Salp Swarm Algorithm)[13]、PSO(Particle Swarm Optimization)[14]、WOA(Whale Optimization Algorithm)[15]和ALO(Ant Lion Optimizer)[16]进行对比分析。为得到可信的运行结果,每种算法各独自运行30次,以标准差和平均值为基准进行对比分析[17]。其中,平均值越小,算法性能越优异;若平均值相同,则标准差越小,性能越好。统计结果采用“w/t/l”方式表示。其中,w指CHBA有w个测试函数结果明显优于其他算法,t指CHBA有t个测试函数的结果与其他算法相当,l指CHBA有l个测试函数劣于其他算法[18]。 单峰基准函数有一个全局最优解,使用单峰测试函数(F1~F7)表达式及相关参数如表1所示。由表2可见,在同等测试环境下,CHBA在全部6个测试函数下的寻优结果比其余5种算法更有优势。从F1~F4结果上的数量级差别以及F5的迭代曲线可以看出CHBA对于单峰基准函数拥有更高的寻优精度。 表1 单峰基准函数测试统计结果 表2 多峰基准函数测试的统计结果 多峰基准测试函数拥有多个局部最优解以及多个全局最优解,常用于检测算法的全局开发以及局部最优跳出能力。6个多峰测试函数(F8~F13)的表达式以及相关参数如表1所示。从表3可以看出,CHBA算法的全局探索和开发能力较标准HBA具有较大提升,其中F9~F11取得了最优值。在相同测试条件下,CHBA在全部6个测试函数下的结果同样优于其他算法,说明正态云模型所生成的第2组蜜獾提高了算法的模糊性和随机性。 表3 固定维多峰基准函数测试的统计结果 固定维多峰基准测试函数更能代表真实的工程优化问题,只有当算法的探索与开采能力更为平衡时才能保证算法不陷入局部最优解。10个多峰测试函数(F14~F23)的表达式及相关参数如表1所示,结果如表4所示。CHBA寻优性能在多数测试函数下表现优于其他算法,虽然函数F14、F15和F16下的平均值接近,但标准差略高于其他算法。改进算法具有良好的复合函数优化性能主要归因于正态云生成器中En和He的更新机制,其使算法前期具有较好的随机性和模糊性,改进了全局开发能力,后期随机性和模糊性随着迭代次数的增加而减小,有助于提高算法的局部开发能力。 表4 一阶时滞系统对比结果 收敛速度、收敛精度和避免局部最优能力是检验优化算法的重要指标[19-20]。图5为部分测试函数的收敛曲线。从单峰基准函数(F1、F3、F5、F7)上的曲线可以看出,CHBA的收敛精度明显高于其他算法,表明在加入自适应正态云模式后,在最佳蜜獾周围产生的多样化蜜獾种群提高了CHAB的开发能力。从多峰基准函数(F9、F11、F13)上的曲线可以看出,与其他算法相比,CHAB的收敛速度快,表明在更新最佳蜜獾位置时引入了加速度系数后,加速度系数为最佳蜜獾提供了向食物位搜索范围,避免了无效搜索,加快了搜索速度。此外,通过观察固定维多峰基准函数(F21、F23)的曲线可知,CHAB停滞的次数比其他算法少,即使CHAB陷入局部最优,也能随着迭代次数的增加快速跳出,收敛行为验证了CHAB的搜索与开发能力更为平衡,验证了CHAB的优越性。 (a) PID控制器的计算式为 (16) 其中,Ki=Kp/Ti;Kd=KpTd;e(t)表示偏差信号。 PID控制器中有3个参数,将维数取为3,总体设置为20,迭代次数为25。 在适应度函数的选择中,文献[19~22]使用时间乘积分绝对误差(Integral Time Absolute Error,ITAE)或以此为基础计算适应度值,如式(17)所示。 (17) 为了验证该算法的有效性,本文对一阶时滞、非最小相位系统和一阶最小延迟系统执行了PID控制器,并与基于蜜獾算法的PID参数自整定算法HBA-PID、基于粒子群优化的PSO-PID进行了比较,以测试该算法。3个受控对象的传递函数分别如式(18)~式(20)所示 (18) (19) (20) 式中,e为常数。 对于一阶时滞系统,通过不同参数自整定算法获得的PID参数自整定结果如表4所示。 从表4可以看出,在ITAE规则上,改进算法获得的结果优于其他PI自动调整算法。阶跃响应曲线如图6所示。 图6 一阶时滞系统阶跃响应Figure 6. Step response curve of the first-order plus time delay system 从图6可以看出,改进算法在时间调整方面具有更好的性能。虽然由于ITAE规则的影响其仍然存在超调,但如果根据超调量修改适应度函数,系统的超调量将相应减小。 对于非最小相位系统,不同参数获得的PID参数自动调谐结果如表5所示。 表5 非最小相位系统对比结果 从表5可以看出,虽然改进算法在ITAE规则上获得的结果优于粒子群算法和HBA,但与HBA相比,改进算法克服了容易陷入局部优化的缺点。阶跃响应的仿真结果如图7所示。 图7 非最小相位系统阶跃响应曲线Figure 7. Step response curves of the non-minimum phase systems 从图7可以看出,改进算法获得的结果在调节时间上优于其他系统,HBA与WOA则陷入了局部最优,无法跳出。 对于一阶最小延迟系统,不同参数获得的PID参数自动调谐结果如表6所示。 表6 一阶最小延迟系统对比结果 从表6可以看出,改进算法在ITAE规则上获得的结果优于粒子群算法和HBA。 一阶最小延迟系统阶跃响应的仿真结果如图8所示。 图8 一阶最小延迟系统阶跃曲线Figure 8. Step response curves of the first-order minimums lag systems 从图8可以看出,在上升时间、超调量和稳定时间方面,改进算法具有较大优势。改进算法的超调量在系统响应方面明显优于其他参数自整定算法优化的系统。 通过对3个典型系统的优化仿真可以看出,在ITEA规则下,基于正态云的引力加速HBA的PID参数整定算法相较其他PID参数整定算法具有一定优势。 本文提出了一种基于引力加速搜索和正态云的蜜獾算法。通过引入加速系数控制蜜獾算法中密度因子控制搜索范围,并利用正态云提高蜜獾种群的多样性。从标准差和平均值等统计结果以及收敛曲线来看,本文所提CHBA算法具有更好的收敛速度和精度以及跳出局部最优解的能力,在全局搜索和局部开发能力上性能较为平衡。后续研究将进一步通过工程实际优化问题验证该算法的有效性。2 仿真结果与分析
2.1 单峰基准函数测试
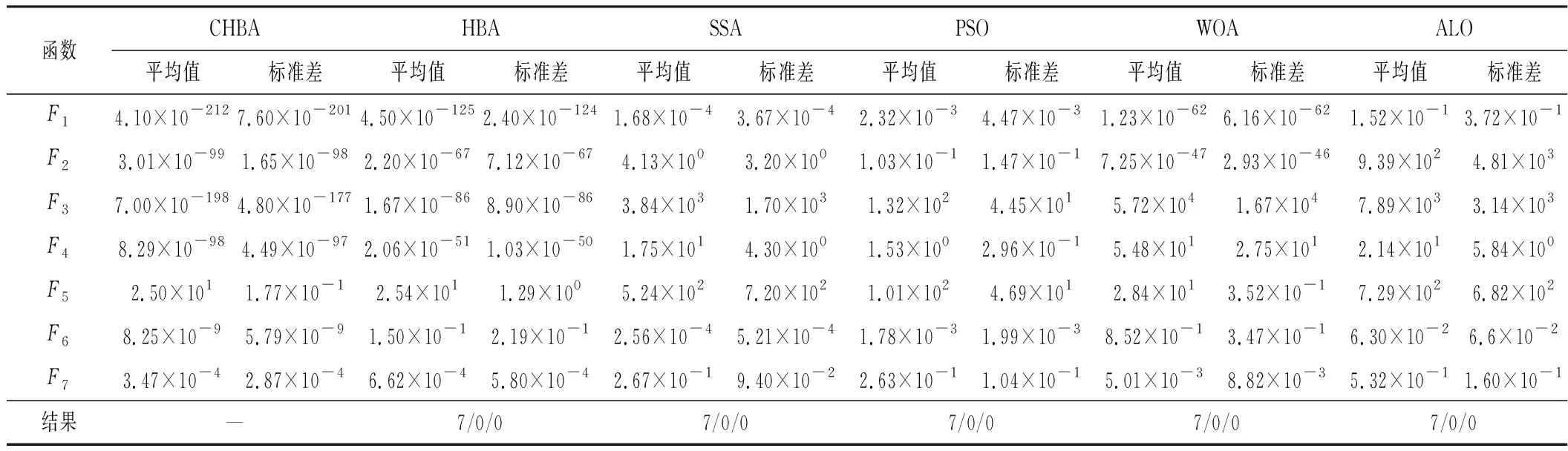
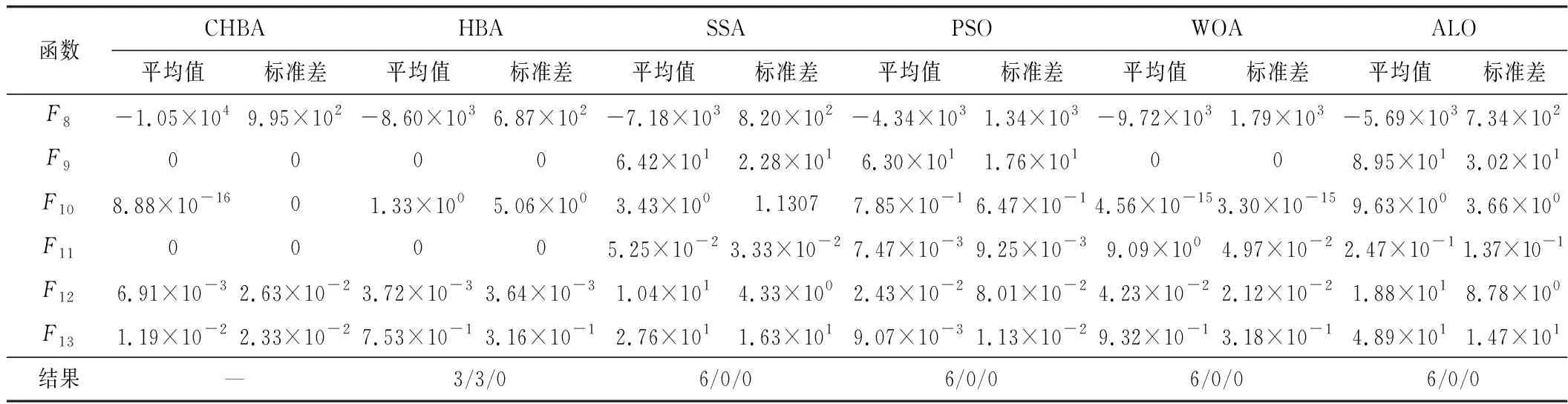
2.2 多峰基准函数测试
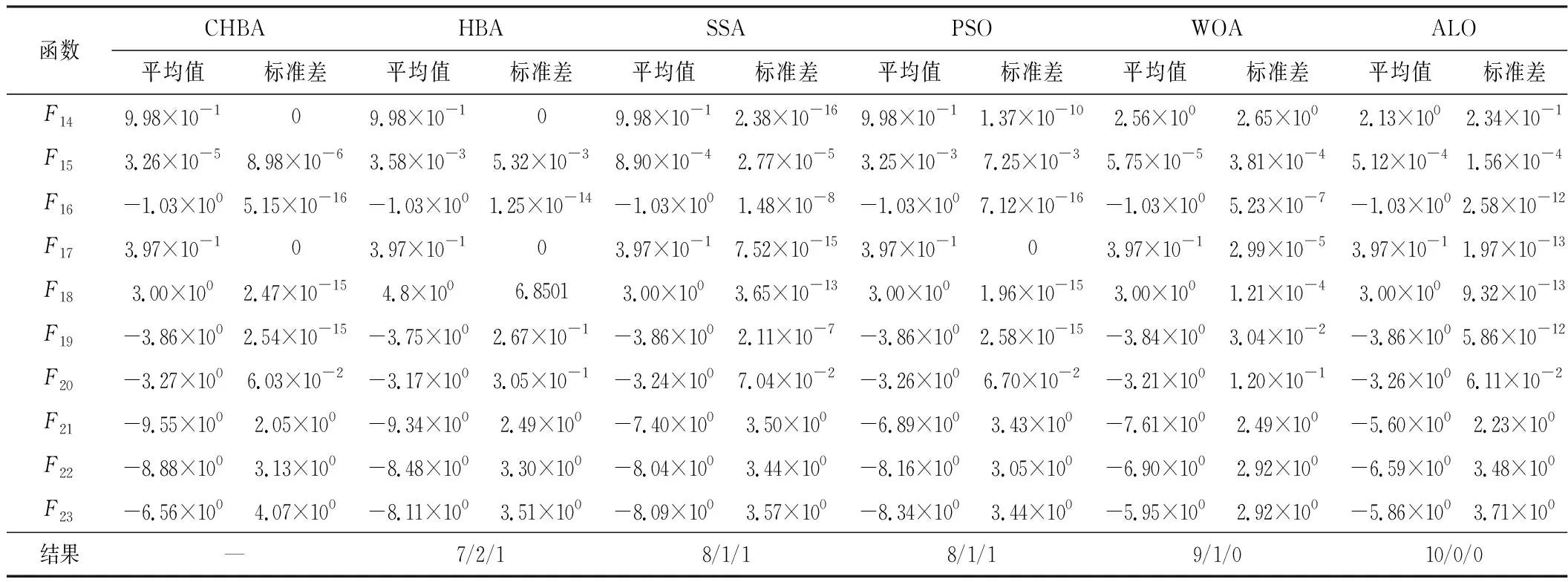
2.3 固定维多峰基准函数测试
2.4 收敛曲线对比
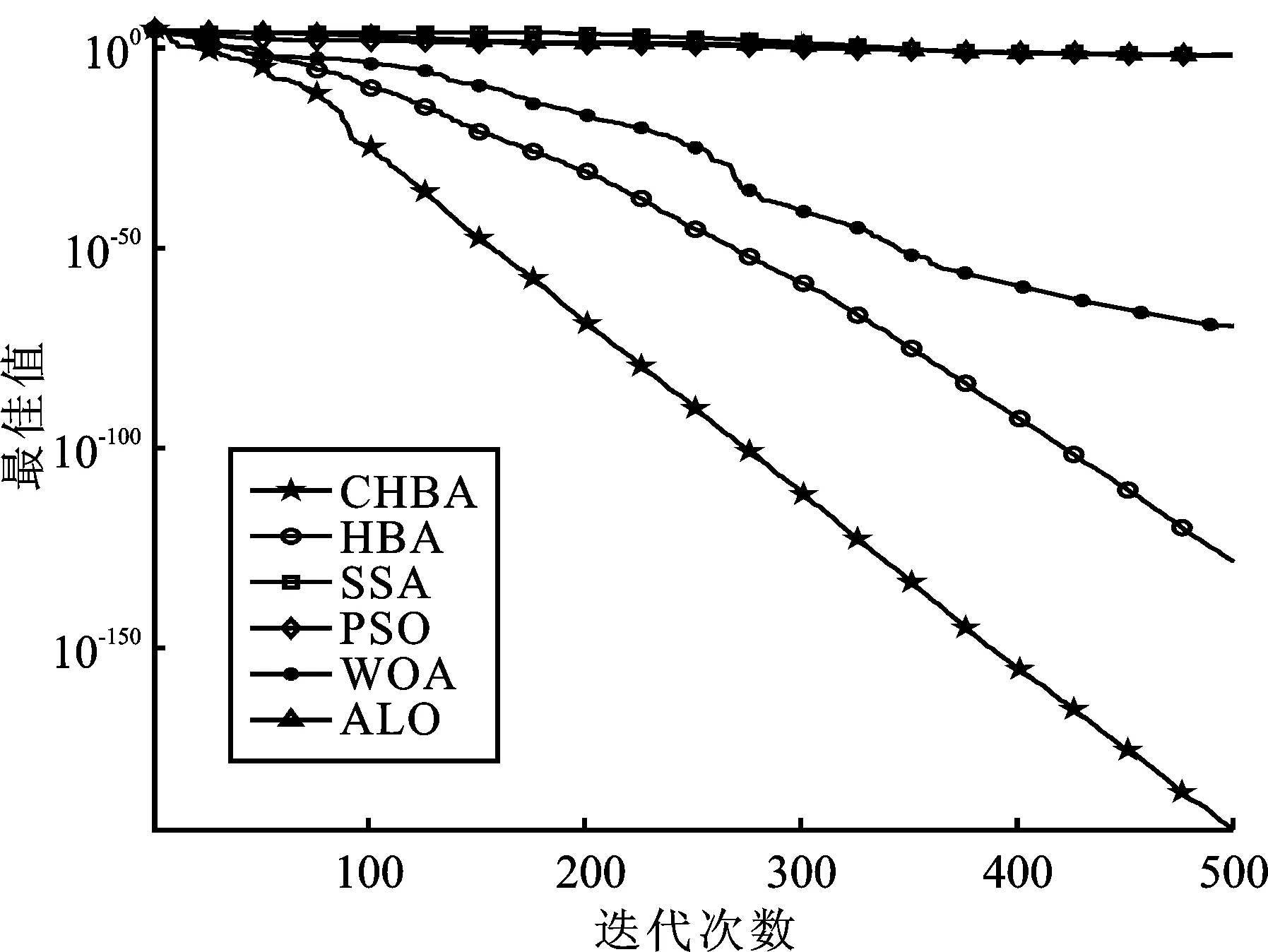
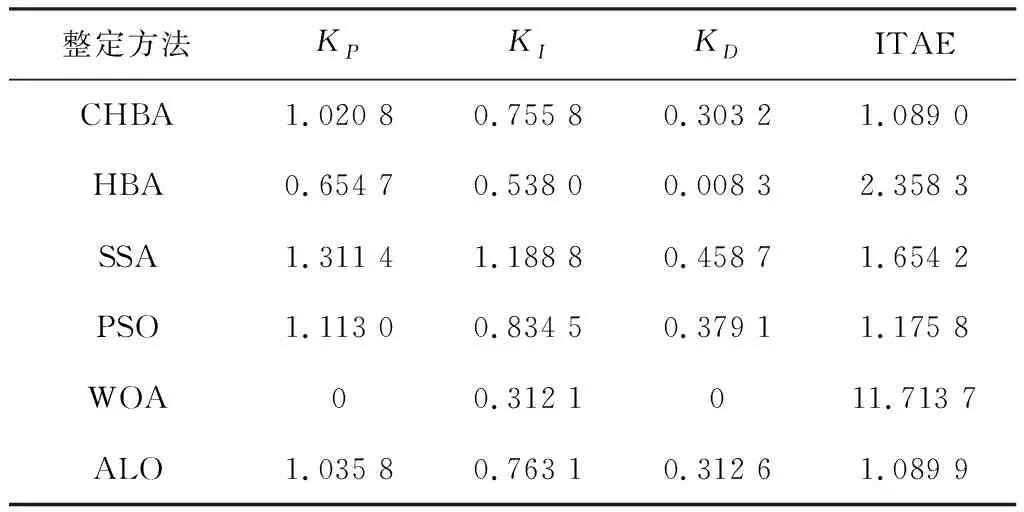
2.5 PID参数自动整定
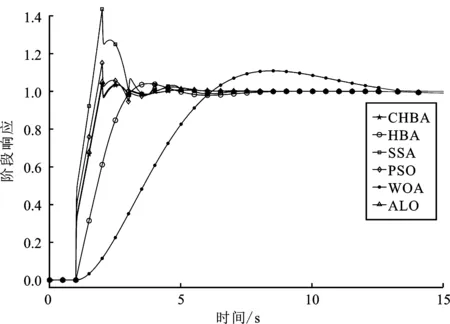
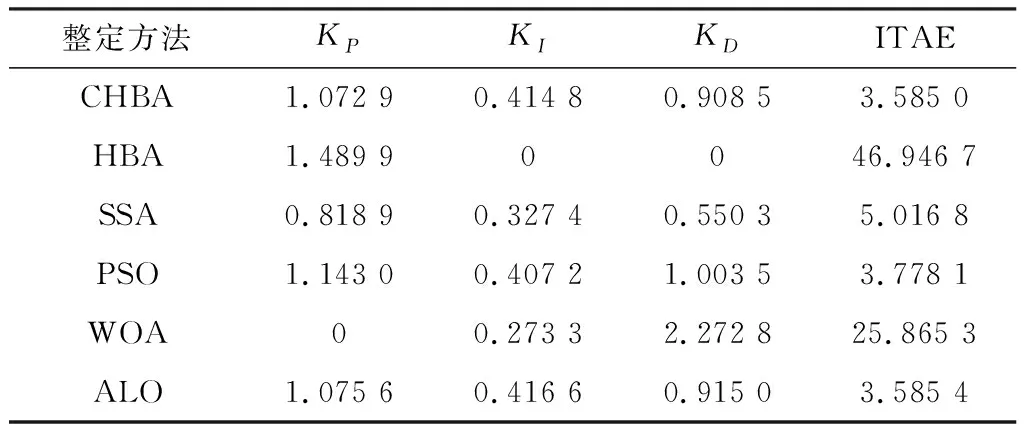
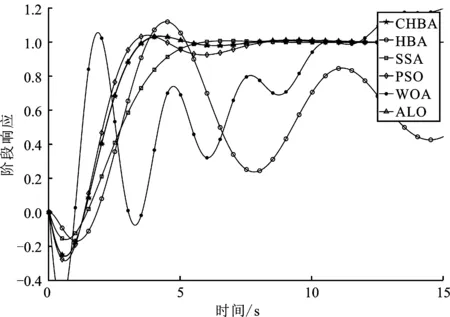
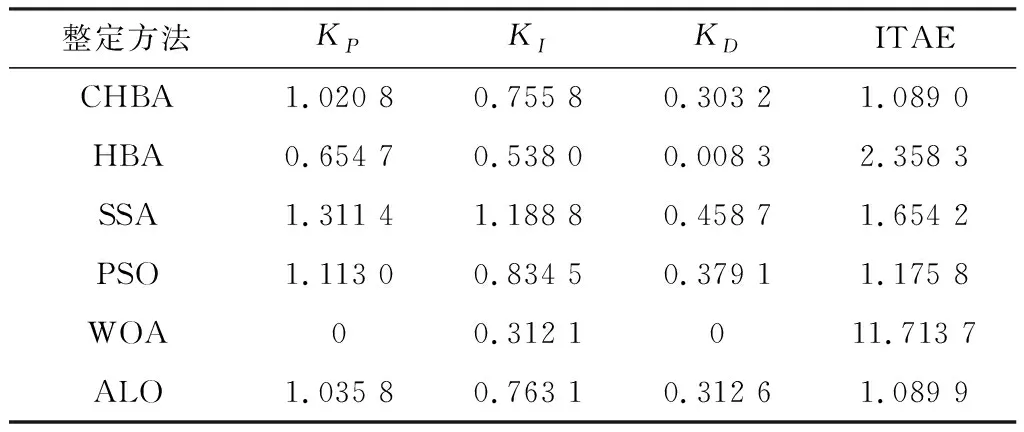
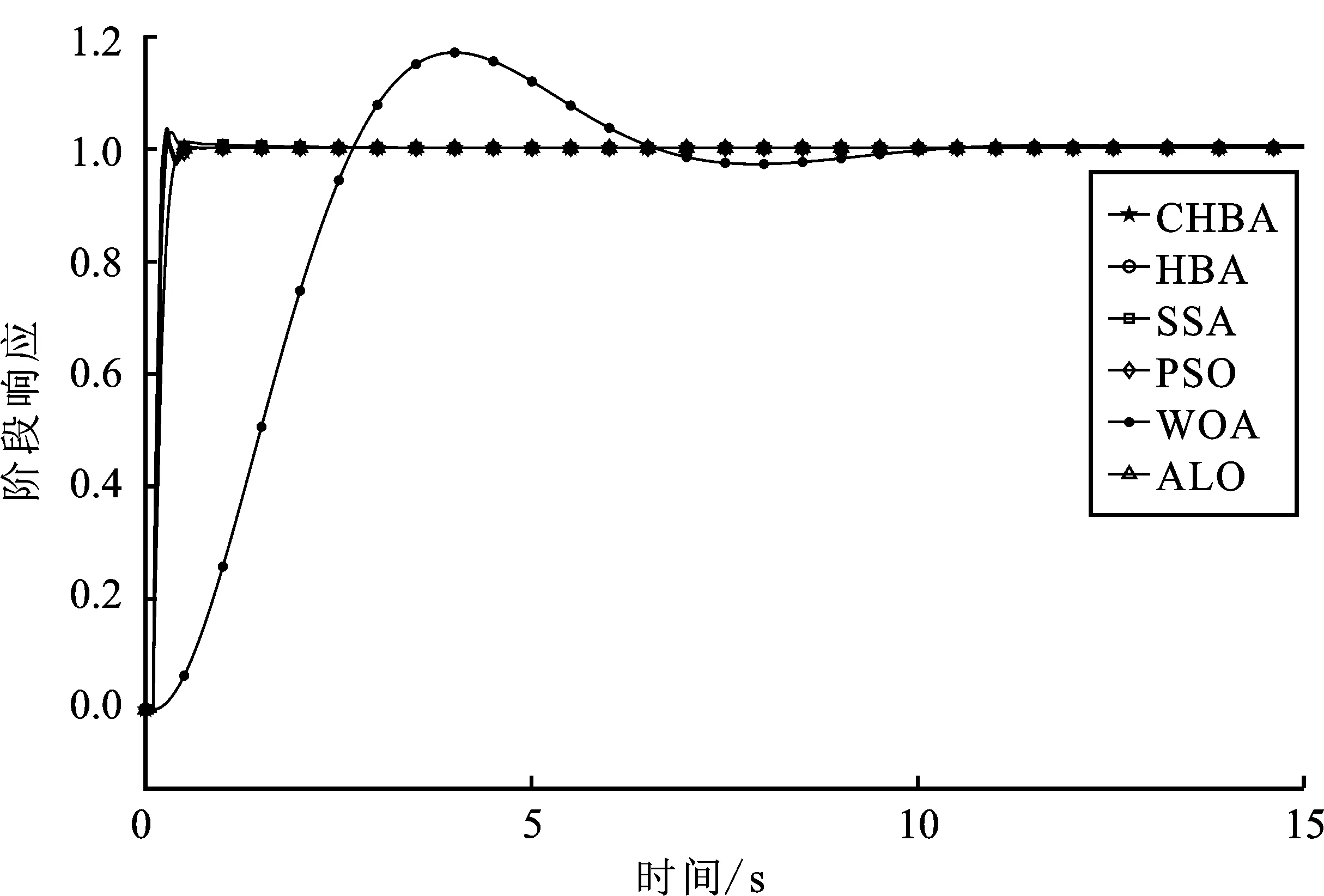
3 结束语
