IMMKF与Chan-Taylor算法的协同定位

王欣悦,余慧敏,胡露宁

(湖南师范大学 信息科学与工程学院,湖南 长沙 410000)

超宽带(Ultra Wide-Band,UWB)定位技术是一种区别于传统通信方式的新通信技术,其主要采用的测距方法包括接收信号强度(Received Signal Strength Indication,RSSI)、信号到达时间(Time of Arrival,TOA)、信号到达时间差(TDOA)以及信号到达角度(Angle of Arrival,AOA)[1]。TOA和TDOA的定位精度较AOA高,故室内定位主要采用TOA和TDOA作为测距方法,根据飞行信号的相关时间信息解算目标的位置信息。基于TDOA的测距多采用多节点TDOA法,再根据测量的TDOA值建立双曲线方程求解交点,由数学原理可知该点为目标节点位置坐标[2]。求解双曲线的主要算法有最小二乘法、三边定位算法、Chan算法、Taylor算法以及Fang算法[3],每种算法对TDOA测量值的误差特性要求均不同,计算的复杂性也各不同,不同算法在不同TDOA噪声特性下能达到定位估计的最优解或次优解。上述几种求解算法面临一个共同问题,即在信道环境较差情况下,定位精度较低,较难满足定位精度的要求,故多数研究选择使用融合算法对坐标进行解算。

TDOA测距定位方法在理论上能够达到相对理想的定位精度,但仍会因为硬件设备与环境因素引起噪声,其主要包括非视距误差和多径效应引起的信号误差[4]。由于卡尔曼滤波算法具有良好的滤波效果,研究人员选择使用卡尔曼滤波来消除误差,提高定位精度及性能。早期基于卡尔曼滤波的研究主要集中在直接处理测量值。文献[5]提出先使用卡尔曼滤波处理TOA测量值,消除误差,再进行TOA定位,理论和实验均表明该方法的定位结果优于单纯的TDOA测距方法。文献[6]提出了基于扩展卡尔曼滤波器的混合TDOA/TOA室内定位方法,判断TDOA和TOA测量值有无NLOS(Non-Line-of-Sight)误差,有则使用卡尔曼滤波,并将处理后的结果与优选AOA值一起代入扩展卡尔曼滤波器中,最终算出目标位置坐标。文献[7]首次提出卡尔曼滤波算法和Chan算法相结合的算法,将各种卡尔曼滤波算法与Chan算法结合再进行目标位置解算,实验结果表明结合卡尔曼滤波算法后定位精度更高。文献[8]提出了Chan-Kalman定位算法,用Chan算法的位置估计值作为Kalman滤波的初始值,有效提高了室内定位的精度和稳定性。文献[9]将IMM算法与卡尔曼滤波算法结合,利用TWS雷达数据跟踪机动目标,显著提升了跟踪目标的定位精度。基于以上研究,本文提出一种结合交互式多模型IMM算法的Chan-Taylor-IMMKF室内定位算法,将Chan-Taylor算法解算的坐标估计值代入卡尔曼滤波器的观测矩阵来作为卡尔曼滤波器的观测值。同时,使用IMM算法建立3个模型,根据滤波器的估计值匹配合适的模型进行正规滤波,再将各个模型的定位结果进行加权融合,以此达到提高定位精度的效果。

1 UWB室内定位技术

超宽带(UWB)是一种无线通讯技术,使用持续时间较短、占空比较低的窄脉冲信号,故在目前所知的室内定位技术中其定位精度最高。超宽带无线通信原理如图1所示[10],在发送端脉冲发生器产生信号脉冲,通过调制器实现信息传输;在接收端,被接收到的信号经过低噪声放大器放大,然后通过匹配滤波器和相关接收机处理,被门限电路恢复信号携带的信息。

UWB定位主要分为测距与解算两个过程。本文采用TDOA定位算法测距,其根据标签到各个定位基站的到达时间差解算标签位置[11],测距主要实现方式是多节点TDOA法,其原理如图2所示。

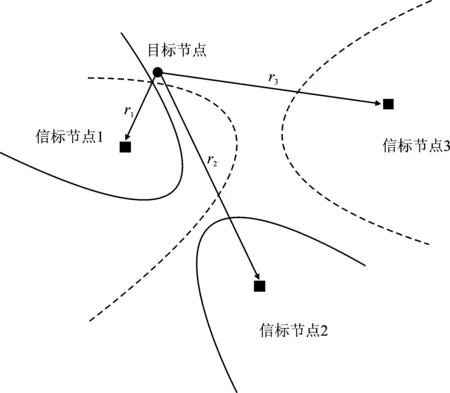
图2 多节点TDOA法Figure 2. Ulti-node TDOA method

多节点TDOA法的基本原理是双曲线的数学性质,即双曲线的点到两焦点的距离之差为一个定值。如图2所示,包括以信标节点1、信标节点2为焦点的一组双曲线方程及以信标节点2、信标节点3为焦点的一组双曲线方程,联立两组双曲线方程,解算方程得出交点即为目标节点坐标。数学描述为:目标节点所发射的信号到达3个信标节点的时延分别为t1、t2和t3,则可算出目标节点和每个信标节点的距离分别为

r1=c×t1
r2=c×t2
r3=c×t3

(1)

其中,c是电磁波在空气中的传输速度,为3×108m·s-1。进一步便可求得目标节点与信标节点之间的距离差,为

(2)

信标节点的坐标已知,直接将第i个节点的坐标表示为(xi,yi),将目标节点的坐标设为(x,y),由数学原理可建立双曲线方程

(3)

将式(2)代入式(3)可解出这对双曲线的交点,即为目标节点坐标。上述双曲线求解算法主要为Chan算法和Taylor算法[12]。求解目标节点位置坐标之后,为提高精确度再使用滤波算法滤除噪声。

2 Chan-Taylor-IMMKF室内定位算法

2.1 Chan-Taylor加权算法

Chan算法是非递归双曲线方程组的一种解法[13],当噪声服从高斯分布时其具有定位精度大、误差小的特点,而且通过信标节点的数量可以提高定位精度。Taylor算法是一种迭代算法[14],首先在泰勒级数展开的基础上使用初始迭代值进行加权最小二乘法估计,再解出位置估计误差的局部最小二乘解,更新目标节点的位置估计。

Chan算法和Taylor算法对误差处理方式不同,计算复杂程度也不同,故将两种算法的优点结合提出Chan-Taylor加权算法。Chan-Taylor加权算法避免了Taylor算法由于初始值与真实值相差较大时分散的问题,也减小了NLOS误差定位精度的影响。算法具体实现方法为:先使用Chan算法解算TDOA测量值,将该位置估计值作为Taylor级数展开算法的初始值进行迭代,对位置进行再次估计。为了减少级数发散问题,将Chan算法解算的位置估计值和Taylor算法的位置估计值均进行加权计算,最终得出位置估计值。具体加权过程[15]为:

1)计算解算结果与测量值之间的残差

(4)

式中,N为信标节点数量;X为位置估计值;Xi为第i个信标节点坐标;

2)为了提高定位精度,将残差归一化

(5)

式中,第k种算法的加权系数为Rk。

3)加权计算得最终位置估计结果,如式(6)所示。

(6)

2.2 传统卡尔曼滤波算法

卡尔曼滤波算法是一种最优化自回归数据处理算法,能够估计平稳的一维随机过程,也能够估计非平稳的、多维随机过程,且卡尔曼滤波算法递推,易于在计算机上实现[16]。卡尔曼滤波算法通过正态分布进行递推处理,对最优值的估计分为两个阶段[17]:1)利用上一时刻的位置状态对当前时刻的位置进行预测估计;2)使用当前时刻带有噪声的观测值对估计值进行修正。其具体实现方程如下:

预测过程为

(7)

(8)

(9)

(10)

更新过程分为3步,分别如式(11)～式(13)所示

(11)

(12)

Pk|k=(I-KkHk)Pk|k-1

(13)

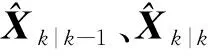
2.3 Chan-Taylor-IMMKF定位算法

Chan-Taylor加权算法已达到相对准确的定位精度,但仍存在环境误差,采用卡尔曼滤波可以从概率统计角度估计并消除误差,提高系统的定位性能。卡尔曼滤波器是线性滤波器,基本原理是根据上一时刻系统状态的预测状态推测下一时刻系统的真实状态,故卡尔曼滤波器需要满足线性条件。但当定位对象忽然改变运动状态时,卡尔曼滤波可能会“滞后”影响定位结果。本文提出Chan-Taylor-IMMKF定位算法,使用自适应算法——交互式多模型算法IMM来提高定位精度。IMM算法主使用多个卡尔曼滤波器并行处理数据,每个滤波器对应不同的状态空间模型,最后通过有效加权融合进行系统状态估计,克服了单模型估计误差较大的问题,提高了定位性能。Chan-Taylor-IMMKF的完整算法流程如图5所示。

在图3中,算法主要由两部分组成,第一部分是Chan-Taylor加权算法解算目标节点位置估计,第二部分是IMMKF算法滤波。Chan-Taylor加权算法先通过Chan算法解算TDOA测量值,再将结果作为Taylor算法的初始迭代值继续计算,最后将两种算法的结果进行残差加权得出位置估计值。IMMKF算法使用多个对应不同状态空间模型的卡尔曼滤波器并行处理,并将Chan-Taylor加权算法得到的目标节点位置估计值作为IMMKF算法的估计状态[18]。IMM算法的主要思想是假设一个模型相对于其他模型在此刻有效,通过混合前一时刻所有滤波器状态估计值,获得与此特定模型相互匹配的滤波器初始条件,然后再对模型库中的每个模型进行常规滤波,并加权融合每个滤波器的输出结果,得到最终状态估计。具体实现步骤为:

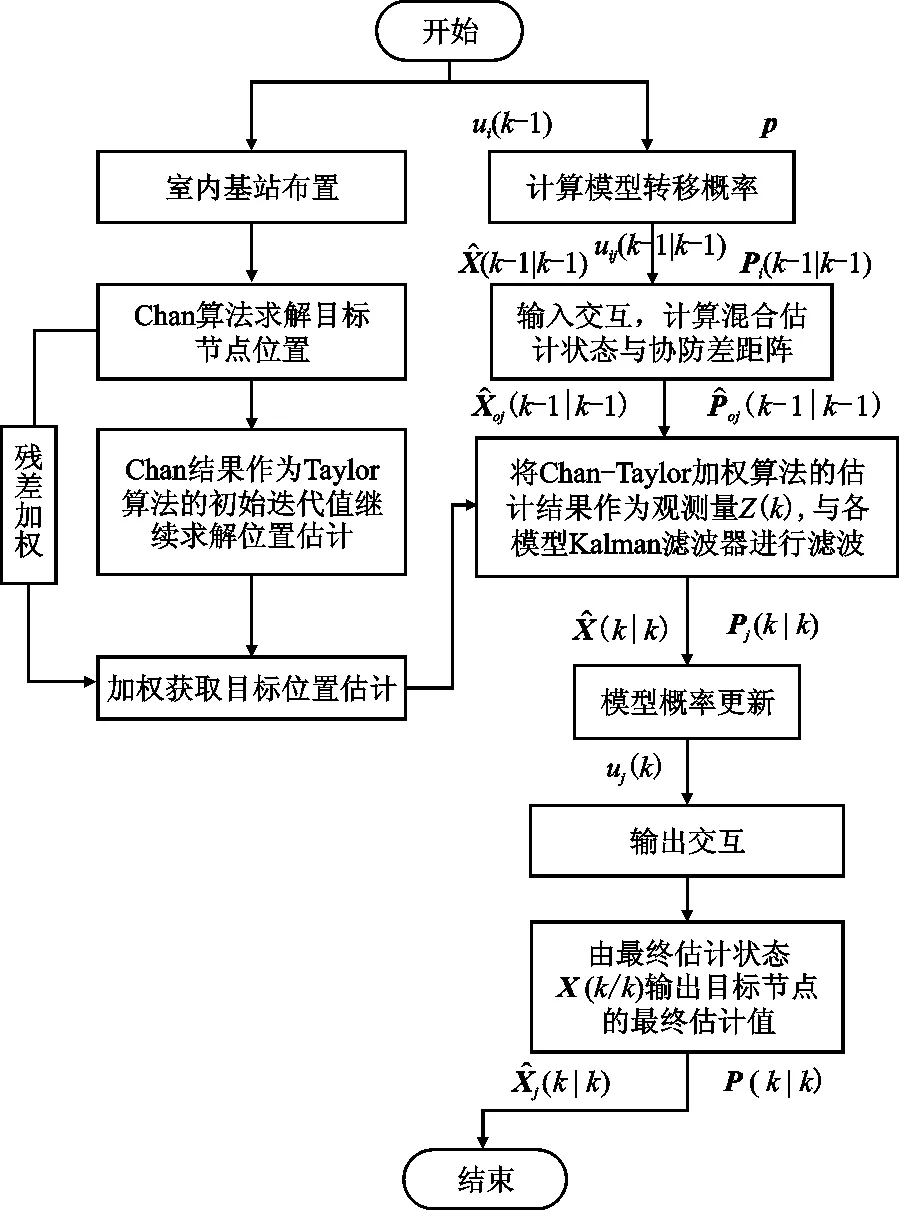
图3 Chan-Taylor-IMMKF算法流程Figure 3. Flow of Chan-Taylor-IMMkF algorithm

步骤1计算模型混合概率。假设目标有r种运动状态,对应r个运动模型,第j个模型表示的目标状态方程为

Xj(k+1)=Φj(k)Xj+Gj(k)Wj(k)

(14)

观测方程为

Z(k)=H(k)X(k)+V(k)

(15)

式中,Wj(k)是过程噪声,是均值为零、协方差矩阵为Qj的独立多元正态分布。元素pij是目标由第i个运动模型转移到第j个运动模型的概率,通过马尔可夫状态转移矩阵确定转移矩阵,具体为

(16)

模型i的预测概率(归一化常数)为

(17)

模型i到模型j的混合概率如式(18)所示。

(18)

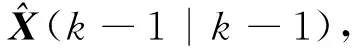
(19)

混合协方差矩阵为

(20)

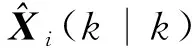
步骤4模型概率更新。采用似然函数更新uj(k)

(21)

Λj(k)似然函数为

(22)

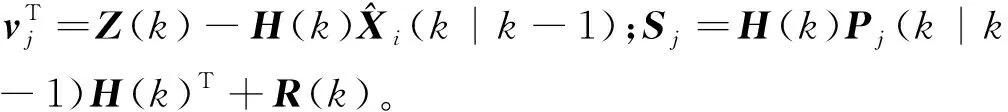
步骤5输出交互。基于模型概率,将每个滤波器滤波的估计状态进行加权合并,得到总估计状态和协方差矩阵,输出最终结果即为目标节点的估计坐标。

计算总估计状态为

(23)

协方差矩阵为

(24)

对所有滤波器的结果进行加权平均,最终计算的值即为滤波器的输出,其中权重为模型概率。

3 计算结果分析

使用MATLAB软件对本文相关算法进行仿真,全面分析算法性能。

3.1 Chan-Taylor加权算法仿真

对Chan-Taylor加权算法进行仿真处理,查看定位效果。仿真场地为500 m×500 m,信标节点的布置遵从蜂窝网络原则,具体设为(0,0)、(500,0)、(500,500)、(0,500),如图4所示,目标节点的位置坐标是(50,100)。不考虑NLOS误差,仅考虑TDOA测量值误差,设定测量值误差为均值为0且标准差分别0.2、0.4、0.6、0.8、1.0的高斯噪声。

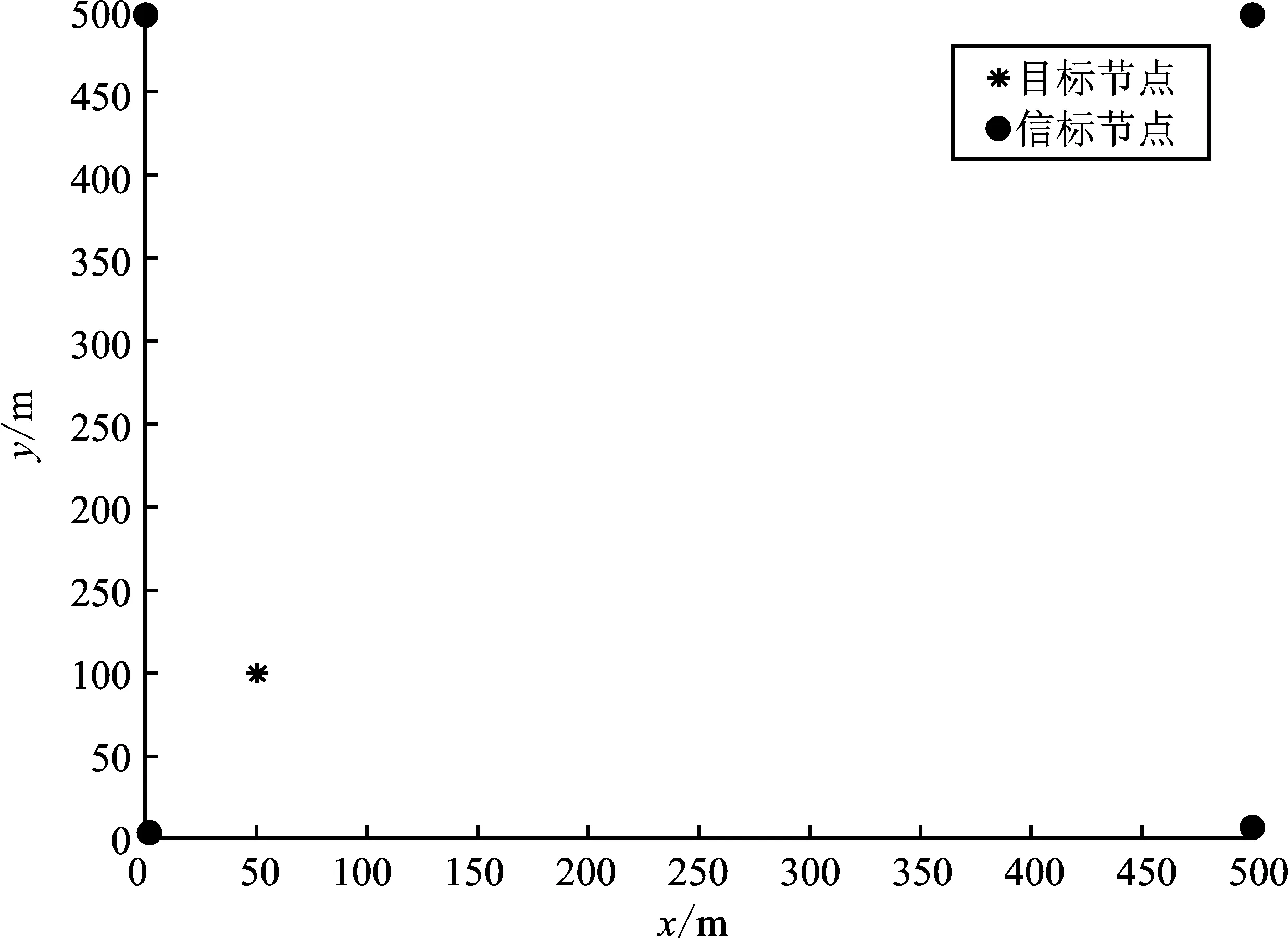
图4 目标与信标节点分布Figure 4. Distribution of target and beacon nodes

图5给出不同算法的平均定位误差标准差与噪声误差之间的关系。Chan-Taylor加权算法的定位误差比单纯Chan算法小,并且接近以真实值为初始迭代值的Taylor算法。虽然随着差的增大其定位误差依然增加,但整体定位效果有所提升。

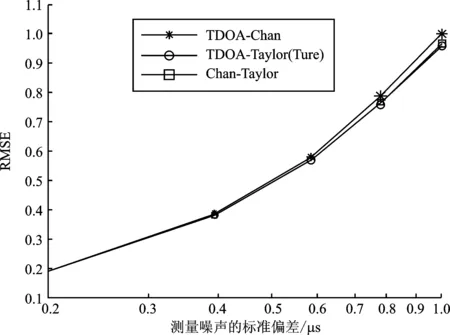
图5 3种算法误差标准差Figure 5. Error standard deviation of three algorithms

3.2 Chan-Taylor-IMMKF定位算法仿真

3.2.1 单种运动状态仿真

使用卡尔曼滤波算法进一步提升定位效果,主要仿真查看动态性能。仿真场地为5 000 cm×5 000 cm,信标节点具体设为(0,0)、(5 000,0)、(5 000,5 000)、(0,5 000),目标为动态,目标节点的初始节点坐标为(50,100)。运动状态为匀速运动,设x方向的速度均为2 cm·s-1,y方向的速度为20 cm·s-1,在目标运动过程中加入均值0的高斯过程噪声。TDOA测量值误差设定仍为均值为0,标准差分别0.2、0.4、0.6、0.8、1.0的高斯噪声,每次仿真次数为120次。使用卡尔曼滤波算法处理Chan-Taylor加权算法的估计值,观察结果。

图6为是否使用卡尔曼滤波算法的位置估计曲线图,可看出融合卡尔曼滤波算法之后的轨迹更接近真实轨迹,而Chan-Taylor加权算法的轨迹波动较大,表明Kalman滤波器可以有效减小误差来提高精度。图7为两种算法的定位误差对比,可看出Chan-Taylor加权算法最大误差值达到了42 cm,而卡尔曼滤波算法的误差值在15 cm以内,定位效果有所改善。

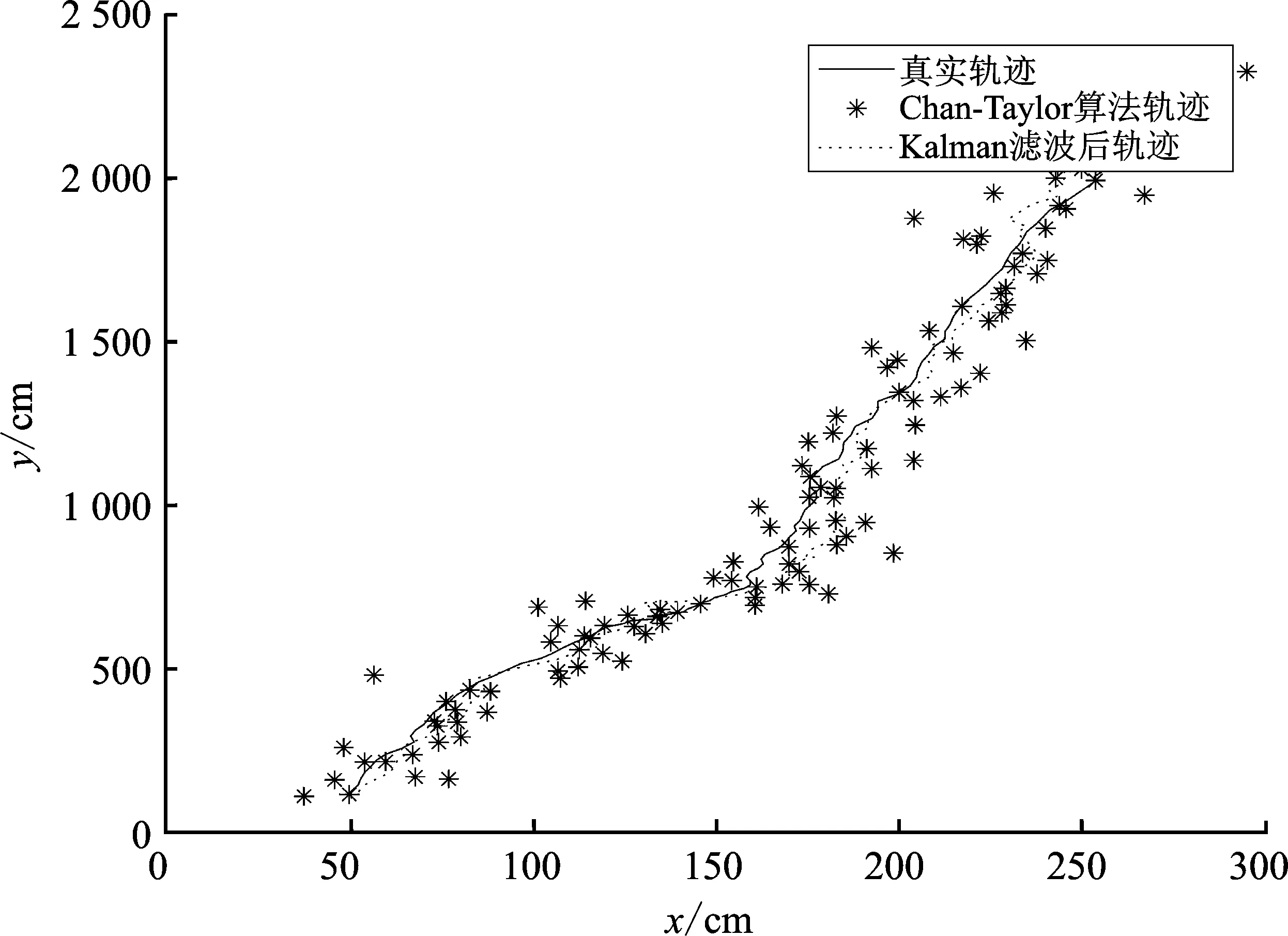
图6 目标节点轨迹对比Figure 6. Trajectory comparison of target nodes

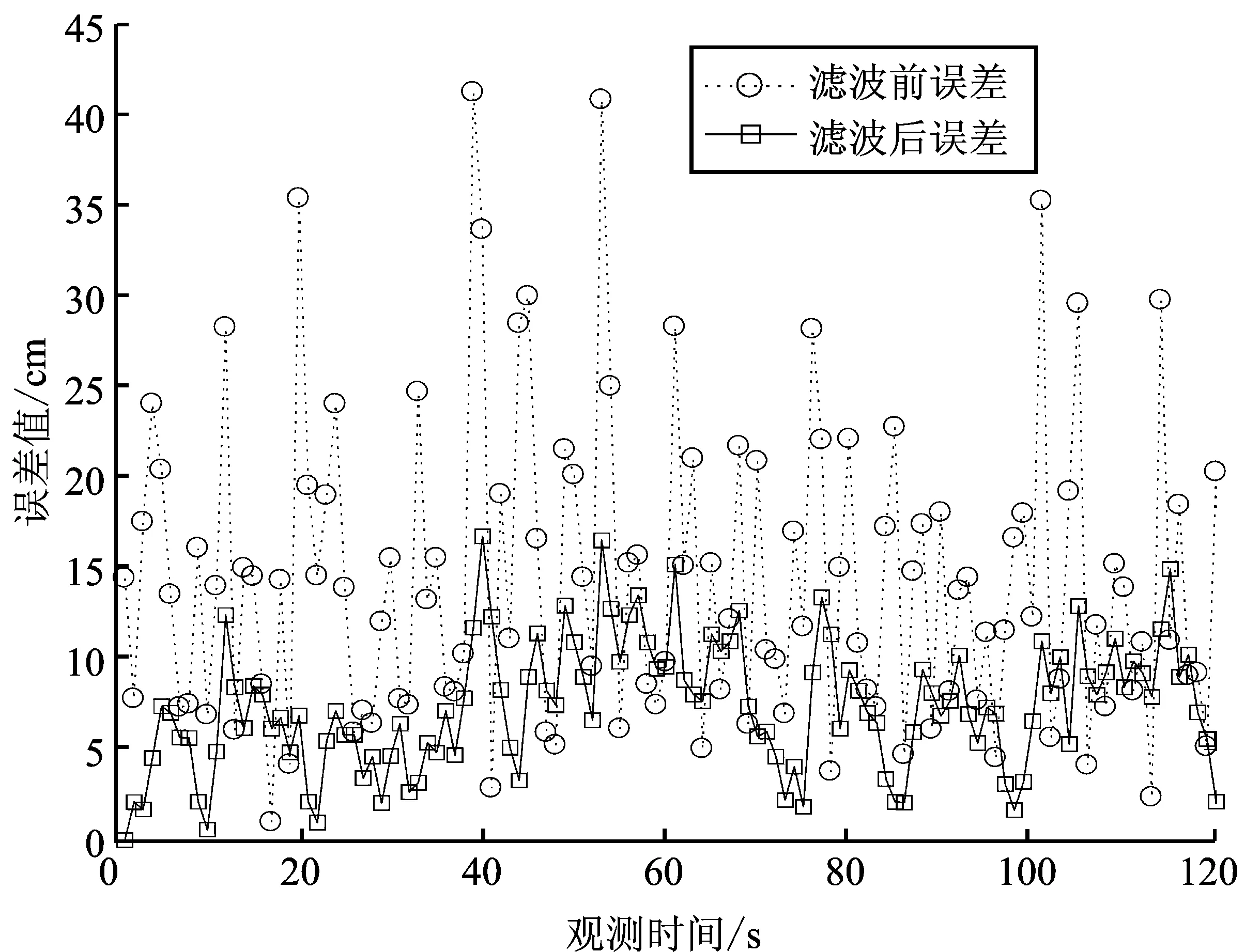
图7 目标节点定位误差对比Figure 7. Comparison of location errors of target nodes

3.2.2 多种运动状态仿真

图8为目标节点运动轨迹对比,可看出在0～400 s内,卡尔曼滤波的滤波轨迹接近真实轨迹。在400 s处目标节点快转弯改变运动状态,卡尔曼滤波轨迹偏离真实轨迹。目标节点回归一种运动状态后,卡尔曼滤波轨迹逐渐回归真实轨迹。与卡尔曼滤波轨迹相比,Chan-Taylor-IMMKF算法的滤波轨迹在0～600 s时间内全程靠近真实轨迹,在600 s处出现短暂偏离也可及时修正,表明Chan-Taylor-IMMKF算法可以较好地处理误差。由两种算法的滤波轨迹对比可看出,Chan-Taylor-IMMKF算法能够较好地避免因为目标忽然改变运动状态卡尔曼滤波算法滞后不能及时跟踪的问题,其滤波轨迹更接近真实轨迹。

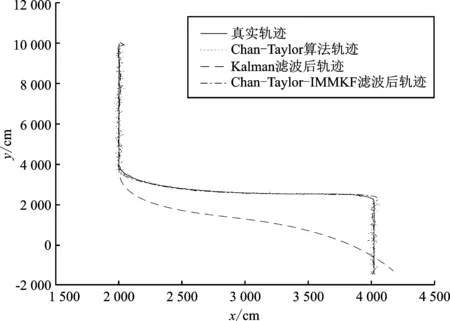
图8 目标节点轨迹对比Figure 8. Trajectory comparison of target nodes

图9为传统卡尔曼算法与Chan-Taylor-IMMKF算法对x、y方向独立观测的误差对比。由误差曲线可看出在0～400 s内,卡尔曼滤波与IMMKF滤波的效果均可达到定位需求,在400 s处卡尔曼滤波算法定位误差开始大幅增加,到运动停止未恢复; Chan-Taylor-IMMKF算法在600 s处x、y方向均出现较大误差,但其在较短时间内恢复滤波效果,整体满足定位需求。

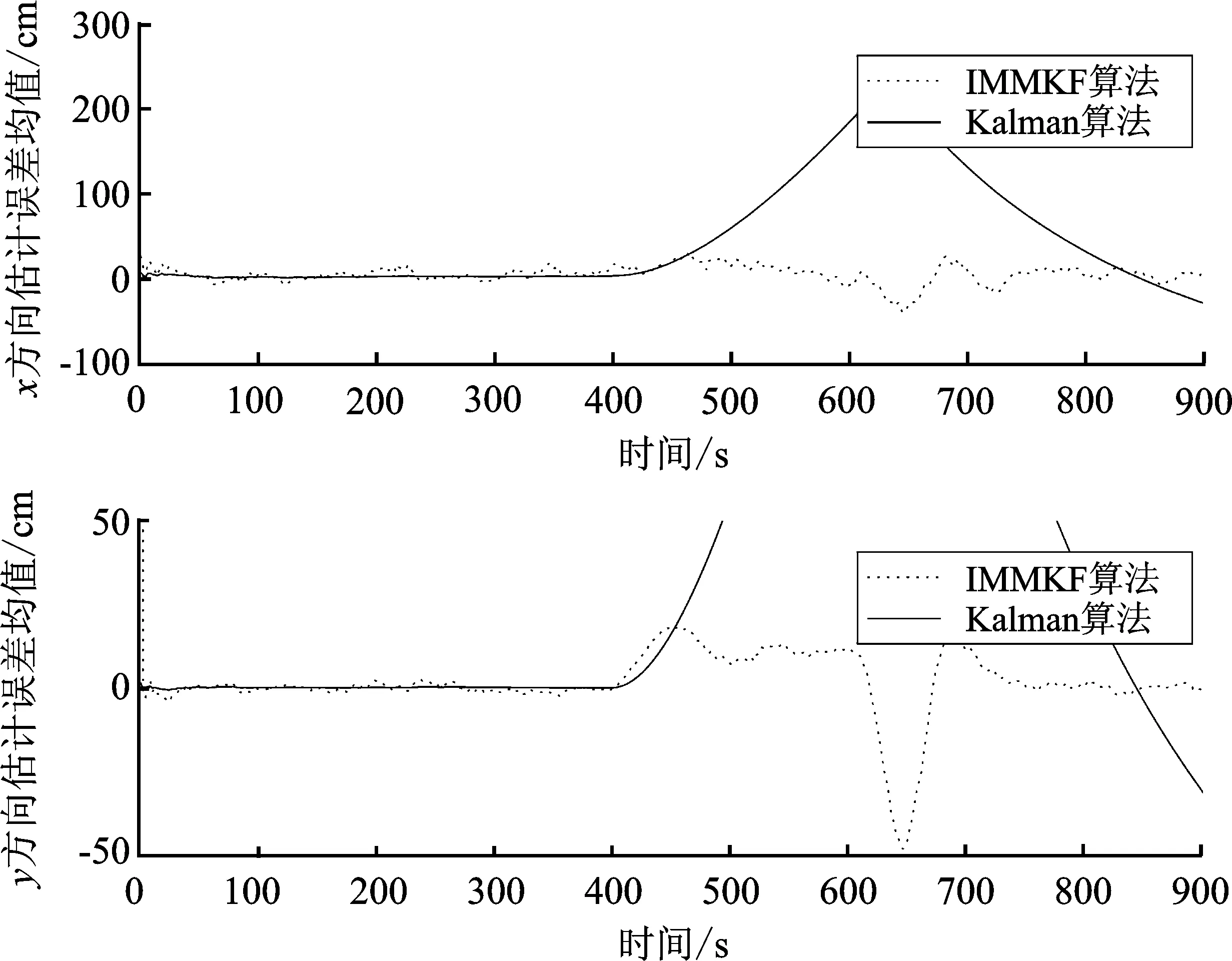
图9 滤波误差的均值曲线 Figure 9. Mean curve of filtering error

图10为Chan-Taylor算法未滤波与Chan-Taylor-IMMKF算法滤波的误差标准差对比,可以看出在600 s处误差较大,但可及时修正并快速恢复滤波效果,整体上滤波处理后的误差小于不滤波处理的误差。表1为误差结果具体数值对比,使用融合交互式多模型的卡尔曼滤波算法后的误差均值为之前的一半,误差均值控制在15 cm以内,说明滤波效果显著。虽然本文所提方法的效果小于匀速运动时卡尔曼滤波算法,但多种运动状态时该误差符合定位需求,相比于单独卡尔曼滤波算法,IMMKF滤波轨迹更接近于真实轨迹。

表1 定位误差对比

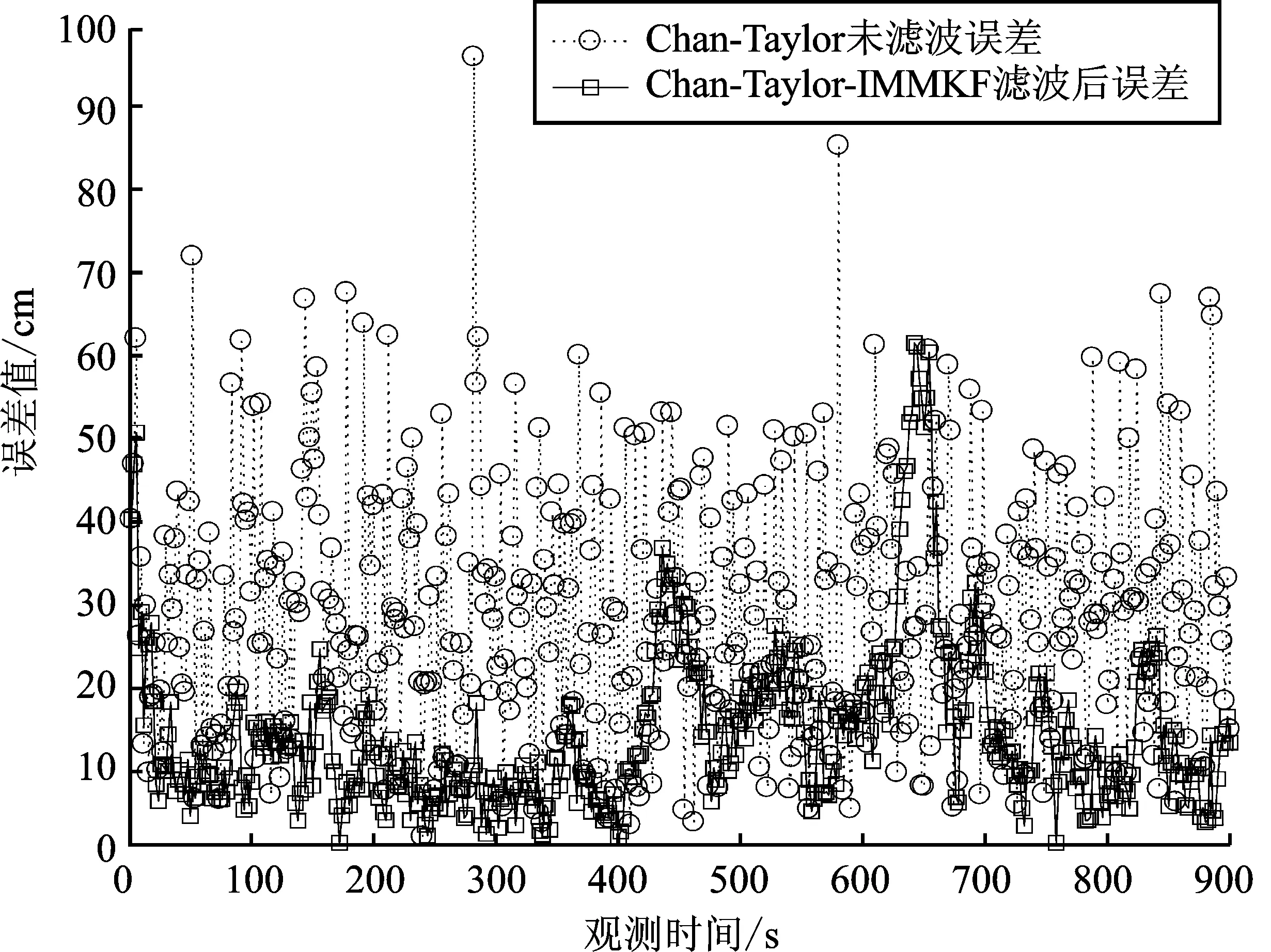
图10 目标节点滤波误差对比 Figure 10. Comparison of filtering errors of target nodes

4 结束语

本文分析了基于TDOA定位模型解算目标节点位置估计的Chan算法和Taylor算法,针对Chan算法由于NLOS精度降低与Taylor算法发散问题提出了加权Chan-Taylor算法,将Chan算法的估计值作为Taylor算法的初始迭代值,将两个算法的估计值进行残差加权得到融合估计值,提高了定位精度,降低了NLOS误差,使误差标准差接近于以真实值迭代的Taylor算法。针对传统卡尔曼滤波器由于目标节点忽然改变运动状态产生“滞后”问题,提出了Chan-Taylor-IMMKF算法,将残差加权Chan-Taylor算法的估计值作为IMMKF的测量值。实验结果表明,该算法可以较好地避免目标改变运动状态不能及时跟踪的问题,将误差均值控制在15 cm左右,提高了定位性能。该方法具有普适性,可广泛用于室内定位与机动目标跟踪。在后续研究中,可对其继续进行优化,提高精度,并将其应用于多目标跟踪定位。