多变量乘用车销量预测模型研究

2023-12-05段昊江吴冰

汽车文摘 2023年12期

关键词：乘用车销量变量

段昊江吴冰

（同济大学经济与管理学院，上海 201800）

缩略语

ARMA Auto-Regressive Moving Average Model

RBF Radial Basis Function

SARIMA Seasonal Auto-Regressive Moving Average Model

BP Back Propagation

GDP Gross Domestic Product

VECM Vector Error Correction Model

XGBOOST eXtreme Gradient Boosting

VAR Vector Autoregressive Model

CNN Convolutional Neural Network

MSFM Multivariate Sales Forecasting Model

CPI Consumer Price Index

GDBT Gradient Boosting Decision Tree

MAPE Mean Absolute Percentage Error

SVR Support Vector Regression

0 引言

近年来，随着国民经济的高速发展和居民可支配收入的不断提高，我国乘用车市场已经趋于饱和，乘用车市场消费主力萎缩，加之近几年我国城市公共交通系统的完善、高铁线路网的扩散、城市限行等因素的作用，导致了汽车销量的低迷。2020 年，我国乘用车销量为2 006万辆，创近年新低。2021年，随着国内疫情逐步得到控制，乘用车行业逐渐回暖，全国乘用车销量达到2 175 万辆。2022 年，乘用车销量更是上涨到2 309 万辆。在汽车行业日渐繁荣的大环境下，无论是已经在市场中占据席位的车企还是打算进入汽车行业的“新人”，都应认真剖析市场现状格局和国家政策，准确把握行业发展方向，精准识别消费者需求，从而制定相适应的生产目标，实现按需生产。

在乘用车销量预测研究中，对于变量的选择，早期大部分学者只基于历史销量数据展开预测[1-2]，虽然预测模型与结果对市场长期性的变化有着比较好的效果体现，但是当市场出现波动时，时间序列模型的预测精度就会大幅度降低。有研究发现宏观经济因素会对乘用车的销量产生很大影响，是非常重要的外部因素，国内外学者开始考虑将宏观经济指标作为变量添加到模型中进行预测研究[3-5]。近年来，随着互联网和大数据的发展，消费者们几乎都喜欢在网络中搜索自己想购买的商品，并将网络中的相关信息和其他消费者的评价作为自己是否消费的参考。网络搜索数据为商品市场发展动向和趋势提供了一定程度的前瞻，越来越多的学者都开始应用时效性更好的网络搜索数据来进行乘用车的销量预测研究[6-10]。

但是，国内外学者们在进行乘用车销量预测的研究时，大多只选取一到两类影响变量进行研究，少有将上述变量类型综合起来同时进行考虑的研究，因此，本文在已有研究的基础上，以乘用车整体市场为研究对象，逐步添加历史销量、宏观经济指标、网络搜索关键词这些影响乘用车销量的变量，建立销量预测模型并进行效果比对分析。

1 文献综述

在乘用车销量预测方面，现有研究中考虑到的变量主要包括历史销量、宏观经济指标、网络搜索数据等，按照变量的选择与组合可以分为基于单类型变量的销量预测研究和基于双类型变量的销量预测研究。

1.1 基于单类型变量的销量预测

1.1.1 历史销量

早期关于销量预测的研究主要集中于使用时间序列分析方法，通过寻找销量数据过去的规律来预测其未来的发展趋势。李响等[1]通过自回归滑动平均模型（Auto-Regressive Moving Average Model，ARMA）与径向基函数（Radial Basis Function，RBF）神经网络相结合的混合模型来对销量进行了预测，并通过仿真试验验证了模型的有效性。王旭天等[2]考虑了季节性因素的影响，采用季节性差分自回归滑动平均模型（Seasonal Auto-Regressive Moving Average Model，SARIMA）并选取2004年到2015年的月度销量数据来进行销量预测。

1.1.2 宏观经济指标

在众多影响乘用车销量的因素中，宏观经济方面的因素是非常重要的外部因素。王栋等[3]通过灰色关联分析法筛选出国民总收入、人均国内生产总值（Gross Domestic Product, GDP）、进出口总额等7 个影响汽车保有量的相关因子，将其加入反向传播（Back Propagation, BP）神经网络模型进行预测分析。Gao等[4]分析了中国汽车销量与经济变量之间的关系，建模结果表明钢铁产量和汽油价格为内生变量，并与中国汽车销量之间存在长期协整关系，因此建立了向量误差修正模型（Vector Error Correction Model,VECM）来定量分析内生变量对中国汽车销量的长期影响。

1.1.3 网络搜索数据

网络搜索数据能够体现用户的关注意向和需求变化，可以提高销量预测模型的精准度。袁庆玉等[6]首先将关键词进行合成，之后建立模型研究关键词合成指数与汽车销量之间的关系并进行预测。李忆等[7]运用文本挖掘技术确定网络搜索关键词库，构建固定效应模型来研究网络搜索数据与汽车销量的关系，最终发现两者间存在长期均衡关系。

1.2 基于双类型变量的销量预测研究

现有研究中也有不少学者结合两种类型的变量对汽车销量进行建模预测。王易等[5]结合历史销量数据与宏观经济数据，建立了极端梯度提升（eXtreme Gradient Boosting，XGBOOST）模型对汽车销量进行了预测研究。Yong等[8]提出预测电动汽车量化市场需求的模型，考虑5 个经济指标和关键词“电动汽车”百度指数的外部影响，建立了多元向量自回归模型（Vector Autoregressive Model，VAR），使预测精度得到显著提高。刘吉华等[9]以大众汽车为研究对象，构建其网络搜索关键词库，并基于主成分分析将关键词进行合成，建立了结合历史销量数据与网络搜索数据的回归预测模型。刘吉华等[10]在以后的研究中还将深度学习的算法引入汽车销量预测，用卷积神经网络模型（Convolutional Neural Network，CNN）来对结合历史销量数据与网络搜索数据的大众汽车进行销量预测。

综上所述，可以发现目前对于汽车销量预测分析有很多效果良好的研究模型，但在变量的选择与组合方面，少有同时考虑历史销量、宏观经济指标和网络搜索数据作为自变量的研究，因此本文将在此基础上尝试逐步添加历史销量、宏观经济指标、网络搜索关键词，作为自变量建立多变量销量预测模型（Multivariate Sales Forecasting Model，MSFM）并进行效果比对分析。

2 基于梯度提升决策树的销量预测模型构建

本文首先进行变量选择与数据获取，然后对各变量数据进行如主成分分析和标准化等预处理，最后将各变量数据逐步加入梯度提升决策树算法进行训练，本文所构建的销量预测模型的框架如图1所示。

图1 销量预测模型构建框架

2.1 变量选择

本文将尝试在模型中逐步加入历史销量、宏观经济指标、网络搜索数据3 种变量进行建模。下面首先对这3方面的变量进行介绍。

2.1.1 历史销量

在时间序列数据的构成要素中，季节变动和循环变动都是序列数据随着季节的变化或者固定型周期而发生的有规律的周期性变动[11]，因此研究历史销量数据的规律变动能够从一定程度上预测未来销量数据的变化趋势。

2.1.2 宏观经济指标

乘用车行业深受经济因素变动的影响，经济因素大多体现一个国家的发展情况和人民的平均生活水平，一个国家经济水平越高，人民的生活水平越高，对乘用车的购买力就越强。本文选取了常用的消费者物价指数（Consumer Price Index, CPI）和92 号汽油价格作为影响乘用车销量的宏观经济指标变量[4,8,12]。

2.1.3 网络搜索关键词

近年来，随着互联网和大数据的发展，消费者们在购买商品之前越来越倾向于在网络上通过搜索引擎查找或咨询商品的相关信息和评价，以此为参考来做出进一步的消费行为。所以，网络搜索数据为商品市场发展动向和趋势提供了一定程度的前瞻。消费者在进行网络搜索时，通常会选择自己关注商品的关键词进行搜索，因此现有的网络搜索数据大都是根据搜索引擎中用户对于关键词的搜索量为基础形成的。比如百度指数是指互联网用户对关键词搜索关注程度及持续变化情况，其是以网民在百度的搜索量为数据基础，以关键词为统计对象，科学分析并计算出各个关键词在百度网页搜索中搜索频次的加权[13]。本文也选取百度指数作为销量预测中的自变量之一。

本文销量预测模型中所涉及的变量如表1所示。

表1 销量预测模型涉及变量

2.2 数据预处理

2.2.1 时间序列分解

一个时间序列通常由长期趋势、季节变动和不规则波动部分组成[14]。为了研究销量时间序列的规律变动，本文选择将时间序列进行分解来判断其季节变化周期。关于时间序列的分解模型主要分为加法模型和乘法模型，如公式（1）和公式（2）所示：

式中，Value为时间序列值；Trend为长期趋势值；Seasonal为季节变动值；Resid为不规则变动值。

加法模型中时间序列的各个组成成分是相互独立的，都有相同的量纲。而乘法模型中输出部分和趋势项有相同的量纲，季节项是比例数，不规则变动项为独立随机变量序列，服从正态分布。通过对时间序列进行分解能够快速找到时间序列的季节或周期变动规律。

2.2.2 时差关系分析

为了对关键词进行筛选，本文采取时差关系分析来研究关键词百度指数数据与乘用车销量之间的相关关系。时差关系分析是利用相关系数验证两组时间序列之间先行、一致或滞后关系的常用方法，其计算公式如公式（3）所示[15]：

式中，rl是两组时间序列的相关系数；l表示先行或滞后阶数，l取负数时表示先行，取正数时表示滞后。在经济预测领域，一般只考虑具有预测作用的先行关键词。

对于rl的取值，当rl＞0 时表示两组时间序列呈正相关；当rl＜0 时表示两组时间序列呈负相关。在相关程度上，当0 ＜ |rl|≤0.3 时认为两组时间序列不存在相关关系或相关性极弱；当0.3 ＜ |rl|≤0.5 时认为两组时间序列为低度线性相关；当0.5 ＜ |rl|≤0.8时认为两组时间序列为中度线性相关；当 |rl|＞0.8时认为两组时间序列为高度线性相关[16]。

2.2.3 主成分分析

由于网络搜索关键词数据多而复杂，且多个相关关键词的百度指数数据之间一般存在多重共线性，于是本文采取主成分分析的方法来对关键词进行合成，以消除数据间的多重共线性。主成分分析是一种利用降维的思想，通过正交变换将一组可能存在相关性的变量转换为一组线性不相关变量的统计方法，转换后的这组变量叫主成分[9]。主成分分析的主要步骤如下：

（1）指标转换

假设进行主成分回归的指标变量有m个，分别为X1,X2,…,Xm，共有n个样本数据，第i个样本的第j个指标的取值为aij。将各指标值aij转换成标准化指标值如公式（4）所示：

式中，uj，sj分别为第j个指标的样本均值和样本标准差。对应地称为标准化指标变量。如公式（5）所示：（2）计算相关系数矩阵

相关系数矩阵R= (rij)m*m，式中对角线元素rii= 1，rij=rji是第i个指标与第j个指标的相关系数，如公式（6）所示：

（3）计算特征值与特征向量

计算相关系数矩阵R的特征值λ1≥λ2≥… ≥λm≥0 时对应的特征向量μ1,μ2,…,μm，其中μj=[μ1j,μ2j,…,μmj]T，由特征向量组成m个新的指标变量，如公式（7）所示：

式中，Y1是第一个主成分；Y2是第二主成分；…，Ym是第m主成分。

（4）计算主成分贡献率及累计贡献率

根据公式（8）和公式（9），称bj为主成分Yj的信息贡献率，αp为主成分Y1,Y2,…,YP的累积贡献率，当αp接近于1 时，则选择前p个指标变量Y1,Y2,…,YP作为p个主成分，代替原来m个指标变量，从而可对p个主成分进行综合分析(p≤m)。

2.2.4 数据标准化

本文选取使用的梯度提升决策树（Gradient Boosting Decision Tree, GDBT）算法与梯度有关，为了避免预测结果向数值大的变量倾斜，需要对数据进行标准化处理，如公式（10）所示[17]：

2.3 模型训练与结果分析

2.3.1 数据集划分

机器学习算法在训练前一般需要将数据集划分成独立的3部分，即训练集、测试集和验证集。其中训练集用于训练模型，验证集用于评估模型，协助调整模型超参数，测试集则是用于检验最终选择的最优模型的性能表现。

2.3.2 梯度提升决策树

梯度提升决策树算法可以灵活处理各种类型的数据，且其模型一般具有较好的解释性和鲁棒性，因此本文选择梯度提升决策树算法为基础来进行乘用车销量预测研究。

梯度提升决策树（GDBT）是Friedman在2001年提出的一种迭代学习的决策树算法[18]。GDBT 采用的是集成学习中Boosting 算法的基本思想，即首先使用初始权重从训练集中训练出一个弱学习器，根据弱学习器的学习误差率来更新样本的权重，提高之前弱学习器学习率较高的训练样本点权重，使得这些误差率高的样本在后面的弱学习器中得到更多的重视。如此循环，直到得到指定数量的学习器，再结合策略进行式就是各棵决策树。总体上，GBDT 是通过采用加法模型（即基函数的线性组合）以及不断减小训练过程产生的残差来达到将数据分类或者回归的算法。

2.3.3 结果比对分析

为了验证各个变量对销量预测的影响，本文在GDBT算法基础上，分别构建只考虑历史销量的模型1，同时考虑历史销量和宏观经济指标的模型2，同时考虑历史销量、宏观经济指标和网络搜索关键词的模型3来进行训练（如式（11）至式（13）所示）并进行结果比对分析。

3 实证研究与结果分析

3.1 数据获取与预处理

3.1.1 销量数据

本文从车主之家官网获取了乘用车市场2013 年1 月至2021 年12 月共72 个月的销量数据，其时序图如图2所示。在模型评价指标的选择上，由于平均绝对百分误差（Mean Absolute Percentage Error，MAPE）数值是百分比的形式，更能形象地表达出误差值，易于解释，因此本文选取MAPE 来对不同模型进行效果比较[19]，其计算公式如公式（14）所示：

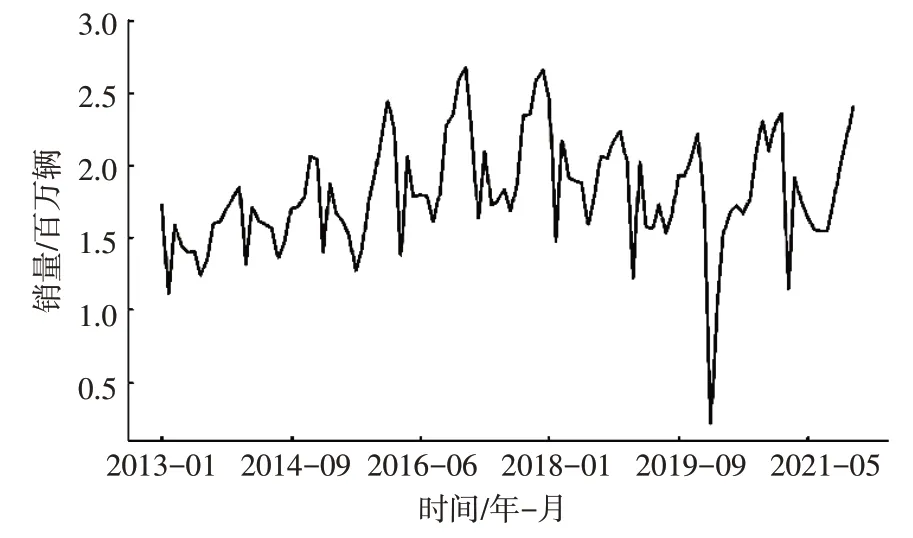
图2 乘用车销量时序图

式中，yi是t时刻的预测值；yi是t时刻的真实值。理论上，MAPE 的值越小，说明预测模型拟合效果越好，具有更好的精确度。

由图2所展示的时序图可以初步认为乘用车的月度销量数据有一定的周期性变化，接下来对其进行分解来判断其季节变化周期。本文采用Python的statesmodel 库中的seasonal_decompose 函数来对乘用车的销量数据进行时间序列分解，加法模型和乘法模型的结果分别如图3、图4所示。

图3 乘用车销量序列分解（加法模型）

图4 乘用车销量序列分解（乘法模型）

由图3 和图4 所展示的时间序列分解结果可知，乘用车销量数据的季节变化周期均为12个月，故选择将去年同期的销量数据作为模型中的变量之一。

3.1.2 宏观经济数据

本文从东方财富网上通过网络爬虫获取了2014年1月至2021年12月的宏观经济数据，包括消费者物价指数（CPI）和92号汽油价格，其部分数据如表2所示。

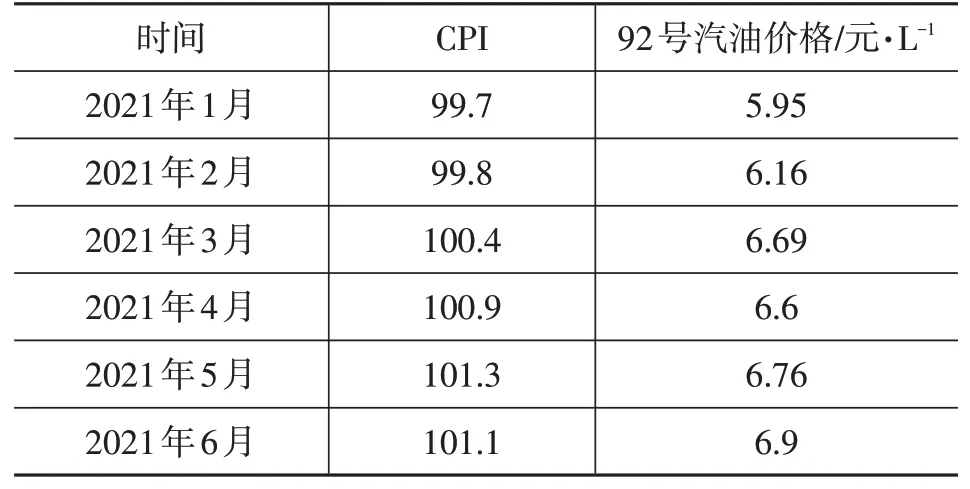
表2 宏观经济样本数据表（部分数据）

3.1.3 网络搜索关键词数据

由于受到不同消费者的语言习惯、搜索风格主观因素的影响，网络搜索关键词库变得庞大而复杂，因此构建合适的关键词组就成了研究的关键。

（1）关键词的获取

本文首先分别以“乘用车”作为初始核心关键词，然后利用百度指数需求图谱与相关词热度模块来进行两轮关键词的拓展，同时去除搜索指数较低以及明显与乘用车无显著关系的关键词，最终得到的关键词为86个，之后再根据选取的关键词在百度指数官网上通过网络爬虫获取到百度指数数值。采集到的部分数据如表3所示。

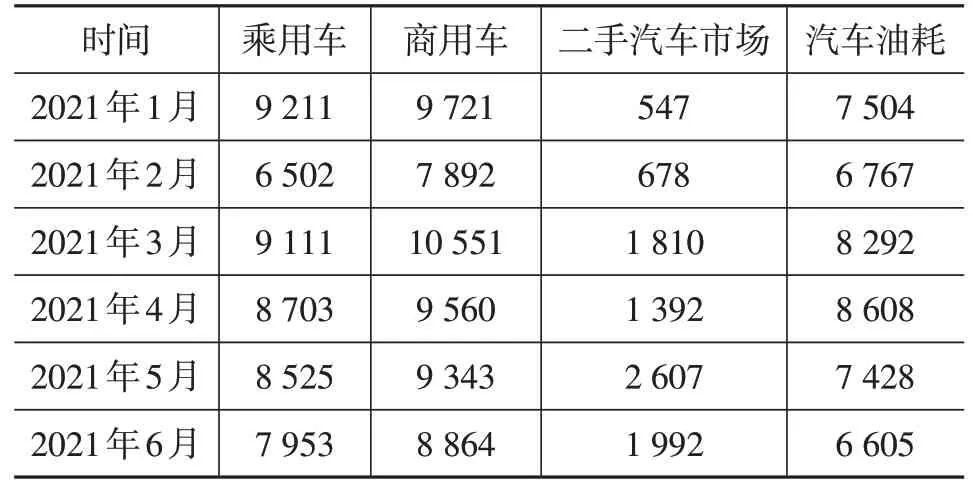
表3 网络搜索关键词百度指数数据表（部分数据）

（2）关键词的筛选

本文采取时差关系分析来研究关键词百度指数数据与乘用车销量之间的相关关系，从而对关键词进行筛选。首先取l∈[-6,0)（即先行阶数取1 至6），在每个关键词百度指数数据中选择相关程度为低度相关及以上（即相关系数 |rl|＞0.3）且相关系数值最大的先行阶数[16]，最终筛选得到的关键词为23 个，部分结果如表4所示。

表4 关键词百度指数数据时差关系分析结果（部分数据）

根据时差关系分析结果，将关键词按照先行阶数与销量数据进行对应，得到关键词筛选后的百度指数数据。

（3）关键词的合成

将经过预处理的百度指数数据运用Python 的sklearn库中的PCA()函数进行主成分分析，结果如表5所示。

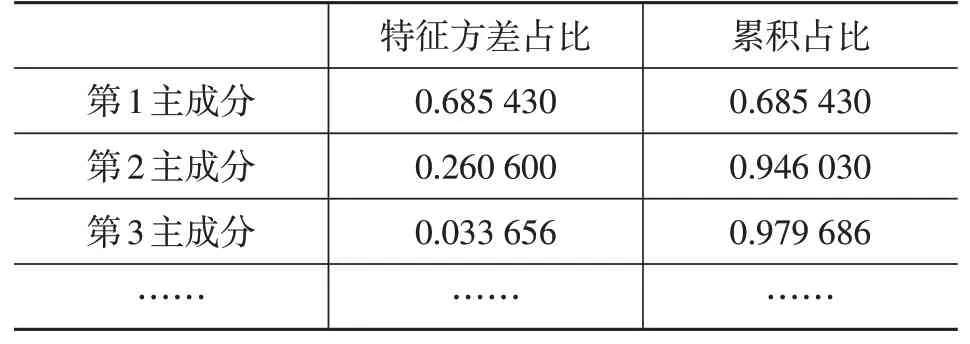
表5 百度指数数据主成分分析结果

由表5的结果可以得出，经过主成分分析降维后，前3个主成分的特征方差累计占比超过95%，包含了原数据的大部分信息，因此考虑将百度指数数据降维到3维。

3.1.4 数据标准化

本文使用Python的sklearn库中的StandardScaler()函数对以上获取并预处理过的销量数据、宏观经济数据和百度指数数据进行标准化处理。

3.2 模型训练

对于数据集的划分，本文选取2014年1月至2020年12月的数据作为训练集和验证集，选取2021年1月至12月的数据作为测试集。

模型训练方面，本文使用Python的sklearn库中的GradientBoostingRegressor()函数进行GDBT 算法的建模。对于模型中的超参数选择，选择用网格搜索的方法进行确定，即在指定的参数范围内，按步长依次调整参数，利用调整的参数训练学习器，从所有的参数中找到在验证集上精度最高的参数[20]。同时考虑到不同验证集对模型结果的影响不同，对训练集和验证集采取7折交叉验证的方式进行建模。本文使用sklearn库中的GridSearchCV()函数遍历多种超参数组合并通过交叉验证确定最优效果参数。

3.3 模型结果比对分析

在GDBT算法中逐步加入历史销量数据、宏观经济数据、网络搜索关键词数据所得到的各模型对乘用车2021年1月至12月的预测结果MAPE指标如表6所示。

表6 GDBT模型预测的MAPE指标结果

由表6 所展示的预测结果可知，只使用历史销量数据进行建模时，模型MAPE值为14.37%。添加了宏观经济指标进行建模后，MAPE 值有所降低，为12.71%，说明宏观经济指标对销量有一定的影响。当在模型中同时考虑历史销量、宏观经济指标和网络搜索关键词变量时，MAPE值进一步降低，模型效果进一步提升，表明了网络搜索数据有助于乘用车销量的预测。

在时间序列的相关预测问题中，季节性差分自回归滑动平均模型（Seasonal Auto-Regressive Moving Average Model，SARIMA）、支持向量机回归（Support Vector Regression，SVR）模型也得到了广泛应用[2,21]，为了证明本文所使用模型的有效性，进一步对比了同时考虑3 个变量时GDBT 模型与SARIMA 模型、SVR 模型的预测结果MAPE指标，结果如表7所示。

表7 不同模型预测的MAPE对比%

由表7可知，GDBT 模型的MAPE 指标比SARIMA模型、SVR模型都低，表明GDBT模型的拟合效果最优。

综合上述分析可以得出，同时使用历史销量、宏观经济指标、网络关键词搜索数据变量会使销量预测模型的精度提高，本文中得到的最优模型是GDBT模型，其MAPE值结果为10.35%，能够较好的预测销量变化。

4 结论与展望

4.1 研究结论

本文以乘用车整体市场为研究对象，在现有研究的基础上分别建立了只考虑历史销量的预测模型，同时考虑历史销量和宏观经济指标的预测模型，同时考虑历史销量、宏观经济指标和网络搜索关键词的预测模型，最终将建立的模型进行对比分析，发现同时考虑了3 种变量的梯度提升决策树模型的MAPE 值最小，说明其拟合效果最好，也表明了宏观经济指标和网络搜索数据有助于乘用车销量预测。

本文在理论层面以乘用车整体市场为研究对象，使用历史销量、宏观经济指标和网络搜索关键词数据作为影响乘用车销量的变量，得出同时使用上述3种变量的梯度提升决策树模型为最佳模型，为销量预测的研究提供一种新的参考模型。在实践层面，对于乘用车市场中已有一定渗透率的企业，可以基于本文得出的最优销量模型对市场趋势发展情况做参考，从而进行针对性的生产计划安排与优化以及市场营销战略的制定。