基于LESO的改进滑模磁悬浮控制算法
2023-12-04唐阳,杨杰
唐 阳,杨 杰
(1.江西理工大学 永磁磁浮技术与轨道交通研究院, 江西 赣州 341000; 2.江西省磁浮技术重点研究室, 江西 赣州 341000)
0 引言
磁悬浮控制系统是典型的非线性、时滞性、强耦合对象,现役磁浮列车通常基于传统PID控制[1]算法进行分段线性化等处理,能够满足常规运行环境的基本需求。但是当系统受到较大扰动或者系统内部参数摄动时,系统动态性能会迅速下降,甚至导致系统掉点、砸轨等现象。近年来,针对传统PID控制器在控制领域的不足,国内外学者做了大量研究,现代控制理论被广泛应用于磁悬浮控制系统中,如LQR控制器[2]、自适应控制器[3]、自抗扰控制器[4]等,更多的是采用智能控制和传统控制算法相结合的融合控制方法,如模糊PID控制[5]、PSO自抗扰控制[6]、神经网络PID控制[7]等。其中滑模变结构控制算法[8]响应速度快、系统在受到参数摄动和外干扰的时候具有“不变性”、对器件要求不高等特性,使得其逐渐受到各国学者的广泛重视。
滑模控制器由于具有较强的鲁棒性和抗干扰性能,所以在磁悬浮平台领域的应用值得被探索。文献[9]采用新型趋近律滑模算法和改进ESO相结合,提高混合悬浮系统鲁棒性和使得系统无抖振,有更好的跟踪性能。文献[10]将滑模控制引入到误差反馈控制律中,实现了磁悬浮轴承多自由度解耦控制,加快响应速度,增强抗干扰能力。文献[11]采用一种滑模观测器的模型预测控制方法,使得磁悬浮球系统的动态性能得到显著的改善,并且通过将观测到的系统内部参数摄动和外界扰动及时反馈到控制器,进一步提升系统的鲁棒性和抗干扰性。文献[12]针对磁悬浮球系统存在严重非线性和不确定性问题,提出了一种分数阶滑模控制,不仅使得磁悬浮球具有较好的跟踪性能,而且对系统的不确定性具有较强的鲁棒性。文献[13]针对陀螺转子高速旋转时产生的不平衡振动,采用滑模观测器与自适应控制策略相结合,消除不平衡抖振且适用于主被动磁悬浮转子。文献[14]针对磁悬浮小车非线性、时变性的控制问题,采用一种变论域自适应模糊滑模-PID混合控制策略,消除滑模抖振现象以及增强系统鲁棒性。文献[15]为实现磁悬浮平台气隙的精确控制,采用模糊滑模控制方案,实现高刚度稳定悬浮,具有很强的鲁棒性。
滑模变结构控制算法应用在磁悬浮技术领域具有可行性,但是一般滑模变结构控制的抖振问题是该控制算法研究的重难点。本文中采用LESO观测器[16]对系统的悬浮间隙,悬浮间隙变化量和系统总扰动量进行观测,既可以缓和滑模变结构控制对系统参数的依赖,又可以将总扰动量补偿给滑模控制器中;理论上,LESO对系统扰动能够更加准确、快速的跟踪曲线,整个系统的抗干扰能力越强。另外,本文中结合等速趋近律,变速趋近律等[17]不同趋近律算法,分析滑模控制产生抖振的本质,从而通过控制系统抖振的频率和幅值,使得抖振在合理的范围内波动,最终实现具有工程实际意义的磁悬浮控制。
1 系统建模
1.1 数学建模
为了更好的研究悬浮系统的性能,将其简化为F轨电磁悬浮系统模型如图1所示,该系统的工作原理:根据实际控制量电压的变化,不断调节流经电磁铁的电流大小使得电磁吸力能过够满足悬浮要求,最终实现电磁铁能够稳定悬浮。
由图1可知,F轨悬浮系统的数学模型可以描述如式(1):
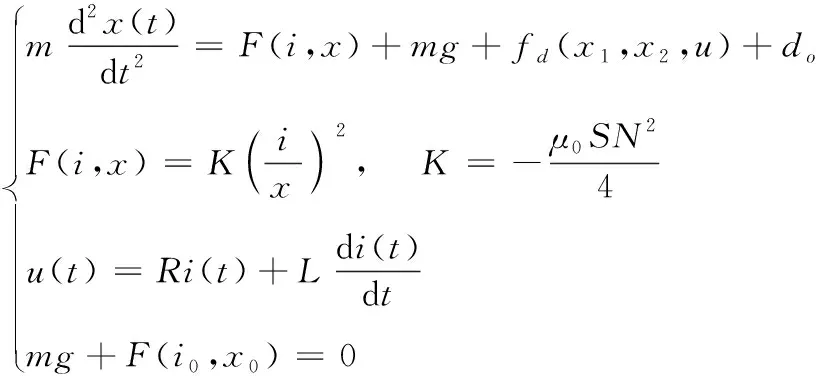
(1)
式(1)中:选择F轨重力方向为正参考方向;i(t)表示励磁线圈电流;x表示F轨距上梁距离;F(i,x)表示电磁吸力;F(i0,x0)表示平衡位置的电磁吸力;u(t)表示电磁铁绕组的两端电压;fd(x1,x2,u)为系统内部扰动;do为系统外部扰动,系统模型物理参数如表1所示。
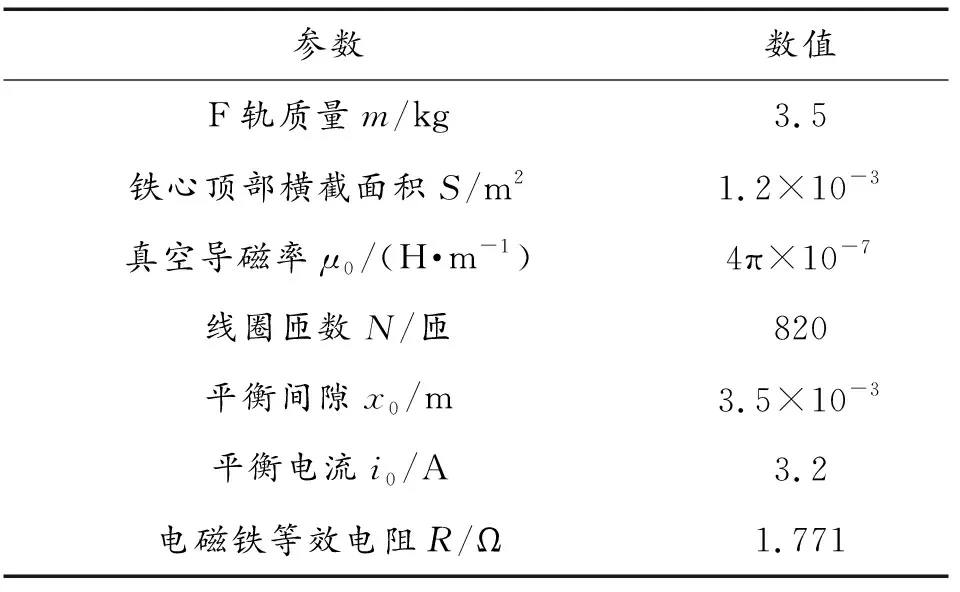
表1 F轨悬浮平台物理参数
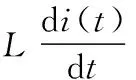
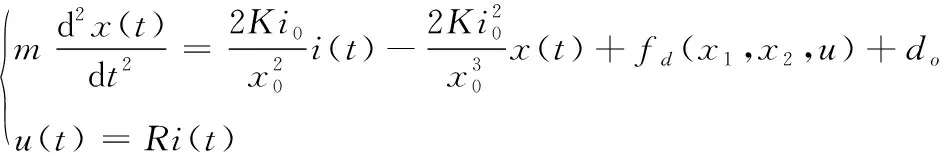
(2)
对式(2)进行拉普拉斯变换如式(3):

(3)
将表1的数据代入式(3)可得如式(4):
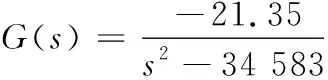
(4)
1.2 系统问题描述
由上述的数学模型可知,该传递函数是非线性不稳定系统,传统的控制策略满足不了控制需求,本文中采用滑模变结构控制策略。
根据现有的理论,在仿真试验中,验证了一般滑模变结构控制具有滑动模态上的“不变性”,如图2所示。
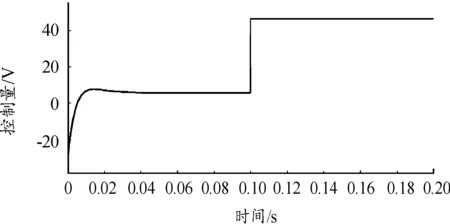
图2 滑模控制仿真图Fig.2 Sliding mode control simulation diagram
即当系统状态处于滑动模态时,若外界干扰和内部参数摄动能够及时反馈到控制器中,则控制器能够有效的抑制甚至消除其给系统带来的影响,进而可以提高悬浮系统的抗干扰性能和鲁棒性,且该算法存在过度依赖系统参数问题;因此,本文中采用一种具有跟踪速度较快,参数整定简单的线性扩张状态观测器,将提高系统的动态性能。
结合系统中存在不确定性和未知扰动,将简化系统状态空间方程如式(5):
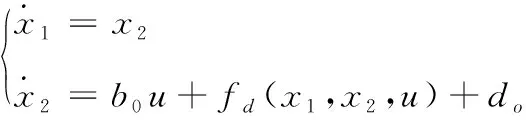
(5)
2 基于LESO的改进趋近律滑模控制
2.1 磁悬浮系统的LESO设计
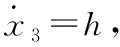
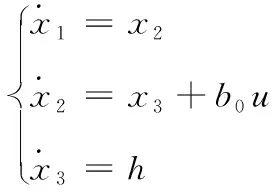
(6)
定义观测器增益矩阵为L=[β1,β2,β3]T,对这个系统建立状态观测器,得如式(7):
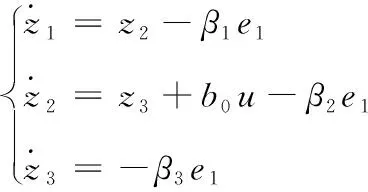
(7)
式(7)中:z1、z2、z3分别为x1、x2、x3的观测值,将观测器式(6)和被控对象式(7)联立得出,扩张状态观测器的误差方程为e1=z1-x1,e2=z2-x2,e3=z3-x3,则有:
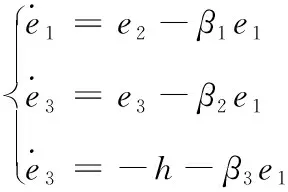
(8)
其中式(8)可以描述为如式(9):

(9)
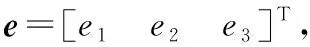
det(λI-A)=λ3+β1λ2+β2λ+β3
(10)
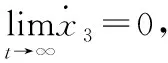
为了减少参数的调整,采用高志强教授提出的基于带宽法的LESO[18]如式(11):
det(λI-A)=(s+ωo)3
(11)
即如式(12):
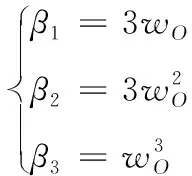
(12)
通过配置参数wo即可以将系极点全部拉回s平面的左半平面,使得线性扩张状态观测器能够稳定的跟踪着扰动量。
2.2 控制算法设计
传统一般滑模变结构控制算法以现代控制理论基础,在系统状态空间中构建滑模面函数,一般为一阶线性函数,滑模面S将状态空间分成上下两部分,状态变量在空间任意一点的运动过程分为趋近运动和滑模运动。如图3所示,状态变量从初始点a出发,向靠近滑模面S的方向运动,此时,该的运动过程为趋近运动;在满足一定条件下,状态变量会被“吸引”到达S超平面附近点b,状态变量进入滑模运动过程,沿着滑模面做趋近原点o的运动,最终稳定收敛于原点。
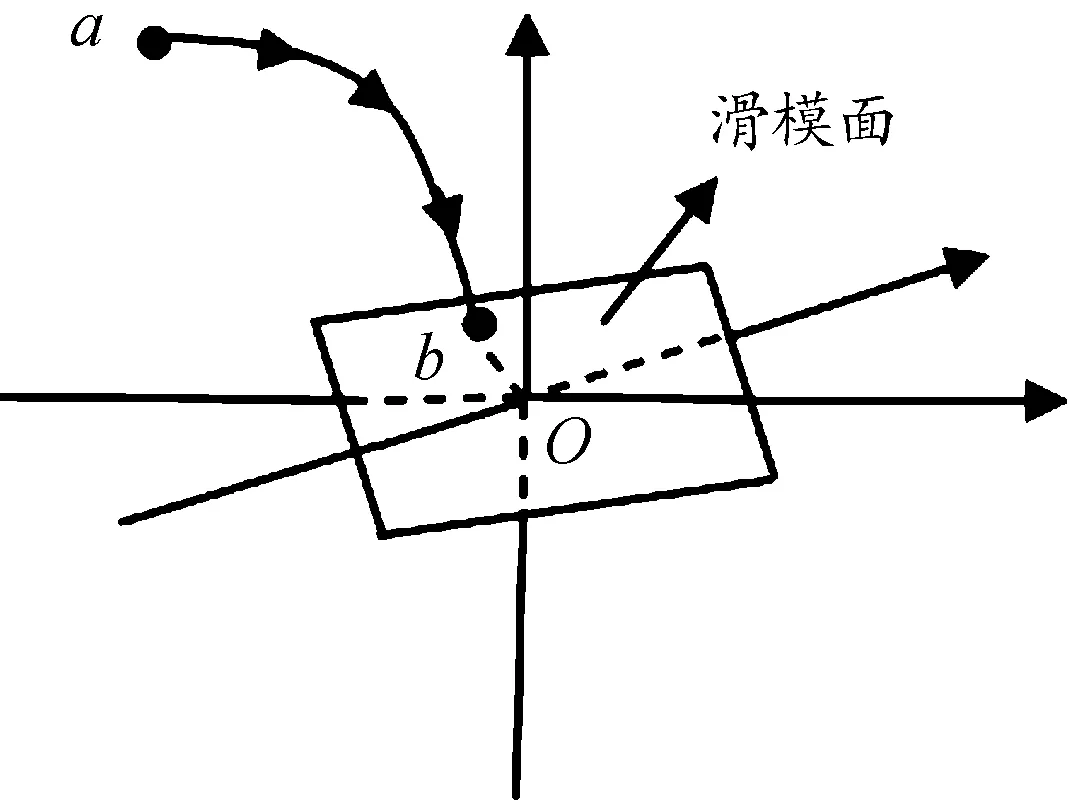
图3 滑模控制原理Fig.3 Sliding mode control principle
为满足上述运动过程,需使如式(13)
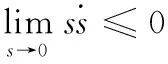
(13)
一般的滑模变结构控制[19]仅要求系统状态能够趋近滑模面并稳定收敛于原点,不能很好的反应其整个运动过程,且其稳定条件是求解不等式的函数,解法复杂;而高为炳教授提出的趋近律法滑模控制[20],能够在加快响应速件下,有效的抑制抖振,并且简化的控制器u的计算步骤。
根据式(4),可以构建出系统误差方程如式(14):
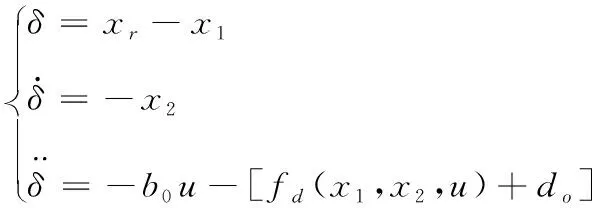
(14)
由于实际系统中状态变量很难实现准确测量,即采用扩张状态观测器的观测值代替系统状态变量实际值,即可以缓和滑模控制对参数依赖程度,分别取x1=z1,x2=z2,x3=z3=fd(z1,z2,u)+do,式(15)如下:
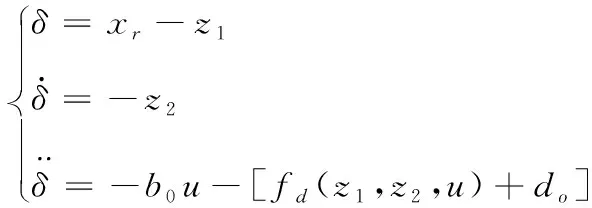
(15)
本文中采用线性滑模面,其如式(16)所示:

(16)
为了提高滑模控制的动态品质,引入了趋近律概念,其中等速趋近律如式(17)所示:
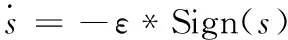
(17)
等速趋近律可以在有限的时间内到达滑模面,当状态变量进入滑动模态时,由于符号函数Sign使得系统状态围绕滑模面不断抖振;当系统减弱抖振时,响应速度会变慢,抗干扰性能会大幅度减小。为了在减弱抖振条件下,保持其他动态性能,需要重新设计一种改进趋近律算法。
为克服上述等速趋近律的缺点,提出了一种改进趋近律如式(18):
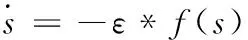
(18)
为了削弱系统抖振频率,引入边界层可变的分段幂函数如式(19):
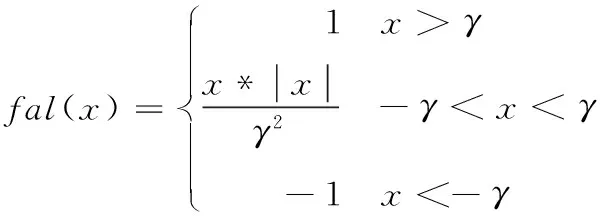
(19)
分段幂函数的特性曲线如图4所示。
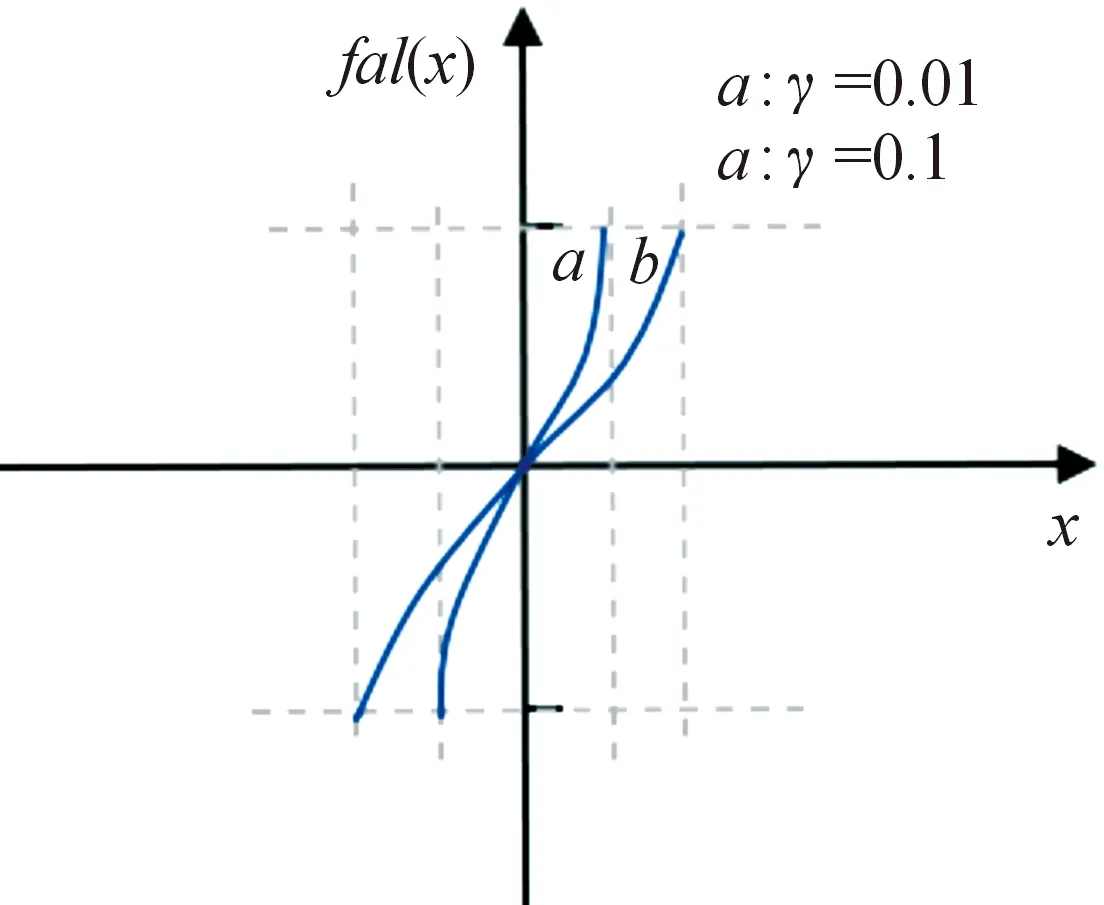
图4 分段幂函数特征曲线Fig.4 Characteristic curves of the power-of-part function
可以看出,当系统状态在远离S超平面,采用符号函数控制,保持系统状态原来的趋近速率;当系统状态接近S超平面时,采用连续幂函数控制,削弱了由于符号函数自身函数特性带来的高频抖振,也可以合理的控制滑动模态的运动过程。通过改变γ的值,当γ越大时,能够更加缓和使状态变量进入S超平面,但是会引起系统的响应速度减慢;而当γ减小时,虽加快了响应速度,但会使得状态变量在进入S超平面抖振频率增大。因此根据系统特性选取合适的γ,可以更加精细的控制抖振频率,使得系统动态性能很好的提升。
为了进一步削弱抖振幅值,将滑模增益和S超平面进行联立如式(20)所示:

(20)
当系统状态远离超平面时,|s|>>1,增加滑模增益ε,使得系统状态能够更快的趋近滑模面,当系统状态接近超平面时,|s|<<1,减小滑模增益ε,削减系统状态由于滑模增益过大导致的抖振幅值问题。
上述2种削弱抖振的方法分别从抖振频率和抖振幅值2个方面控制,最终可以调节出系统最优的动态性能。结合上式,得出如式(21)所示:
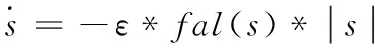
(21)
联立式(15)和式(21),得到滑模控制律为如式(22)所示:
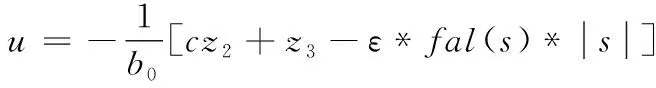
(22)
其中z3=fd(z1,z2,u)+do,该部分为总扰动观测值,该观测值的跟踪性能对于滑模控制器中抗干扰性能和鲁棒性起着决定性作用,采用一般的LESO足够很好的满足跟踪性能。
2.3 稳定性分析
基于LESO的改进滑模控制器的稳定性分析,其跟踪误差需要有界稳定的,取Lyapunov函数为如式(23)所示:
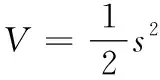
(23)
对其进行微分如式(24)所示:
-s*ε*fal(s)*|s|<-s*fal(s)<0
(24)
其中:s、fal(s)同号,ε>0;由式(24)可知,根据李雅普诺夫稳定判据,当LESO可以有效跟踪系统状态变量和系统扰动时,即LESO与控制系统构成的串联积分型稳定时,改进滑模控制跟踪系统误差是有界、稳定的。
基于LESO的改进滑模控制器原理图整体如图5所示,将LESO与控制系统构成的串联积分型,在通过改进的滑模控制律来控制串联积分系统,LESO的快速跟踪效果可以很好的与滑模控制中的“不变性”本质有机结合,从而使得系统的抗干扰性和鲁棒性进一步提升。
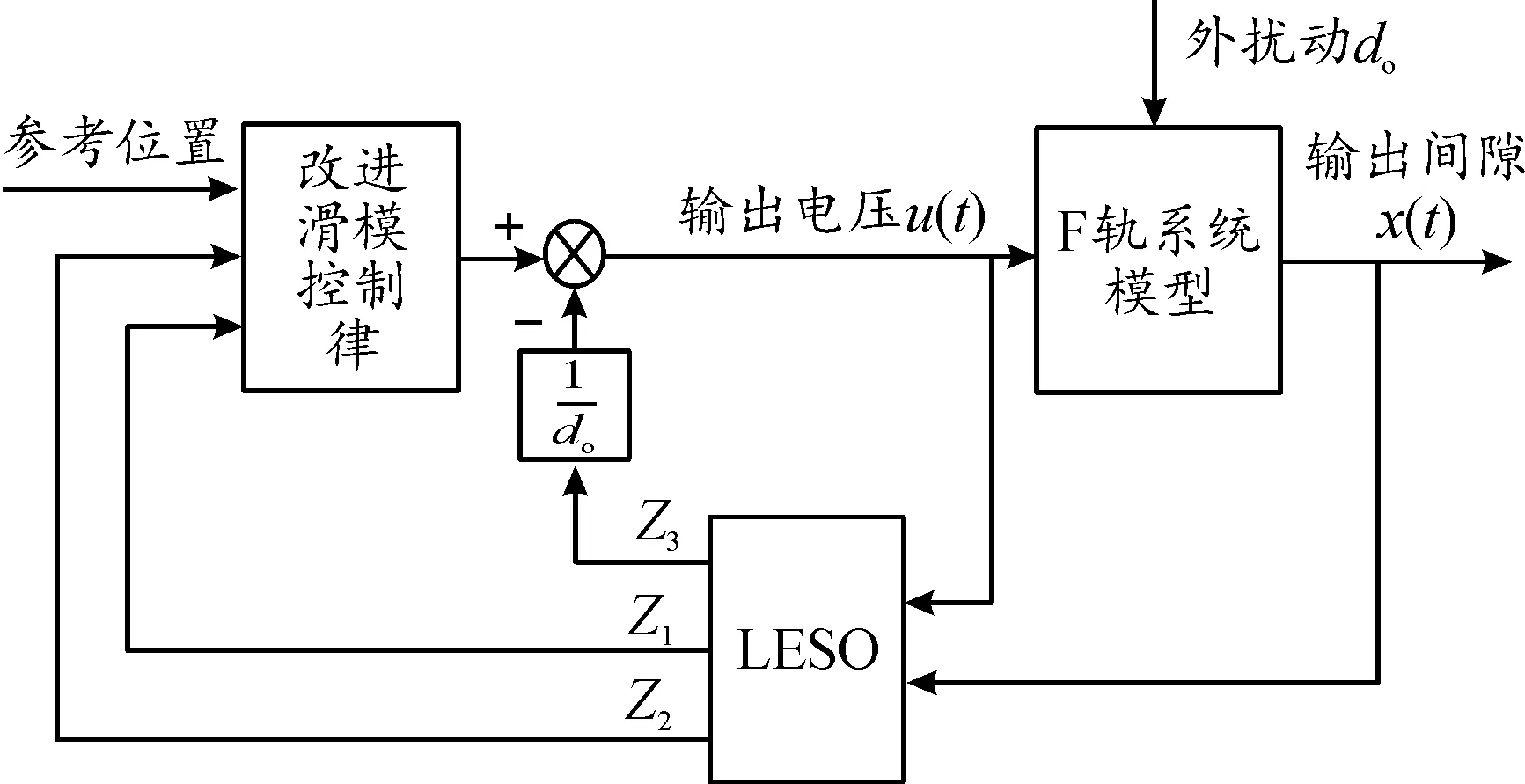
图5 基于LESO的改进滑模控制原理Fig.5 Improved sliding mode control principle based on LESO
3 仿真分析
本文中利用Simulink仿真软件对悬浮系统进行仿真,初始时预设3.5 mm的悬浮间隙,为了与基于LESO的改进滑模控制效果做对比,还设计了PID控制器和等速控制器,其中PID参数最好的一组为P=-8 120,I=-3 231 000,D=-394;
为验证基于LESO的改进滑模控制器的优越性,仿真设计方案如下:
1) 阶跃响应实验,在无扰动状态下,将基于LESO的改进滑模控制与PID控制和等速滑模控制进行对比;
2) 抗干扰性实验,在0.4 s和0. 7 s时刻,同时突加一个的外界负载扰动,比较基于LESO的改进滑模控制与PID控制的抗干扰能力;
3) 跟随性实验,通过改变给定的间隙信号,使系统跟踪2.5 mm与4.5 mm悬浮间隙,对比观察2种基于LESO的改进滑模控制与PID控制的跟随性能;
4) 鲁棒性实验,根据系统的实际运行过程中,可能受到因自身故障导致系统状态偏离原定值,通过改变b值,分析对比基于LESO的改进滑模控制与PID控制的跟随性能;
① 阶跃响应实验。在Simulink仿真环境下,观察PID控制、等速滑模控制与基于LESO改进滑模控制响应情况,仿真结果如图6所示。
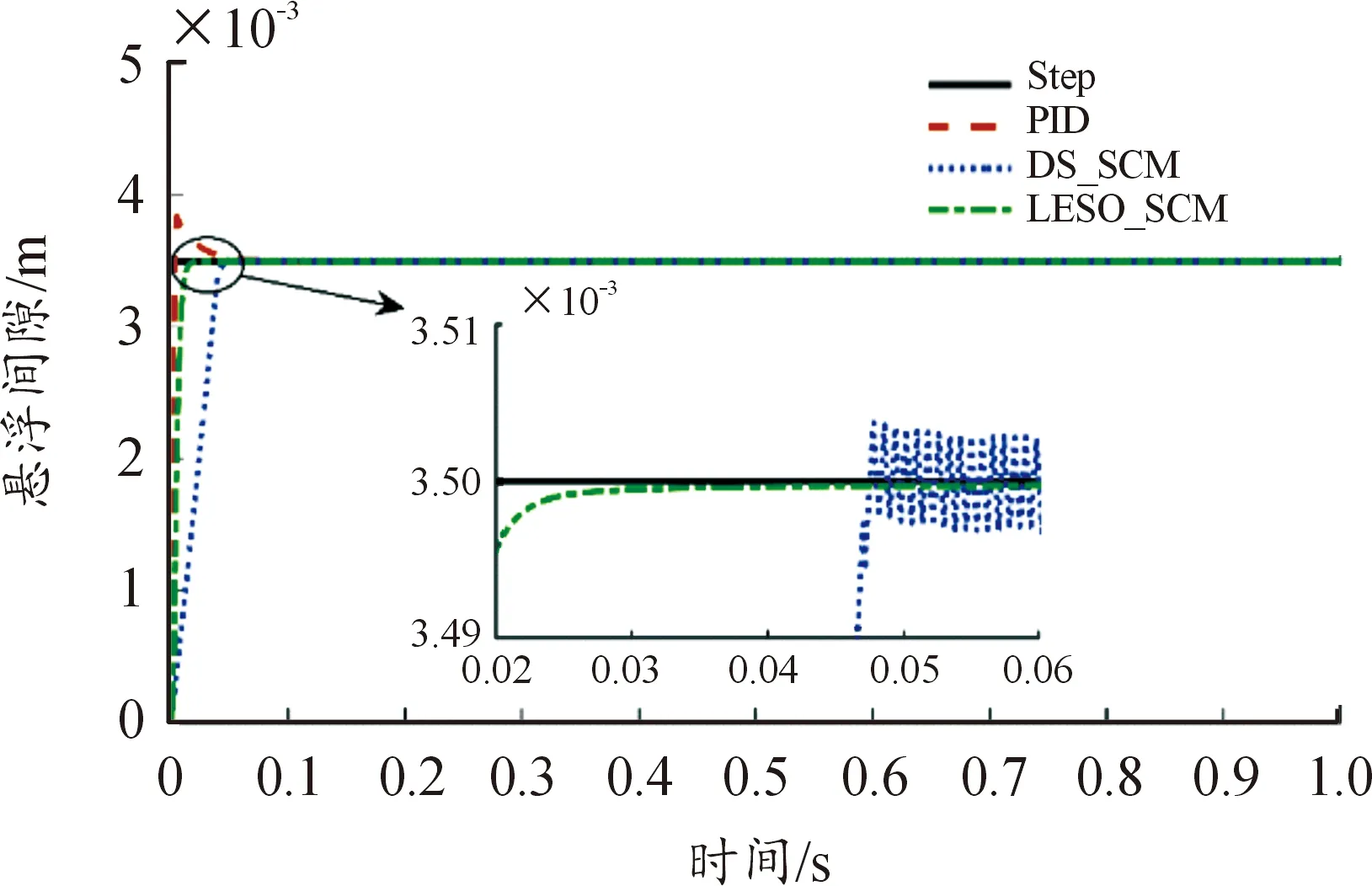
图6 定间隙阶跃响应曲线Fig.6 Fixed-gap step response curve
由图6可知,在给定间隙3.5 mm情况下,PID、等速滑模控制与基于LESO的改进滑模控制都可以短时间内达到稳定状态,PID控制的响应时间为0.1 s且最大超调量为9.7%,而等速滑模算法既可以在0.05 s内跟踪响应且几乎没有超调,有效处理了PID控制响应时间和超调量的矛盾;由于等速滑模控制存在的抖振势必影响实际系统的稳定性,采用基于LESO改进滑模控制,在继承等速滑模控制优越性的条件下,响应时间为0.025 s且最大程度上削弱抖振。
② 抗干扰性实验。在0.4 s时刻同时给系统突加100 N的阶跃负载干扰,观察其抗干扰能力,仿真结果如图7所示。
由图7可知,在0.4 s时突加100 N负载扰动时,3种控制算法都能重新达到稳定状态,但是等速滑模控制,会出现明显的稳态静差,即不做比较分析。此时,PID算法的最大间隙变化量为0.016 mm,是基于LESO改进滑模控制的0.003 mm的5倍多,并且PID控制恢复稳定的时间为0.08 s,而基于LESO改进滑模控制却只需要0.012 s,体现出滑模变结构控制抗干扰性能强。
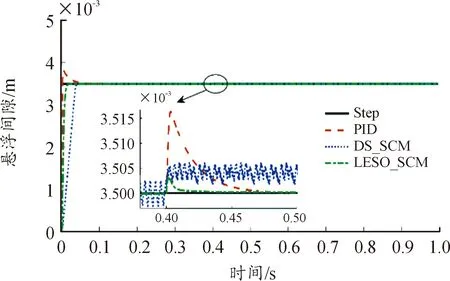
图7 阶跃小负载干扰曲线Fig 7 Step small load interference curve
为进一步验证滑模变结构控制的抗干扰性能,在0.7 s时刻给系统突加1 000 N的大负载干扰,观察其抗干扰能力,仿真结果如图8所示。
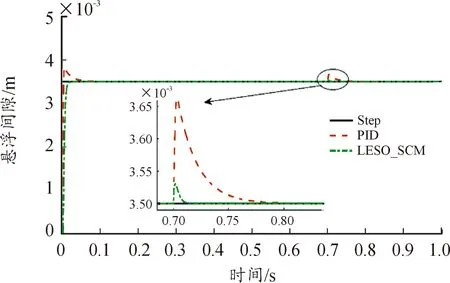
图8 阶跃大负载干扰曲线Fig 8 Step large load interference curve
由图8分析可知,在0.7 s时1 000 N负载扰动时,其中PID控制和基于LESO的改进滑模控制可以重新稳定,而等速滑模控制,会出现严重的发散现象。
为了更好的体现基于LESO改进的滑模控制在抗干扰性能的优越性,对比悬浮系统在不同扰动条件下的数据,如表2所示。

表2 扰动性能对比
在等幅增大扰动情况下,PID控制和基于LESO的改进滑模控制的恢复稳态的时间和最大间隙变化量,出现不同比例变化,PID控制的性能指标的数值增幅比值相比基于LESO的改进滑模控制大,从而体现出基于LESO的改进滑模控制抗干扰性能的优越性。
综上所述,LESO改进滑模算法即消除等速滑模算法的稳态误差,又改善了其在大扰动情况下发散的现象,与PID算法相比,进一步提高系统的抗干扰性能。
③ 跟随性实验。考虑中低速磁悬浮列车的轨道面的不平整性,而导致列车悬浮间隙出现的波动,因此研究基于LESO的改进滑模控制与PID控制对变间隙的跟随能力很有必要。通过仿真,观测比较不同悬浮间隙,具体设置如下:在0.4 s时,给定为2.5 mm与4.5 mm的方波间隙信号,对比2种算法的跟踪性能,仿真结果如图9所示。
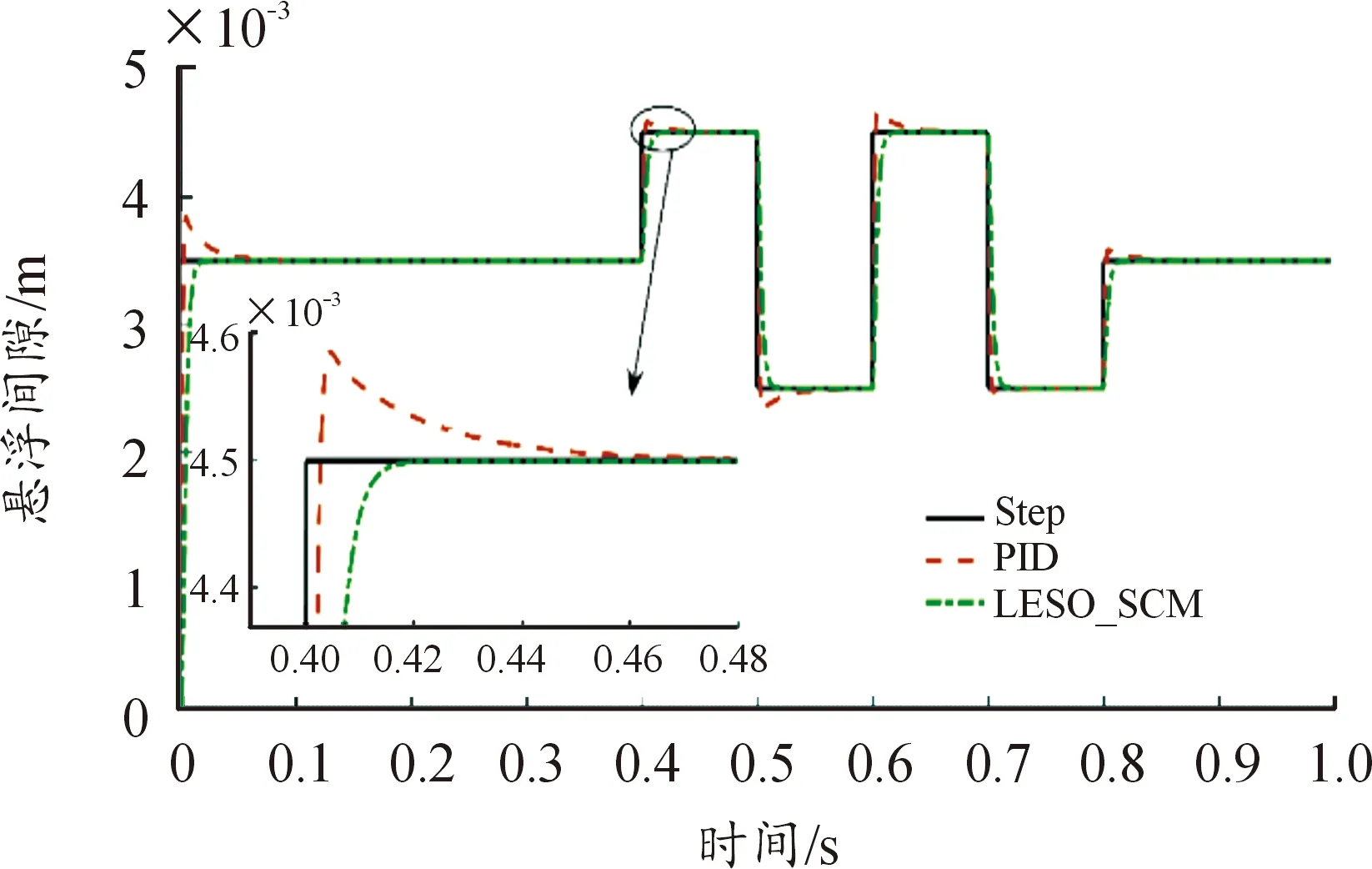
图9 跟随响应曲线Fig.9 Follow the response curve
从仿真结果可以得出,当悬浮间隙发生变化时,PID控制存在较大的超调量且响应速度较慢。从0.4 s时刻起每一次悬浮间隙跳跃变化,PID控制都会出现超调,而基于LESO的改进滑模控制几乎没有超调,PID控制响应时间是基于LESO的改进滑模控制的4倍,这意味着基于LESO的改进滑模控制具备有良好的适应性和跟随性,优于PID控制。
④ 鲁棒性实验。当系统在正常运行的条件下,由于内在参数摄动导致系统发生变化,其中控制量系数b变化对系统稳定性影响最为明显,所以将系统参数b设置为-15、-10、-5,观测2种算法的跟踪性能,仿真结果如图10所示。
由仿真结果可得出以下结论,当模型参数b由于摄动逐渐偏离原定值b=-21.35时,基于LESO的改进滑模控制表现出更加稳定性能跟踪,其响应时间和超调量波动并不明显;根据抗干扰性能仿真可知,基于LESO的改进滑模控制相比PID控制当参数摄动大即b=-5,PID控制会出现发散的现象,而基于LESO的改进滑模控制仍然能逐渐稳定,具有更加可靠的稳定性。
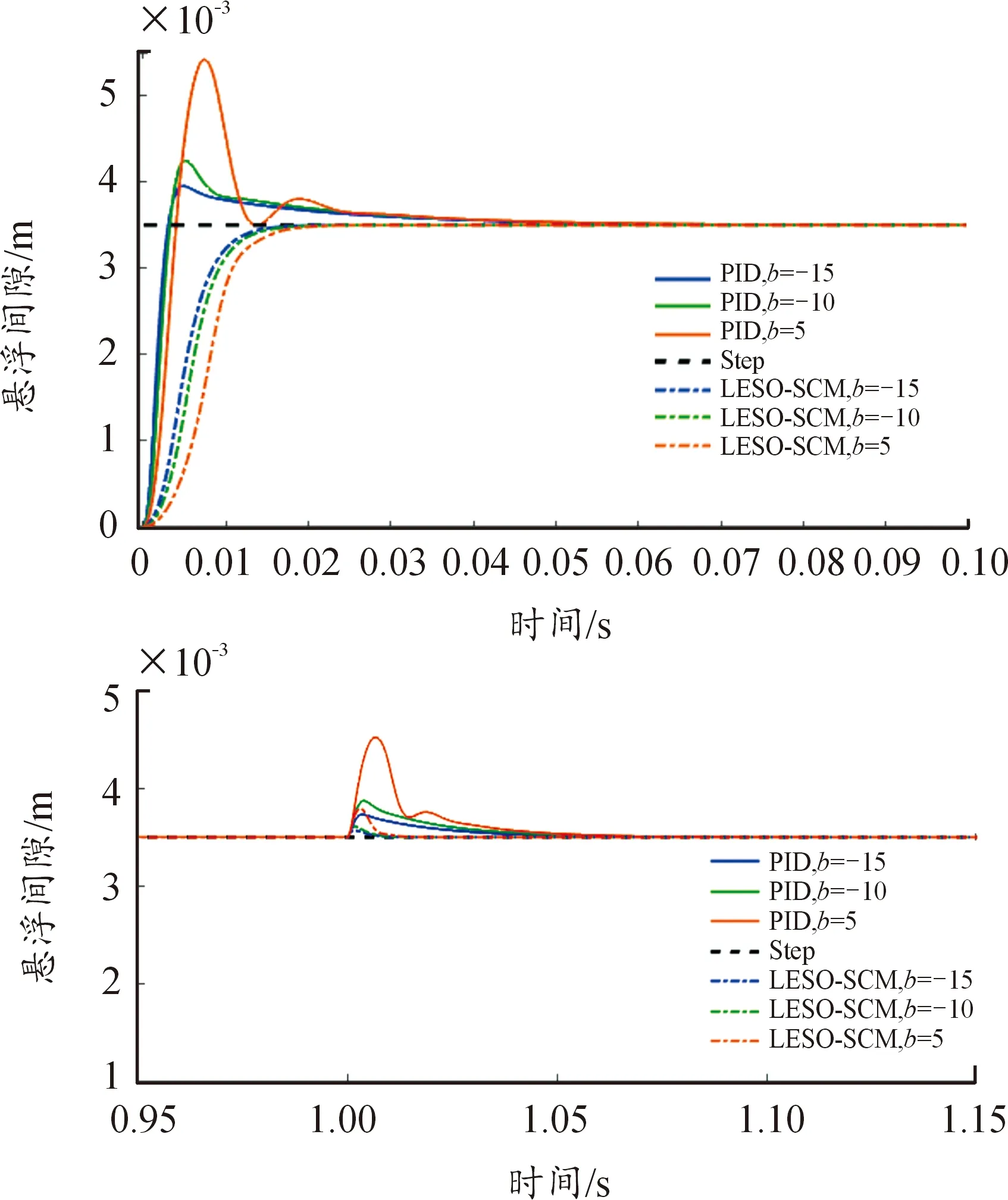
图10 鲁棒性响应曲线Fig.10 Robust response curve
4 结论
本文中围绕磁悬浮系统控制性能提升问题,针对系统具有的非线性、时滞性、强耦合特性,采用基于LESO的改进滑模控制方法,通过仿真结果研究分析得出以下结论:
1) 一般滑模变结构控制在系统的响应速度、超调量方面都优于PID控制,但是其中抗干扰性能较弱。
2) 基于LESO的改进滑模控制大幅度削弱一般滑模变结构控制系统抖振,相比于PID控制,响应时间减小到25%;在相同扰动条件下,基于LESO的改进滑模控制偏离平衡位置的最大距离是PID控制的20%,恢复时间是约为15%,进一步提高系统抗干扰性能,且能够更好的适应悬浮间隙的波动。
