基于数据映射优化的航空机匣变形测量偏差比对

刘 辉， 梁 晋， 叶美图， 郭建英， 李磊刚

（1. 西安交通大学 机械工程学院 机械制造系统工程国家重点实验室，陕西 西安 710049；2. 新拓三维技术（深圳）有限公司 创新实验室，广东 深圳 518060；3. 中国航发四川燃气涡轮研究院 强度传动试验研究室，四川 绵阳 621000）

1 引言

中介机匣是航空发动机上的重要承力结构［1］，其承载众多，结构复杂，所处位置特殊。因此，对机匣的安全性能的试验及评估已成为航空发动机结构设计和优化中不可或缺的一环。在过去的几十年里，有限元仿真为中介机匣的静力变形分析提供了极大帮助，得到了广泛应用。同时，除传统的千分表、应变片等手段外，光学非接触测量方法的数字图像相关（Digital Image Correlation， DIC）技术也能够获得机匣试验过程中的实时变形信息［2-3］。然而，在DIC 测量中，受诸如非均匀环境光、被测物自振等随机因素干扰，实测结果往往难以与仿真保持一致。因此，研究一种DIC测量变形与有限元模拟变形相互比对、相互验证的系统性方法，对于中介机匣的可靠性评估和结构优化设计具有十分重要的意义［4］。

目前，已有大量学者使用数字图像相关法实现有限元仿真模型的建立和比对验证。Gardner［5］等人为验证NASA 建立的火箭壳体屈曲设计因子和高保真度模拟方案的正确性，使用数字图像相关法获取大型金属复合材料圆柱壳体的强度测试数据，以验证仿真模型的正确性。加州大学Mohammad［6］等人为构建肺部的生物力学数值模型，使用DIC 系统测量猪肺稳定膨胀周期的表面变形数据，从而校准有限元模型的仿真参数。美国陆军航空与导弹中心的Owens［7］等人为了提取一种橡胶增韧环氧基胶材料混合断裂模型的J 积分和应力强度因子，将DIC 测得的位移数据映射到有限元模型中，以测得更加可靠的裂纹参数。阿尔伯塔大学Li［8］等人为建立能够指导双金属晶格结构设计的有限元模型，使用DIC 方法对316L 不锈钢双金属复合材料的拉伸和压缩变形进行测量，从而验证了数值模型的正确性。然而，模拟数据和DIC 数据之间存在着一些固有差异，在进行有意义的定量比对之前，必须校正这些数据差异，例如数据坐标系，网格类型和节点位置，测量的空间分辨率、数据滤波方法和应变计算类型等，而上述的所有研究中均未系统地给出有效的数据处理方法。从数据结构的角度来看，对于有限元数据和DIC 数据之间的对比验证，一种方法是使用一组基函数分解有限元数据和实验数据，对比分解基函数序列的振幅［9-12］，其优点是对比计算的数据量小，缺点是难以保证所分解的基函数能够完全代表实验或仿真数据。MatchID NV 公司的Pascal［13］等人提出一种借助有限元仿真数据生成试件表面的虚拟变形散斑图像进行数据对比的方法，虽然该方法能够自然地消除DIC 网格和有限元网格在应力计算、空间分辨率和滤波效果等方面的不一致，但通过贴图的方式生成虚拟图像不仅会消耗大量的计算资源，而且贴图本身存在着难以完全和DIC 网格对齐的缺陷，使得偏差比对结果的可靠性降低。因此，目前还需进一步研究更加鲁棒且操作简便的用于有限元验证的数据处理方法。

本文为了精确量化航空发动机机匣刚度试验中利用双目DIC 测量全场变形的整体偏差，提出了一种系统、全面的DIC 测量数据与有限元（Finite Element Method， FEM）仿真数据之间的映射方法。以有限元仿真结果为准，并以机匣肋板处的变形为例，首先使用FPFH 特征和迭代最近点法（Iterative Closets Points， ICP）解算出两类点云数据之间的相对位姿，进而完成数据的坐标对齐；然后使用遗传算法优化神经网络，完成了仿真网格数据向DIC 网格数据的高精度映射，从而消除了网格空隙带来的比对误差；最后，使用逐点最小二乘应变估计算法统一了有限元模拟和DIC 测量的应变计算模式，得到与DIC 属性一致的有限元比对数据，最终实现肋板处全场变形的测量偏差比对。

2 机匣变形测量偏差比对原理

本文所提出的偏差比对原理的目标是消除有限元（FEM）仿真数据和DIC 测量数据之间的固有不一致，如二者在世界坐标系位置，网格类型和节点位置，测量的空间分辨率、数据滤波方法和应变计算类型上的差异，从而利用有限元仿真数据和真实测量数据完成有意义的偏差对比验证，实现有限元仿真与DIC 测量结果的相互印证与闭环分析。

2.1 数据映射优化

为了消除有限元仿真数据和测量数据之间的不一致问题，首先要完成两组数据的映射优化，实现有限元数据向DIC 测量数据的映射。使用FPFH 特征和ICP 算法进行FEM 点云和DIC点云的位姿解算，从而实现两类数据的坐标统一，然后使用遗传算法优化的拟合神经网络，完成FEM 网格数据向DIC 网格数据的映射，具体流程如图1 所示。

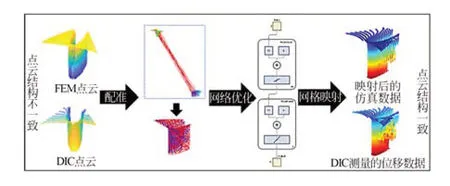
图1 数据映射优化原理Fig. 1 Principles of data mapping optimization

2.1.1 基于点云配准的全局坐标统一

在进行坐标统一的过程中，全站仪、激光跟踪仪等传统测量设备难以满足机匣变形的测量要求。首先，测量对象在加载过程中会产生形变，其形状并不固定，难以在被测物上布置跟随机匣变形的标记，也难以在有限元模型上找到其精确的对应点。其次，全站仪、激光跟踪仪等很难在现场进行在线校正，且由于不能进行离线计算，其单次测量时间受激光三角测距的计算时间影响，远远高于摄影测量所需时间，往往难以满足机匣动态刚度测试所要求的时间分辨率限制。此外，通过这种方式测量出的位置数据难以和DIC 测头的测量数据保持同步，造成对齐精度不可控，误差来源不可溯等问题。而采用点云配准的方式进行坐标对齐，不仅不用额外架设其他测量设备，避免了复杂的现场布置和设备校正等操作，同时，点云配准数据和变形数据是天然对应的，误差大小和来源是可溯源的。综合上述原因，本文采用点云配准方法进行数据坐标的全局统一，算法步骤如下：

（1）基于FPFH 特征粗配准。

FPFH 算子具有高效稳定的特征表达性能，在具有显著姿态差异的配准任务中具有较强的优势。根据FPFH 特征查找到的特征点可用于FEM 点云和DIC 点云相对位姿初值的计算，计算公式如式（1）所示：

其中：XFEM是FEM 点云上的特征点，XDIC是DIC点云上对应于FEM 点云的特征点，T1是从DIC点云变换到FEM 点云的刚性变换初值，实现点云粗配准。

（2）基于ICP 算法的精配准。

为保证两组点云相对位姿的求解精度，还需使用ICP 算法对初始变换后的两组点云进行迭代优化［14-15］，本文采用迭代最近点法（Iterative Closets Points，ICP）令待配准的DIC 点云为集合P={pi}，i=1，2，3，…，n，基准FEM 点云集合为X={xi}，i=1，2，3，…，m。为了确立两个点云之间的对应点，构建点云KD 树查找所有空间最近点，以此计算点集P到点集X之间的位姿变换关系，迭代的优化方程如式（2）所示：

其中：ni是xi点所在局部平面的法向量，R为点集P到X之间的旋转矩阵，T为点集P到点集X的平移向量。

2.1.2 FEM 与DIC 的网格映射原理

一般情况下，待比对的FEM 网格和DIC 网格类型和节点位置都不相同，为了完成偏差比对必须首先完成网格映射。DIC 数据节点的三维坐标是通过双目测头重建的机匣肋板表面点云，其数据类型是一个曲面，而有限元仿真的模型点云是一个三维实体，其中不仅包含表面位移数据，同时也包含体内位移数据。在实际转换的过程中，FEM 空间点云中的表面点云和内部点云难以区分，若采用直接插值的方法，FEM 表面节点将会受到内部节点位移量的影响，从而与DIC算法模型特征产生新的不一致，在比对的过程中引入额外偏差。此外，不同的插值类型对不同表面形状的插值结果差异较大，难以找到针对所有表面形状的最佳插值方法。而BP 神经网络通过机器学习的方式进行空间位移场的拟合，可以根据训练集数据调整出最佳的模型参数。因此，在这种情况下，相比于插值方法，使用神经网络对有限元仿真模型（理论真值）的空间位移场进行拟合是一种更加通用、方便的数据映射策略。

综上所述，为避免引入额外偏差，本文采用遗传算法优化神经网络［16-18］拟合FEM 的空间位移场，根据配准后的DIC 节点坐标，将有限元网格映射至DIC 网格上。算法的具体流程如图2 所示。用于FEM 向DIC 的数据映射优化建模步骤如下：

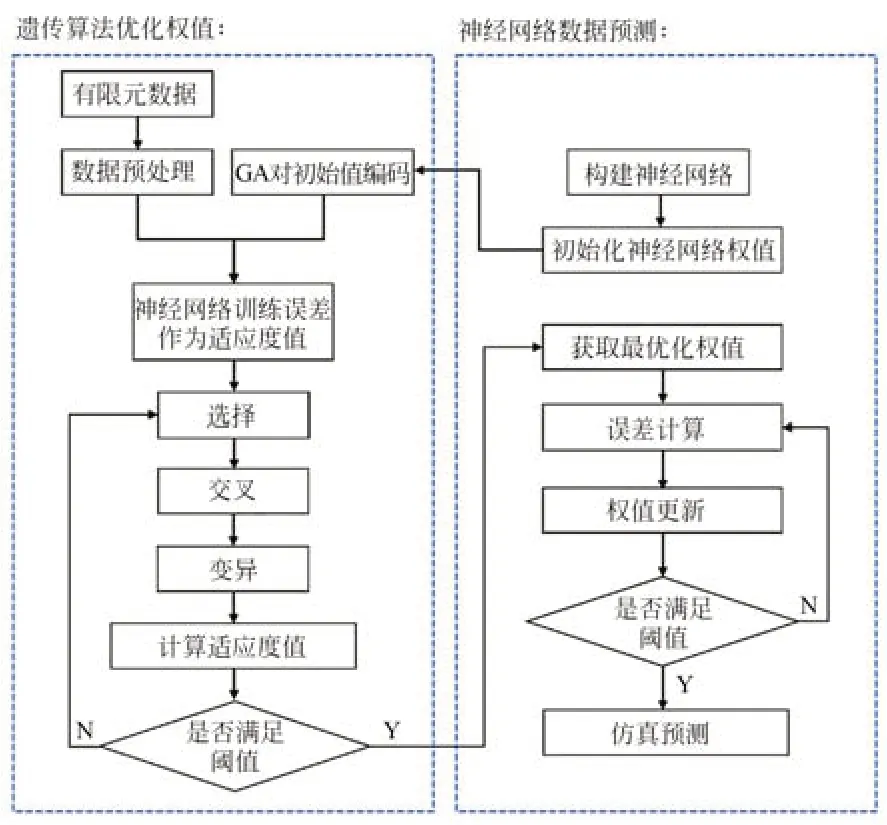
图2 遗传算法优化神经网络Fig.2 Neural network optimized by genetic algorithm

（1）构建BP 神经网络参数。

出于对计算效率的考虑，本文采用结构为3-25-3 的神经网络进行拟合，即输入层有3 个节点，隐藏层由25 个节点组成，输出层有3 个节点。激活函数使用Sigmoid 激活函数。神经网络结构如图3 所示。

（2）遗传算法优化神经网络权值和阈值。

通过对神经网络中的所有权值进行编码，获得单个权值序列［s1，s2，s3，…，sL］和阈值序列［γ1，γ2，γ3，…，γL］。将所有阈值和权重按顺序拼接形成一个染色体。染色体的长度计算公式如式（3）所示：

其中：ni为输入层节点数，n为隐藏层节点数，n0为输出层节点数。在本文中，输入层有3 个节点，隐藏层有25 个节点，输出层有3 个节点，因此每条染色体的长度为3×25+25+25×3+3=178。

遗传方法包括选择、交叉和变异。选择操作一般使用轮盘赌等方法产生新种群。交叉操作产生最佳性状的重要手段，如果令两条染色体XiA和XiB相互交叉，那么新个体如式（4）所示：

其中：α＜Pc且0 ＜α＜1，Pc为父母染色体发生交叉的概率。

此外，本文使用均匀突变操作，将突变概率设置为Pm，设置突变点xk的范围为［Ukmin，Ukmax］，突变点的新遗传值如式（5）所示。

其中，r是［0，1］范围内的随机数。

（3）训练BP 神经网络。

通过将网络权值和阈值导入遗传算法中进行优化，得到新的权值和参数，将其分配给BP 神经网络。然后根据BP 算法，输入训练集进行学习和训练，直到预测误差满足期望值。

有限元数据作为一种数值模型，其数据相对与DIC 数据具有以下两点优势：①数据分辨率：有限元仿真是一个理论模型，其计算的分辨率原则上可以取到无穷小，而立体DIC 的测量数据分辨率受到镜头分辨率，像元尺寸，测量幅面大小等因素的制约，存在一个最小极限。根据精度比对的惯例做法，一般倾向于将分辨率（精度位数）更高的数据作为基准。②环境噪声：有限元模型是理论模型，其计算数据不包含噪声，以此拟合出的空间位移场能够完全对应于原始数据，将其作为比对基准是可靠的。而DIC 测量数据包含了环境噪声，如果用DIC 数据作为训练集拟合其空间位移场，噪声部分会对拟合结果造成较大影响，以此作为比对基准是不可靠的。此外，DIC数据作为待验证数据，理应维持其原始测量值，得到更直观的偏差计算结果。

由于以上原因，本文将有限元节点坐标及其对应的位移值作为训练集，拟合得到空间内与FEM 数据关联的连续位移场，然后将DIC 节点坐标作为输入进行预测，输出节点位移量，从而完成从有限元网格向DIC 网格的映射。

2.2 空间变形计算原理

数字图像相关法（DIC）直接测量得到的位移数据往往含有一定噪声，而由FEM 得到的数据不包含噪声，这导致了二者在应变计算方法上的差异，为了消除这种差异，本文统一对两组位移数据使用空间逐点最小二乘应变估计算法［19］，计算Green-Lagrange 应变张量，以此保证偏差比对的同一性和有效性，Green-Lagrange 应变张量计算公式如式（6）所示：

其中：(u，v，w)为当前点的位移，(X，Y，Z)为当前点的三维坐标，εxx，εyy，εzz，γxy，γxz，γyz为当前点在空间内的格林应变张量。

式（6）中的位移梯度对噪声敏感，为了消除噪声，本文扩展了Pan［19］等人提出的应变窗思想，将三维位移数据进行平面投影滤波，即使用位移数据(u，v，w)组成的最小二乘拟合的超平面参数求解位移梯度数据，超平面方程如式（7）所示：

其中：(x0，y0，z0) 是当前应变窗的中心点，(x，y，z)为当前点的空间坐标，(up，vp，wp)为当前点的空间位移。

本文在目标点云区域划分空间球体区域作为计算应变的应变窗，将点云数据带入式（7），即可求解出该应变窗在空间内3 个方向上位移拟合超平面，通过超平面参数确定滤波后的位移梯度，用于式（6）中的格林应变张量的计算。根据计算出的Green-Lagrange 应变张量，进而计算出当前空间点的3 个主应变。当前空间点的主应变ε1，ε2，ε3即为方程（8）的解：

其中，J1，J2，J3为应变张量不变量，计算公式如式（9）所示：

3 测量试验与结果

中介机匣结构特殊，内外环呈规则圆形，环壁厚低于0.5 cm，且二者之间由数个周向均布的对称弧形肋板连接。肋板本体在机匣内外壁的连接处截面和厚度均最小，因此在机匣性能试验中，匣体的整个肋板及与内外壁的连接部位属于最薄弱处，极易引起应力集中，是试验任务的主要关注点。精确量化其承载后的变形信息对结构安全性能评估和优化设计具有重要意义。因此，本文以顶部肋板处的DIC 和FEM 数据进行验证和分析。

3.1 视觉变形测量及有限元仿真

3.1.1 试验系统搭建

本文使用新拓三维（XTOP）的立体DIC 系统（XTDIC®）测量航空发动机机匣顶部肋板的全场变形。测量系统由两套双目视觉测量单元组成，相机分辨率为2 448×2 048 pixel，像元尺寸为3.45 μm/pixel，配备镜头型号为RICOH，焦距为25.0 mm，相机之间的立体角为25.5°。两套双目DIC 设备分别拍摄肋板的左右两面，使用马克笔在待测的顶部肋板上点涂用于匹配的散斑特征，重建出的肋板点云拼接通过两套双目相机的全局统一标定实现，具体的实验场景及制作的散斑特征如图4 所示。

图4 机匣实验场景Fig.4 Testing site of casing

机匣的主要的承载部位是呈180°分布的两个肋板。肋板本体呈对称圆弧形，在内外壁的连接处截面最小、壁最薄，中间部位截面和壁厚略微增大，是本次试验任务的关注重点。本文使用结构静力与疲劳试验器对机匣进行加载，加载装置和加载方式如图5 所示，最大加载载荷为-40 kN，加载过程如图6 所示。

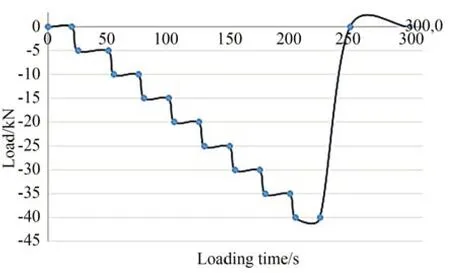
图6 加载曲线Fig.6 Loading curve

3.1.2 视觉测量结果及有限元仿真结果

两套DIC 设备测量的顶部肋板位移场和应变场如图7 所示。从图中可以看出，虽然两侧位移场分布基本一致，但肋板右侧位移数据分布不均匀，存在一定的测量偏差。

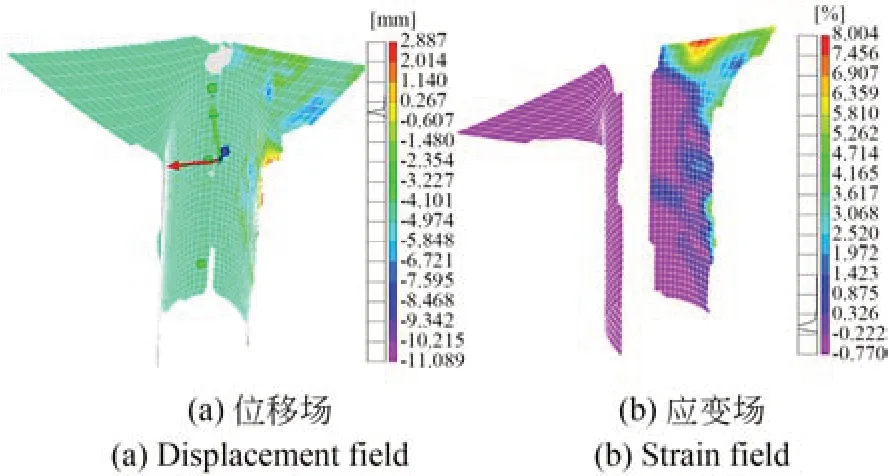
图7 DIC 测量结果Fig.7 DIC measurement results

使用有限元方法，在相同的边界条件下对机匣模型进行静力学仿真分析。模型材料选择钛合金，材料密度为4 620 kg/m3，杨氏模量为9.6×1010Pa。使用四面体网格划分CAD 模型，如图8（a）所示。对机匣外圈整体施加支撑约束。载荷以线积分的形式施加在机匣内圈的下半圈，如图8（b）所示，载荷大小随θ按照余弦变化，载荷施加条件满足式（10）的约束。

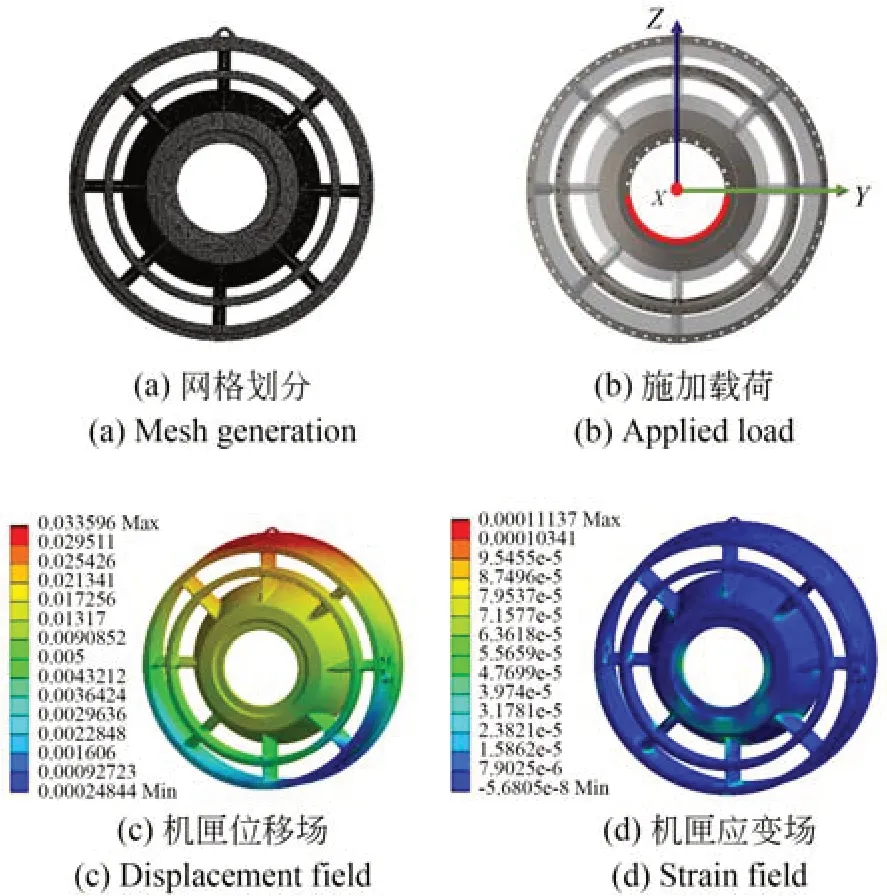
图8 有限元仿真结果Fig.8 FEM simulation results

其中：fz(θ)为竖直方向的分力，F为当前时刻加载装置施加的压力，a为余弦分力的幅值，可根据约束条件求出。

最终得到如图8（b）和图8（c）所示的仿真结果。从图中可以看出，仿真得到的最大位移量为0.033 596 mm，最大主应变为111.37με。

3.2 机匣测量偏差比对

3.2.1 数据坐标统一与映射优化

由于DIC 重建出的肋板数据和FEM 仿真得到的肋板数据是在不同坐标系下描述的，直接对比各自x，y，z三个方向的变形分量没有意义，因此需要将DIC 数据和FEM 数据统一到一个全局坐标系中描述。采用2.1 节中所述的方法完成两组点云的坐标统一。

分别计算空间中两幅点云的FPFH 特征，搜索得到两组点云对应的特征点，从而进行点云相对位姿初值的计算，如图9 所示，然后使用ICP 算法进一步对位姿初值进行迭代优化。

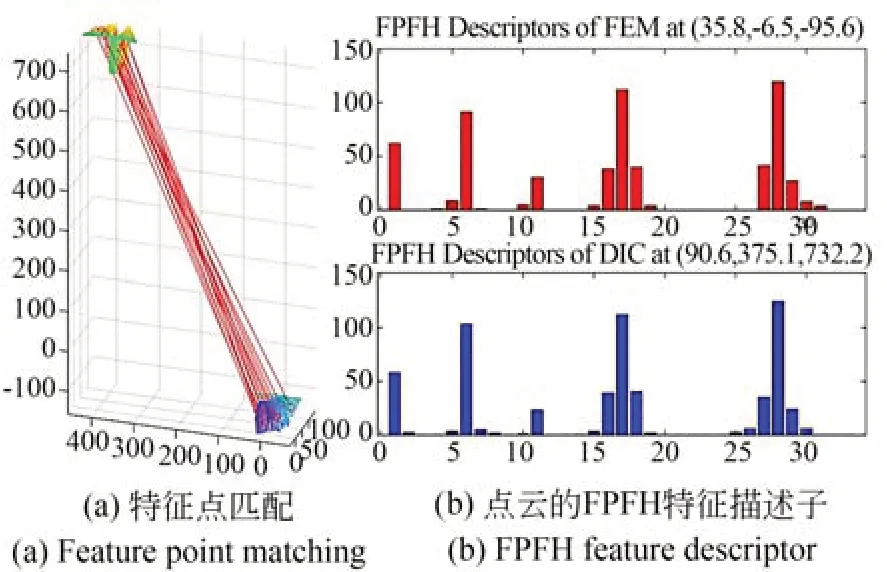
图9 FPFH 特征匹配Fig.9 FPFH feature matching

由特征点计算出粗配准变换矩阵，粗配准后使用ICP 算法对配准位姿进行迭代优化，精配准后两组点云之间点距的均方误差为0.101 5 mm，配准效果良好。粗配准和精配准的效果如图10所示。

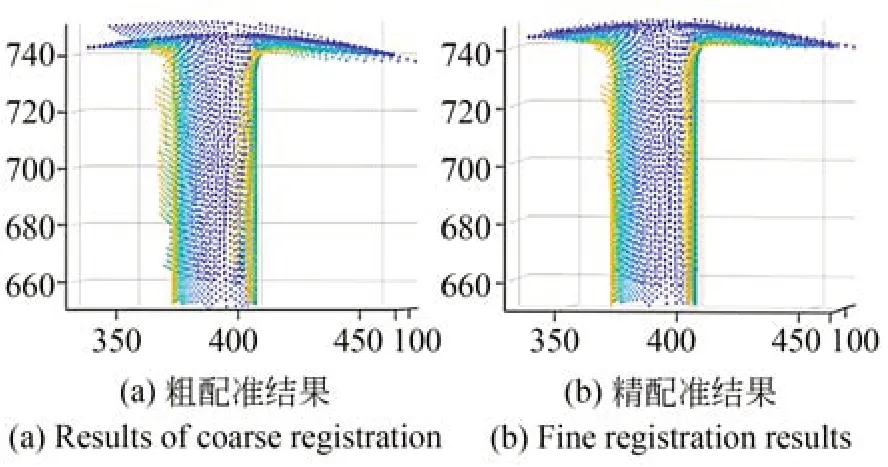
图10 点云配准效果Fig.10 Point cloud registration results

3.2.2 数据映射及精度验证

由于DIC 网格和有限元网格在划分时即存在固有不一致，因此在比对前还需进行DIC 网格和FEM 网格的映射和转换。

本文使用遗传算法优化神经网络实现不同网格之间的转化。将有限元模型的仿真数据作为训练集，输入网络进行训练后，再将DIC 网格节点输入网络，得到FEM 在DIC 节点处对应的仿真数据，从而预测FEM 网格向DIC 网格的转换。验证集的预测效果如图11 所示。从图12 中可以看出，拟合神经网络的预测效果良好，在验证集上的输出的误差小于1×10-6mm。

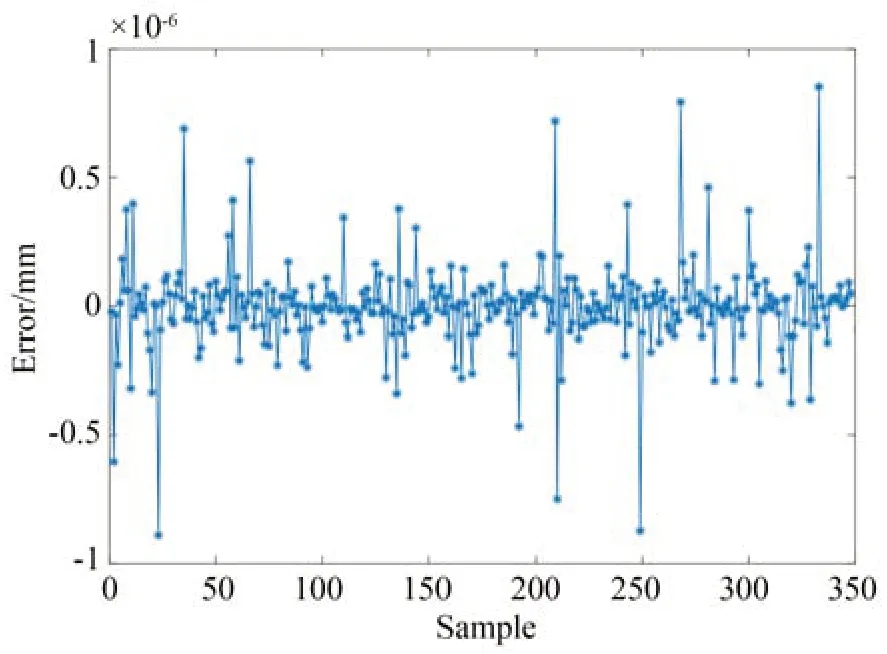
图12 神经网络的预测误差Fig.12 Prediction error of neural network

此外，同时使用自然邻域插值方法、最近邻插值和线性插值方法［20］进行网格映射，以对比本方法的映射精度和映射效率。有限元网格为空间四面体网格，DIC 网格为平面四边形网格，如图13 所示。每一个DIC 网格节点位移的理论真值通过其所在四面体网格节点插值得到。

图13 DIC 网格和有限元网格示意图Fig.13 Schematic diagram of DIC grid and finite element grid

在FEM 点云中随机选取12 组点云作为验证集，同时验证神经网络预测结果和插值结果的计算精度，表1 列出了12 组验证集上不同方法的效果。从表1 中可以看出BP 神经网络的数据映射误差最小，自然邻域插值方法的误差小于其他插值方法。从标准差上来看，BP 神经网络数据略小于自然邻域插值。

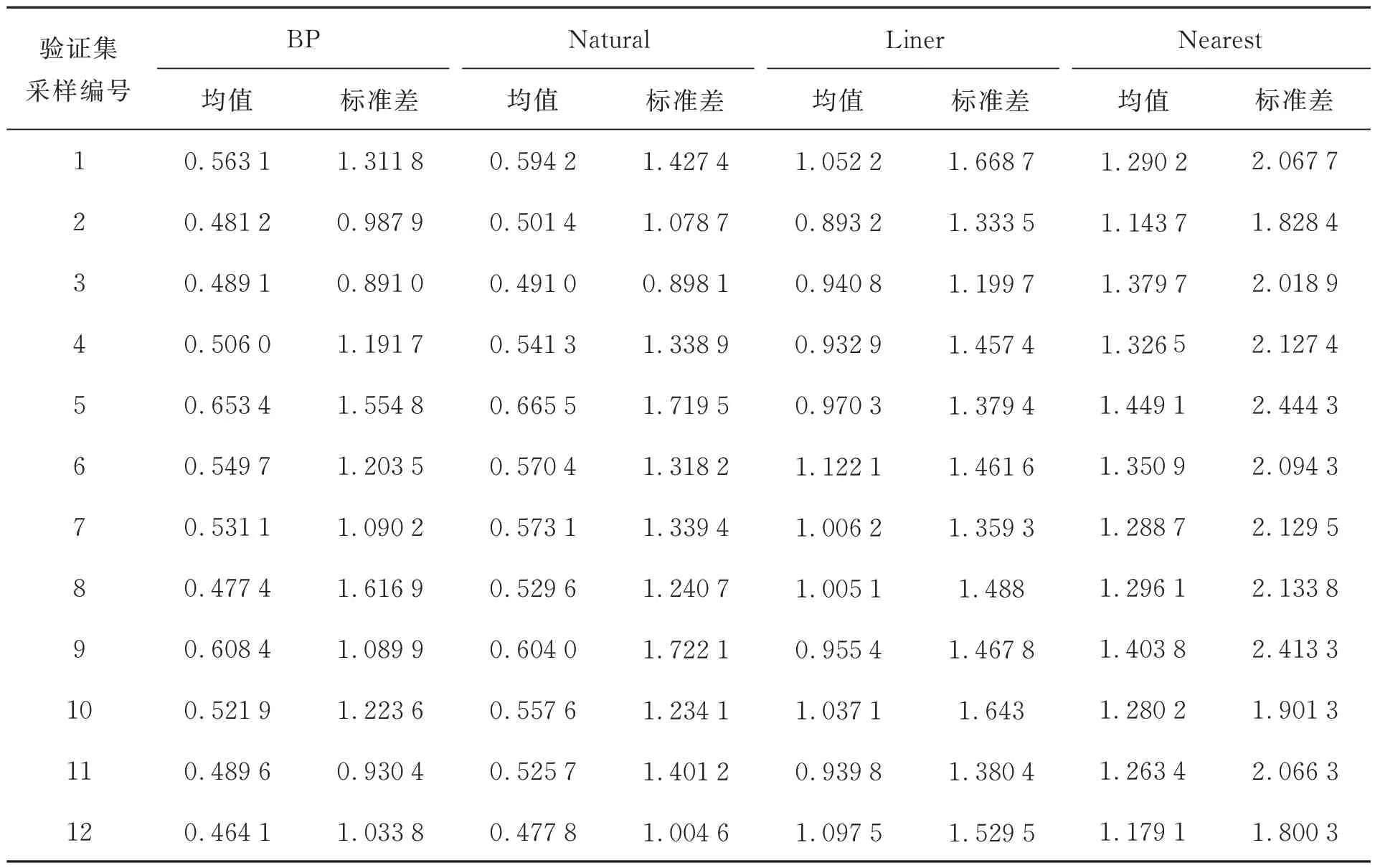
表1 不同方法的数据映射误差Tab.1 Data mapping error for different methods（10-6 mm）

图14 显示了本文方法和自然邻域插值方法在验证集上的百分比误差，从图中可以看出，本文方法误差不超过2%，而表现最优的插值方法的误差最大超过了3%，证明了本文方法在精度上优于其他插值方法。

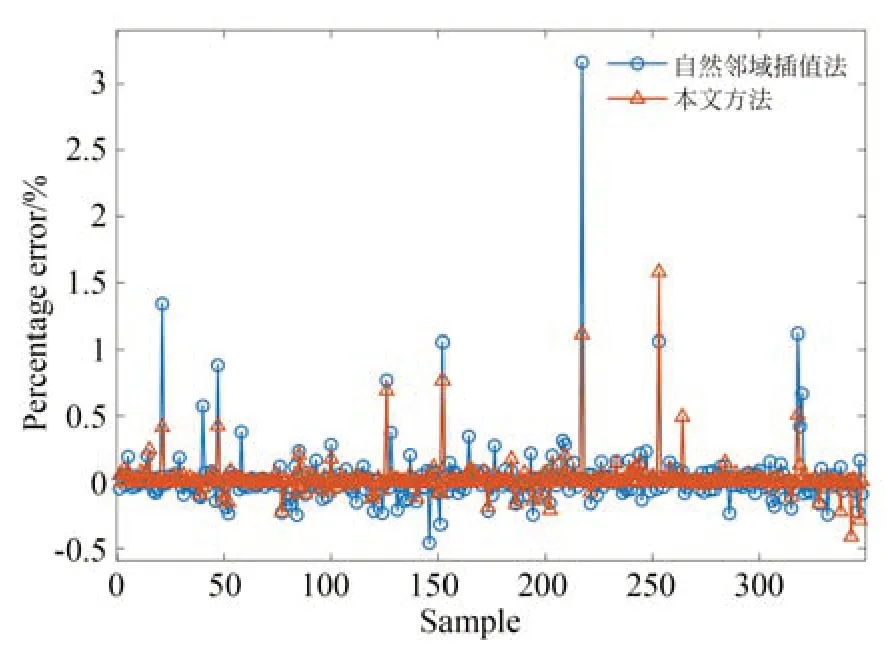
图14 网格映射的百分比误差Fig.14 Percentage error in grid mapping

在时间效率上，分别对本文方法、自然邻域插值法、最近邻插值法和三线性插值进行分析，在验证集上（350 个点）程序运算时间统计如表2所示。从表2 中可以看出，本文方法的计算时间远远少于其他插值方法，计算效率较高，更加适用于对大型数据进行处理。

表2 计算时间效率分析Tab.2 Computational time efficiency analysis （s）

映射前后的有限元位移场如图15 所示。映射后的FEM 数据与DIC 数据在空间坐标位置完全对应，有效消除了FEM 和DIC 数据之间的世界坐标系位置，网格类型和节点位置和测量的空间分辨率的不一致。

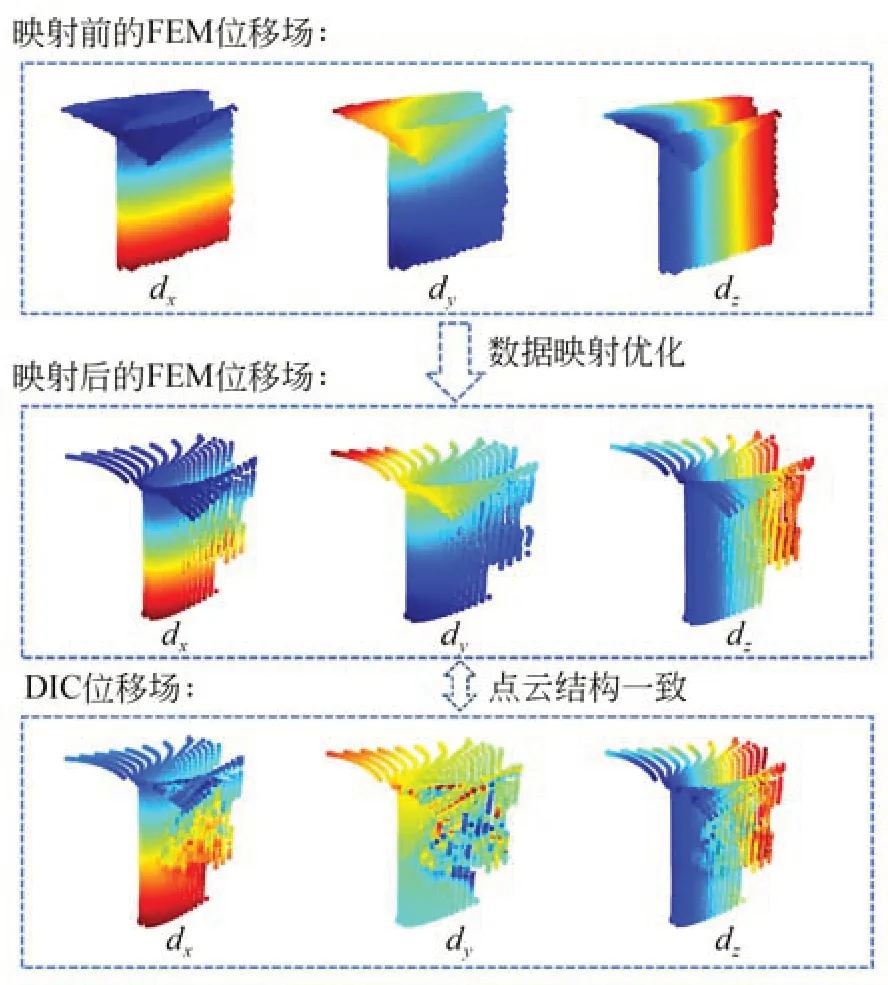
图15 数据映射优化结果Fig.15 Data mapping optimization results

3.2.3 空间变形计算与偏差对比

本文使用空间包围球作为点云数据的应变窗，使用逐点最小二乘应变估计算法计算DIC 位移数据的应变量。同时，为保证数据的统一性，对FEM 位移数据进行同步处理，最后实现有限元仿真数据和DIC 测量数据的闭环分析和相互印证。

本文对比FEM 和DIC 数据的3 个主应变ε1，ε2，ε3，变形偏差场的比对结果如表3 所示。使用DIC 测量的应变数据在肋板右侧面和右上方存在较大的偏差，说明了在视觉测量过程中，测量肋板右侧面的双目立体DIC 设备存在较大的环境噪声干扰。经过对实验现场环境分析，得出噪声来源如下：①实验所使用的双目DIC 设备采用工业灰度相机，对蓝光更为敏感，所以每台DIC 都配备了蓝光光源照射被测表面，而肋板右侧面正对窗户，相对于左侧受到了更大程度的环境光干扰，因此偏差较大。②机匣加载方式为阶梯式加载，在每次启动加载和保持载荷的瞬间存在一定震荡，引入了一定的测量误差。

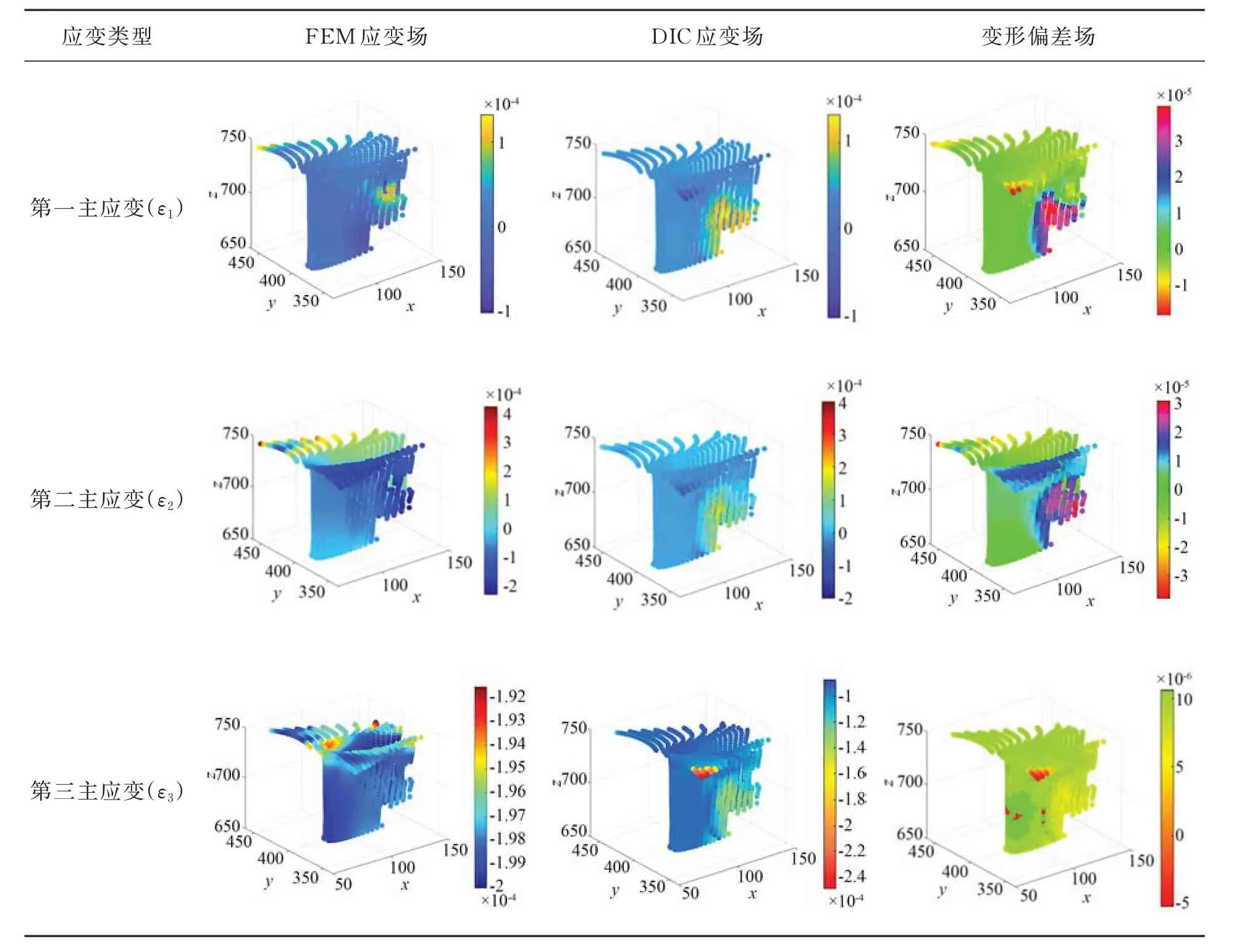
表3 全场变形偏差比对结果Tab.3 Full-field deformation deviation comparison

将DIC 测量的第一主应变和FEM 仿真的第一主应变进行定量的偏差比对结果如图16 和图17 所示。从图16 中可以看出，本次机匣变形的视觉测量结果和有限元仿真表现出较强的一致性，证明了有限元模型的正确性，同时也证明了该实验中DIC 方法测量的机匣变形数据的准确性。从图17 中可以看出，以有限元仿真结果为基准，在本次实验中，DIC 应变测量系统的测量偏差小于50 με。

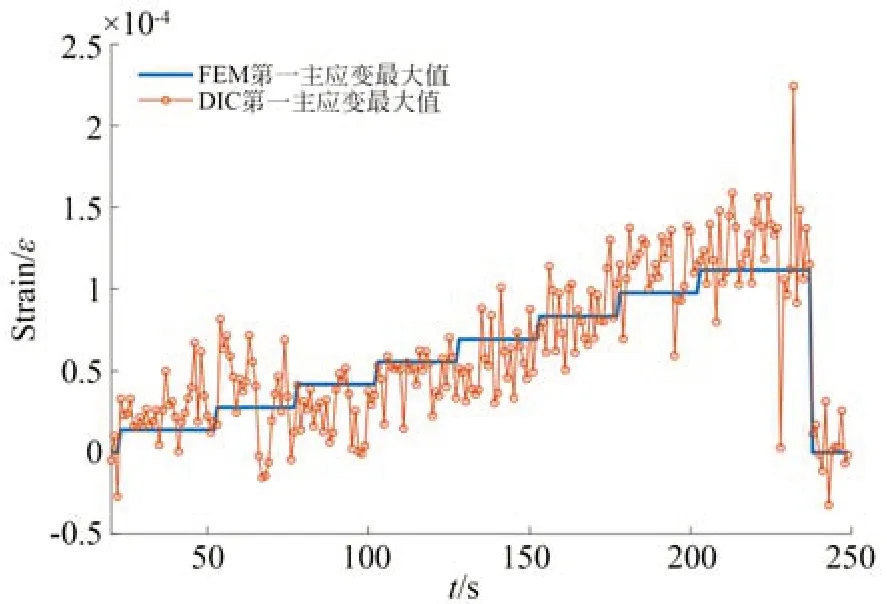
图16 FEM 和DIC 的第一主应变最大值Fig.16 maximum principal strain of FEM and DIC

图17 应变比对偏差Fig.17 Deviation of strain comparison

此外，从整体算法流程和数据结果上看，本文提出的方法相对于其他方法，诸如基函数分解方法和散斑贴图方法具有其特有的优势。基函数分解方法是指使用一组基函数分解有限元数据和实验数据，对比分解基函数序列的振幅，其优点是对比计算量小，但计算结果无法反映偏差的具体位置，而本文方法可以直观地显示DIC 测量偏差存在的具体位置。相比于散斑贴图的方法，本文方法操作简单。散斑贴图是人为主观对齐DIC 计算的感兴趣区域，难以保证和度量对齐精度，而本文采用ICP 算法进行对齐，误差来源可溯可控，节点映射精度更高。

4 结 论

本文提出了一种系统、全面的DIC 测量数据与有限元仿真数据之间的映射方法。可有效的消除DIC 数据和有限元数据在世界坐标系位置，网格类型和节点位置，测量的空间分辨率、数据滤波方法和应变计算类型上的固有差异，实现了有限元仿真和DIC 全场测量的偏差比对。采用“虚实结合”的方式，构建了有限元仿真和DIC 光学测量的闭环分析方法，使二者之间能够相互印证。

从航空机匣肋板测量偏差比对试验中可以看出，本文所提方法的网格节点的映射精度优于1×10-6mm，映射百分比误差小于2%，优于其他各类插值方法。此外，本文算法的数据映射速度较快，在进行数据量较大的比对任务时具有一定的时间效率优势。仿真变形和DIC 变形的偏差云图与偏差曲线具有良好的一致性，且能够显示DIC 测量偏差存在的具体位置。此外，本文所提方法具有较强的通用性，可以用于但不仅限于机匣肋板的偏差比对，在未来航空发动机机匣及类匣体的研制和测试领域中具有良好的应用前景。