多变量控制图及过程能力指数在生产中的应用

雷彬文 龚立雄

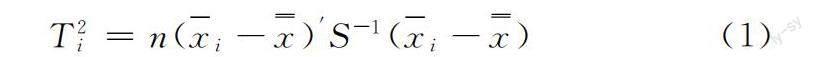
[摘 要]针对单一控制图对小波动工序过程不能准确识别和诊断的问题，提出将多变量T²和MEWMA控制图结合起来诊断生产过程的受控情况，再以多变量过程能力指数进一步判定制造企业的工序过程。以多变量T²、MEWMA控制图以及规范区域为长方形的修正过程能力指数算法等理论为基础，以某电子企业主板控制器生产过程为对象，对影响焊接过程质量的特性因素进行分析。基于联合多变量T²、MEWMA控制图及过程能力指数，来诊断生产过程的工序状态及影响因素，对样本数据进行了分析和计算。结果表明：所采用的多变量质量诊断算法误差较小，能有效监督和控制生产过程。

[关键词]多变量控制图；过程能力指数；生产过程控制；质量诊断

[中图分类号]TQ460.6[文献标识码]A

控制图和过程能力指数是质量控制的重要手段，对于降低废品率、提升产品质量和管理水平具有重要作用，已被应用到机械、电子、汽车、化工等多个行业，成为制造企业在线质量诊断和控制方法的技术支撑^[1]。目前，众多学者对控制图和过程能力指数的研究以单变量和多变量控制图和过程能力指数为主，以Shewhart控制图为基础，关注过程控制的变异。常用的包括χ²控制图、T²控制图、W控制图。Nijhuis等提出了同时监控多变量过程分布特征和过程能力的TC2控制图^[2]。Wu等对过程能力指数度量问题及应用进行了综述，并进行了比较研究，指出多个相关性过程能力指数的计算和度量是一个值得研究的问题^[3]。Pearn等提出了一种估计Taan等所提出的多元过程能力指数方法，并给出了MPCI置信区间^{[4- 5]}。Ahmad等基于不合格品率准则及协方差距离，提出了一种新的多元过程能力指数，该能力指数能评价正态和非正态过程^[6]。罗碧青等在粉末直接压片工艺中借助过程能力指数，获得较高性价比的压片工艺配方^[7]。郭佳晟通过蒙特卡洛（Monte Carlo）模拟法分析了WAB控制图在过程失控时的性能表现，并与T²控制图进行比较^[8]。此外，部分学者提出了基于神经网络理论的智能多元质量诊断算法^[9-10]。但该算法需要大量经验和统计数据对所构建的神经网络模型进行训练，对小样本数据不太适用。T²控制图在解决质量控制和质量诊断为题的重要方法，但多变量质量特性间存在相关性，并且多变量单值T²控制图对小波动敏感性不强，影响质量诊断的准确性。本文在T²控制图的基础上，引入过程能力指数和多元指数加权移动平均（Multivariate Exponentially Weighted Moving Average，MEWMA）控制图联合诊断制造企业的生产状态，并以某制造企业为案例进行了分析，分别采用T²、MEWMA控制图以及修正区域为长方形的算法计算多变量过程能力指数，剔除原始数据中不合理的数据，运用Xbar-R控制图进一步分析原因，将算法结论与企业生产实际进行对比，表明本文所提出的T²、MEWMA控制图、过程能力指数联合质量诊断的方法可行，能广泛应用于制造企业生产过程的质量诊断和控制。

1 多变量控制图及过程能力指数

1.1 多变量T²控制图

统计量表达式：

使用T²控制图可以同时监视两个或多个相关变量的过程位置是否受控制。此控制图是 Xbar 控制图和单值控制图的多变量形式。

1.2 MEWMA控制图

多元指数加权移动平均（MEWMA）控制图是用来对多变量过程X分布中心微小偏移进行统计监控的控制图。MEWMA控制图表达式为：

式中，R为P维对角矩阵，对角矩阵元素为r_i（0i<1，i=1，2，…，p）。

1.3 多变量过程能力指数

要进行过程能力分析，首先必须确定关键质量特征值，然后判断其数值的特性，最后按照计量值型、计数值型相对应的过程能力分析方法步骤进行分析^[12]。

2 案例分析及应用

2.1 案例背景及影响质量因素

某电子企业主要生产品牌豆浆机主板控制器。近期，该主板控制器生产过程中出现了质量缺陷有所回升的不良趋势，因而需从5M1E综合分析，找出影响质量的具体原因。其主板控制器生产流程如图2所示。

工序中，点红胶、ICT测试（In Circuit Tester，自动在线测试仪）为关键工序，规定回流焊、波峰焊为特殊工序。該企业统计数据表明：造成该企业产品缺陷比例最高的是材料不良，这需要与供应商沟通，加强对供应商的管控；其次是拉丝短路，该缺陷占比30%左右，是质量控制的重点。拉丝短路不良现象的主要原因存在于波峰焊工序中，波峰焊工序的锡炉温度、助焊剂比例和波峰频率等都有可能是关键因素。影响波峰焊质量的重要因素有短路、焊锡球、虚焊、空洞、拉尖等。图3鱼骨图呈现了波峰焊缺陷的影响因素。

从文献[13-14]了解到，在焊接过程中影响焊点焊接质量的主要因素有：波峰高度、轨道倾角、传送速度、锡炉温度、预热温度以及助焊剂比重。因此，本文将以选定此豆浆机主板控制器波峰焊工序中点焊的助焊剂比例x₁、预热温度x₂、焊锡液面高度x₃、轨道倾角x₄和波峰宽度x₅这5个质量特性作为分析的对象。根据经验，后3个质量特性存在着自相关性，因此重点对其进行过程能力计算分析。

2.2 原始数据及控制图分析

本文研究的数据来源于案例企业某品牌豆浆机主板控制器的生产实际数据，经统计分析和整理而成。重点对具有自相关性的x₃、x₄、x₅数据进行质量控制图和质量特性计算，并与原文进行对比分析。x₃、x₄、x₅原始数据如表2所示。

可以看出用几何平均法计算出的多元过程能力指数为1.058>1，满足基本要求，但并不是每个质量特性均满足要求。而用差异系数算法求解的多元过程能力指数为0.9801<1，说明过程能力一般，不满足基本要求。因此，还需进一步对存在相关性的3个质量特性进行分析和判别。

2.3 进一步讨论

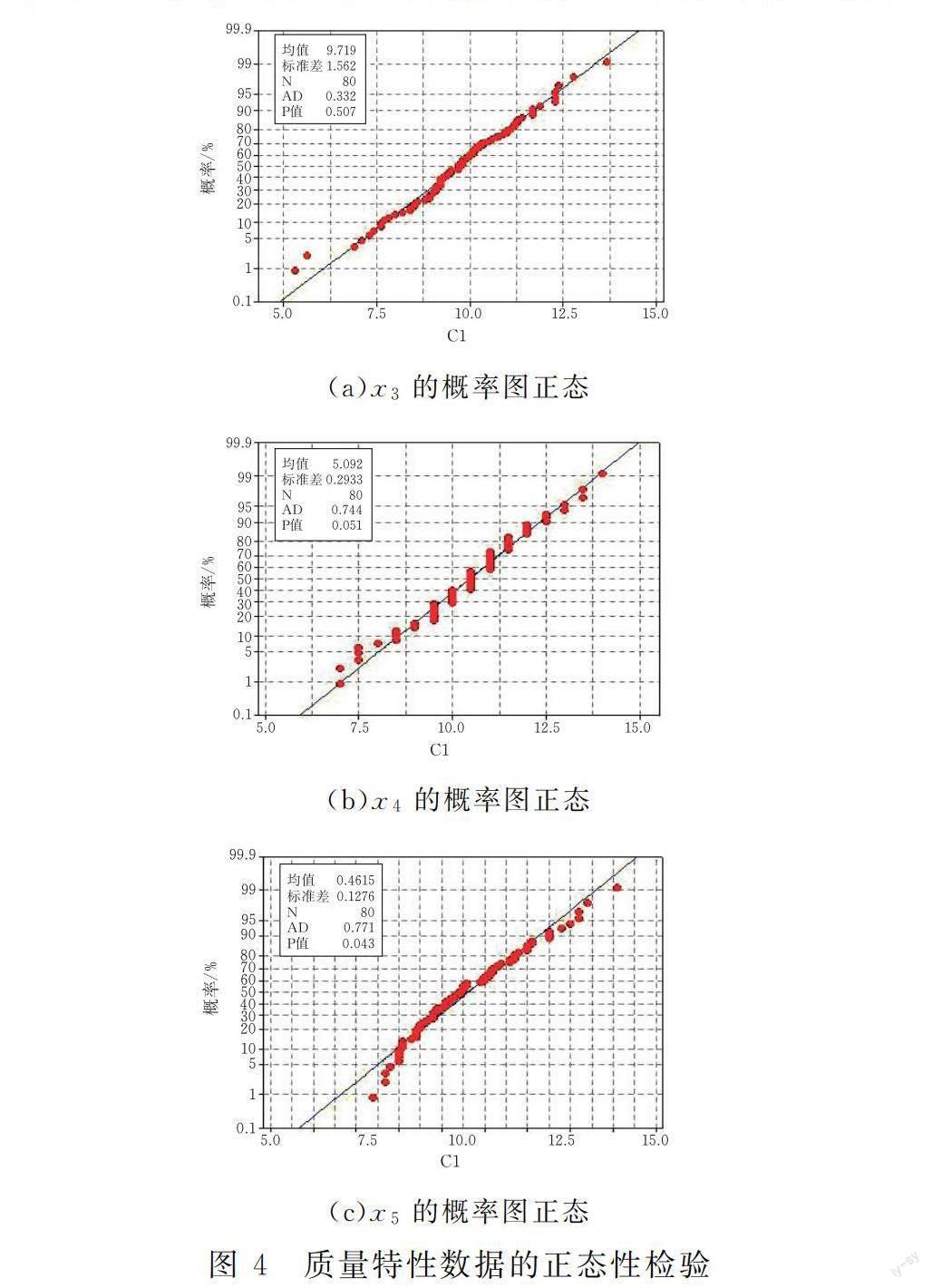
原始数据的样本子组容量为1。为更进一步研究多变量控制图，在80组原始数据基础上随机生成一组数据，使得样本子组容量为5。在后面的多变量控制图与过程能力指数研究中选取30组数据进行分析。x₃、x₄、x₅（即焊锡液面高度x₃、轨道倾角x₄、波峰宽度x₅）3个质量特性数据的正态性检验见图4，说明随机生成的部分数据对研究结论影响极小，可以作为小样本数据进行进一步分析和讨论。

步骤1. T²、MEWMA控制图及相关性变量的Xbar-R控制图

将新的数据分成30组，求解每组的平均值、样本方差、统计量T²，利用Minitab做T²控制图。30组数据中每组数据均值如表3所示。

设30个样本均值

因此，计算样本统计量T²如表4所示。

由该企业生产背景得α=0.05，又n=5，p=3，查F分布表得F_0.05（3，118）=2.68；此时上控制线UCL=3×29×4118×2.68=7.90，得到T²、MEWMA控制图（图5）。T²控制图中点13和点16出界，需要剔除重新计算。

图6可以看出：多容量样本数据为30组时，x₃均值-极差控制图都正常；x₄的均值-极差图第16个点超出3个标准差，均值图中后14个点落在中心线两侧的C区内（在实际生产过程控制中此时应增加抽样点来判断过程是否异常），极差图中有超过连续9点在中心线同侧，也是造成第一次使用T²控制图第16个点异常的原因；x₅均值图正常，极差图中有连续9点在中心线同侧。

步骤2. 剔除不合格数据，重新计算T²和MEWMA控制图以及Xbar-R控制图

剔除12、13、16组数据后，剩下的27组数据重新计算

样本协方差矩阵均值

计算控制上限为7.92。则T²、MEWMA、Xbar-R控制图。

图7中，27组多容量样本绘制的T²控制图所有打点值均在控制限范围内，此时过程基本处于受控状态。而自相关的x₃、x₄、x₅变量组的 MEWMA控制图也显示过程基本处于稳定，说明剔除不合格的数据后，该生产过程处于基本稳定状况，但是仍有时出现波动状态。

图8中，x₃均值-极差图过程稳定；x₄极差图中第11点超出3个标准差，考虑该点所代表的样本数据抽样取值时的合理性，或是记录数据有误，或是抽样时存在某个不合格样品；x₅极差图后12点有连续9点在同一侧。

T²控制图经过2次控制限调修生产过程处于基本稳定状态。从各样本数据的单值图中可知，经过剔除3组数据后，均值图处于基本受控状态，但极差图在后12组数据中有连续9点在中心线同侧，需要进一步分析原因。而数据中x₃、x₄、x₅分别是影响波峰焊点焊质量的焊锡液面高度、轨道倾角、波峰宽度，在控制图分析的过程中可以获悉，轨道倾角的极差图总是有连续9点在中心线同侧，这可能是由于在用角度规测试读取数时存在着人为地读数误差；波峰宽度和焊锡液面高度是用专用仪器测量，读取数据较精确，可以从专用仪器感知轨道倾角方面来提高轨道倾角的准确性，但是也要注意仪器的保护，避免仪器疲劳导致测量不准确。

步骤3 多变量过程能力指数计算

这里仍采用规范区域为长方形的多变量过程能力的计算公式。分布中心与规范中心不重合。

进而求得：

最后得到修正的过程能力指数为1.0196。根据表1过程能力评定标准，仿真过程处于基本稳定状态，但过程能力一般。应该在保持现有生产情况下，继续用控制图或其他有效手段对过程进行严格监督和控制，严格检查产品质量，防止出现过程能力大幅下滑。就单个变量而言，x₃需要强化质量控制检验、分析变异原因，进而采取有效的措施；x₄處于一个理想状态，需要继续保持；x₅处于一种中风险状态，需要增加检验频次，找到变异原因并消除，提高过程能力值。

分别对原始数据和多容量组数据采用几何平均法、差异系数法、规范区域为长方形修正法的多变量过程能力指数进行计算。表4对各种多变量过程能力指数计算方法进行了比较。

由表4可知，几何平均法计算的多变量过程能力指数比采用差异系数法和规范区域为长方形的修正法要大。几何平均法是一种早期求解多变量过程能力指数的计算方法，其计算求得的过程能力指数值偏大，不太适合多变量过程能力指数的求解。本文采用的规范区域为长方形的修正法，计算结果跟差异系数法求得结果比较接近，也最接近真实的实际情况。同时，本文针对原始子组容量为1的数据计算结果与随机生成的子组容量为5的仿真计算的多变量过程能力指数进行了对比，对比结果除了几何平均法误差较大外，其余两种计算方法基本一致，这也说明随机生成的数据是有效的，而多容量样本分组也是多变量质量控制图的要求。

3 结论

本文采用规范区域为长方形的修正法计算了生产过程能力指数，通过案例研究对控制图和过程能力指数的分析，使得工序过程一直处于统计受控状态，以提高产品质量。

1）多变量T²、MEWMA控制图能较好地对工序状态进行诊断，及时发现过程异常波动，并能对工艺过程质量进行初步分析，找出其中失控的原因。

2）多变量过程能力指数计算方法很多，但早期根据单变量过程能力指数采用几何平均法求得的多变量过程能力指数偏大，会影响生产过程能力的判断。本文采用规范区域长方形修正法计算多变量过程能力指数误差较小，能有效监督和控制生产过程。

[ 参 考 文 献 ]

[1] 蒋家东，冯允成. 基于协方差阵特征结构的新型控制图研究[J]. 中国管理科学，2011，19（06）：123-133.

[2] NIJHUIS A，JONG S D， VANDEGINSTE B G M . Multivariate statistical process control in chroma to graphy[J]. Chemometrics and Intelligent Laboratory Systems， 1997， 38：51-62.

[3] WU C W， PEARN W L， KOTZ S. An overview of theory and practice on process capability indices for quality assurance[J]. International Journal ofProduction Economics， 2009， 117： 338-359.

[4] TAAM W， SUBBAIAH P， LIDDYY J W.A note on multivariate capability indices[J]. Journal of Applied Statistics， 1993， 20（03）： 339-351.

[5] AHMAD S， ABDOLLAHIAN M， ZEEPHONGSEKUL P， et al. Multivariate nonnormal process capability analysis[J]. The International Journal of Advanced Manufacturing Technology， 2009， 44：757-765.

[6] 罗碧青，蔡良平，黄玲，等.过程能力指数在粉末直压工艺研究中的应用[J].食品安全质量检测学报，2020，11（24）：9548-9554.

[7] SHABAN A， SHALABY M， ABDELHAFIEZ E， et al. Automated identification of basic control charts patterns using neural networks[J]. Journal of software Engineering and Applications，2010，3（03）：208-220.

[8] 郭佳晟，刘以建.基于非参数统计量的多元控制图研究[J].组合机床与自动化加工技术，2021（09）：122-124.129.

[9] GUH R S. Simultaneous process mean and variance monitoring using artificial neural networks[J]. Computers and Industrial Engineering，2010，58（04）：739-753.

[10]汪洋，陈向东，闪四清. 基于ARL的T2控制图多元质量特性统计设计经济模型[J]. 工业工程，2013，16（04）：133-39.

[11]赵凯. 多元制造过程能力分析及质量诊断[D].天津：天津大学，2011.

[12]孙静，王胜先，杨穆尔. 过程能力分析[M].北京：清华大学出版社，2013.

[13]孙红日，林国辉. 波峰焊常见问题及解决对策[J].电子工艺技术，1999，2（05）：185-186.

[14]周志近. 波峰焊工艺及常见问题分析[J]. 现代显示，2009，16（02）：61-63.

Research on Multivariate Control Chart and Process Capability

Index Applied for Manufacturing Process

LEI Binwen¹，GONG Lixiong²

（School of Mechanical Engineering， Hubei Univ. of Tech.， Wuhan 430072， China）

Abstract：Aiming at problems that single control charts cant accurately find and diagnose small swing of process， the paper proposed to joint multivariate T² and MEWMA control chart to diagnose manufacturing process state， and judged the production process state by multivariate process capability index. First， it analyzed multivariate T² and MEMWA control chart & revision process capability index that norm district is rectangular， and then targeted at an electronic enterprise motherboard controller manufacturing process， focused on the analysis of factors affecting welding process quality. Moreover， it proposed method that jointed multivariate T²and MEWMA control chart & process capability index diagnosed production state， respectively analyzed influencing factors of process quality. Result shows that the multivariate quality diagnose error proposed in the paper is small， and can effectively monitor and control manufacturing process.

Keywords：Multivariate control chart；Process capability index；Manufacturing process control；MEMWA chart；Quality diagnosis

[責任编校：张 众]