Assessing edge-coupled interdependent network disintegration via rank aggregation and elite enumeration
2023-12-02YongHuiLi李咏徽SanYangLiu刘三阳andYiGuangBai白艺光
Yong-Hui Li(李咏徽), San-Yang Liu(刘三阳), and Yi-Guang Bai(白艺光)
School of Mathematics and Statistics,Xidian University,Xi’an 710071 China
Keywords: edged-coupled,rank aggregation,interdependent networks,elite enumeration
1.Introduction
Complex networks are ubiquitous in modern society,[1]encompassing a wide range of systems such as power grids,communication networks, and social networks.As technology advances, these networks are becoming increasingly intertwined and their structures are growing more complex.[2–5]Therefore, gaining a comprehensive understanding of the intricate association patterns within and between these networks is crucial for in-depth analysis.
Extensive research has been conducted on robustness of single-layer networks, including the identification of key nodes[6–12]and edges.[13–15]However,with the increasing interconnectivity of networks,single-layer models are no longer sufficient to meet practical needs.In reality, interdependent networks are more prevalent, such as cyber-physical power systems (CPPSs) and financial networks composed of different regions.Although current research on interdependent networks is based on point-to-point coupled networks,[16,17]which establish links between layers through individual nodes,many real-world interdependent networks rely on edge-toedge coupling.For instance, city networks comprise many cities connected by transportation routes.Another example is the edge-coupled network of the transportation network and economic trade network, where the trade relations between economies depend on the routes in the transportation network.As well as the edge-coupled network of production supply chain network and logistics and transportation network where suppliers need logistics services for distribution and transportation of goods, etc.Despite the prevalence of such edgecoupled interdependent networks, there is a lack of in-depth research on their robustness, resulting in limited understanding of the impact of edge failures in one network on another network.Therefore,studying the robustness of interdependent networks based on edge-coupled links is critical.
Real-world networks exhibit heterogeneity, where a few nodes and edges play crucial roles in determining network structure and function,while the majority of nodes and edges are less significant.Numerous methods have been developed to identify key nodes, such as degree centrality, betweenness, andk-core decomposition.For instance, Xuet al.[18]proposed an information entropy-based algorithm that considers two-hop information to identify key nodes.Wanget al.[19]developed a multi-scale information importance method that integrates local and global information to identify critical nodes more effectively.However,few studies have focused on identifying significant edges in networks, but it is also critical to network disintegration and protection.For instance, in CPPSs,[20]identifying critical transmission lines can help prevent possible attacks and reduce the likelihood of cascading failures in interdependent networks.Similarly, in infectious disease networks, breaking the most damaging transmission chains by identifying critical edges can prevent further disease spread.Consequently,this paper investigates the robustness of edge-coupled interdependent networks by examining the critical edges in the network.
Identifying the significant edge sets in the network has been proven to be NP-hard (non-deterministic polynomial),indicating that it is a non-deterministic polynomial-time problem.Therefore,the resolution of this combinatorial optimization problem necessitates the development of innovative and efficient algorithms.The time cost can be high when choosing methods such as intelligent optimization to search for significant edge sets.Therefore, our goal is to make the proposed algorithms achieve a satisfactory balance between effectiveness and efficiency as much as possible.Compared with pointcoupled networks,edge-coupled networks are more robust and less prone to disintegration,so how to effectively disintegrate edge-coupled networks is novel and well worth considering.Therefore,edge-coupled networks under one-to-one links are chosen as the object of the present study.
To improve efficiency and effectiveness,a novel rank aggregation elite enumeration algorithm based on edge-coupled networks(RAEEC)is proposed.Our algorithm performs rank aggregation of multiple edge importance metrics,avoiding the one-sidedness of single metrics and the high time cost of intelligent optimization algorithms.The conversion of large enumeration to small enumeration in selecting the set of elite attack edges saves time and cost significantly.Extensive experiments are conducted on synthetic networks,and results show that our new method outperforms existing state-of-the-art algorithms.The main contributions of this study are as follows:(1)Model one-to-one interdependent edge-coupled networks.(2)Implement to combine metrics with different layers of edge importance into one.(3) The RAEEC algorithm achieves a satisfactory balance between effectiveness and efficiency.
The rest of this paper is organized as follows.Section 2 presents recent advances in the study of the importance of edge nodes.The basic definition of complex networks is given in Section 3, and advanced metrics for studying edge importance are presented.Section 4 gives the model of edge-coupled interdependent networks under one-to-one links and the process by which cascading occurs.In Section 5,we propose the RAEEC algorithm for identifying the significant edges in the network.Section 6 presents the results of simulation experiments and compares the RAEEC algorithm with four stateof-the-art algorithms.Finally, in Section 7, conclusions are drawn based on our findings.
2.Related works
In recent years, there has been an increasing interest among researchers in identifying important edges in a network due to their significant practical applications.Most of the current methods for measuring the importance of edges rely on the structural information of the network.
The concept of edge meson,which is a generalization of the point meson, has been proposed, but it requires a large amount of computational resources.Similar to the betweenness of nodes, the edge betweenness[21]was proposed by Newmanet al.Yuet al.[22]proposed the BCCMOD algorithm based on the number of edge networks,which takes into account the topology and information dissemination capability of the network.However,all of these algorithms are based on global information and perform better on small-scale networks, but are not suitable for large-scale networks.To address this issue,Holmeet al.[23]introduced the concept of degree product(DP),where the DP of an edge is the product of the degrees of the two endpoints of the edge.Chenet al.[24]proposed a semi-local centrality metric (SLC) that considers information from one-, two-, three-, and four-hop neighbors and works better than some global centrality indices on most real networks.
Chenget al.[25]have proposed the Bridgeness metric to quantify the importance of edges in maintaining network links.Liuet al.[26]have introduced diffusion intensity(DI)as a measure to explain the diffusion of edges in dynamics, and Zhaoet al.[27]have proposed a second-order neighborhood(SN)index that accounts for the topological overlap (TO)[28]of the second-order neighbors of the two endpoints of an edge.Additionally, some methods have investigated the importance of edges, including eigenvalues,[29]nearest neighbor links,[30]and so on.
Intelligent optimization algorithms, such as evolutionary algorithms[31]and tabu-search algorithms,[32]can also be used to find significant edges in the network.However,while these algorithms may yield better results compared to centrality algorithms,their time complexity is generally very high.Therefore,achieving a balance between efficiency and effectiveness is a critical issue.
While previous algorithms for identifying significant edges in networks are based on single-layer networks,for edge-coupled interdependent networks, considering only intra-layer neighborhoods can result in a loss of significant information.Thus,this paper improves previous algorithms for edge-coupled interdependent networks and proposes a novel algorithm that balances effectiveness and efficiency to achieve a satisfactory trade-off between the them.
3.Preliminaries
The interdependent networks consisting of two networks are abstracted as an undirected, unweighted graphGA:=(VA,EA),GB:=(VB,EB),respectively.NA=|VA|andNB=|VB|are the numbers of nodes in networksGAandGB;EAandEBis the sets of edges in the networks.We describe the networksGAandGBby adjacency matricesAandB,respectively,whereaij=1 andbij=1 indicate the direct existence of links between nodesiandj, otherwiseaij=0 andbij=0.In this section, four advanced metrics used to measure edge importance are presented.
3.1.Degree product
The degree product (DP) is expressed as the product of the degrees of nodesiandjat the ends of edgeei j,
wherekiandkjare the intra-layer degrees of nodesiandj,respectively.
3.2.Topological overlap
To measure the topological overlap(TO)of two vertices in an edge, we introduce the concept of topological overlap.A smaller value of topological overlap means that the edge is more important,
wherekiandkjdenote the degrees of nodesiandj,ni jdenotes the number of common neighbors of nodesiandj.If nodesiandjdo not have any common neighboring nodes, thenni j=0, implying that the value ofT(i,j) is also zero.If the common neighbors of nodesiandjare identical,T(i,j)=1.
3.3.Diffusion intensity
Diffusion intensity(DI)is the average of the propagation intensity of nodesiandj,
whereni/jis all neighbors of nodeiminus those remaining neighbors associated with nodej, andnj/iis all neighbors of nodejminus those associated with nodei.TheI(i,j) metric quantifies the average potential impact of edgeei jin both directions(i →j,j →i).
3.4.Second-order neighborhood index
The second-order neighborhood (SN) index shows the topological overlap of the second-order neighbors of the two endpoints of an edge,and the index is considered an extension of the topological overlap index.Similar to topological overlap, the lower the SN value is, the more important the edge is,

4.Edge-coupled one-to-one interdependent networks
4.1.Definition of edge-coupled interdependent networks
In this paper,we consider a two-layer edge-coupled interdependent network under one-to-one links,where the two layers are denoted as networkGAand networkGB, and assume that a node in networkGAcan have at most one dependent edge in networkGB.
To visualize the edge-coupled network with one-to-one links, a specific example is shown in Fig.1.The interdependent network in the figure consists of two networks,GAandGB, with eight nodes inGAand eight nodes inGB, respectively.GAandGBcontain 9 and 8 edges,respectively,with at most one coupling edge existing at each node.BothGAandGBare maximal connected branches,so the edge-coupled network consisting ofGAandGBalso forms a giant component.
Since the coupling relationship between the layers is edge-coupled, using a symmetric adjacency matrix to record the coupling edges is not reasonable.For edge-coupled networks,we need to record the edges ofGAandGBcorresponding to the coupling edges in two separate matrices.For convenience, we define the matrixDto describe the inter-layer coupling edges.Its dimension isn-by-4, wherenrepresents the number of coupling edges andn ≤min(|EA|,|EB|).The first two numbers in each row of matrixDrepresent the node numbersiandjof the edges inGAfor which the coupling edge is coupled,and the last two numbers represent the node numbersi′andj′of the edges inGBcorresponding to the coupling edge.
4.2.The propagation process of cascading failures
In this paper,we presume that only edges in layerGAare attacked and that layersGAandGBhave the same cascade pattern after a failure.When an edge in layerGAis attacked,that edge is immediately disconnected, and at the same time,if there is a coupled edge in that edge, the edge in layerGBto which it is coupled is also disconnected.Next, a cascade failure may occur in the interdependent network, simply by finding the maximum connected branches of layersGAandGBrespectively, and then continuously deleting edges and nodes until the cascade failure ends.
We presume the ratio of the number of nodes belonging to the giant component in the network at the end of the cascade failure to the total number of initial nodes is used as a measure of the robustness of the edge-coupled interdependent network,denoted byS(Q), whereS(Q)=(N′A+N′B)/(NA+NB).Qis the edge set of the attack, andN′AandN′Bare the numbers of nodes remaining in the networkGAandGB,respectively,after the attack and the cascade occurs.

Fig.2.A concrete example of a cascading failure in an edge-coupled network.Layer GA and GB are a pair of one-sided couplings, with solid black lines indicating edges connecting nodes belonging to the giant component of each layer and vertical dashed lines indicating coupled edges between layers.Attack edge a3–a4 in layer GA, the final percentage of nodes remaining in the interdependent network is S(Q)=(5+4)/(7+7)=0.64.
•First stage: In layerGA, edgesa3–a4are invalidated due to deliberate attacks, and since layers,GAandGBare one-to-one coupled,edgesb4–b5are removed from layerGB,while the coupled edges linkinga3–a4andb4–b5are removed.
•Second stage: Find the giant component in theGAlayer and delete the edgea4–a5.Next, find the edgeb4-b7coupled to the edgea4–a5in theGBlayer and delete it.
•Third stage: Similar to the second stage, find the edge in layerGBthat does not belong to the giant component and delete the edgeb5–b6,while finding the edgea3–a7coupled with the edgeb5–b6in layerGAand delete it.
•Fourth stage: Repeat the steps in the second and third stages to delete nodes and edges inGAandGBthat do not belong to the giant component until all nodes and edges belong to the giant component, ending the cascade.
Our goal is to maximize the degree of disintegration of the interdependent network by attacking edges in networkGA.In this paper,we consider an edge-coupled network measured by the proportion of remaining nodes in the network denoted byS(Q).Therefore,the problem of minimizing the maximum number of giant component (MIN-GC) of the edge-coupled networks can be formulated as follows:
wherevkindicates whether thek-th edge is selected,vk=1 means that thek-th edge is selected into the attack edge set,vk=0 means that it is not selected, andf(0≤f ≤1) indicates the deliberate attack strength.
5.Rank aggregation elite enumeration algorithm for disintegrating edge-coupled networks
5.1.Definition of rank aggregation method
To facilitate the study, this paper chooses to attack only the edges in networkGA.For the importance of edges in networkGA,we need to consider also the possible coupled edges between networkGAand networkGB.Taking the edge diffusion strength as an example of a measure of edge importance,the idea of this paper is to assume that any edgeei jis chosen in-networkGAand if there is a coupling edgeeijbetweenei′j′ and networkGB,then the overall diffusion strength of that edgeeijis
whereIA(eij)andIB(ei′j′)are the diffusion intensity values ofGAandGBat the network layer.
Since the coupling between networksGAandGBis oneto-one when an edgeeijin networkGAis attacked, if a coupling edgeei′j′exists for that edge,then edgeei′j′will also be removed from networkGB.Therefore, the importance of an edge in networkGAshould be measured by adding the edge in networkGAthat is coupled to that edge.
In order to maximize the disintegration of the network,we need to find the optimal set of attacking edges such that the combination of this set of attacking edges hurts the coupled edge network the most.Previous studies on the importance of nodes have many measures, including degree, betweenness, and so on.In fact, if we use only one criterion to measure node importance, we are likely to miss some potentially critical nodes.This is true for nodes as well as for edges.For single-layer networks,the graph-based rank aggregation method[33]aggregates all individual rankings into a single consensus ranking.Therefore,in this study,by combining several more advanced methods for studying the importance of edges in networks,we propose an RAEEC algorithm based on edge-coupled interdependent networks.
ConsiderNrepresentatives{r1,r2,...,rN}ranking|EA|edges in networkGAsequentially, and the obtained ranking matrix is set toR=(ri j)N·|EA|, whereri jdenotes the ranking after the scoring given to thej-th edge by representativeri.A concrete example of rank aggregation is given in the following:
where each row inRdenotes the ranking of each edge after the representative personriscores, respectively.Matrix(7)gives the ranking of the six representatives scoring the five edges.Take the first row of theRmatrix as an example,the five edges are ranked as 4,3,5,1,and 2.
A transition matrixTi=(tjk)|EA|·|EA|(1≤i ≤N) is obtained below from each row ofRseparately.Ifrijis smaller thanrik,it means that thei-th representative considers the edge numberedjmore important than the edge numberedk, i.e.,tjk=1,otherwise,tjk=0.

Finally, we can define a measure of the importance of edges in networkGAby calculating the ratio of incoming and outgoing edges(RIOE)as follows:
The three parameters and the final ranking of each edge are listed in Table 1.The overall ranking of the edge set from front to back ise5,e4,e3,e2,e1.The final rank aggregation based on edge coupling is ranked as ˆR=[e5,e4,e3,e2,e1].
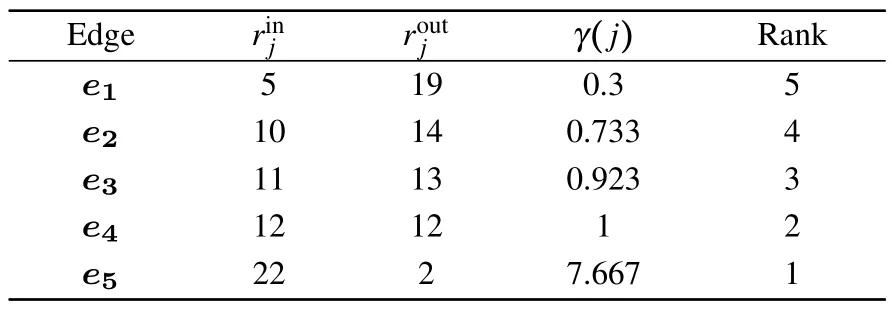
Table 1.Final ranking results of the edge set based on the rankaggregation method.
5.2.Rank aggregation elite enumeration algorithm
In the following, we will propose a novel rank aggregation enumeration algorithm.First,the rank aggregation is performed forEAedges in the network layerGAaccording to the previously proposed method.Based on the extensive experimental analysis,it is found that the best result is achieved whenN=3.Too few or too many indicators will affect the effect of aggregation.The metrics chosen in this paper are HDI,[26]HTO,[28]and HSN.[27]
The HDI, HTO, and HSN methods differ from the DI,TO, and SN methods in that each time.The most significant edge in the current network is determined, that edge is removed from the network.The above steps are repeated until all edges in the network are sorted.It is not difficult to infer that the HDI, HTO and HSN methods can dismantle the network to a greater extent under the same attack strength because it avoids repeated attacks and improves the attack efficiency.
Our approach is to select the optimal set of edgesIamong the three methods HDI, HTO and HSN and to take the highest ranked part of edges in the rank aggregation and merge them.Suppose that the attack strength isf, i.e., the number of edges attacked at this point isf·|EA|,and then the optimal set of edges among the three methods and the top-ranked set in the rank aggregation method are selected and merged, respectively, to obtain 2·f·|EA| (|I|=2·f·|EA|) edges as the candidate edge set.Next, the set of candidate edges is enumerated, but if we perform a simple one-by-one enumeration of the setI,i.e.,takeit is not difficult to find that the time cost must be very high.



Fig.3.The process of entering the queue of attack edge sets.
The RAEEC algorithm based on edge-coupled interdependent networks for solving the set of attacking edges can be summarized in the following five steps:
Step ICalculate the HDI, HTO, and HSN values of all edges in the network layersGAandGBcorresponding to the three metrics.
Step IIIf edgeiin networkGAhas coupling edgejin networkGB, the importance value corresponding to edgeiis equal to the importance value of edgeiplus edgejin the previous step.
Step IIIUsing the three indicators HDI, HTO, and HSN as representatives, the score matrixUis calculated using the rank aggregation method, and the importance ranking of all edges in networkGAis obtained.
Step IVUnder the condition that the attack intensity isf,perform a queuing operation onf·|EA|edges,with each group of five edges.Enumerate the union sets of the top 5 edges obtained from the best of the three algorithms and rank aggregation, queue the best solution inCk′j, and delete the queued edges in the network.
Step VRepeat step IV until all thef·|EA|edges are in the queue,thef·|EA|edges are the set of elite attack edges.
6.Simulation results and analysis
We conducted extensive numerical experiments on synthetic and real networks and compared the RAEEC algorithm proposed in this paper with four classical methods for computing edge importance to verify the advantages of the RAEEC algorithm.The four compared algorithms are the high degree product(HDP),[23]the high topological overlap(HTO),[28]the high diffusion intensity (HDI),[26]and the high second-order neighborhood index(HSN).[27]
All the experiments listed in this paper were performed on a Windows 11 computer with an Intel i7-12700 CPU and 16 GB of RAM,implemented under MATLAB 2020b.
6.1.Benchmark datasets
In this section, three representative artificial networks,i.e.,BA scale-free networks,[34]ER random networks,[35]and small-world (WS) networks[36]are chosen for comparisons.The edge coupling between networksGAandGBis chosen in this paper to be a random one-to-one link,with at most one dependent edge in the network that exists in the other network.The details are as follows.
ER networksEach layer in the network is defined by two parameters:Nandp, i.e.,pis the probability of connecting each pair of nodes andNis the number of nodes in the network.In this paper, we setNA,NB=50, 80, 100, 200 andp=0.12, 0.08, 0.06, 0.03.The final edge-coupled ER-ER network includes 100,160,200 and 400 nodes.
BA networksGenerating a scale-free network requires three input parameters:m0,m, andN.The initial number of vertices in each layer of the network ism0, andmedges are added for each additionalyvertices until the number of nodes in the network isN.For extensive experiments,we setNA=NB=50, 80, 100, 200,m0=5, andm=3.The final edge-coupled interdependent network includes 100,160,200,and 400 nodes.
WS networksThree parameters are required to generate the WS network,Nis the number of points,Krepresents the total number of neighbors per node, where the left side hasK/2 neighbors and the right sideK/2 neighbors,andprepresents the reconnection of each edge in the network with probabilityp.For extensive experiments,we setNA=NB=50,80,100,200,p=0.02,andK=6.
Although the above three networks are artificially generated, they contain many features of complex networks and can be studied as the topology of real social relationships.BA scale-free networks are highly heterogeneous,as evidenced by the preferential connection mechanism of their nodes.Reallife social, biological, and trade networks all have the characteristics of scale-free networks.ER networks are homogeneous,and small-world graphs reflect a characteristic of friend networks.To diversify the experiment, we coupled different networks for comparative study.
6.2.Experiments and results
In this paper, we assume that the network has achieved disintegration when the proportion of remaining nodes in the coupled network is less than 20%.For comparative analysis,the intra-layer average degree of BA, ER and WS is set to 6,while networksGAandGBare generated separately.
Figure 4 shows the total number of nodes in the network for 100, 160, 200, and 400, respectively.It can be seen that all RAEEC algorithms outperform the four advanced methods mentioned above in identifying the significant edges of the network.In the first half of the curve,the RAEEC algorithm does not differ much from HDI,HTO and HSN,but as the percentage of attacks increases, the advantage of RAEEC becomes more obvious.
The slope of the curve in the figure becomes steeper and steeper.When the attack intensity is small, the overall damage to the edge-coupled network is small, and the curve falls more gently, attacking roughly 40% of the nodes in the network.However, as the attack intensity increases, the edges connected to the vertices are removed one after another, and cascade failures occur continuously within the network layer.If there are inter-layer coupled edges,the cascade will also occur within another layer, which leads to the proportion of remaining nodes dropping directly from 60%to less than 20%.
According to the theoretical analysis,the BA-BA network should be the easiest to disintegrate because its heterogeneity is the strongest.However, in Fig.4, it is not difficult to find that the WS-WS edge-coupled network is the easiest to disintegrate.We analyze it because in this paper only the WS-WS network fully implements one-to-one inter-layer coupling,i.e.,attacking the edges in the networkGA, it must be possible to find coupled edges connected in the networkGB,making its attack effect be better.The average degree of the remaining two coupled networks is only approximately equal to 6, i.e., the neighboring edges of networksGAandGBare not equal,which leads to the WS-WS network being easier to disintegrate compared to ER-ER and BA-BA.Secondly, the BA-BA network is more prone to disintegration with a percolation threshold equal to 0.7 less than the ER-ER network.The ER-ER edgecoupled network is the lowest degree of disintegration among the three coupled networks, and its percolation thresholdfcremains around 0.8.
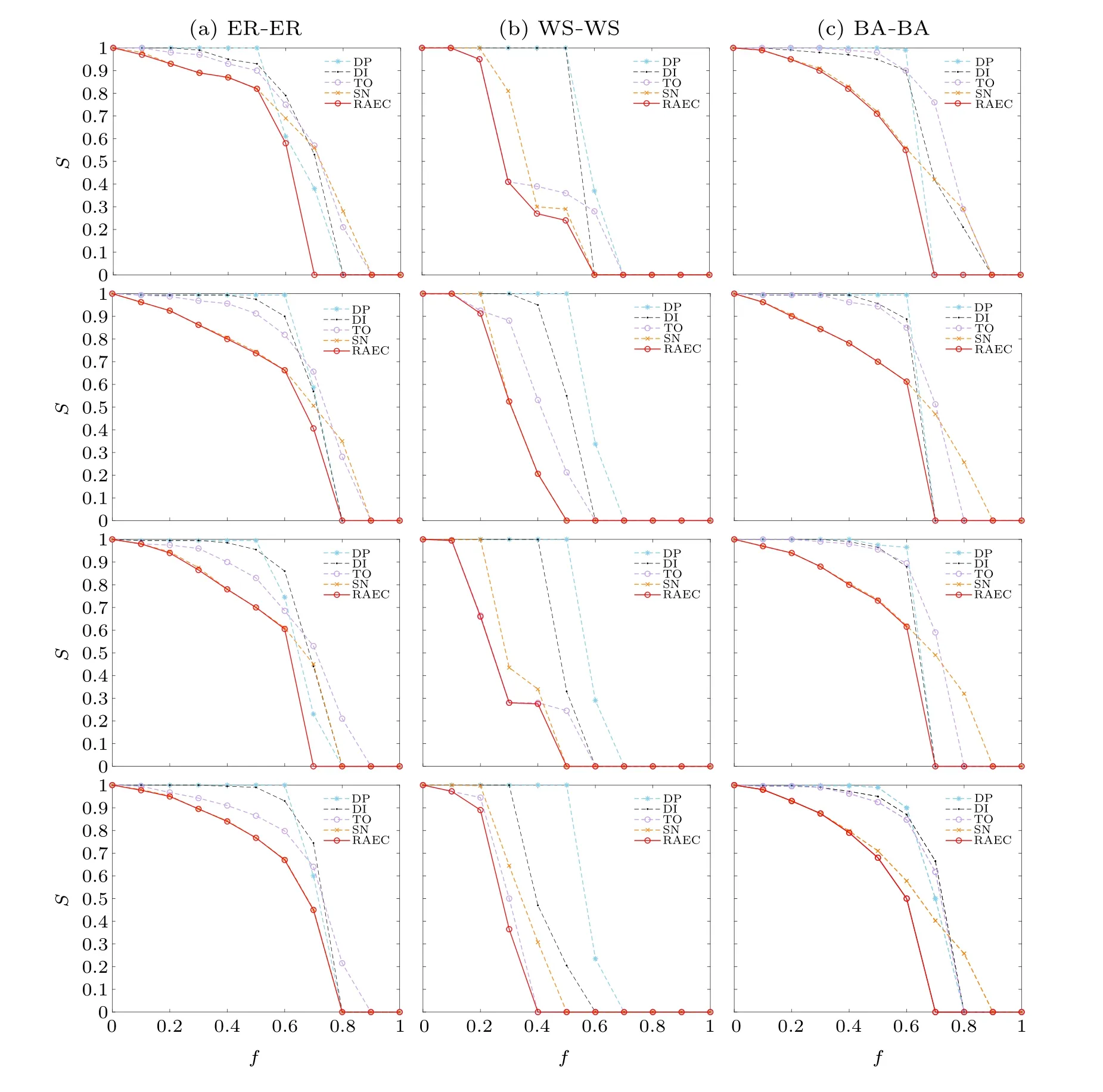
Fig.4.Comparisons of different methods under edge-coupled interdependent networks.The four rows indicate the total number of nodes in the network as 100(NA=NB=50),160(NA=NB=80),200(NA=NB=100),400(NA=NB=200).

Fig.5.Comparisons of different methods under ER-BA,BA-ER,and BA-WS edge-coupled interdependent networks.The three rows indicate the total number of nodes in the network as 100(NA=NB=50),160(NA=NB=80),200(NA=NB=100).

Fig.6.Comparisons of different methods under WS-BA,ER-WS,and WS-ER edge-coupled interdependent networks.The three rows indicate the total number of nodes in the network as 100(NA=NB=50),160(NA=NB=80),200(NA=NB=100).
From Figs.5 and 6, it can be seen that the RAEEC algorithm combines the advantages of HDI,HTO and HSN and outperforms all four compared algorithms.The shapes of the curves are roughly similar as the number of nodes in the network increases.Meanwhile,when the number of nodes in the network is the same,the ER-BA edge-coupled network is less robust, and its percolation threshold is all 0.7, which is more easily disintegrated compared with the BA-ER coupled network.Therefore, when the disintegration cost is limited to choosing one of BA and ER to construct the edge-coupled network, we choose the networkGAas the ER network.This is because the edge-coupled network can be disintegrated more efficiently for the same attack ratio.
For the edge-coupled networks with different upper and lower layers consisting of BA and WS, the WS-BA network is less robust,and its percolation thresholds are all below 0.7.Meanwhile,compared with the BA-WS network,the RAEEC algorithm has more obvious advantages over the remaining four compared algorithms.For the edge-coupled network composed of ER and WS,the WS-ER edge-coupled network is less robust and has a larger drop in the curve compared to the ER-WS network.
Compared with the ER-ER edge coupling in Fig.4, replacing the networkGBfrom ER network with the BA network reduces the robustness of the network and is more prone to disintegration.In contrast,replacing the networkGAwith the BA network reduces its robustness but does not change much,and its percolation threshold remains around 0.8.
We selected three larger-scale edge-coupled networks,WS-WS (NA=NB=600,〈kA〉=〈kB〉=4), WS-WS (NA=NB=1000,〈kA〉=〈kB〉=2), and BA-BA (NA=NB=2000,〈kA〉=〈kB〉=4),for our experiments.From Fig.7,it is easy to find that the RAEEC algorithm still outperforms the remaining four comparative algorithms on the larger-scale networks,indicating that the algorithm has effectiveness and stability.

Fig.7.Comparisons of different methods on larger scale edge-coupled networks.Three represent the total number of nodes in the network as 1200(NA=NB=600),2000(NA=NB=1000),and 4000(NA=NB=2000).
6.3.Time complexity and runtime
In the following, we analyze the time complexity of the five algorithms.For the four methods DP,DI,TO,and SN,the time complexity isO(|EA|·N2A).
Now we analyze the time complexity of the RAEEC algorithm proposed in this paper.First,it is necessary to calculate the edge importance ranking of the three algorithms DI, TO,and SN, respectively, whose time complexity isO(|EA|·N2A).Next,ranking aggregation is performed to obtain the combined ranking of the set of edges of networkGAwith time complexityO(|EA|2).Finally, elite enumeration is performed, with a time complexity ofIn summary,the time complexity of the RAEEC algorithm isO(|EA|2·N2A).
Although the time complexity of the RAEEC algorithm is slightly higher than the remaining four previous comparison algorithms,the results of RAEEC are significantly better than the four algorithms.Compared with intelligent algorithms,RAEEC does not need the repeated variation and crossover mechanisms in intelligent algorithms to maintain the improvement of results and has obvious efficiency advantages.Therefore, the RAEEC algorithm obtained by rank aggregation of three algorithms HDI, HTO and HSN, and elite enumeration achieves a balance in efficiency and effectiveness directly.
For the running time of these five algorithms, we conducted experiments on BA-BA edge-coupled network,and the results show that when the number of network nodes is 100,the running time of the DP algorithm is 1.29 s, the running time of the DI algorithm and TO algorithm are similar,which are 3.51 s and 3.39 s,respectively.For the SN algorithm it is 30.11 s,and for the RAEEC algorithm proposed in this paper it can be seen that the running time of the RREEC algorithm is close to that of the SN algorithm,but the effect is much better than that of the SN algorithm.
7.Conclusion
This paper presents a method to disintegrate edgecoupled interdependent networks by attacking the set of significant edges in the networkGA.A rank aggregation elite enumeration algorithm is proposed.First,the combined ranking of all edges in networkGAis obtained by the rank aggregation method.Next, the enumeration set is determined and the best of the three algorithms in HDI, HTO, HSN, and the top-ranked edges obtained by the rank aggregation algorithm is selected.The enumeration set is enumerated one by one in the group, and the best edge set in the group is entered into the queue, and the cycle continues so that the edge set is entered into the queue until the condition is satisfied.Compared with direct enumeration, RAEEC can greatly reduce the time complexity.The set of attack edges obtained at the same time combines the advantages of all three methods,HDI,HTO,and HSN,under different attack strengths,and the results are better than all the three methods.
Extensive experiments have been conducted on synthetic networks,and the results show that the elite edge sets obtained by RAEEC are superior to the three methods of HDI, HTO,and HSN, and their time complexity is not significantly different.Moreover, the time complexity of RAEEC is greatly reduced compared to evolutionary algorithms,etc.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant Nos.61877046, 12271419,and 62106186), the Natural Science Basic Research Program of Shaanxi (Program No.2022JQ-620), and the Fundamental Research Funds for the Central Universities (Grant Nos.XJS220709,JB210701,and QTZX23002).
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- The application of quantum coherence as a resource
- Special breathing structures induced by bright solitons collision in a binary dipolar Bose–Einstein condensates
- Effect of short-term plasticity on working memory
- Directional-to-random transition of cell cluster migration
- Effect of mono-/divalent metal ions on the conductivity characteristics of DNA solutions transferring through a microfluidic channel
- Off-diagonal approach to the exact solution of quantum integrable systems
