基于MALAB的概率统计实验教学探析
2023-12-01周宗好王佳佳
周宗好,王佳佳
(黄山学院数学与统计学院,安徽 黄山 245041)
0 引 言
概率论与数理统计作为研究随机现象统计规律性的重要课程,从不确定性视角为人们提供了认识世界的思维方式以及分析问题的思路方法,其中所蕴含的统计思维是大数据时代公民所必备的核心素养之一[1]。但在教学实践中,学生普遍反映课程的理论性强,内容抽象,公式繁密且枯燥深奥,这导致很多学生常常望而生畏,核心知识技能目标达成度不高。因而,基于“两性一度”金课标准下学生学习痛点的解决是本课程教师亟需思考的核心问题之一[2]。
随着MALAB软件等信息技术与公共数学教学融入进程的不断推进,不仅有效地促进了数学课堂教学方式的变革,也为学生的数学学习提供了丰富的环境与资源[3]。这一优势在概率论与数理统计课程教学中尤为明显,由于概率统计课程的研究对象为随机现象统计规律性,若依靠黑板、粉笔等传统教学手段很难即时实现对随机数的生成以及对不同层次数据的统计分析,这不仅不利于学生对随机事件的统计规律性理解,也不能有效地促进学生积累数据分析的经验[3-5]。因而,在教学时可以借助计算机并引入MALAB 以及R 软件等开展诸如蒲丰投针等各种模拟活动,并对城市经济社会等领域产生的大样本数据进行处理、描绘与分析,促使学生能够在借助软件完成概率统计的相关计算、统计分析及统计推断的基础上理解与体会概率的意义以及统计的思想,也为学生统计思维与素养的形成奠定基础[6,7]。本教学团队针对学生概率统计学习的痛点,围绕促进学生深度学习以及统计思维形成的教学目标,引入MALAB 软件在统计实验中应用并展开了系列创新教学探索。
1 教学内容的可视化
随着信息技术的发展,“数学可视化”作为近几届数学教育心理学国际研讨组(PME)的热点主题之一。数学可视化即是将抽象的数学学习对象运用图形、图象、动画等“可看得见、清楚呈现”的表征形式进行呈现,促使人们对数学学习对象有一个形象、直观、整体的认识和理解。学情分析表明,概率论与数理统计课程中诸多概念与定理的抽象程度较高,由于学生概率统计理论缺少直观认知,很容易对概念本质理解产生困难或错误。这不仅影响了学生的学习进度与效率,长此以往也会降低学生的学习兴趣。例如,概率密度函数作为概率论中的核心概念之一,是描述连续随机变量概率分布的主要工具[8]。但由于其在定义上与前面所学的概率分布函数有相似之处,且学生对分布律的认知经验较少。因此,为了更好地帮助学生能够正确地把握分布律的思想方法,辨析与其他相关概念的差异,在教学中可以借助MALAB软件的图形表示处理与直观演示功能,将类似各类概率分布等抽象概念借助图象进行可视化,引导学生对表达式中的关键参数进行观察、比较与理解,从而准确快速理解相关内容。
例1:利用MALAB 软件分别绘制参数μ= 2、σ2= 2, 3, 5的正态分布的概率密度函数。
绘制图形程序为:
clear all; clc
x=-10:01:14;
norm1=normpdf(x,2,2);
backColor=[1, 0.9 0.9];
plot(x,norm1,'k-','LineWidth',2);
set(gca,'ytick',0:0.04:0.2,'xtick',-10:4:14,'Font-Size',10,'TickLength',[0.01,0.01],'color',backColor);
axis([-10 14 0 0.2]);
grid on;
xlabel('x', 'FontSize', 10); ylabel('f(x)', 'Font-Size',10);
hold on;
norm3=normpdf(x,2,3);
plot(x,norm3,'b-','LineWidth',2);
hold on;
norm5=normpdf(x,2,5);
plot(x,norm5,'r-','LineWidth',2);
legend('sigma^2=2','sigma^2=3','sigma^2=5')
通过引导学生对本题中不同参数取值的图形进行观察、比较与讨论,促使学生能够在比较中理解σ2为位置参数的含义,感知其图像对称性以及参数的变化对图象影响的作用等重要性质以及概率密度函数的概率意义。同时在课后还能继续组织学生借助MALAB软件对概率分布函数的图象进行探索,通过对两概念图象的分析,把握两者的关系,如图1所示。
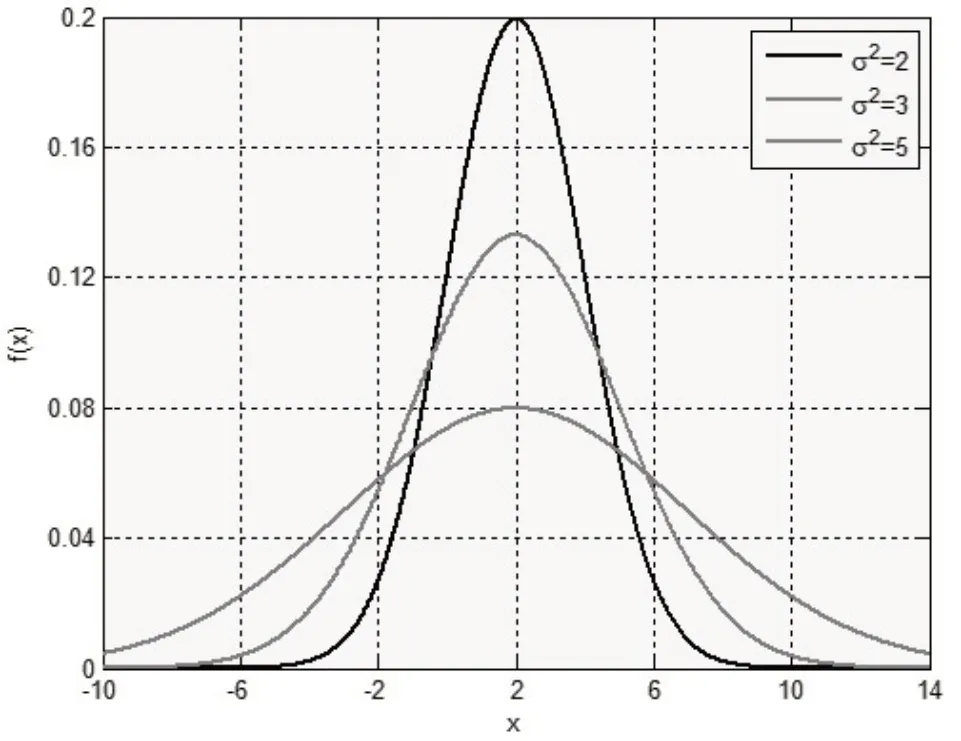
图1 正态分布的概率密度函数
2 知识思想的一体化
数据分析作为统计的核心,由于现实问题中所涉及的样本数据量较大,且在借助其不同的数字特征进行总体特征估计时由于运算量大,学生课堂可操作性不足。这使得知识零碎、公式繁密、计算复杂且结果含义深奥成为学生概率统计学习的重要痛点。学生在概率统计学习时也常常表现出只见“公式”而忽视其背后“统计思想、概率规律”等应用更为广泛的大片森林。因而,在教学时如何让学生的重心从繁杂的计算转向对概率意义以及统计思想的理解是实现深度学习的首要问题。而利用数学软件通过实验演示、模拟大数据内隐含的规律往往很直观。同时利用数学软件进行统计问题求解也很简洁直观,对比传统理论计算使其更加深刻地掌握统计思想方法。
例2:抽取一批某种产品并测量其寿命(千小时)数据如下:
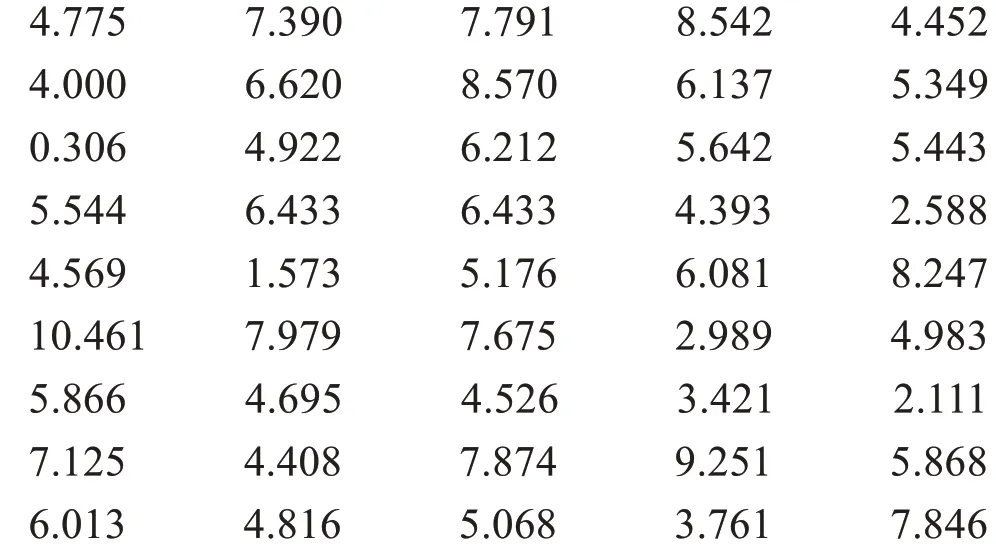
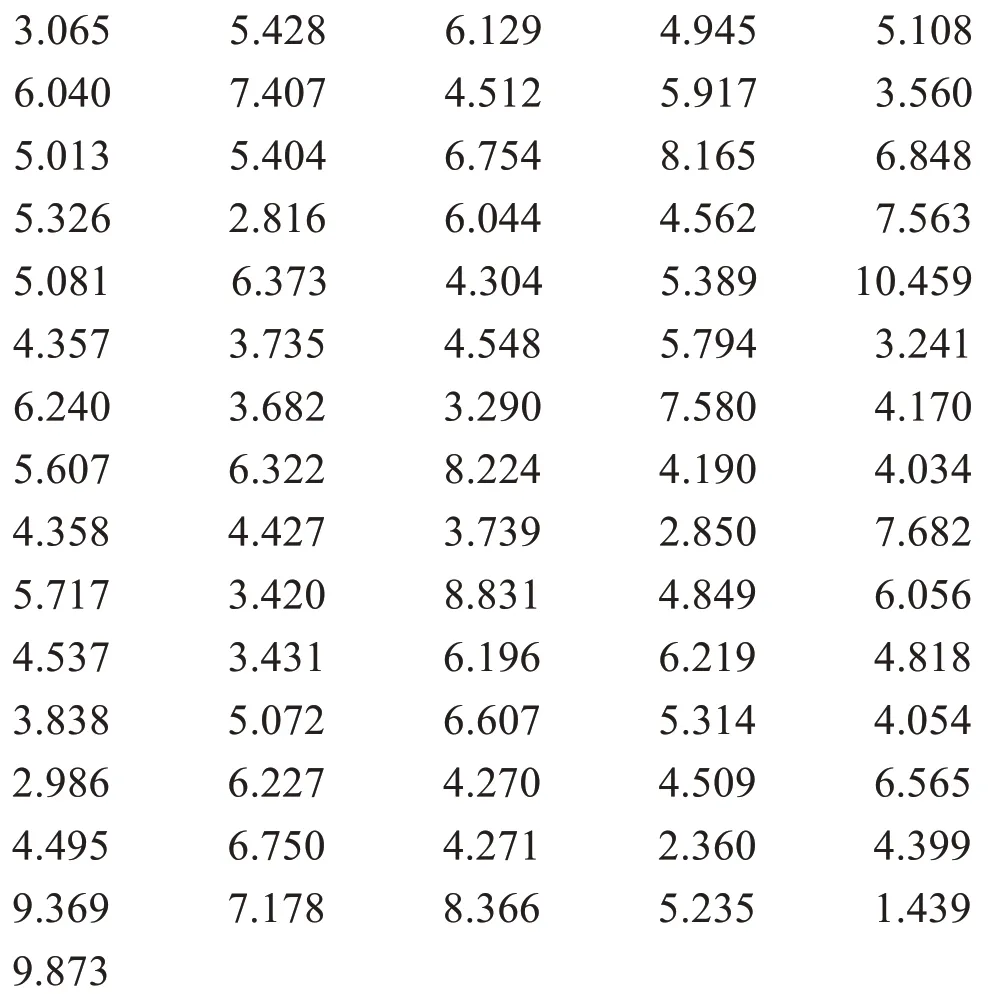
试估计该产品寿命服从的分布并验证。
实验程序:
clc;clear all;
hist(b,10)
grid on
xlabel('x', 'FontSize', 10); ylabel(' 频数', 'Font-Size',10);
normplot(b)
首先是作频数直方图,如图2所示。
其次是分布的正态性检验,如图3所示。

图3 正态性检验图
MALAB 软件作为“矩阵实验室”,其中包含了大量的数值计算、数据分析与绘图功能。因而,在教学中可以通过设计大样本数据计算验证统计规律的问题,引发学生结合理论方法的思考,感知实操性的不足。同时围绕实际案例在理论方法学习的基础上借助MALAB软件的计算功能对数据处理过程进行简化,引导学生在观察、分析相关图像特征与计算结果中体会其中所蕴含的概率规律、统计思想及其实际应用,引导学生深层次把握知识本质的同时实现知识、技能、思想、方法的一体化认识。
例3:甲乙两个车间生产的同一种零件的尺寸(cm)数据如下,零件的尺寸都服从正态分布,总体方差反应出各车间生产零件的精度,请用假设检验的方法比较两个车间的精度有无差别。
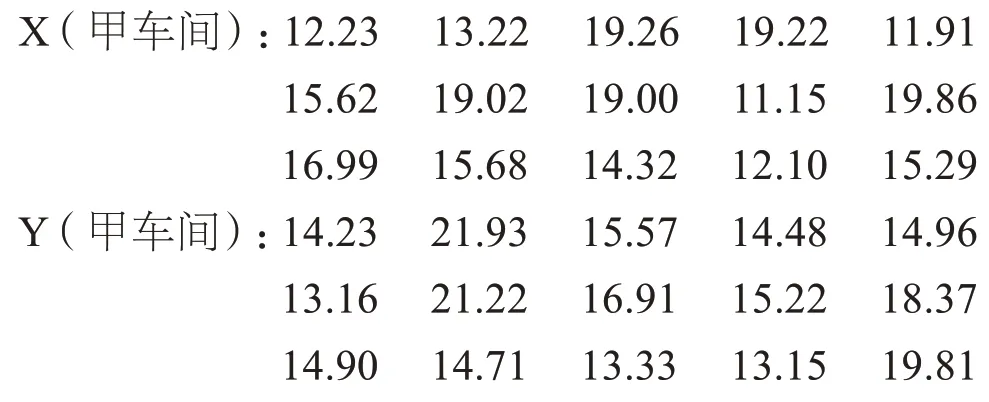
由上面分析可得样本观测值没有在拒绝域,即在显著性水平α= 0.05 的情况下认为两个车间的加工的零件精度无显著性差异。
软件验证:clc; clear all;

alpha=0.05;%设置显著性水平为0.05
tail='both';%设置尾部类型为双侧
[h,p,varci,stats]=vartest2(x,y,alpha,tail)%vartest2
函数为两个正态总体的方差比检验,varci为返回置信区间。
以上两种解法返回相同的结果,通过软件求解加深理论知识理解,同时掌握理论在现实有效的应用。
借助大样本数据的实际案例引导学生分步骤对其进行探索。首先,通过引导学生运用所学理论方法对其产品寿命的分布计算步骤思路进行表述与交流;其次,当学生感知其实操性的繁复与困难时及时启发他们寻找更为有效的工具——MALAB软件,结合学生所讨论的思路方法运用软件对其分布进行实现与验证。在此问题的解决过程中不仅有助于学生对所学知识的巩固与应用,并在观察分布特征中加深对随机现象的理解,而且能自觉感知信息技术是知识学习及解决问题的有效工具。
3 实际问题的综合化
统计推断作为统计建模的基本手法与思想,是统计思维的重要元素。在实际问题解决中,常常需要做多项统计推断的工作。在教学此类综合例题课题时若对所涉及的分项统计问题依次进行讲解举例,不仅不能很好地体现课题的整体性,且零散的方法介绍也不利于学生的理解掌握。因而,可以引入MTLAB 软件开展统计综合实验,引导学生小组合作将所学的概率论、统计学甚至其他学科知识进行有机结合,通过对其思路、方法的交流借助MTLAB 软件进行统计综合求解,并对结果进行分析讨论。学生在经历问题分析、软件操作以及结果分享过程中不仅能培养主动应用统计知识观察、分析、解决实际问题的能力,也积累了统计建模、数据分析等实践经验,能促使课堂教学从理论走向实践。
例4:为了研究早中晚时间段阅读效率的差异,连续两周统计了某一位阅读者十分钟中的阅读字数(个)情况如下。
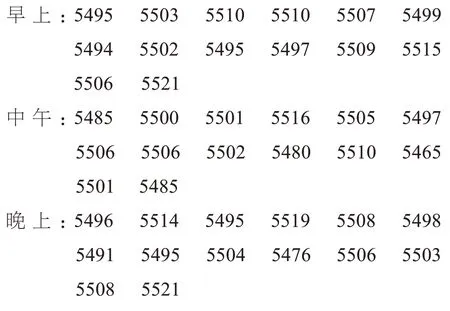
请估计阅读者阅读字数的均值并做正态性检验及方差分析。
首先,借助MATLAB 软件mle 函数做极大似然估计得3个总体的均值估计值分别约为5505,5497,5502,如图4所示。
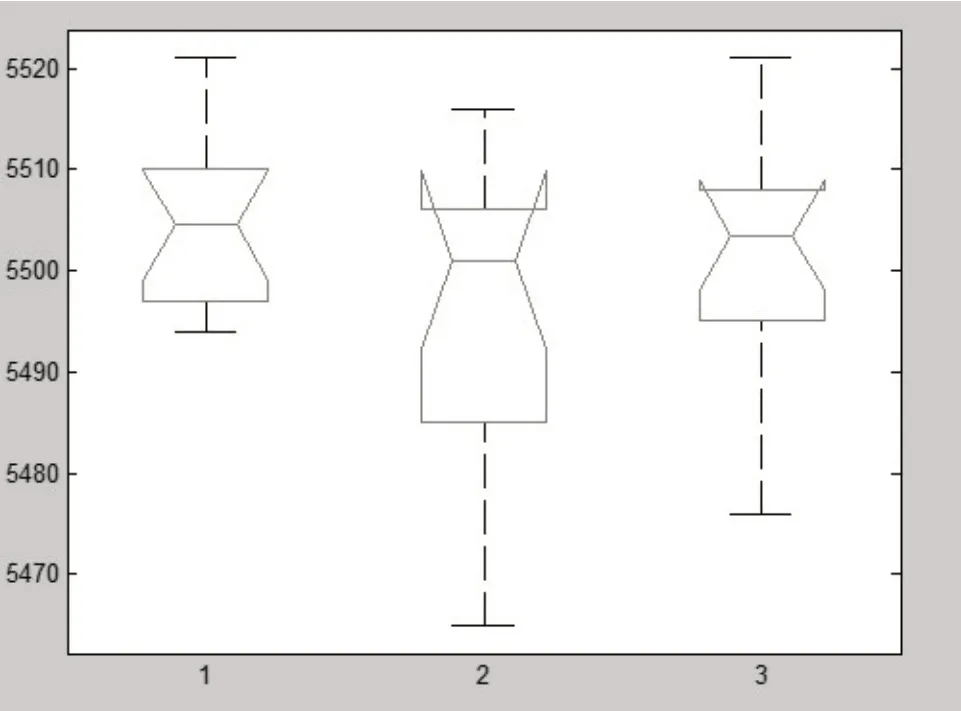
图4 方差分析显著性箱线图
其次,利用函数lillietest验证3 个总体都服从正态分布。
最后,利用MATLAB 软件中anova1 函数做方差分析。从图5中可以看出,在显著性水平α= 0.05的情况下这个阅读者早中晚阅读水平无显著性差异。
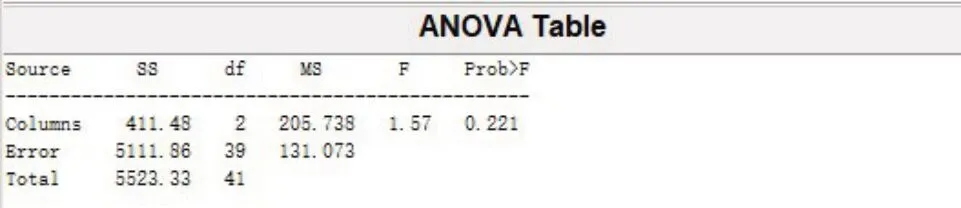
图5 方差分析ANOVA图
基于学生学习中的实际问题出发,引导学生小组运用统计的视角对其进行探究。基于不同小组学生对思路方法的分享比较,促使学生自我感知分项理论方法的繁复性。基于学生的认知冲突适时引导学生借助MATLAB软件函数库开展综合实验,并通过对两种方法思路以及过程的比较,促使学生感知软件操作以及结果直观显示所具有的优越性,体会概率统计知识的应用价值以及与现实生活的联系。
4 总 结
利用Matlab 软件进行概率统计课程实验化创新教学,不仅能将抽象的知识可视化,还可以把概率理论、统计方法与软件应用进行有机融合,让繁复枯燥的概率统计课堂教学变得生动有趣,复杂抽象的统计综合问题变得简单明了。为了促进学生统计思维能更好形成,在教学时可以鼓励学生运用统计的视角、思维与语言来观察、思考现实生活,发现和提出相关的概率统计问题,并借助所学知识以及MATLAB 等数学软件对其进行分析、求解与讨论,在知识迁移中体会概率统计的思想方法,获得数学软件的应用实践能力。
