SPCA和OCHD相结合的旋转机械早期微弱故障检测方法

李鑫 程军圣 吴小伟 王健 杨宇

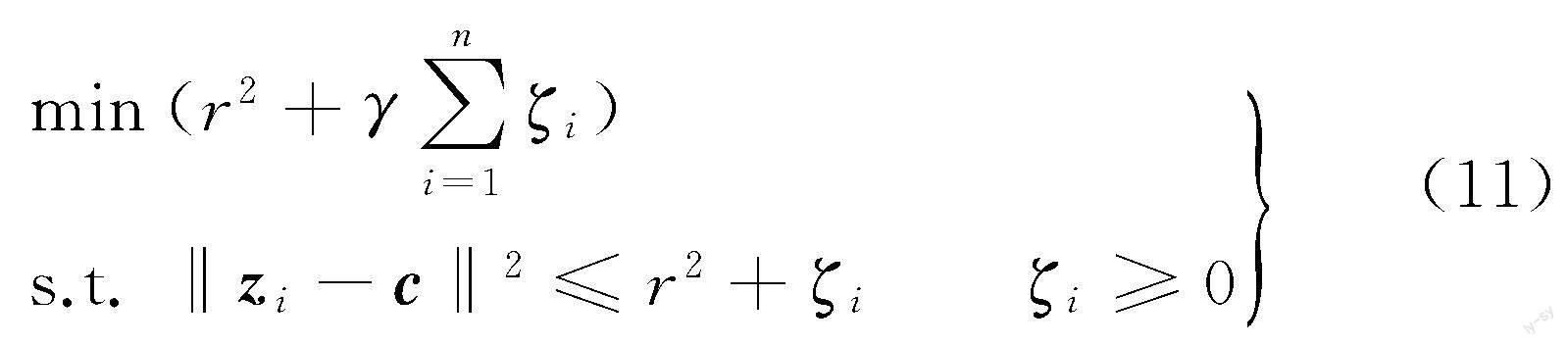
摘要：针对旋转机械早期微弱故障难以被及时准确检测的问题，提出了一种基于辛主成分分析（SPCA）和单分类超圆盘（OCHD）的智能检测方法。首先，采用SPCA将振动信号映射到辛空间，并提取最能表征信号主要能量和有效信息的辛特征值作为旋转机械故障特征。然后，将超圆盘模型引入单分类领域，提出了OCHD模型，该模型采用超圆盘模型评估已知样本的类别分布，并通过寻找几何模型上距离原点最近的点来构建最优单分类超平面，从而实现早期微弱故障的智能检测。最后，采用辛辛那提大学轴承全寿命周期数据验证所提方法的有效性，实验结果表明：SPCA能够有效提取轴承的敏感故障信息，且OCHD的故障检测性能明显优于其他单分类模型。

关键词：微弱故障检测；旋转机械；辛主成分分析；超圆盘模型；单分类超圆盘

中图分类号：TH17

DOI：10.3969/j.issn.1004-132X.2023.15.005

Early Weak Fault Detection Method of Gear Rotating Machinery by

Combining SPCA and OCHD

LI Xin1，2 CHENG Junsheng1，2 WU Xiaowei3，4 WANG Jian4 YANG Yu1，2

1.State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body，Hunan University，

Changsha，410082

2.Hunan Provincial Key Laboratory of Equipment Service Quality Assurance，Hunan University，

Changsha，410082

3.AECC Hunan Aviation Powerplant Research Institute，Zhuzhou，Hunan，412002

4.AECC Key Laboratory of Aero-engine Vibration Technology，Zhuzhou，Hunan，412002

Abstract： Aiming at the problems that early weak faults of rotating machinery were difficult to detect in time and accurately， an intelligent detection method was proposed based on SPCA and OCHD. Firstly， SPCA was used to map vibration signals to a symplectic space， and the symplectic eigenvalues which might best characterize the main energy and effective information of the signals were extracted as the fault features of rotating machinery. Then， the hyperdisk model was introduced into the one-class classification domain to propose the OCHD model. OCHD used the hyperdisk model to evaluate the class distribution of known samples， and the optimal one-class hyperplane was constructed by finding the closest points on the geometric model to the origin， so as to realize the intelligent detection of early weak faults. Finally， the effectiveness of the proposed method was verified by the bearing life cycle data from the university of Cincinnati. The experimental results show that SPCA may effectively extract the sensitive fault information of bearings， and the fault detection performance of OCHD is significantly better than that of other one-class models.

Key words： weak fault detection； rotating machinery； symplectic principal component analysis（SPCA）； hyperdisk model； one-class hyperdisk（OCHD）

0 引言

對于旋转机械，设备失效一般是由微弱故障逐渐演化而来的［1］，因此，开展旋转机械的早期微弱故障检测研究对保障设备长期安全稳定运行、避免严重的生产事故和人员损失具有十分重要的意义［2］。然而，旋转机械振动信号通常是由多源复杂信号与噪声信号耦合而成的，具有非线性（各源信号非线性叠加）、非平稳的特点，这就造成早期微弱故障信息极易被其他干扰成分所淹没［3］，因此，如何及时准确地检测出设备的早期故障仍是一个具有挑战性的难题。

智能故障检测的核心步骤包括故障特征表征和检测模型的构建［4］。故障特征表征是通过信号分析方法提取能够反映旋转机械故障状态的敏感特征。目前，绝大多数故障特征表征方法都是从欧氏几何角度对信号进行分析处理的。近年来，以辛几何为基础的时序信号分析方法为该领域的研究提供了一条有效的途径。例如，LEI等［5］将辛几何与信息熵相结合，提出了基于辛熵的轴承故障特征提取方法，该方法能有效提取轴承的本质故障特征。CHENG等［6］提出了基于辛变化熵的齿轮早期故障特征提取方法，实验结果验证了该方法的有效性。PAN等［7］提出了辛几何模态分解（symplectic geometry mode decomposition，SGMD）方法，以保持原始数据的本质特征不变，并增强旋转机械故障信息。郑直等［8］通过SGMD方法对原始信号进行重构，并提取重构信号中的时域、频域统计参数作为故障特征，作为核模糊C均值聚类模型的输入，以实现轴承的智能故障诊断。LI等［9］提出了一种辛稀疏支持矩阵机模型，并将其应用于轴承故障诊断，该模型能够自动在辛空间中提取轴承的有效故障成分，并实现轴承状态的自动判别。此外，LEI等［10］将辛几何整合到主成分分析（principal component analysis，PCA）方法中，提出了基于辛主成分分析（symplectic principal component analysis，SPCA）的时间序列分析方法。不同于传统的PCA方法，SPCA将数据映射到辛空间，采用辛相似变换保持数据的本质特征不变，并挖掘数据的主要特征，消除数据的冗余特征及噪声成分。鉴于SPCA优异的特征提取性能，本文采用SPCA对振动信号进行预处理，以提取旋转机械的本质故障信息。在SPCA中，辛特征值（symplectic eigenvalue，SE）反映了原始数据在辛空间不同方向上的能量分布，故选取最能表征信号主要能量和有效信息的辛特征值作为旋转机械故障特征。

旋转机械绝大多数时间都运行在正常状态下，这就造成了正常状态数据丰富，而故障状态数据获取困难，极端情况下甚至无法获得任何故障数据，因此，旋转机械故障检测实质上是一个单分类问题。目前在故障检测领域常采用的单分类模型有单分类支持向量机（one-class support vector machine，OCSVM）［11］、支持向量数据描述（support vector data description，SVDD）［12］、单类凸包分类（one-class classification based on convex hull，OCCCH）［13］等。FERNNDEZ-FRANCOS等［14］通过提取振动信号边频带特征构建OCSVM，实现了轴承微弱故障的智能检测。SAARI等［15］着重研究了OCSVM的结构参数对轴承故障检测精度的影响，同时给出了参数设置的指导方案。SHIN等［16］将SVDD应用于复杂机电设备的故障检测，并取得良好的故障检测效果。WANG等［17］提取频谱度量指标与多尺度散度熵作为敏感故障特征，并采用SVDD实现机械设备早期故障的在线检测。ZENG等［18］提出了基于OCCCH的轴承故障检测方法，实验结果验证了该方法的有效性。NEZ等［19］构造了一种混合近似OCCCH模型，用于工业生产的异常值检测。从计算几何的角度分析，SVDD和OCCCH都采用一个几何模型评估已知单类样本分布，并利用未知样本与所构建幾何模型的相似性测度，判定样本是否属于异类，这启发我们探索利用其他几何模型以获得更准确地样本分布。本文将超圆盘模型引入单分类领域，提出了一种单分类超圆盘（one-class hyperdisk，OCHD）模型。该模型采用超圆盘模型评估已知样本的类别分布，并通过寻找几何模型上距离原点最近的点，构建最优单分类超平面。

本文提出了基于SPCA和OCHD的旋转机械微弱故障检测方法。首先将振动信号映射到辛空间中，采用SPCA获取数据的辛特征值。然后选取能量占比较大的辛特征值构成特征向量，并将其作为OCHD的输入。最后，根据模型的输出结果实现故障的智能检测。

1 辛主成分分析SPCA

SPCA将辛几何的概念融入传统的PCA，其核心思想是将待研究的复杂系统映射到辛空间中，并挖掘蕴藏在数据中的主要特征。在辛空间中，数据间的相互作用主要集中在前几个主要成分中，而剩余成分为冗余特征或噪声成分。与欧氏几何不同，辛几何是一种具有非线性辛结构的偶数维几何，能够充分反映复杂系统的动态信息。

给定一维时间序列x={x（1），x（2），…，x（l）}，其中l为时间序列的长度。根据Taken嵌入理论，可通过相空间重构将时间序列x重构为多维轨迹矩阵X：

其中，k为嵌入维度，τ为延迟时间，m=l－（k－1）τ。本文同样采用改进伪近邻点［20］方法和互信息函数［21］自适应地确定最优的k和τ。轨迹矩阵X中包含丰富的系统动态信息，SPCA采用辛相似变换以保持系统动态结构不变，并在辛空间中更好地刻画系统的几何信息。传统PCA主要采用SVD寻找系统中的主要成分，而SPCA是利用辛相似变换挖掘数据的主要特征。

首先，将轨迹矩阵X映射到辛空间，并构造其Hamilton矩阵：

其中，A=XTX为X的自相关矩阵。然后采用辛相似变化获取Hamilton矩阵U的特征值，具体过程如下：

（1）令V=U2，即

（2）构造一辛矩阵G，使其满足

其中，B为上Hessenberg矩阵，其元素bij=0（i>j+1）。当G为辛Household矩阵P时，由于V为实对称矩阵，矩阵V等价于矩阵U，故式（4）可改写为

式中，Q为稀疏载荷矩阵。

（3）利用辛QR算法获取矩阵B的特征值λ（B）={λ1，λ2…，λk}。值得注意的是，由于V为实对称矩阵，故A和B的特征值相等，即

（4）将特征值λ={λ1，λ2…，λk}按从大到小排序：

λ1>λ2>…λj≥λj+1≥…≥λk（7）

其中，λ为矩阵A的辛特征值，反映了系统在辛空间中不同方向上的能量分布，且能量主要集中在前j个方向上，而λi（i=j+1，j+2，…，k）代表数据中的噪声水平。本文选取能量占比为90%的前j个辛特征值作为旋转机械的敏感故障特征：

2 单分类超圆盘

在单分类问题中，通常将已知的某一类样本称为负类样本，其他未知类别样本称为正类样本。单分类超圆盘OCHD采用超圆盘模型评估已知负类样本的类别分布，并将原点视为正类样本，寻找一分类超平面f（z）=〈w，z〉－b，以分离超圆盘模型和原点。从几何的角度來看，OCHD的分类超平面f（z）由超圆盘上距离原点最近点决定：f（z）通过该最近点，并垂直于最近点与原点的连线。图1详细描绘了OCHD的分类原理。对于待测样本z～，若f（z～）≥0，说明该样本位于超圆盘一侧，为负类样本；若f（z～）<0，说明z～位于原点一侧，为正类样本。

假设有已知样本集Z={zi}ni=1，其中zi∈Rd，n为样本的个数。该样本集的超圆盘模型可表示为

其中，r、c分别表示超圆盘模型的半径和中心；βi为第i个样本的组合系数。OCHD的核心是确定超圆盘模型上距离原点最近点，因此，其目标函数可表示成以下最小模问题：

在求解式（10）之前，需先求解r和c：

其中，γ为平衡参数，用于控制模型复杂度。式（11）的拉格朗日函数可表示成

其中，θi、αi为拉格朗日乘子。分别对r、c和ζi求偏导：

则式（12）可简化为

式（14）是一个典型的QP问题，本文采用标准的QP求解方法获得其最优解θ1，θ2，…，θ*n，则超圆盘模型的中心c和半径r可表示为

将式（15）代入OCHD模型的目标函数，即式（10），并将其展开可得

式（16）是一个标准的QCQP问题，本文采用MOSEK求解器获取其最优解β*1，β*2，…，β*n，则OCHD分类超平面的法向量w和偏置b可表示为

OCHD同样可使用核技巧，即采用核函数将低维特征映射到高维Hilbert空间，以提高模型的非线性处理能力。由于高斯核函数k（zi，zj）=〈φ（zi），φ（zj）〉具有良好的泛化性和普适性，故本文采用该核函数代替向量内积〈zi，zj〉：

k（zi，zj）=exp（－‖zi－zj‖/（2δ2））（18）

式中，δ为高斯核参数。

3 基于SPCA和OCHD的故障检测流程

本文提出了一种基于SPCA和OCHD的旋转机械微弱故障检测方法，SPCA用于提取振动信号的辛特征值，作为机械故障的敏感特征，OCHD用于智能检测设备是否发生故障。所提智能故障检测方法的流程图见图2，其核心步骤如下：

（1）采集旋转机械从正常运行到最终失效的全寿命样本数据，选取部分正常运行状态的样本用于训练，剩余样本用于测试。

（2）对于每一个样本，采用SPCA将其映射到辛空间，并提取能量占比超过90%的辛特征值构成机械故障的特征向量。

（3）计算每一个辛特征值的均值和方差，并将特征归一化。

（4）采用训练样本构建OCHD模型，并获得OCHD的分类超平面。

（5）利用剩余样本测试OCHD模型，并对实验结果分析处理，以验证所提故障检测方法的有效性。

4 实验验证

4.1 数据集介绍

采用滚动轴承全寿命周期数据对所提智能故障检测方法进行实验验证，数据集来源于辛辛那提大学智能维护系统（intelligent maintenance systems，IMS）中心［22］，实验装置如图3所示。实验过程中，轴承1～4均为Rexnord ZA-2115型双列轴承，轴承的具体参数见表1。在每个轴承基座上设置一个PCB 353B33型加速度传感器，以采集系统运行过程中的振动信号。轴承所在轴的转速稳定在2000 r/min，并通过弹簧装置向转轴施加26.66 kN的径向载荷。采用NI DAQ Card 6062E型采集装置拾取该实验装置的振动信号，采样频率为20 kHz，采样间隔为10 min，每次采集的数据长度为20480个振动点。轴承全寿命周期实验用时164 h，共产生982组数据（排除最后两组失真数据）。实验后期，轴承1外圈出现明显故障，因此本文采用轴承1上的振动信号进行实验分析。基于表1，可以计算得到轴承内圈、滚动体、外圈和保持架的故障特征频率分别为296.9 Hz、139.9 Hz、236.4 Hz和14.8 Hz。各故障特征频率的计算公式详见文献［22］。

首先，采用SPCA算法对轴承全寿命周期数据进行分析，获取能量占比超过90%的辛特征值作为轴承故障的敏感特征。实验结果表明，每组振动数据的前15个辛特征值的能量占比均超过90%，因此本文选取每组数据的前15个辛特征值作为特征向量，最终形成大小为982×15的全寿命周期特征矩阵，特征选择结果如图4所示。

然后，将全寿命周期的前100组数据视为轴承正常运行的数据，采用前100组数据训练OCHD模型，并使用剩余的数据验证模型的故障检测性能。在OCHD模型的构建过程中，利用5折交叉验证方法确定其最优结构参数，即平衡参数和高斯核参数。此外，为了验证所提OCHD模型的优越性，引入SVDD、OCSVM、OCCCH三个经典的单分类模型进行对比分析。为了保证对比结果的公平性，各对比模型的最优参数也同样采用5折交叉验证方法确定。对于OCHD、OCSVM和OCCCH模型，直接将－f（z）作为轴承状态的评价指标；而对于SVDD模型，取样本到超球体模型中心的广义距离作为评价指标。因此，各模型的故障报警阈值都统一设置为零。当一个样本的评价指标为正数时，该样本将判定为故障样本。

各模型的故障检测结果如图5所示。由图5a可以看出，OCHD模型的评价指标在第533组样本之前都低于故障报警阈值，而从第533组样本开始，

评价指标超过故障报警阈值，并且报警一直持续到轴承寿命加速实验结束。

同理，由图5b～图5d可知，SVDD、OCSVM和OCCCH模型也是从第533组数据开始，评价指标持续超过报警阈值。为了验证轴承是否是从第533组数据开始出现故障，对第532组、533组、550组和600组数据进行包络谱分析，分析结果如图6所示。

图6a中没有明显的轴承故障特征频率，说明此时轴承正常运行。由图6b可以看出，第533组数据的包络谱在230.7 Hz处有明显的谱峰，且该频率与轴承外圈故障特征频率极其相近，因此可以断定此时轴承出现了微弱的外圈故障。此外，由图6c和图6d可以看出，第550组和第600组数据的包络谱中出现了明显的近似故障特征频率及其倍频，且随着轴承寿命加速实验的继续，特征频率及其倍频的幅值也越来越大，这说明轴承状态在持续恶化。

综上，轴承在533组数据之前都运行状态良好，但从第533组数据开始出现了外圈故障。基于此结论，再次观察图5可知，SVDD、OCSVM和OCCCH模型在第533组数据之前都产生了不同程度的误报警，而所提OCHD模型无任何误报警，因此其检测精度达到100%。与之相应，SVDD、OCSVM和OCCCH的检测精度分别为98.75%、98.64%和98.98%。实验结果表明，所提OCHD模型能够准确检测轴承微弱故障，且相较于其他单分类模型，其故障检测性能更为优异。此外，所有模型都采用辛特征值作为轴承敏感故障特征，并且检测精度都超过98.5%，这也从侧面反映了辛特征值能够准确表征轴承性能退化状态。

为了研究所提模型在噪声环境下的鲁棒性，分别在原始振动信号中添加-2～2 dB的高斯白噪声，不同噪声程度下各模型的故障检测结果见表2。可以看出，OCHD模型在每种噪声程度下都取得了最高的故障检测精度，甚至在强背景噪声（-2 dB）下，其检测精度仍达92.75%，这进一步证明所提方法能够有效检测旋转机械早期微弱故障。

为了验证各模型在较少训练样本下的故障检测性能，分别选用前20、40、60和80组数据训练各单分类模型，并使用剩余数据测试模型性能。不同训练样本下OCHD模型的故障检测结果见图7。可以看出，随着训练样本的增加，所提OCHD模型的诊断性能逐渐提高，直到训练样本为80时，故障检测精度达到100%。另外，不同训练样本下各模型的故障检测精度见表3。

由表3可以看出，所提OCHD模型在每种训练样本情况下都取得了最高的故障检测精度。在训练样本个数仅为20时，OCHD模型的检测精度为97.40%，明显高于其他单分类模型。此外，

当训练样本个数超过40时，OCHD模型的检测精度稳定在99%以上，这也再次验证了该模型在小样本情况下具有良好的故障检测性能。

4 结论

（1）SPCA在辛空间对振动信号进行分析处理，能够保持原始数据的结构信息，消除冗余特征和噪声成分，因此，所提取的辛特征值能够准确表征轴承性能退化状态。

（2）相较于其他单分类模型，所提OCHD模型采用超圆盘模型估计已知样本的类别分布，提供了更合适的样本边界，因而在理论上具有更优异的单分类性能。实验结果表明，OCHD具有更高的故障检测精度，且在小样本情况下，该模型的性能优势更加明显。

参考文献：

［1］ 杨路航，李宝庆，王平，等.基于概率输出弹性凸包的滚动轴承故障诊断方法［J］.中国机械工程，2021，32（1）：40-46.

YANG Luhang， LI Baoqing， WANG Ping， et al. Fault Diagnosis Method of Rolling Bearings Based on Probability Output Flexible Convex Hull［J］. China Mechanical Engineering， 2021，32（1）：40-46.

［2］ 余浩帥， 汤宝平， 张楷， 等.小样本下混合自注意力原型网络的风电齿轮箱故障诊断方法［J］.中国机械工程， 2021， 32（20）：2475-2481.

YU Haoshuai， TANG Baoping， ZHANG Kai， et al. Fault Diagnosis Method of Wind Turbine Gearboxes Mixed with Attention Prototype Networks under Small Samples［J］. China Mechanical Engineering， 2021，32（20）：2475-2481.

［3］ QIAO Z， LEI Y， LI N. Applications of Stochastic Resonance to Machinery Fault Detection：a Review and Tutorial［J］. Mechanical Systems and Signal Processing， 2019， 122：502-536.

［4］ 赵志宏， 李乐豪， 杨绍普， 等. 一种无监督的轴承健康指标及早期故障检测方法［J］. 中国机械工程， 2022， 33（10）：1234-1243.

ZHAO Zhihong， LI Lehao， YANG Shaopu， et al. An Unsupervised Bearing Health Indicator and Early Fault Detection Method［J］. China Mechanical Engineering， 2022， 33（10）：1234-1243.

［5］ LEI M， MENG G， DONG G. Fault Detection for Vibration Signals on Rolling Bearings Based on the Symplectic Entropy Method［J］. Entropy， 2017， 19（11）：607.

［6］ CHENG J， YANG Y， LI X， et al. An Early Fault Diagnosis Method of Gear Based on Improved Symplectic Geometry Mode Decomposition［J］. Measurement， 2020， 151：107140.

［7］ PAN H， YANG Y， LI X， et al. Symplectic Geometry Mode Decomposition and Its Application to Rotating Machinery Compound Fault Diagnosis［J］. Mechanical Systems and Signal Processing， 2019， 114：189-211.

［8］ 郑直，高崇一，宋金超，等.基于SGMD敏感参数和KFCMC的滚动轴承故障诊断方法［J］.机床与液壓，2020，48（11）：189-193.

ZHENG Zhi， GAO Chongyi， SONG Jinchao， et al. Fault Diagnosis Method of Rolling Bearings Based on SGMD Sensitive Parameters and KFCMC［J］. Machine Tool ＆ Hydraulics，2020，48（11）：189-193.

［9］ LI X， YANG Y， SHAO H， et al. Symplectic Weighted Sparse Support Matrix Machine for Gear Fault Diagnosis［J］. Measurement， 2021， 168：108392.

［10］ LEI M， MENG G. Symplectic Principal Component Analysis：a New Method for Time Series Analysis［J］. Mathematical Problems in Engineering， 2011， 2011：793429.

［11］ HEJAZI M， SINGH Y P. One-class Support Vector Machines Approach to Anomaly Detection［J］. Applied Artificial Intelligence， 2013， 27（5）：351-366.

［12］ ZHANG F， FAN H， WANG R， et al. Deep Dual Support Vector Data Description for Anomaly Detection on Attributed Networks［J］. International Journal of Intelligent Systems， 2022， 37（2）：1509-1528.

［13］ FERNNDEZ-FRANCOS D， FONTENLA-ROMERO， ALONSO-BETANZOS A. One-class Convex Hull-based Algorithm for Classification in Distributed Environments［J］. IEEE Transactions on Systems， Man， and Cybernetics：Systems， 2017， 50（2）：386-396.

［14］ FERNNDEZ-FRANCOS D， MARTNEZ-REGO D， FONTENLA-ROMERO O， et al. Automatic Bearing Fault Diagnosis Based on One-class ν-SVM［J］. Computers & Industrial Engineering， 2013， 64（1）：357-365.

［15］ SAARI J， STRMBERGSSON D， LUNDBERG J， et al. Detection and Identification of Windmill Bearing Faults Using a One-class Support Vector Machine （SVM）［J］. Measurement， 2019， 137：287-301.

［16］ SHIN H J， EOM D H， KIM S S. One-class Support Vector Machines—an Application in Machine Fault Detection and Classification［J］. Computers & Industrial Engineering， 2005， 48（2）：395-408.

［17］ WANG Q， LIU X， WEI B， et al. Online Incipient Fault Detection Method Based on Improved 1 Trend Filtering and Support Vector Data Description［J］. IEEE Access， 2021， 9：30043-30059.

［18］ ZENG M， YANG Y， LUO S， et al. One-class Classification Based on the Convex Hull for Bearing Fault Detection［J］. Mechanical Systems and Signal Processing， 2016， 81：274-293.

［19］ NEZ I， JOVE E， CASTELEIRO-ROCA J L， et al. Hybrid Approximate Convex Hull One-class Classifier for an Industrial Plant［C］∥Computational Intelligence in Security for Information Systems Conference. Cham， 2019：282-292.

［20］ YI J， WU L， ZHOU W， et al. ASparse Dimensionality Reduction Approach Based on False Nearest Neighbors for Nonlinear Fault Detection［J］. IEEE Transactions on Systems， Man， and Cybernetics：Systems， 2019， 51（8）：4980-4992.

［21］ SONG X， ZHANG Y， GONG D， et al. FeatureSelection Using Bare-bones Particle Swarm Optimization with Mutual Information［J］. Pattern Recognition， 2021， 112：107804.

［22］ INCE T， MALIK J， DEVECIOGLU O C， et al. EarlyBearing Fault Diagnosis of Rotating Machinery by 1d Self-organized Operational Neural Networks［J］. IEEE Access， 2021， 9：139260-139270.