基于磨削热变形分析的切入式外圆磨削去除率的修正模型与实验研究

迟玉伦 武子轩

摘要：为解决切入式外圆磨削加工中磨削热变形引起的传统磨削去除率模型与实际磨削偏差较大的问题，基于磨削热变形机理分析，对传统切入式外圆磨削去除率模型进行了修正。通过分析切入式外圆磨削过程中砂轮与工件的磨削热变形量及热变形速率，确定了修正函数，建立了基于磨削热变形的切入式外圆磨削材料去除率修正模型，并通过磨削实验对模型进行了验证。结果表明，修正模型具有更高的准确性。

关键词：切入式外圆磨削；热变形；材料去除率；实验研究

中图分类号：TH161

DOI：10.3969/j.issn.1004-132X.2023.15.002

Correction Model and Experimental Study of Removal Rate in Tangential Cylindrical Grinding Based on Grinding Thermal Deformation Analysis

CHI Yulun WU Zixuan

School of Mechanical Engineering，University of Shanghai for Science and Technology，Shanghai，200093

Abstract： In order to solve the problem in plunge type cylinder grinding caused by the traditional grinding removal efficiency model of grinding thermal deformation is different from the actual grinding， the traditional grinding removal efficiency model was modified based on the analysis of grinding thermal deformation mechanism. By analyzing the grinding thermal deformation and thermal deformation rate of grinding wheel and workpiece， the correction function was determined， the material removal efficiency correction model based on the thermal deformation was established. The model was verified by grinding experiment， and the results show that the model has higher accuracy.

Key words： plunge type cylindrical grinding； thermal deformation； material removal rate； experimental study

0 引言

与其他外圆磨削加工方式相比，切入式磨削加工能获得较高的表面质量［1-2］，但在加工过程中，砂轮和工件的接触弧内会产生大量磨削热，引起热变形，影响磨削材料去除过程和工件最终的表面精度［3］。近些年，随着对产品零件表面质量要求的提高，磨削热变形对工件加工质量的影响变得不可忽视［4］，因此，提高磨削材料去除率模型预测精度，对提高外圆切入式磨削加工精度、保证磨削质量具有重要的意义。

切入式磨削加工中，磨削力作为表征磨削加工情况的主要参数，与磨削热变形直接相关。CHOI等［5］基于系统分析和实验建立了用于外圆磨削工艺的通用磨削力模型，该模型结构简单并具有良好的预测能力，适用于不同条件的磨削加工，通过少量实验即可确定模型系数，但他们未详细讨论磨削力与磨削条件的关系。WANG等［6］发现磨削力的平均值随砂轮速度增大而减小，随砂轮速度、磨削深度、磨粒顶角、工件进给速度增大而增大，而上述4个参数与磨削材料去除率密切相关，因此将磨削力作为影响材料去除率的主要因素。MARSH等［7］提出一种基于监测磨削力的磨削材料去除模型，实验结果表明该模型有较高的准确性，能在多变磨削条件下精确控制磨削工件的外圆尺寸。實际加工中，受限于机床加工条件，磨削力传感器不便安装于理想位置。姜晨等［8］针对外圆切入式磨削加工，提出了一种采用声发射信号实现轴类零件材料去除率在线监测的方法，推导了声发射信号与工件材料去除率的关系，建立了一种基于声发射信号的磨削去除率预测模型，实验证明该模型具有良好的预测精度，但声发射信号对传感器安装精度要求较高且容易受到各种因素干扰。CHI等［9］将时间常数作为模型关键参数，建立了基于功率信号的磨削材料去除率模型，研究表明磨削功率信号与磨削力具有很好的线性关系，并通过实验验证了功率信号切入式磨削去除率模型的有效性。上述磨削材料去除率模型虽然反映了磨削加工中的磨削去除率的变化，但忽视了高速磨削引起的磨削热变形，难以准确预测切入式外圆加工过程中的磨削去除率。GUPTA等［10］指出，磨削加工过程中的绝大部分能量转化为热能并传导到砂轮和工件中，引起砂轮和工件发生热变形、产生较高的热应力，利用有限元法对磨削操作产生的热应变进行分析，发现随着工件深度的增加，热应力先增大后减小。MLLER等［11］发现接触区温度取决于磨削法向力和砂轮切削速度，且随材料去除率的增大而降低，基于磨削功率建立了计算接触区温度的定量模型。HEINZEL等［12］通过分析切入式外圆磨削中的热影响及其深度效应，对磨削过程温度、接触时间和磨削功率之间的联系进行深入探究，发现受热影响的磨削深度不仅取决于磨削功率，还取决于磨削时间，且接触时间对温度梯度有很大影响。李征等［13］发现磨削温度随磨削深度的增大而升高，但温度梯度随磨削深度增大而逐步减小。上述研究结果表明热变形产生的热应力对磨削去除率产生极大影响，且温度梯度与磨削加工时间紧密相关。

基于上述分析，本文从磨削热变形的角度出发，首先对外圆切入磨削过程中砂轮和工件实际接触状态进行分析，并将砂轮和工件热变形量及热变形速率进行阶段划分，确定切入阶段和光磨阶段磨削热对磨削进给速度的影响。然后，以系统热变形速率的分段式指数方程作为修正函数，对传统的磨削材料去除率模型进行修正，建立基于磨削热变形的功率信号磨削模型（Model of Power Signal Grinding Based on Grinding Thermal Deformation），记为TPMG，并对其有效性进行验证。

1 切入式外圆磨削热变形机理分析

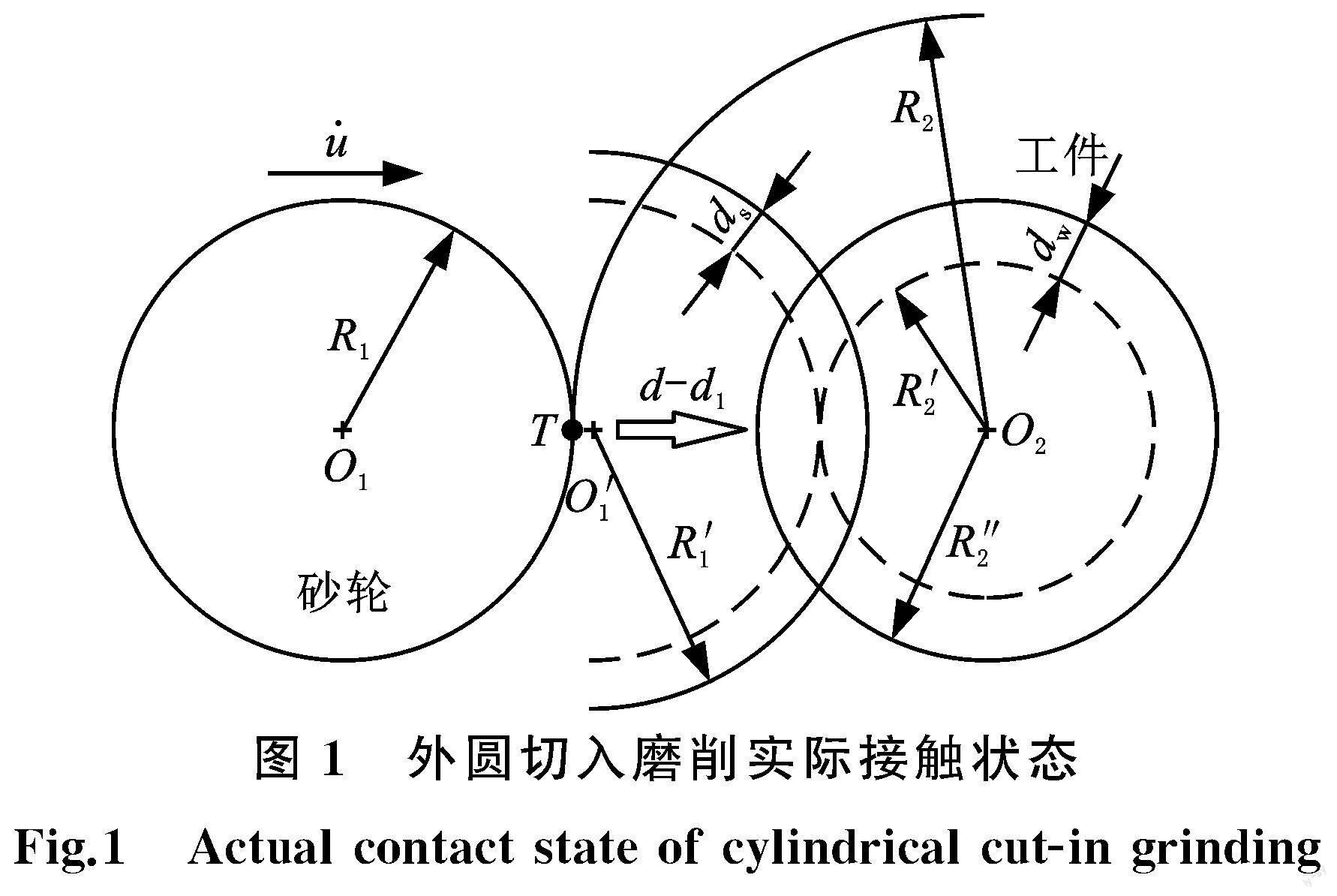
切入式外圆磨削加工过程中，砂轮磨粒切削工件表面，接触区产生的大量磨削热的绝大部分流入工件和砂轮，导致工件和砂轮发生热膨胀，使砂轮的实际切入速度加快。随着砂轮磨削深度增大，砂轮和工件的热膨胀量发生变化。为便于分析砂轮和工件在磨削过程中的热膨胀，将外圆切入磨削的实际接触状态简化。如图1所示，O1为砂轮圆心，O2为磨削工件圆心，R1为磨削开始前的砂轮半径，R2为磨削开始前的工件半径，R1′为磨削过程中砂轮发生热膨胀后的半径，R2′为未考虑热膨胀的工件半径，R2″为加入磨削热变形后的工件半径，u·为砂轮的理论进给速度。假设磨削系统的热积聚产生的热变形量只沿径向变化，砂轮和工件在T位置开始接触磨削，令砂轮架切入工件的移动量为d，系统刚度导致的磨削残留余量为d1。传统磨削理论中，砂轮切入工件表面的深度由d-d1决定。考虑热变形后，令砂轮热变形量为ds，工件热变形量为dw，则发生热膨胀后的砂轮半径R1′=R1+ds，工件半径R2″=R2′+dw，故砂轮发生热变形时的磨削深度由d-d1+ds+dw决定。

磨削过程中，砂轮和工件的热变形量随时间发生变化，如图2a所示。对热变形量求导，得到磨削系统的热变形速率，如图2b所示。

将整个磨削加工过程分为切入阶段和光磨阶段。

（1）切入阶段。砂轮以理论进给速度u·靠近磨削工件。刚进入磨削状态时的温度梯度最大，磨削系统热变形速率在短时间内达到最大值，对应图2b中的A阶段，砂轮和工件此时的热膨胀方向指向磨削区。随着磨削的持续进行，磨削系统的热变形速率从峰值开始逐渐下降，但热变形量仍在增加，对应图2中的B阶段。热变形速率减小至零后，磨削过程处于热稳定阶段，热变形速率基本不变，直至切入阶段结束。此阶段的热变形量趋于稳定，磨削系统达到热平衡状态，对应图2中的C阶段。

（2）光磨阶段。此阶段的砂轮理论进给速度为0，在磨削液作用下，磨削区温度逐渐下降，砂轮和工件的热变形量开始恢复，此时砂轮和工件处于收缩阶段，二者热收缩方向均为背离磨削区。磨削热变形作用下，砂轮的实际进给速度与理论进给速度不相等。进入光磨阶段后，砂轮和工件的热变形量及热变形速率开始呈指数下降，对应图2中的D阶段。随着弹性变形量及热变形量的减小，磨削区产生的热量及砂轮和工件中的热量持续减小直至磨削结束，对应图2的中E阶段。

基于上述分析可知，在切入阶段，由于磨削热变形的影响，砂轮在切入阶段会获得额外的加速效果；在光磨阶段，工件发生热收缩，提高了工件实际尺寸的生成速度，导致基于功率信号的磨削模型（grinding power signal model，GPSM）与实际加工情况之间出现较大偏差。根据系统热变形速度图像，将切入式外圆磨削过程中的热变形速率用分段函数表示，并作为修正函数对GPSM［14］模型进行修正。

2 基于磨削热变形的切入式外圆磨削去除率修正模型

根据对切入式外圆磨削实际接触状态和磨削热变形机理的研究，本节在传统磨削去除率模型的基础上，结合磨削热变形在磨削加工中的变化，对切入阶段和光磨阶段进行模型修正，并根据磨削功率信号建立切入式外圆磨削去除率修正模型。

2.1 磨削材料去除率模型

GPSM建立在磨削系统发生弹性变形的基础上，将整个磨削系统简化为表示砂轮和工件在磨削过程中发生的弹性变形和接触变形的3个弹簧系统，如图4所示。图4中，ks为砂轮刚度，kw为工件刚度，ka为砂轮与工件的接触刚度。该系统的等效刚度为

机床按照设定的进给速度u·运行，砂轮在磨削力的作用下磨除工件上的余量，磨削过程中产生的磨削力可以分为切向磨削力和法向磨削力［15］。法向磨削力Fn是导致工件产生弹性变形δ的主要原因，二者的关系可表示为

法向磨削力Fn的大小和磨削過程中砂轮实

式中，kc为磨削力系数；a为工件每转下的进给深度；nw为工件转速。

2.1.1 切入阶段的磨削材料去除率模型

式中，a1、b1为未知常系数。

式中，a2、b2为未知常系数。

将式（2）、式（3）代入式（6）可得

将式（4）、式（5）代入式（7）可得

求解式（8）可得A阶段磨削去除率模型：

B、C阶段的磨削去除率模型为

式中，C1为常数。

2.1.2 光磨阶段的磨削材料去除率模型

式中，a3、b3、c2为未知常系数。

式中，a4、b4、c3为未知常系数。

将式（11）、式（12）代入式（13）可得

求解式（14）可得光磨阶段材料去除率模型，其中，D阶段材料去除率模型为

E阶段材料去除率模型为

2.2 TPMG的建立与求解

P′=Ft′vs（17）

式中，vs为砂轮线的速度。

则磨削砂轮主轴的功率为

P=kpFtvs（18）

式中，kp为取决于磨削条件的功率系数；Ft为切向磨削力。

法向磨削力Fn与切向磨削力Ft的关系为［21］

Fn=kntFt（19）

式中，knt为法向磨削力与切向磨削力的比例系数。

联立式（3）、式（9）、式（16）、式（17）可得基于功率信号的切入阶段磨削材料去除率模型，其中，A阶段磨削材料去除率模型为

B、C阶段磨削材料去除率模型为

联立式（3）、式（14）、式（16）、式（17）可得基于功率信号的光磨阶段磨削材料去除率模型，其中，D阶段磨削材料去除率模型为

E阶段磨削材料去除率模型为

式（20）、式（21）有诸多未知常系数，如时间常数τ，常系数k1、k2、knt、kp、kc等。时间常数τ可根据功率信号变化率计算，为保证τ的计算准确性，选取图2b中的D阶段，使用最小二乘拟合法对时间常数进行计算求解。得到时间常数后，结合功率信号，使用最小二乘法可求得k1、k2、knt、kp、kc等常系数。磨削过程材料去除率模型的参数求解如图5所示。

3 实验设置

本次实验以切入式外圆磨削加工为研究对象，通过功率传感器测量磨削信号，利用理论模型预测功率曲线，验证改进后的磨削去除率模型的有效性和实用性。

如图6所示，本次实验使用的机床为德国斯莱福临公司STUDERKC33精密外圆磨床，头架主轴转速为120 r/min，最小进给量为0.1 μm；砂轮型号为53A80L15V，厚度为62 mm，直径为480 mm，磨削时的砂轮线速度为30 m/s；工件材料为45钢，直径为50 mm；切入阶段磨削余量设定为0.1 mm，切入进给速度设定为8μm/s。磨削冷却液为嘉实多Hysol R水基磨削液。功率传感器采用美国LOAD CONTROL公司的PH-3。功率传感器安装在机床电气柜中，实时采集磨削加工功率信号。采集卡选用美国INSTRUMENTS的 DI-2108，使用WinDaq軟件采集并保存数据。

本文利用功率传感器、USB数据采集卡和电脑等设备搭建功率信号采集系统，传感器通过BNC连接线与采集卡相连，采集卡通过USB接口连接计算机。在计算机中对WinDaq采集软件进行设置，将采集卡每个通道的采样频率设定为1 kHz，采集系统部署完毕后即可实现对工件外圆磨削过程进行连续的实时状态监测。为避免加工单一工件时出现实验数据的偶然性，采集多次磨削的数据用于理论模型研究。

实验使用TAYLOR HOBSON圆度测量仪测量工件外圆表面的圆度，如图7a所示。通过圆度测量仪配套的计算机软件记录实验数据，计算机软件采用最小二乘中心法（MZC）进行圆度评定。将工件的回转中心与精密轴系同心安装，并自动校准探针以保证测量数据的准确性，选取离工件上端面18 mm 处位置进行圆度测量，如图7b所示。

使用美国SDHY-6212B便携式非接触激光粗糙度仪测量工件的平均表面粗糙度。工件磨削加工结束后测量工件表面粗糙度，如图8所示。

4 实验分析与研究

4.1 基于GPSM的实验分析

根据第3节中的机床参数进行磨削加工实验并采集功率信号，为避免多次实验加工之间产生的磨削热量的相互影响，在单个零件磨削结束后，先将砂轮冷却至常温状态、再进行下阶段的磨削，取磨削功率信号中的单次磨削加工功率信号进行数据分析。实际磨削加工中，机床启动和砂轮空转会产生不可忽略的功率消耗，将其记为Prun和Pidle，由于TPMG从砂轮和工件进入磨削状态后开始拟合，所以模型拟合功率Pgrind为［22］

Pgrind=Ptotal-Prun-Pidle（24）

式中，Ptotal为测量功率。

测量功率信号如图9所示，其中Prun=151 W。由于砂轮与工件磨削加工开始和结束后的功率相等，因此以磨削加工结束时的功率即end point为参考点绘制end level直线，end level与测量功率曲线相交于start point，以start point为模型预测曲线的起点，对end level以上功率信号进行模型拟合，此时Prun+Pidle=220 W，按照磨削加工工艺要求将测量功率信号划分为切入阶段和光磨阶段。

按照图5中的方法求解模型中的未知参数，使用最小二乘法拟合法求解功率信号较为稳定的光磨阶段时间常数τ，最终求得τ=0.457，如图10所示。

GPSM拟合所需参数u·（t）、nw、vs在第3节已给出。将最小二乘拟合法求出的时间常数τ代入GPSM中，绘制磨削材料去除率功率预测曲线。由图11可以看出，GPSM虽然在一定程度上能反映砂轮磨削加工过程中的功率变化，但未考虑热变形对磨削材料去除率的影响，导致切入阶段中的预测曲线与测量曲线存在较大偏差（图11中的M区）。在光磨阶段，GPSM预测曲线虽然和实际测量功率曲线的起点、终点相同，但与测量曲线之间存在较大偏差（图11中的N区）。

综上所述，GPSM的预测结果与实际功率有较大差异，不能很好地反映磨削过程中功率的变化，为准确描述实际磨削过程中磨削去除率的变化过程，分析磨削热变形对材料去除率的影响，使用TPMG重新进行功率预测。

4.2 基于TPMG的实验分析

根据磨削热变形机理分析可知，在切入阶段，系统热变形速率经历了三个阶段：热变形速率上升阶段（A部分）、热变形速率下降阶段（B部分）、热变形速率保持不变阶段（C部分）。光磨阶段经历了两个阶段：热变形速率下降阶段（D部分）、缓慢上升阶段（E部分）。通过插值拟合法将功率散点信号拟合成功率曲线，再对拟合曲线进行求导，结果如图12所示。对比图2与图12可以看出，实际磨削速率的变化趋势与系统热变形速率的变化趋势一致，在切入阶段均表现为急剧增大至峰值后缓慢减小，在光磨阶段表现为磨削速率急剧减小后缓慢恢复。所以，以切入阶段磨削速率峰值为分割点F，以光磨阶段速率峰值为分割点H，G点设定在功率信号初次达到功率最大值位置。

圖13中，S点为磨削起始点，P点为结束点，J点为切入阶段结束点，将F、G、H点对应至实际功率图像中。以F点为分割点，将切入阶段分为SF段和FJ段，使用式（18）对SJ段进行模型预测。以H点为分割点，将光磨阶段分为JH段和HP段，使用式（19）对JP段进行模型预测。

4.2.1 TPMG切入阶段分析

以F点为分界点，当砂轮和工件进入磨削状态后，在磨削热变形的影响下，砂轮和工件处于磨削不稳定状态，功率信号波动幅度（功率信号波峰与波谷的差值，见图13）Δkw开始增大，到达F点时的功率信号波动幅度达到最大值Δkw，max。随着磨削进给深度增大，磨削区温度达到最大且逐渐保持在这一稳定状态，砂轮热变形量也逐渐稳定，功率信号波动幅度Δkw逐渐减小至最小值，系统进入稳定状态。

使用式（18）对SF段进行功率预测，预测曲线如图14所示，使用式（18）对FJ段进行功率预测，预测曲线如图15所示。从图14、图15中可以看出，TPMG预测曲线与实际测量功率曲线在切入阶段的重合度更高，消除了GPSM在切入阶段出现的预测偏差。将GPSM与实际功率曲线之间的偏差值定义为dk，从图14中可以看出，GPSM预测曲线从S点开始逐渐偏离实际功率曲线，dk逐渐增大，dk在F点时达到最大值，记为dkmax。将TPMG与实际功率曲线之间的偏差值定义为dv，偏差值在F点处最大，记为dvmax，如图15所示。GPSM与TPMG在切入阶段的整体对比如图16所示。

图17所示为GPSM与TPMG预测曲线在切入阶段与实际功率曲线之间的偏离情况。由图17可以看出，dvmax远小于dkmax，且TPMG的平均偏差均小于GPSM的平均偏差，证明了TPMG的有效性。

为建立dvmax和表面加工质量的关系，在切入阶段结束后测量工件的圆度测量和粗糙度，测得圆度为5.54 μm、表面粗糙度为0.885 μm，通过计算机记录的工件外圆轮廓如图18a所示，工件表面粗糙度如图18b所示。

4.2.2 TPMG光磨阶段分析

光磨阶段以H点为分界点，使用式（19）对光磨阶段进行磨削材料去除率的预测，JH段、HP段的的功率预测曲线分别如图19、图20所示。由图19可以看出，GPSM和TPMG在光磨阶段初期的拟合效果较好，但随着加工时间的延长，TPMG出现偏差最大值dvmax′。接近H点时，dk开始增大，直至偏差最大值dkmax′，如图20所示。

GPSM与TPMG在光磨阶段的对比如图21所示。相较于GPSM，TPMG与实际测量功率曲线的重合度更高。

针对光磨阶段GPSM和TPMG的预测曲线与实际功率曲线之间偏离情况进行分析。由图22可以看出，TPMG预测曲线与实际功率曲线之间的偏差较小，进一步体现了TPMG的有效性。

为建立dvmax和加工质量的关系，在光磨阶段结束后测量工件的圆度和粗糙度，测得圆度为0.71 μm、表面粗糙度为0.185 μm，通过计算机记录的工件外圆轮廓如图23a所示，工件表面粗糙度如图23b所示。

4.2.3 TPMG磨削全过程分析

TPMG在单次磨削加工中的预测曲线如图24所示，可以看出TPMG能准确跟随start point到end point之间的功率变化，并可通过模型与实际功率信号之间的差值建立模型偏差与工件加工表面质量的量化关系，如图25所示，可以发现dvmax与工件圆度误差和表面粗糙度测量值的变化趋势一致。

为进一步探究dvmax大小与工件表面质量的关系，进行多次磨削加工实验以获得dvmax，同时记录磨削结束后工件圆度和表面粗糙度，建立dvmax与表面质量的关系图（图26）。

可以看出，dvmax与工件加工表面质量呈负相关，实际功率与模型的偏差越小，工件表面质量（粗糙度和圆度）越高。后续可通过dvmax在线监测评估工件磨削加工表面的质量，为外圆切入磨削工艺在线优化提供解决方案。

5 结论

（1）根据对切入式外圆磨削实际接触状态和磨削热变形机理的研究，在传统磨削去除率模型的基础上，结合切入阶段和光磨阶段下的系统热变形速率的变化，将系统热变形速率的分段式指数方程作为修正函数，修正切入阶段和光磨阶段的磨削去除率模型，并根据磨削功率信号建立TPMG。

（2）TPMG与GPSM的实验对比分析结果表明：相较于GPSM，TPMG与实际功率曲线的偏差更小，预测精度更高。实验验证了模型偏差与工件表面质量之间的关系：功率信号与模型偏差越小，工件表面质量（粗糙度和圆度）越高。

参考文献：

［1］ 迟玉伦， 李郝林. 基于时间常数外圆切入磨削砂轮钝化的监测方法［J］. 中国机械工程， 2016， 27（2）：209-214.

CHI Yulun， LI Haolin. Monitoring Method of Grinding Wheel Passivation Based on Time Constant Cylindrical Cutting［J］. China Mechanical Engineering， 2016， 27（2）：209-214.

［2］ 朱峰， 曹硕生， 雷力生. 外圆切入磨削加工精度的研究［J］. 机械工程学报， 1993， 29（5）：104-109.

ZHU Feng， CAO Shuosheng， LEI Lisheng. Study on Machining Accuracy of Cylindrical Plunge Grinding［J］. Chinese Journal of Mechanical Engineering， 1993， 29（5）：104-109.

［3］ DING Zishan， JIANG Xiaohui， GUO Miaoxiao， et al. Investigation of the Grinding Temperature and Energy Partition during Cylindrical Grinding［J］. The International Journal of Advanced Manufacturing Technology， 2018， 97：1767-1778.

［4］ ZHAO A Z， QIAN N. Prole Grinding of DZ125 Nickel-based Superalloy：Grinding Heat， Temperature Field， and Surface Quality［J］. Journal of Manufacturing Processes， 2020， 57：10-22.

［5］ CHOI T J， SUBRAHMANYA N， LI H， et al. Comprehensive Analysis of the Thermal Impact and Its Depth Effect in Grinding［J］. CIRP Annals—Manufacturing Technology， 2008， 48（1）：61-72.

［6］ WANG C， CHEN J. Study on Brittle Material Removal in the Grinding Process Utilizing Theoretical Analysis and Numerical Simulation［J］. The International Journal of Advanced Manufacturing Technology， 2016， 87：2603-2614.

［7］ MARSHE R， MOERLEIN A W， DEAKYNE T R S， et al. In-process Measurement of Form Error and Force in Cylindrical-plunge Grinding［J］. Precision Engineering， 2008， 32（4）：348-352.

［8］ 姜晨， 李郝林， 麦云飞. 基于声发射信号的外圆切入磨削去除率监测［J］. 中国机械工程， 2013， 24（22）：2992-2996.

JIANG Chen， LI Haolin， MAI Yunfei. Monitoring the Removal Rate of Cylindrical Plunge Grinding Based on Acoustic Emission Signal［J］. China Mechanical Engineering， 2013， 24（22）：2992-2996.

［9］ CHI Y， GU J， LI H. Optimization of Internal Plunge Grinding Using Collaboration of the Air-grinding and the Material Removal Model Based on the Power Signal［J］. The International Journal of Advanced Manufacturing Technology， 2019， 105：247-264.

［10］ GUPTA R， SEKHON G. Stress due to a Moving Band Source of Heat and Mechanical Load on the Work Surface during Grinding［J］. Journal of Materials Processing Technology， 1997， 70：274-278.

［11］ MLLERU， PRINZ S. Analysis of the Thermo-mechanical Load and Productivity during Force-compliant Grinding of pcBN［J］. Journal of Materials Processing Technology， 2022， 305：117604.

［12］ HEINZEL C， HEINZEL J. Comprehensive Analysis of the Thermal Impact and Its Depth Effect in Grinding［J］. CIRP Annals—Manufacturing Technology， 2021， 70：289-292.

［13］ 李征， 丁文鋒， 周欢. 基于混合材料模型的颗粒增强钛基复材高速磨削温度研究［J］. 机械工程学报， 2019， 55（21）：186-198.

LI Zheng， DING Wenfeng， ZHOU Huan， et al. Study on High Speed Grinding Temperature of Particle Reinforced Titanium Matrix Composites Based on Mixed Material Model［J］. Journal of Mechanical Engineering， 2019， 55（21）：186-198.

［14］ CHI Yulun， LI Haolin， CHEN Xun. In-process Monitoring and Analysis of Bearing Outer Race Way Grinding Based on the Power Signal［J］. Proceedings of the Institution of Mechanical Engineers， 2017， 231（14）：2622-2635.

［15］ MAHATA S， SHAKYA P， BABU N R， et al. In-process Characterization of Surface Finish in Cylindrical Grinding Process Using Vibration and Power Signals［J］. Procedia CIRP， 2020， 88：335-340.

［16］ MARSH E R， MOERLEIN A W， DEAKYNE T R S， et al. In-process Measurement of Form Error and Force in Cylindrical-plunge Grinding［J］. Precis Eng. ， 2008， 32（4）：348-352.

［17］ JAMSHIDI H， BUDAK E. Grinding Temperature Modeling Based on a Time Dependent Heat Source［J］. Procedia CIRP， 2018， 77：299-302.

［18］ CHEN X， ROWE W B， MILLS B， et al. Analysis and Simulation of the Grinding Process. Part Ⅲ. Comparison with Experiment［J］. International Journal of Machine Tools and Manufacture， 1996， 36（8）：897-906.

［19］ HECKERR L， LIANG S Y， XIAO Jianwu， et al. Grinding Force and Power Modeling Based on Chip Thickness Anlaysis［J］. Int. J. Adv. Manuf. Technol. ， 2007， 33（5/6）：449-459.

［20］ TAWAKOLI T. Developments in Grinding Process Monitoring and Evaluation of Results［J］. Int. J. Mechatronics and Manufacturing Systems， 2008， 4（1）：307-320.

［21］ SUN L， YANG S. A New Model of Grinding Forces Prediction for Machining Brittle and Hard Materials［J］. Procedia CIRP， 2015， 27：192-197.

［22］ 遲玉伦. 基于功率信号的切入式磨削工艺优化关键技术研究［D］. 上海：上海理工大学， 2016.

CHI Yulun. Research onKey Technology of Cutting-in Grinding Process Optimization Based on Power Signal［D］. Shanghai：University of Shanghai for Science and Technology， 2016.