基于推力分配的自主水下机器人推进器容错控制研究

孙啸天，曾庆军，尚 乐，刘子豪，戴晓强

（江苏科技大学 自动化学院，江苏 镇江 212000）

0 引言

自主水下机器人（Autonomous Underwater Vehicle，AUV）被广泛应用于复杂的海洋环境中，执行油气开发、设备维护、地形考察等任务［1］。21 世纪以来，世界各国在海洋资源开发的竞争中愈发激烈，加强自主水下机器人的研究与开发因此具有重要的战略意义。

在AUV 运动控制中，执行器扮演着至关重要的角色，主要包括推进器与舵。由于舵在方向控制上存在滞后性，因此使用侧推代替舵来控制艏向，随着搭载推进器数量增多，发生故障的概率随之增加，例如推进器缠绕、变形、破损、卡住等故障。因此，对发生故障的推进器进行有效的容错控制是保证AUV 稳定运行的必要条件。

近年来，AUV 推进器容错控制的研究越来越深入［2］，容错控制方法可分为被动容错控制与主动容错控制［3，4］。被动容错控制主要采用闭环控制系统应对一些特定故障［5］；主动容错控制则是在故障发生后基于故障信息有针对性的调节控制器参数，达到容错控制效果［6］。

目前，自主水下机器人容错控制的研究大多采用主动容错控制方法。Wang 等［7］将容错控制与动态控制器设计解耦，在控制分配过程中以分配误差最小和控制成本最低为优化目标，采用非线性规划解决容错控制问题，既保证了推力最大化，又实现了航行最优效率。褚振忠等［8］使用神经网络进行故障诊断，提出一种包含饱和因子的神经网络权值调整法，在实现自主水下机器人容错控制的同时，提升了推力分配的精度与稳定性。Guo 等［9］使用滑模容错控制器，根据推进器故障调整控制器的输出，实现快速有效的容错控制，但AUV 属于大惯性系统，在目标轨迹突变时会出现推进器推力饱和的现象，尤其在推进器发生部分故障导致推力不足时更为严重。

为此，本文引入权值矩阵，通过调节故障系数以达到重构推力模型的目的，有效避免了因推力饱和而导致系统失控的情况。针对AUV 作业过程中推进器存在的故障，建立自主水下机器人空间六自由度矢量模型，设计反步滑模运动控制器实现了运动控制与跟踪功能。仿真结果表明，该方法能使AUV 的实际运动轨迹趋于期望轨迹，高效地实现了AUV 的精准运动跟踪，当推进器出现故障时可在短时间内补偿AUV 故障造成的推力损失，使AUV 回到期望路径上继续进行水下作业任务。

1 研究对象描述

1.1 推进器

本文选用自主研发的“探海I 型”自主水下机器人，如图1 所示。该AUV 搭载5 路推进器，其中1 号推进器为主推，2、3 号推进器为前后侧推，4、5 号推进器为前后垂推，推进器分布如图2所示［10］。

Fig.1 AUV physical object图1 AUV实物

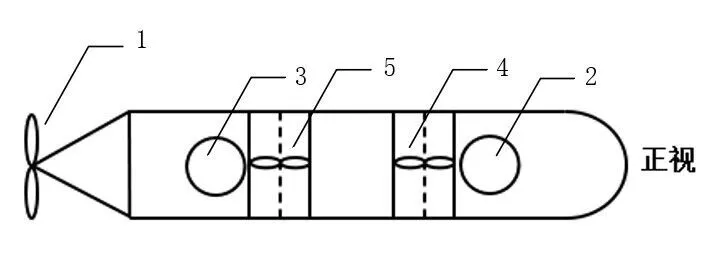
Fig.2 AUV thruster distribution图2 AUV推进器分布

由于自主水下机器人搭载的推进器在安装时左右对称，因此推进器不具备控制横摇的力矩。两路垂推控制垂向、纵倾运动；两路侧推控制横向、摇艏运动；主推控制纵向运动。本文假设推进器模型是线性的，推进器推力可表示为：

式中：D为螺旋桨直径；n为螺旋桨转速；t为推力减额系数（可忽略不计）；KT为无因次推力系数。

设侧推力矩为d1，垂推力矩为d2，推进器各推力数据为T1、T2、T3、T4、T5，前进推力、横移推力、俯仰推力、水平力矩、垂直力矩分别如式（2）—式（6）所示。

1.2 自主水下机器人动力学模型

为了便于描述自主水下机器人的动力学模型，通常会建立大地坐标系E-ξηζ和运动坐标系O-xyz，如图3所示。

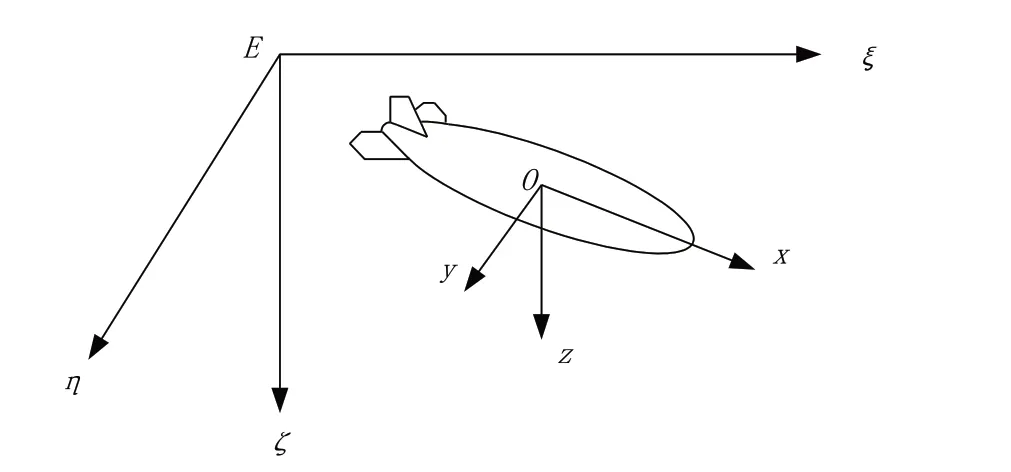
Fig.3 AUV motion and geodetic coordinate system图3 AUV运动与大地坐标系

假设AUV 为对称的刚体，质量为常数。在惯性坐标系下建立六自由度空间动力学模型为：

式中：v=[uvwpqr]T为定义在运动坐标系中的速度与角速度向量，分量分别对应纵向速度、横向速度、浮沉速度、横滚角速度、纵倾角速度与航向角速度；η=[xyzφθφ]T为定义在惯性坐标系中的位置与姿态向量，姿态分量分别对应横倾角、纵倾角及航向角；J(η)为坐标转换矩阵；M为包含附加质量的惯性力矩阵；C(v)为向心力及科氏力矩阵；D(v)为水动力阻尼力矩阵；g(η)为恢复力和力矩向量；τ为作用在机器人本体上6 个自由度的控制力与力矩，也称为控制输入［11］。

将AUV 的浮心作为动坐标系原点，经过长期理论研究与工程实践得到以下方程：

式中：m为AUV 的质量；xG、yG、zG为AUV 重心的坐标；Ix、Iy、Iz为AUV 在3个坐标轴上的转动惯量。

1.3 垂直面模型

本文忽略AUV 六自由度模型中的水平面分量，对其进一步简化得Z 轴方向浮潜方程（yg=0）、Y 轴方向纵倾（=0），如式（9）、式（10）所示。

式中：Fi为高斯白噪声；均为水动力参数；为多元矩阵函数G中相应分量的一阶偏导数；为多元矩阵函数G中的二阶混合偏导数；Zg、Mg为重力；Zprop、Mprop分别为z轴的推力与y轴的力矩。

1.4 水平面模型

假设AUV 深度不发生变化，只改变航向与航迹，在w=0、p=0、q=0 的条件下，AUV 水平面运动学方程可进行简化，X轴方向进退（yg=0）、Y轴方向平移（yg=0）、Z轴方向转艏（yg=0），如式（11）—式（13）所示。

2 运动控制器设计

2.1 反步滑模运动控制器

向AUV 下达运动控制指令后，要求AUV 跟踪期望姿态ηd，但由于系统运作于水下时，面临着外部未知干扰等不确定因素，将增加自主水下机器人姿态控制系统的复杂性。因此，针对这些不确定因素，反步滑模控制器能根据控制系统误差，在线更新系统参数，以适应自身动态和外界扰动的变化［12］。

首先，定义姿态跟踪误差。

选取第一个Lyapunov 函数为：

对式（15）求导得：

将式（17）代入式（16）得：

将式（7）代入式（17）并求导得：

选取第二个Lyapunov 函数为：

对式（20）求导，并将式（18）、α代入得：

为了使V2负定，采用等数趋近律得到控制输入。

式中：Λ、K2＞0均为对角常数矩阵。

将式（22）代入式（21）得：

由式（23）可知，系统跟踪误差渐近稳定，反步法在设计控制器的同时实时更新自适应律，极大提升了系统的暂态性能，使其具有良好的无超调跟踪性能，可高效实现自主水下机器人的路径跟踪功能。

2.2 基于推力分配的容错控制

虽然通过上述步骤可获得反步滑模控制器输出控制率τ，但自主研发的“探海I型”自主水下机器人装载有五路推进器，因此需要将控制率按照一定的原则进行分配。由于该系统在艏向运动存在冗余，因此通过两路侧推同时进行控制，即本文在分配推力时优先考虑艏向角，保证自主水下机器人的航向与目标点一致；参照控制量二范数最小原则，取控制量二范数的函数作为推力分配的评价函数，即J=‖T‖2。

设自主水下机器人控制器输出的期望控制力（力矩）为τ∈Rm，自主水下机器人推进器控制量为T∈Rn，推进器分部矩阵为B∈Rm*n，则控制率为：

由于水下环境复杂，AUV 在进行水下作业时易出现推进器故障等情况，因此设计一种基于推力分配的主动容错控制器重新分配推力，以抵消推进器故障造成的影响。

设定推进器最大推力的故障系数为si，当推进器处于正常状态时si=1；当推进器出现部分故障时0 ＜si＜1；当推进器出现完全故障时si=0。

式中：Bw=W-1BT(BW-1BT)-1为推进器分部矩阵B的伪逆矩阵。

因此，故障状态下推力分配的结果为：

3 实验结果与分析

3.1 实验设置

为验证本文所提出的自主水下机器人推进器容错控制方法的有效性，使用Matlab 软件进行仿真环境下的验证，关于自主研发的“探海I 型”自主水下机器人的水动力参数如表1所示。

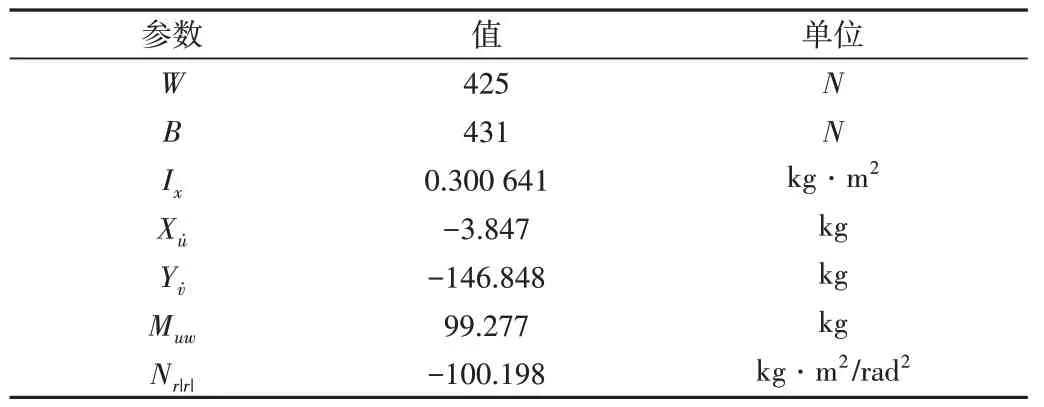
Table 1 AUV hydrodynamic parameters表1 AUV水动力参数

3.2 实验结果

仿真过程中参数设定如下：AUV 三维跟踪初始位置为（10，150，0）；水下六边形的六个目标点坐标分别为：一号点（160，90，3）、二号点（210，95，3）、三号点（240，55，3）、四号点（210，15，3）、五号点（160，10，3）、六号点（130，50，3）。图4 中；实线为推进器运行状态正常时，基于反步滑模控制的路径跟踪曲线；虚线为期望的路径跟踪曲线。由此可见，该控制器能高效实现自主水下机器人的路径跟踪功能。

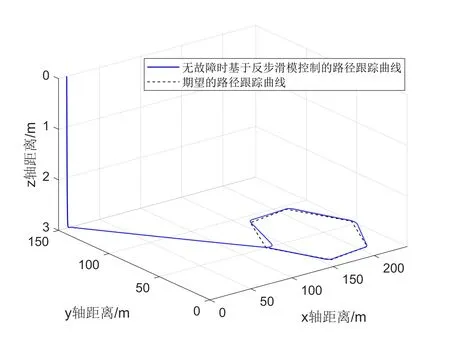
Fig.4 Hexagonal path tracking graph based on backstepping sliding mode control图4 基于反步滑模控制的水下六边形路径跟踪图

3.2.1 故障情况1

推进器初始时刻运行正常，250 s 时前侧推发生部分故障，推力减少了80%，控制器参数设定为：K1=diɑg(10，10，10)，K2=diɑg(5.5，10.5，2.5)，仿真结果如图5所示。图5 中，实线为基于推力分配的容错控制路径跟踪曲线；虚线为期望的路径跟踪曲线，*实线为无容错控制的路径跟踪曲线。表2 为发生故障情况1 后期望路径与实际路径的误差距离，采样间隔为80 s。

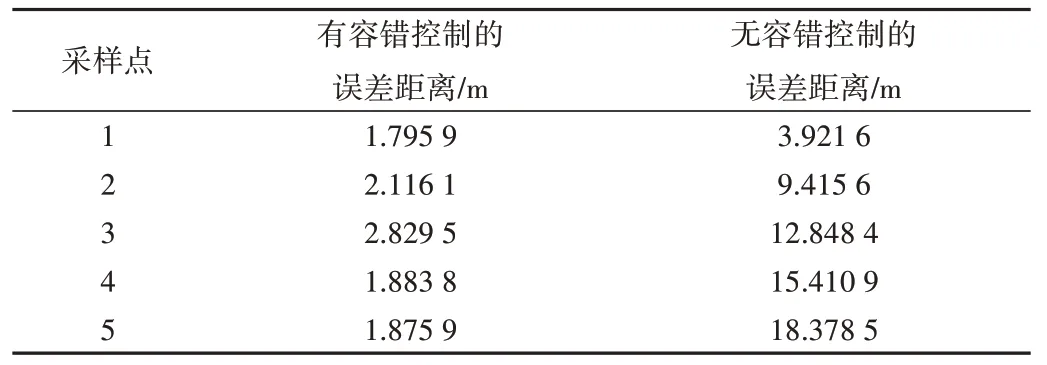
Table 2 Error distance of fault condition I表2 故障情况1误差距离

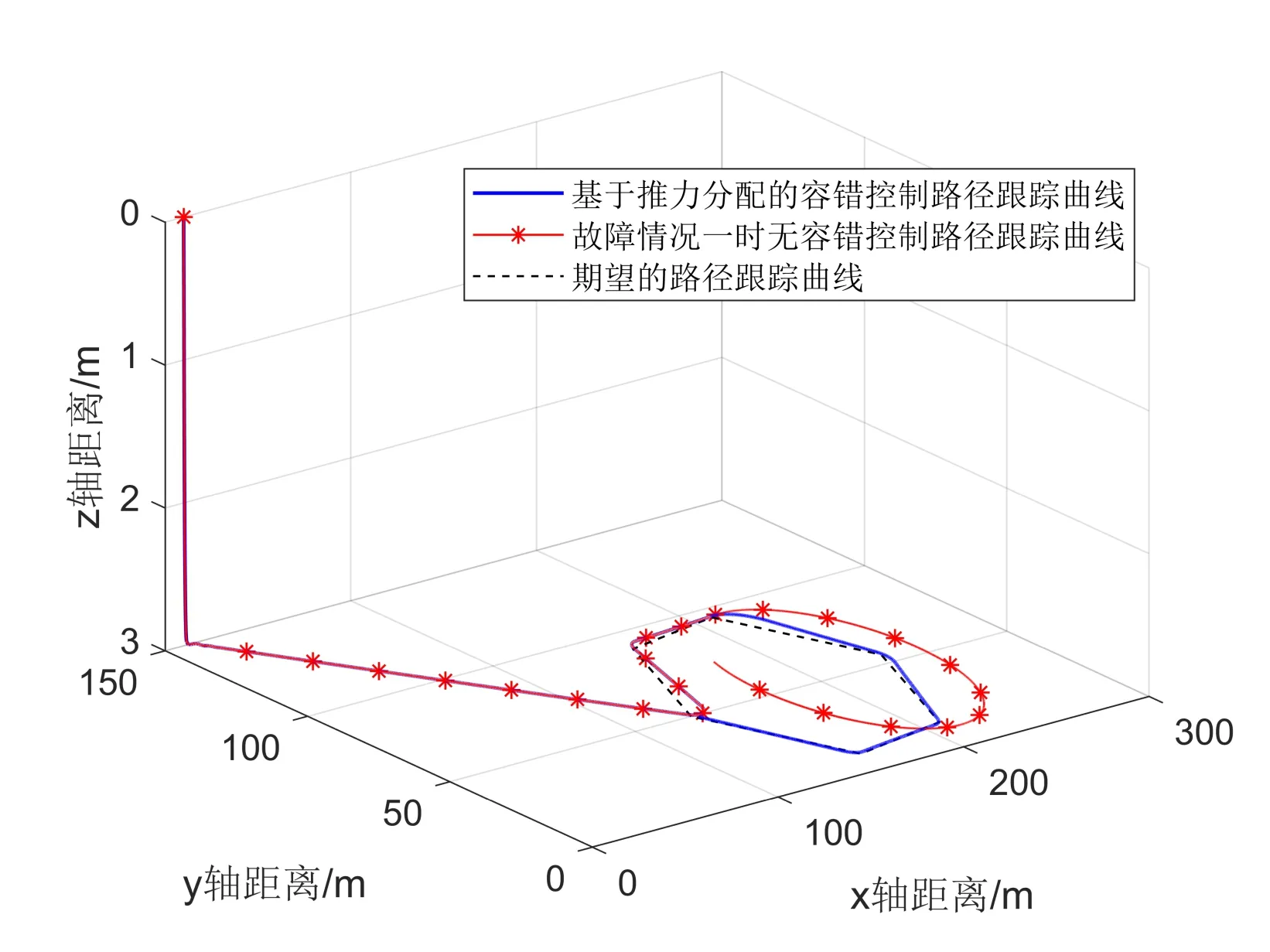
Fig.5 Curve diagram of fault condition 1图5 故障情况1曲线图

由图5、表2 可知，当AUV 发生故障后，故障轨迹的跟踪误差开始发散，无法完成预先设定好的路径跟踪任务。为此，本文采用基于推力分配的容错控制方法，当前侧推发生故障时，将故障系数设为s2=0.2，故障引起的跟踪误差逐渐收敛，最终完成预先设定好的路径跟踪任务。

3.2.1 故障情况2

推进器初始时刻运行正常，150 s 时前侧推发生部分故障，推进器推力减少30%；350 s时后侧推发生部分故障，推进器推力减少80%，仿真结果如图6所示。由此可见，当AUV 推进器发生故障时若不及时处理，将无法完成预先设定好的路径跟踪任务。

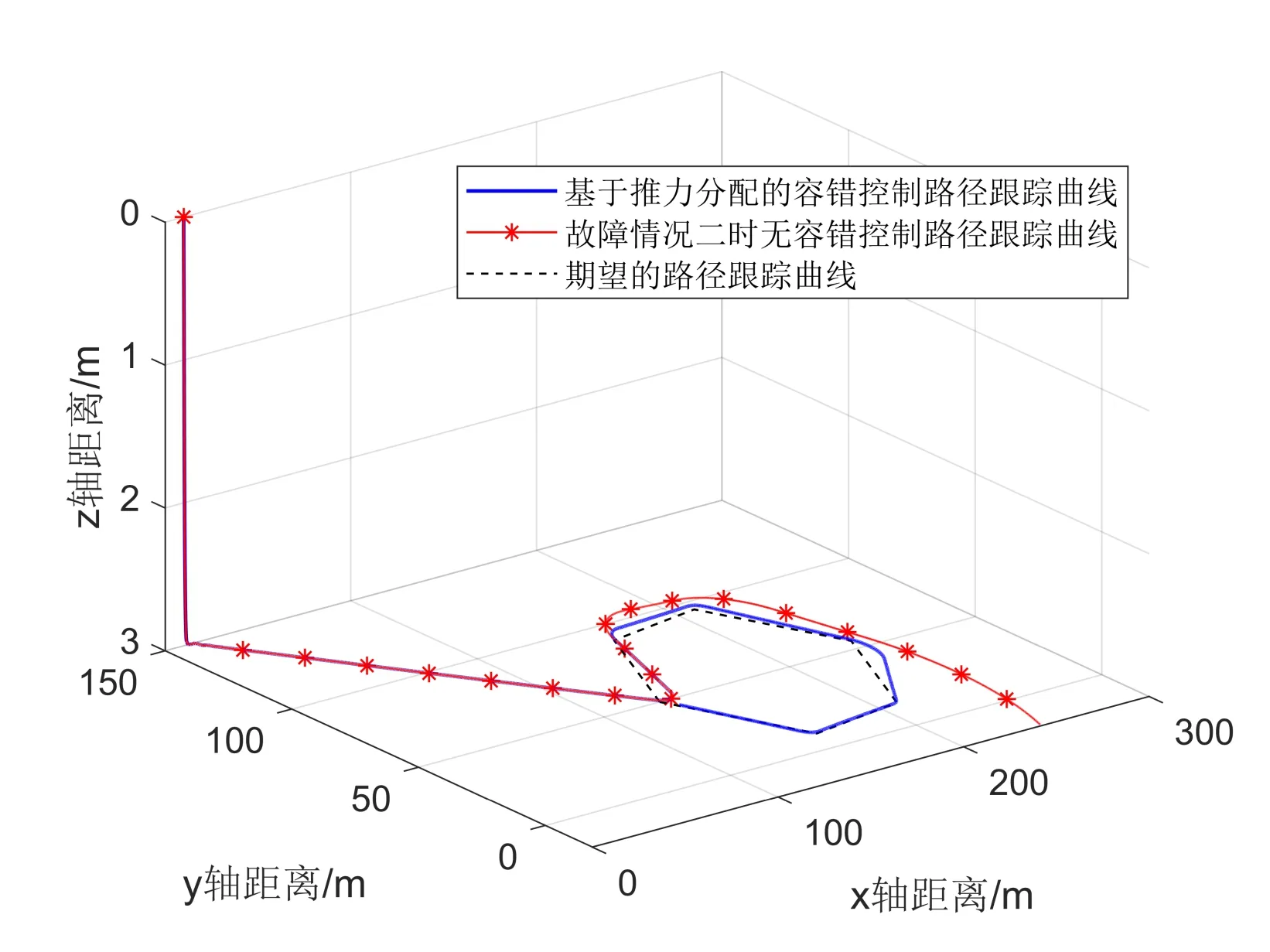
Fig.6 Curve diagram of fault condition 2图6 故障情况2曲线图

为此，本文采用基于推力分配的容错控制方法，当前侧推发生故障时，将故障系数设为s2=0.7；当后侧推发生部分故障时，将故障系数设为s3=0.2。表3 为发生故障情况2 后期望路径与实际路径的误差距离，采样间隔为80 s。由此可知，在结合容错控制方法的情况下，即使推进器发生故障，依然能保证跟踪误差收敛的稳定性，及时调整推进器输出以实现期望路径跟踪，最终完成预先设定好的任务。

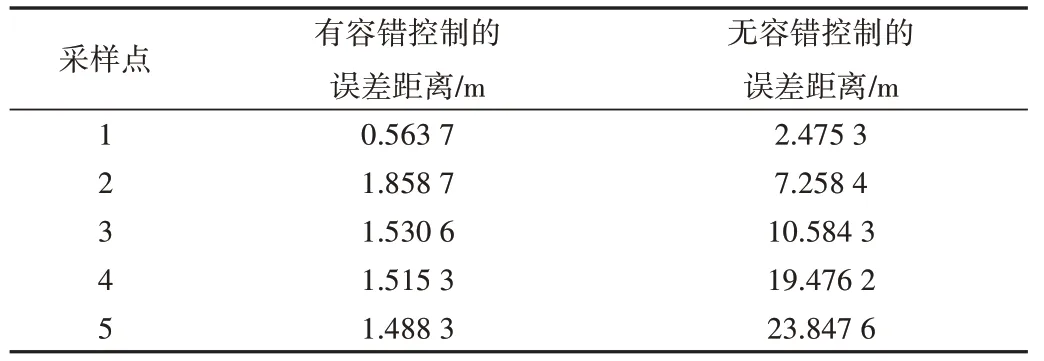
Table 3 Error distance of fault condition II表3 故障情况2误差距离

综上，仿真结果证明了基于推力分配的自主水下机器人推进器容错控制新方法的有效性。

4 结语

本文针对AUV 作业过程中存在的推进器故障问题，提出一种基于推力分配的容错控制新方法。仿真结果表明，反步滑模控制方法能使AUV 的实际运动轨迹趋于期望轨迹运行，高效地实现了AUV 的精准运动跟踪。

当推进器发生故障时，该方法能使AUV 在短时间内补偿故障造成的推力损失，使AUV 重新回到期望路径，继续进行水下作业任务。然而本文在设计水动力模型时，采用的都是符合高斯分布的白噪声，但在实际水下环境中，噪声特性极为复杂，只有进一步深入研究，才能提升AUV 在复杂水下环境的可靠性。