Numerical treatment of temporal-fractional porous medium model occurring in fractured media
2023-11-30MeherKesarwaniAvazzadeh3ONikanc4
R.Meher J.Kesarwani Z.Avazzadeh 3O.Nikan c4
a Department of Applied Mathematics & Humanities, S.V.National Institute of Technology, Surat 395007, India
b Department of Applied Mathematics, Xi’an Jiaotong-Liverpool University, Suzhou 215123, China
c School of Mathematics, Iran University of Science and Technology, Narmak, Tehran 16846-13114, Iran
Keywords:Fractured porous media Caputo fractional derivative Co-current imbibition Time-fractional partial differential equation
ABSTRACT This paper proposes a temporal-fractional porous medium model (T-FPMM) for describing the co-current and counter-current imbibition,which arises in a water-wet fractured porous media.The correlation between the co-current and counter-current imbibition for the fractures and porous matrix are examined to determine the saturation and recovery rate of the reservoir.For different fractional orders in both porous matrix and fractured porous media,the homotopy analysis technique and its stability analysis are used to explore the parametric behavior of the saturation and recovery rates.Finally,the effects of wettability and inclination on the recovery rate and saturation are studied for distinct fractional values.
1.Introduction
Fractional calculus (FC) has a significant role for studying different real-world problems arising in engineering and science.In fact,FC is an extension of integer order derivatives of arbitrary order.Later on,the theory and applications of the FC expanded greatly and numerous works [1–4] have been developed on fractional differential equations (FDEs) and integral equations.The significant role of FDEs can be found in many fields of science and engineering,such as genetic algorithms,quantum theory,damping theory,hydrocarbon reservoir problems,and Groundwater flow problems [5–13].Applications of fractional calculus can be found in a variety of areas,including transient propagation of spherical waves in porous media [14],how fluids flow in porous media [15],natural convection in slanted cavities [16],Multiphase flow in porous media using Darcy’s law and the mass conservation law [17,18],anomalous diffusion and heat transfer during thermal displacements in porous media under local thermal equilibrium [19],and wave propagation in porous media under frequency dependence [20],etc.A practical contribution of fractional calculus to the theory and model of complex fluids in real-world applications,such as fractional Langevin equation description of anomalous viscoelastic diffusion in complex fluids [21],An attenuation and dispersion model for complex viscoelastic media [22,23],Random optimal search using fractional calculus [24],Random walkers in an expanding medium using fractional diffusion equations [25],Thermal stresses in a solid with a time-varying heat source in the framework of fractional thermoelasticity [26],Nanoprecipitates form in solid solutions [27],Unsteady flow into subsurface drains [28],an analysis of non-Newtonian fluids in shear flow [29],in-homogeneous gas transport [30],Magnetic resonance imaging(MRI) diffusion models based on fractional derivatives [31,31],the prevalence of HIV/TB coinfection in multidrug-resistant TB strains[32],bone remodeling and bone tumor models using variable order derivatives [33],and many other.

Many researchers used a different approach to deal with the governing equations of such types of fractional models.Al-Smadi et al.[34] derived an explanation of the fractional heat equation based on the multistep reduced differential transform scheme.Yang et al.[35] extended the classical Homotopy perturbation method (HPM) to its fractional version for obtaining the analytical solution of the diffusion and wave equation of fractional types.Arqub and El-Ajou [36] developed a residual power series method for solving the wave and Navier-Stokes equation,space factional telegraph,and Poisson equation of time-fractional types.Aksoy et al.[37] adopted the exponential rational function scheme to derive the approximate solution of the Fokas,coupled Burgers,and Zakharov Kuznetsov Benjamin equations of space and time-fractional types.Firoozjaee et al.[38] adopted the Ritz method for time fractional Fokker-Planck equation (TFFPE).Yang and co-authors[39] applied Riesz space fractional derivative to approximate the FDE.The variational iteration method,HPM,and Adomian decomposition method were applied for solving the FDE [40–42].Using these methods,they examined the governing FDE of different realworld problems.Khan et al.[43] advanced Laplace–Adomian decomposition procedure for the fractional-order telegraph equation,while Wu [44] employed a wavelet operational scheme and found the numerical solution of the FDE.Djida et al.[45] solved the nonlocal type diffusive evolution equation with time-fractional derivative arising in a porous medium.Liao [46] introduced the Homotopy analysis method (HAM) in his doctoral work.Arqub and El-Ajou [36],Ray and Sahoo [47],Hayat et al.[48],Liao [49],Abbasbandy [50],Bataineh et al.[51],Abbasbandy [52],Bataineh et al.[53],Tan and Abbasbandy [54],Bataineh et al.[55],Kesarwani and Meher [56],Dehghan et al.[57],Ray and Sahoo [58],59 ] developed the HAM to derive the approximate solution of different versions of ordinary and partial differential equations (abbreviately,ODEs and PDEs) arising in different fields of science and engineering.They solved the various types of FDEs,namely the Burger’s and fractional Korteweg–De Vries (KdV),cubic coupled KdV,Benjamin Bona Mahony–Burger’s and Boussinesq equation,K(2,2) equation,Boussinesq–LikeB(m,n) equations,and many more such types of equations.Ray and Sahoo [47] used the modified HAM to solve the Riesz time-fractional Camassa-Holm (CH) equation in mathematical physics.
Gohil and Meher [60],Jafari and Seifi [61] implemented this method for approximating the governing fractured porous medium equation of fractional-order and diffusion-wave model.Prakasha et al.[62] conducted research on capillary gravity waves and nonlinear dispersive waves equations,namely time-fractional Kaup–Kupershmidt (KK) equations,using theq-homotopy analysis transform method (q-HATM).Mahdy [63] compared two approaches to study the solution to the TFFPE: the new iterative method (NIM)and the fractional power series method (FPSM).A time-fractional Navier–Stokes equation for the motion of flow in a pipe was modeled by Burqan et al.[64] by combining the Laplace Transform and residual power series method.Using parallel algorithms,such as the Thomas algorithm,the parallel sweep algorithm,and the accelerated over-relaxation method,Sultanov et al.[65] solved the initial-boundary problem for the time-fractional diffusion equation.Fellah et al.[14] proposed a fractional propagation equation in spherical coordinates based on a porous medium mode and obtained its solution using the Laplace transform.
The main purpose of the current work is to develop the HAM with its stability analysis to a nonlinear governing temporalfractional porous medium model (T-FPMM).It governs the cocurrent and counter-current imbibition phenomena and studies the parametric saturation and recovery rate behavior for different fractional-order in the porous and fractured matrix.
The layout of the paper is as follows.Section 2 outlines some basic definitions and properties of fractional calculus.Sections 3 and 4 discuss the extension HAM for solving a nonlinear PDE of time-fractional type and its application to the governing T-FPMM,respectively.Subsequently,Sections 6 and 5 introduce the stability analysis of the proposed method and the solution of the T-FPMM,respectively.Section 7 reports and discusses the numerical results and discussion.Finally,Section 8 includes concluding remarks.
2.Preliminaries
Definition 1.The Reimann–Liuoville integral operator [6] of orderβcan be defined as
Iff∈Cμ,l≥1,β≥0,μ≥-1,m≥0 andq>-1 [6],then the following relations hold as
Definition 2.The fractional derivative off(t) in the Caputo sense[6] can be defined as
3.Time-fractional HAM: a theoretical approach
Let us consider the general operator form of the fractional PDE,
whereSw(X,T) andMβrepresent an unknown function and a nonlinear operator,respectively.
The “zeroth order deformation equation” [46] of the relation(4) is obtained as
If the initial approximation,auxiliary time-fractional linear operatorLβand the control parameter of convergence,i.e.,hare chosen so well,then the homotopy series (7) converges forϱ=1,that is,
Themth order deformation equation can be formed by differentiating the relation (5)mtimes with respect to theϱabout nodeϱ=0 and divided bym! as follows
Employing the inverse operator on Eq.(10),it concludes that
Thus,the series solution (9) converges asm→∞.
4.Application of the HAM
This section implements the above-mentioned HAM to solve a nonlinear T-FPMM arising in the fluid flow processes in fractures and porous matrix in the co-current imbibition and compared the behavior of this phenomenon to the counter-current imbibition in the fractures and the porous matrix.A few of the industrial applications of the imbibition phenomenon can be found in the oil recovery process,biological sciences,composite materials,surface chemistry,printing process,food industry,textile industry,and construction industry,among other industries.
4.1.Mathematical formulation of the problem
The problem considers a porous cylindrical medium in shape with the presence of fractures and porous matrix in it having heterogeneous.The standard interface of the blockx=0 is termed as the imbibition face,and it is not impermeable.It is supposed that the cylindrical block is inclined at a certain angleαwith the ground.Due to the presence of wettability in the medium,a contact angle arises between the phase surfaces.The direction of flow of the wetting phase is in the direction of the non-wetting phase in the cases of co-current imbibition.Whereas in the counter-current imbibition,the flow of wetting and non-wetting phases are in the opposite direction.
Fig.1 shows the preliminary discussion of a fluid flow through the fractures and porous matrix in both the co-current and counter-current imbibition.

Fig.1. Schematic diagram of (a) counter-current;(b) co-current imbibition with some inclination effect.
In this paper,the relative permeability functions for water (Kw)and oil (Ko) are given as Scheidegger [66]
The “Capillary pressure” (pc) in the case of “LeverettJ-function’’ [67] is defined through
For each fluid phase,we describe the conservation of mass equations for the fractured media [60]
in whichqwandqostand for the external source terms that interact with the fractures presents in the porous medium as the flow through fractures is quicker than porous matrix.Now,law the seepage velocity of each fluid phases under the action of capillary pressure and gravity can be illustrated as
By simplifying Eqs.(19),(20) and (22),we get that
Hence,
Thus,the seepage velocityvw,from Eq.(19) is
By virtue ofpw=p-(where p denotes a mean pressure) in Eq.(23),the value ofvTis
Using the value ofvwin Eq.(17),we obtain
Regarding the relations (14),(15) and (16),the continuity equation gives the form
Based on the dimensionless analysis,we introduce the dimensionless variables as
and also,using Eqs.(16) and (30),we obtain
So,the dimensionless configuration of the continuity Eq.(29) can be written as
Eq.(31) illustrates the governing equation for the saturation profiles of water in a co-current imbibition through the water-wet fractured porous media (W-WFPM).
WhenvT=0,we get thatvw=-voand,in this case,the dimensionless form of continuity equation can be written as
Eq.(32) demonstrates the governing equation for the saturation profiles of water in counter-current imbibition through the WWFPM.
Case study
Case 1:Time fractional behaviour of flow co-current imbibition in water wet fractures
To study the time-fractional behaviour with the flow behaviour in the co-current imbibition process in fractures,we fractionalize Eq.(31) in time-fractional order as
Case 2:Time fractional behaviour of flow in co-current imbibition in a porous matrix
Eq.(34) represents the governing equation for saturation profiles of water in a co-current imbibition with gravitational and inclination effect.
Case 3:time fractional behaviour of flow in Counter-current imbibition in water wet fractures
Similarly,to discuss the time-fractional behaviour of flow process in the counter-current imbibition process in fractures,we fractionalize Eq.(32) as
Case 4:Time fractional behaviour of flow in counter-current imbibition in a porous matrix
Eq.(36) denotes the governing equation for saturation profiles of water in counter-current imbibition including appropriate initial condition (IC)
5.HAM approach to the governing problem
With the of IC,the initial approximation of the above problem is taken as
We define the auxiliary linear operator as
Meanwhile,for the nonlinear operator of the relation (33),we have
Themth order deformation equation is
so that
This provides the solution of the relation (33) uptomth approximation as
Thus,we obtain the first approximation form=1 as
such that
Results analysis
Case 1:
Hence,an analytical approximate solution of the relation (33),upto second term estimation is
Eq.(46) demonstrates the saturation profile of wetting phase in co-current imbibition phenomenon in the W-WFPM for a porous medium of time-fractional types Eq.(33).
By applying similar procedure on Eq.(34),we get an approximate analytical solution of Eq.(34),upto two-term approximation as
Case 2:
Eq.(47) represents the saturation profile wetting phase in co-current imbibition phenomenon in the W-WFPM with timefractional Eq.(34).
Case 3:
Eq.(48) illustrates the saturation profile of wetting phase in a counter-current imbibition phenomenon in the W-WFPM for a TFPMM (35).
Case 4:
Eq.(49) denotes the saturation profile of wetting phasein a counter-current imbibition phenomenon in the W-WFPM for a TFPMM (36).
6.Stability analysis
Theorem 1.Let (Y,‖.‖) be a Banach space.Let T a self-map of the banach spaceYsatisfying
for all x,y inYwhere0≤K,0< K′≤1.Then T is said to be Picard T -Stable.
Let us consider the nonlinear Eq.(43) as
Theorem 2.Let us define a self-map T as
The self map is said to be T-stable in L2(0,1) if
Proof.Initially,it is to be shown that the mapTcontains a fixed point.We have
for ∀ (m,k)∈N×N.Based on the property of linearityJ β,we get
From the property of integral and norm,we arrive at
Therefore,we have
where,
Similarly,
where
where
Also,we have
where,
Now putting together expressions (56),(58),(59),(60),(61),(62),(63),(64),(65) into Eq.(55),we obtain
Thus,it impliesThas a fixed point.
Next to show that,the mapTfulfills the conditions as mentioned in Theorem 1.Thus,by substituting
It shows that the nonlinear mappingTsatisfies the conditions of the Theorem 1.As the non-linear mappingTverifies all the conditions of the Theorem 1.Thus,Tis said to be Picard’sT-stable.Hence Proved Theorem 2.□
Following [49],it is straightforward to determine the right value ofhthrough use of theh-curve,which ensures that the solutions are convergent.
Figs.2–5 demonstrate the effect ofhon the solution series,which consists of theh-curve of partial derivatives ofSw(X,T) at(0,0) for cases 1,2,3,and 4.We observe that the valid regions forhare -0.8≤h≤0.2 in Fig.2,-0.7≤h≤0 in Fig.3,-0.45≤h≤-0.2 in Fig.4,and -0.6≤h≤-0.4 in Fig.5.
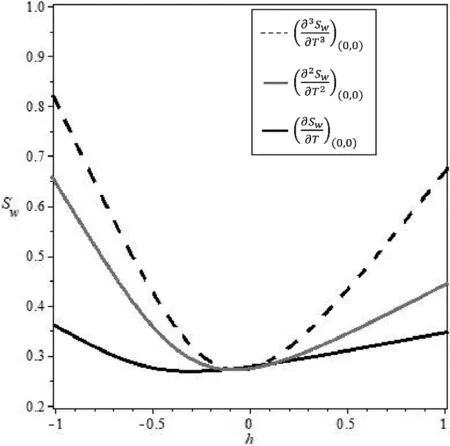
Fig.2. h-curve of partial derivatives of Sw(X,T) for solution obtained in case 1 at (0,0).
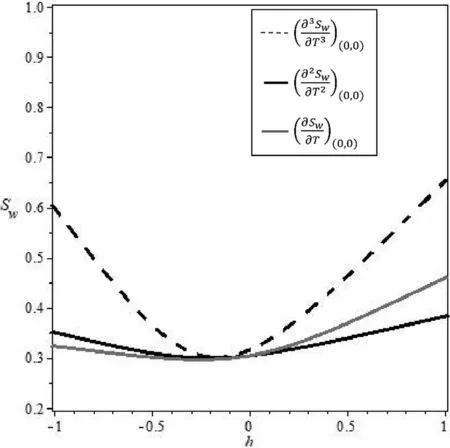
Fig.3. h-curve of partial derivatives of Sw(X,T) for solution obtained in case 2 at (0,0).

Fig.4. h -curve of partial derivatives of Sw(X,T) for solution obtained in case 3 at (0,0).
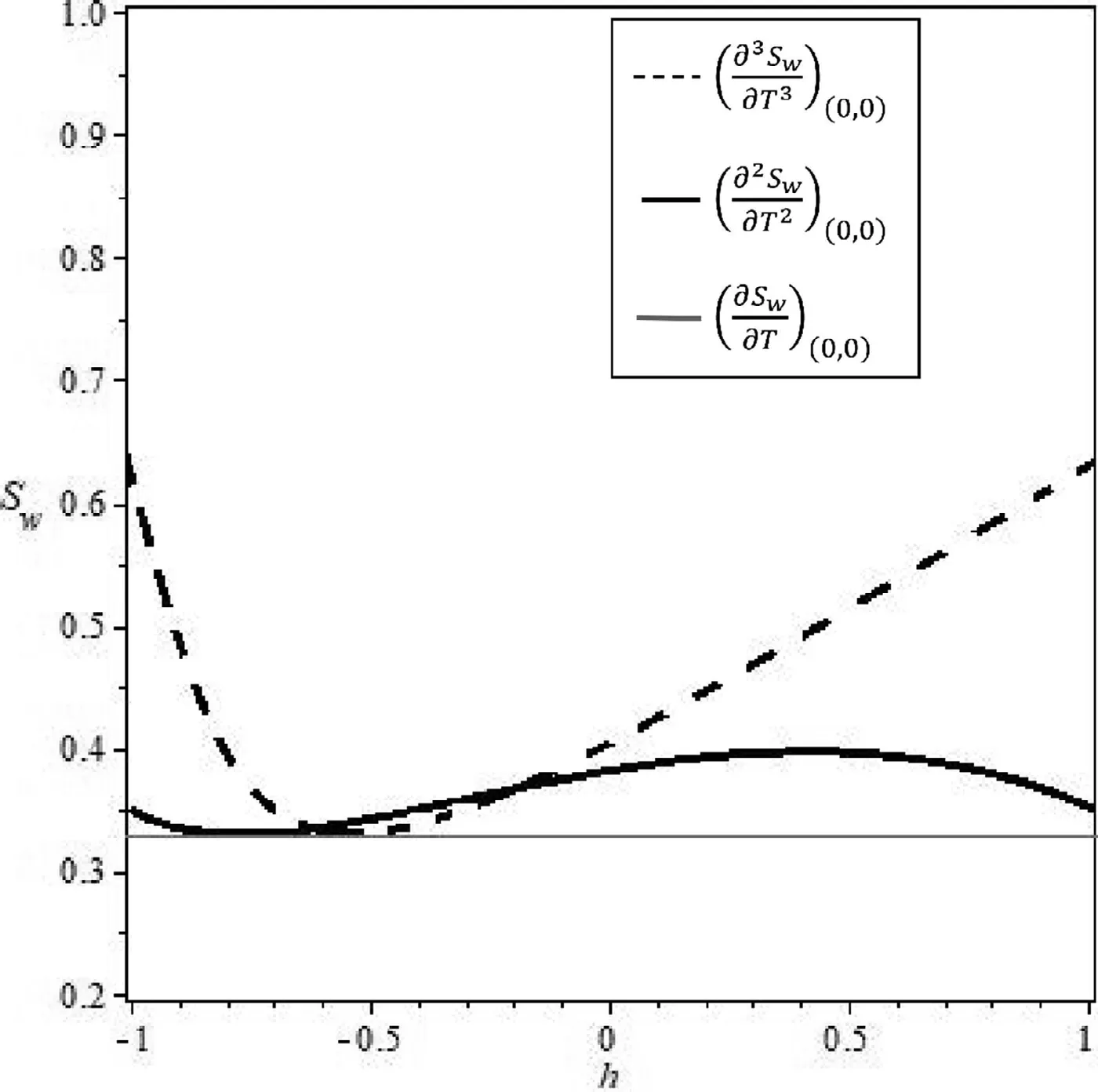
Fig.5. h -curve of partial derivatives of Sw(X,T) for solution obtained in case 4 at (0,0).
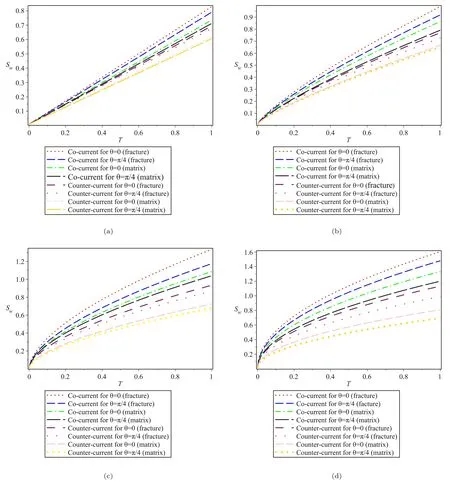
Fig.6. Saturation profiles for “(a) β=1;(b) β=0.8;(c) β=0.6;(d) β=0.5”.

Fig.7. Saturation profiles (θ) for different values of fractional order “(a) β=1;(b) β=0.8; (c) β=0.6;(d) β=0.5” when different wettability state of the medium.
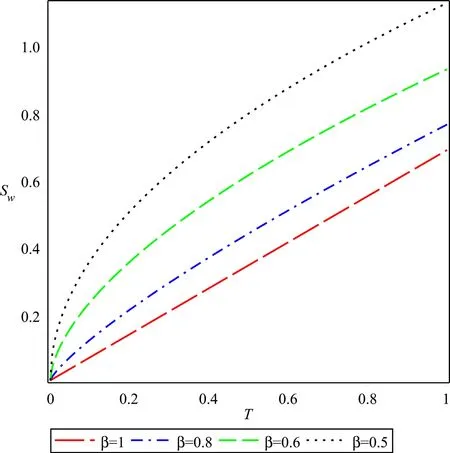
Fig.8. Saturation rate of water,Sw when “strongly water-wet system (θ=0)”,θ in counter-current imbibition for different values β.

Fig.9. Saturation rate of water,Sw when “strongly water-wet system (θ=0)”,θ in counter-current imbibition for different values of β in 3 D.

Fig.10. Saturation rate of water,Sw when “strongly water-wet system (θ=0)”,θ in co-current imbibition for different values of β.
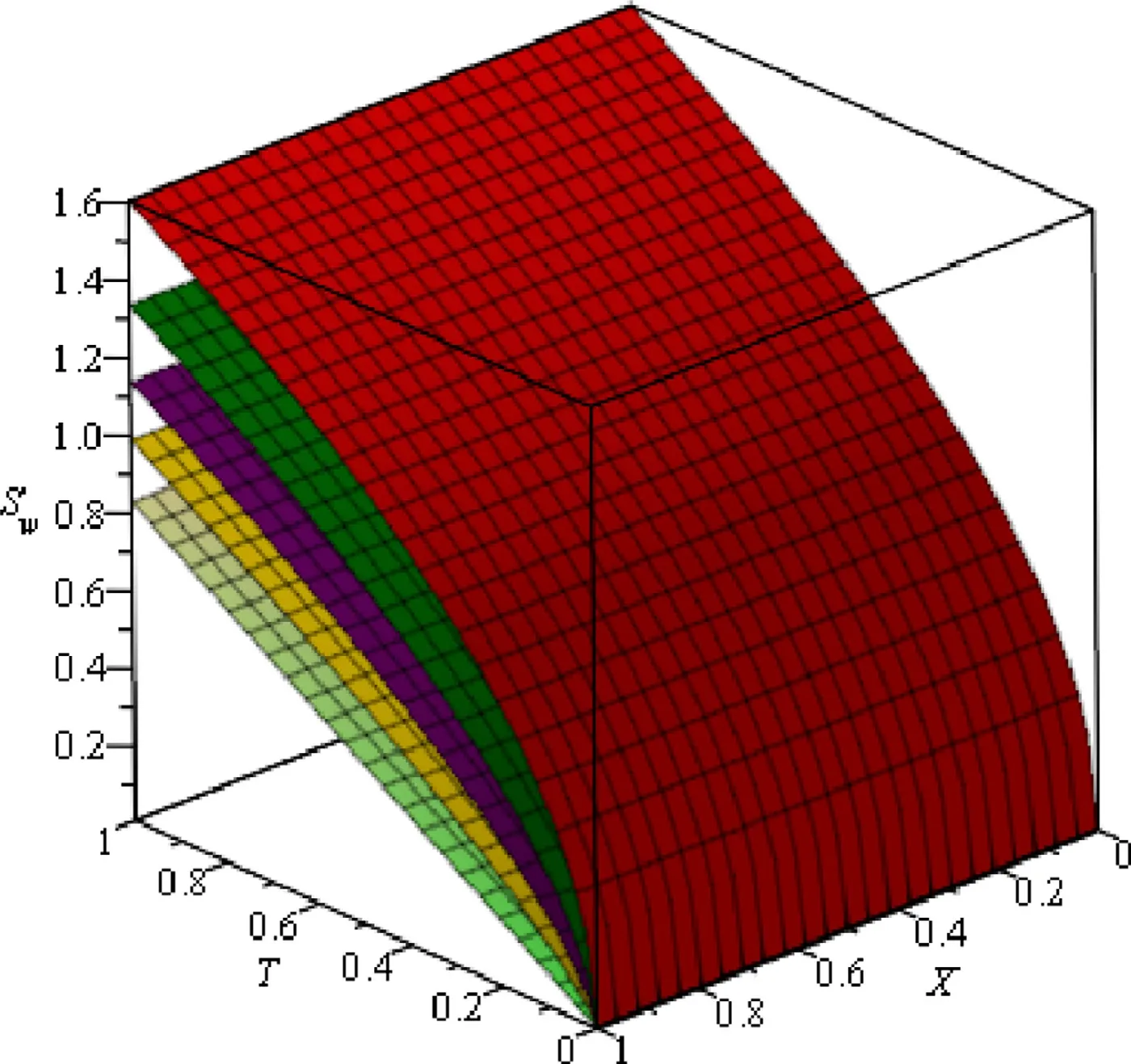
Fig.11. Saturation rate of water,Sw when “strongly water-wet system (θ=0)”,θ in co-current imbibition for different values of β in 3 D.

Fig.12. Saturation profiles of the wetting phase for “(a) β=1;(b) β=0.8;(c) β=0.6;(d) β=0.5”.
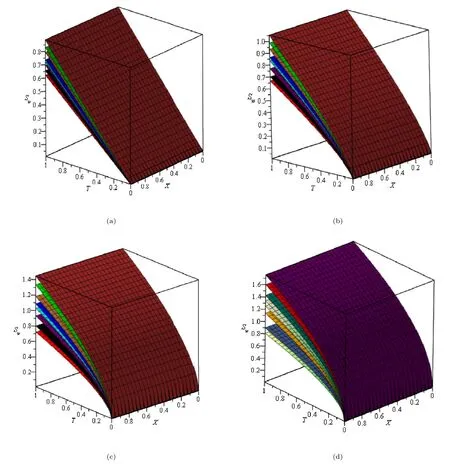
Fig.13. Saturation profiles of the wetting phase for fractional order (a) β=1;(b) β=0.8;(c) β=0.6;(d) β=0.5 in 3 D.
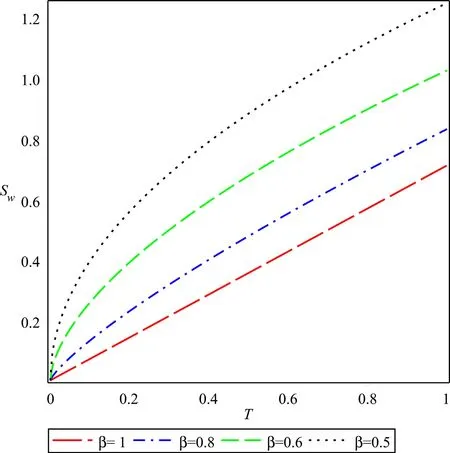
Fig.14. Saturation rate of water,Sw at α=0◦in counter-current imbibition for different values of β.
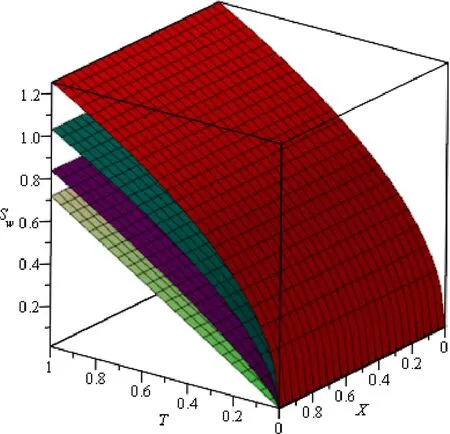
Fig.15. Saturation rate of water,Sw at α=0◦in counter-current imbibition for different values of β in 3 D.
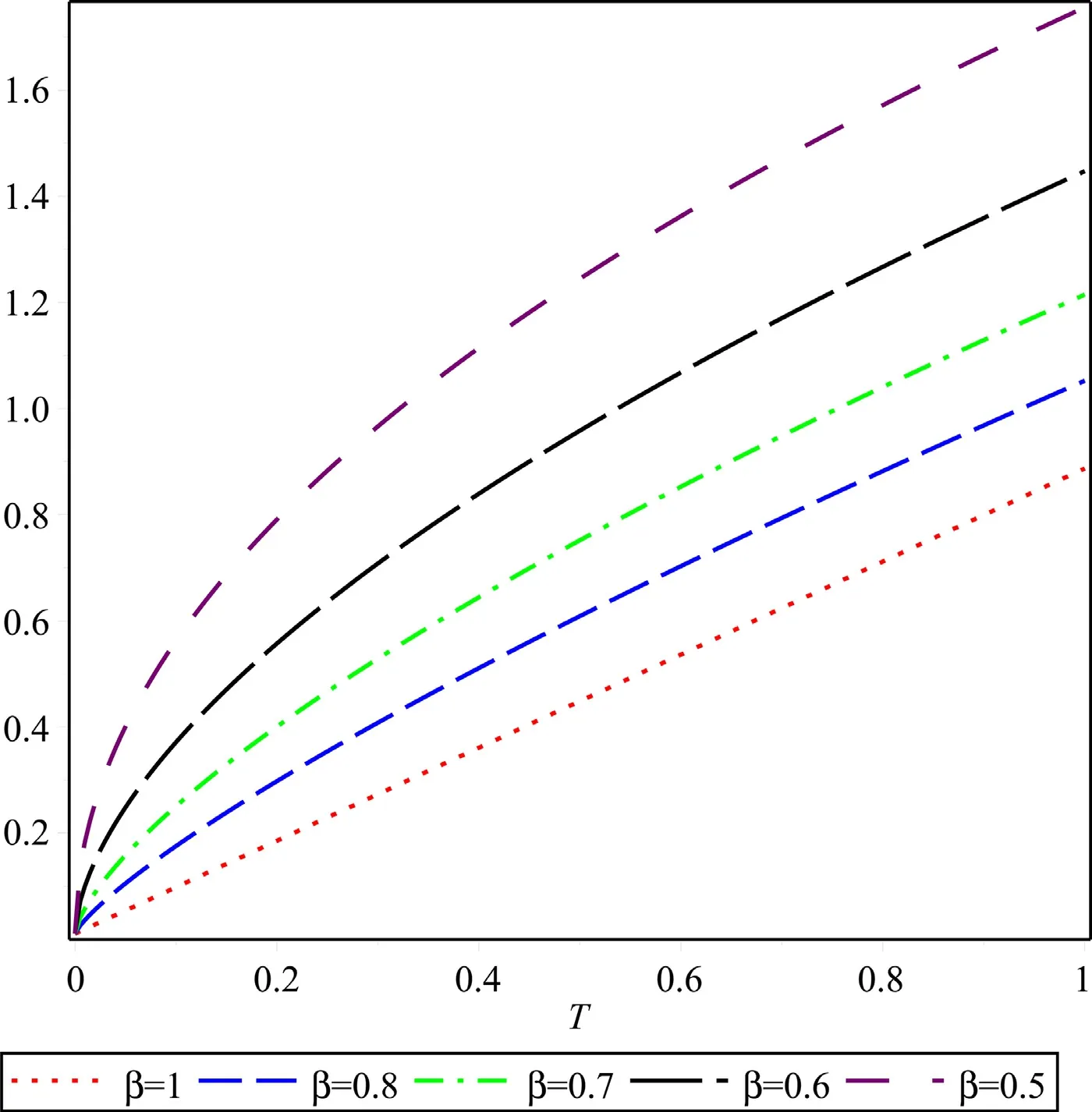
Fig.16. Saturation rate of water,Sw at α=0◦in co-current imbibition for different values of β.
7.Numerical result and discussions
In this section,we study the effects of wettability and inclination on the recovery rate and saturation for distinct fractional valuesβ.All numerical computations were carried out by means of MAPLE program on a desktop with 8 GB memory in Windows 10.
7.1.The saturation profiles of the wetting phase at different wettability with distinct fractional values
Figs.6 -11 shows the deviations of the saturation profile of wetting phase,S wat different wettability and different values of fractional orderβwhich depicts that the saturation profiles behaves well up to the fractional valueβ=0.6.We see that there is a deviation occurs in the saturation profiles for 0 ≤β≤0.5 in the counter-current imbibition whereas the saturation profiles behaves well up to the fractional valueβ=0 .8 and there is a deviation occurs in the saturation profiles for 0 ≤β≤0.7 in the co-current imbibition.Table 1 shows the parametric values of the used parameters.As shown in Table 2 below,we compare the difference in rate of wetting phase saturation (Sw) in the fractured porous medium for the range ofβ∈{0.5,0.6,0.8,1.0} when wettability levels vary.
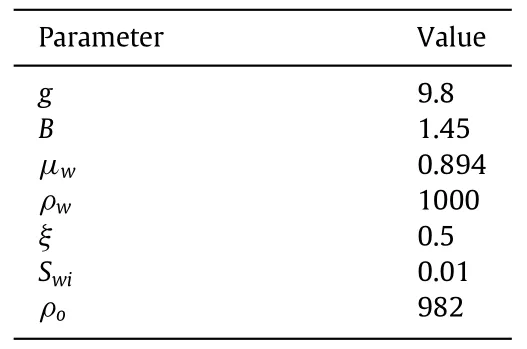
Table 1 The parameters value adopted for graphical and numerical approximation.

Table 2 The rate of wetting phase saturation profile (Sw) in the fractured porous medium for different values of β at varying wettability.
7.2.The saturation profiles of wetting phase at different inclined angles for distinct fractional values
Figs.12–17 display the deviation of the saturation profile of the wetting phase near the inlet (X=0.1) at various inclined planes for different values ofβwhich explain that there is a small deviation in the saturation profile at a distinct inclined angle for 0 .5<β≤1,while it deviates more as the value ofβis smaller than or equal to 0.5 in the counter-current imbibition whereas,there is a small deviation in the saturation profile at a distinct inclined angle for 0.8< β≤1 while it deviates more as the value ofβis smaller than or equal to 0.7 in the co-current imbibition.Table 3 compares the rate of wetting phase saturation profile (Sw) in the fractured porous medium for the values ofβ∈{0.5,0.6,0.8,1.0} when inclination varies.
8.Conclusions
This paper considered the T-FPMM and studied the behavior of the saturation rate with different fractional values and with other parametric effects.From the result and discussion,it can be noticed that there are stimulating effects of time-fractional orders on the recovery rate of the reservoir and the saturation rate of the wetting phase.It occurs in the case ofβ∈(0.5,1] a slight deviation in the wetting phase of the saturation profiles during counter-current imbibition while it is more prominent in the case ofβ∈(0,0.5].By contrast,in the case ofβ∈(0.7,1],we observe a slight deviation in the wetting phase compared toβ∈(0,0.7] during co-current imbibition.Calculations are performed with Maple software.Numerical results benefit researchers are working on the petroleum reservoir problem.
Declaration of Competing Interest
Authors declare that they have no conflict of interest.
杂志排行
Journal of Ocean Engineering and Science的其它文章
- New solitary waves and exact solutions for the fifth-order nonlinear wave equation using two integration techniques
- Optimal Kalman-like filter for a class of nonlinear stochastic systems
- Dynamic quantitative risk assessment of LNG bunkering SIMOPs based on Bayesian network
- New soliton wave solutions of a (2+1)-dimensional Sawada-Kotera equation
- Review of enhancement for ocean thermal energy conversion system
- Prediction of residual tensile strength of glass fiber reinforced polymer bars in harsh alkaline concrete environment using fuzzy metaheuristic models
