标准模型下可证明安全的基于身份的多代理签名*

安徽机电职业技术学院公共基础部 刘莉

1984 年Shamir 首次提出了身份密码学（IBC）的概念，在IBC 系统里，不需要证书，使用用户的标识如姓名、IP 地址、手机号码等作为公钥。用户的私钥由密钥生成中心(简称PKG)根据系统主密钥和用户标识计算得出。用户的公钥由用户标识唯一确定，不需要额外生成和存储，从而用户不需要第三方来保证公钥的真实性。IBC 体系比传统的PKI 体系具有实现成本低、效率较高、运营管理方便等优势。1996 年Mambo 等人提出了代理签名的概念，在一个代理签名方案中，涉及原始签名人、代理签名人和验证人三方。原始签名人授权给代理签名人，代理签名人代表其执行签名。后续几年国外有学者整合了IBC 机制与代理签名，对外提出以身份为基础的代理签名实施方案。2004 年，Hwang 等人在前人的基础上对代理签名进行改进，拓展成为多代理多签名，其含有的原始、代理签名者分别有d(>1)个、n(>1)个[1]。多代理签名方案具有巨大的研究及应用价值，国内外在长期的研究中也出现了很多变种，基于身份的多代理签名方案（IBMPMS）具备密钥管控结构简洁的优势，目前在社交网络系统内实现了规模化应用。尽管IBMPMS 取得的实际研究成绩是值得肯定的，但一些成果仍然存在着安全漏洞，所以基于标准模型下可证明安全的IBMPMS 方案研究很有必要。

基于身份的多代理签名形成的两种形式化安全模型，在具体应用时暴露出两个问题，一个是敌手攻击目标模糊；另一个是敌手分类不完善。在既有安全模型的基础上，对以基于身份的多代理签名为基础的标准安全模型进行了再定义，新模型运用了完善的敌手分类标准，科学定义了各类型敌手的行为方式与攻击目标，在全新安全模型框架的支撑下，设计出一种可靠的多代理签名方案。

1 背景知识介绍

1.1 双线性映射问题

给出大素数p,是p的循环加法群G1与循环乘法群G2，g是G1内的1 个独立生成元，若有e:G1×G1→G2为G1到G2的双线性映射，满足如下几个条件[2]：

（1）双线性：给出任意u,v∈G1与a,b∈Zp*，有（e u a,vb) =e(u,v)ab；

（2）非退化性：e(g,g) ≠1；

（3）可运算性：任意给出u,v∈G1，存在基于多项式时间算法能算出e(u,v)。

关于CDH 问题。对于任何不可预知的a,b∈Zp，给出g,g a,g b∈G1，据此算出gab。CDH 假定：在时间t范畴内，不存在多项式时间的算法,能够基于ε以上的概率求出CDH 问题，那么认定G1之上(ε,t)-CDH 成立。

1.2 IBMPMS 模型

IBMPMS 方案由如下8 个算法共同构成：

（1）系统创建（Setup）：PKG 是该算法执行的主体，输进安全参数k，输出的是公开参数与PKG 持有的主密钥。

（2）用户私钥生成（KeyGen）：PKG 负责执行，输入、输出项分别是params，IDu，用户私钥sku。

（3）基于身份签名（IB-Sign）：这是DelegateUen 与MProxySign 算法实施的基础，输入params，IDu，sku，签名消息m及输出签名σIBS。

（4）身份验证（BISVerify）：输入params，IDu，sku，m及σIBS，输出T、⊥分别代表的是接受签名、签名无效[3]。

（5）代理授权签名（DelegateUen）：原签名者负责实施该算法，输入项包括 params，原始签名ID0及其持有的私钥sku，代理者身份列表，授权书编号w，输出项是代理授权签名δ。

（6）授权验证（DelegateVer）：各位代理人员分别实施。

（7）多代理签名（MProxySign）：全部代理人员共同实施该算法，输入项包括params，ID0，及对应的私钥，ω,δ,m输出项为多代理多签名σ[4]。

（8）多代理验证（MProxyVerify）：验证者是该算法的执行主体，按照一定规程依次输入params，ID0，，ω,δ,m,σ，输出T、⊥依次表示接受签名、签名信息无效。

1.3 IBMPMS 安全模型

本文以Paterson 等形成的标准化签名模型作为理论基础，融合拓展Huang、Boldyreva 的模型，提出了IBMPMS 方案的新标准安全模型。IBMPMS 方案应具有的安全属性有身份可辨识性、可检验性、不可伪造性和不可否认性。

结合前人的研究成果，合理定义了模型的敌手A∈{A2,A3,A4}（A2,A3,A4即Gu-IBMPS 模型允许敌手）和挑战者之间进行的游戏（IBMPMS-EUF-CMA Game），进而更加合理的模拟方案自身具有的不可伪造属性。鉴于不考虑标准签名（A1）敌手被用在模拟签名方案的安全性方面，本文的标准签名直接运用了Paterson 机制，已经有充分的论据证实该机制符合安全要求，故而本文建立的安全模型不必考虑敌手A1[5]。

2 IBMPMS 的设计

陈明[4]在研究中制定了基于身份的多代理签名方案（CY-IBMPMS），并清楚定义了符合该方案分析形式的标准化模型。本文在CY-IBMPMS 方案基础上，有效拓展了原始签名者的身份集，提出了一种新的IBMPMS 方案。和传统IBMPMS 方案相比，提出的新方案安全假设强度降低，方案的安全性直接转变成求算CDH 问题[6]。

本方案执行过程中无需组员之间相互传输参数信息，只需组长采集、聚合各个组员的签名信息，这种运作模式大大地减少了通信成本。方案包含的算法如下：

Setup：输入一个安全的参数k，PKG 自动生成并公示公开参数。

params={G1,G2,e,g1,g2,Q,u',U,w',W,m',M,H1,H2}。g是G1的生成元，g2∈G1与α∈Zp， PKG 公钥是g1=ga与Q=e(g1,g2)；PKG 主密钥可以表示成g2a；u',w',m'∈G1。向量U={ui},W={wi},M={mi}，长度依次是nu,n w,nm，ui,wi,mi∈G1。H1,H2为安全Hash 函数[7]。

KeyGen：输入项是用户身份ui，PKG选择ri∈Zp，生成用户私钥基于前期设置好的安全信道把ski传送给ui。ui的对应长度是nu，Vi⊆{1,2,...,nu}代表的是nu内比特值是1 的部位d的集。

Sign/Verify：运用PS-IBS 签名[7]以及验证算法共同执行该过程。

各个ui∈任意选择si∈Zp，运算：命令δi,3=ski,2，随后把δi,1,δ i,2,δi,3逐一传送给uo。X⊆{1,2,...,nu}表示的是H1(W)内比特值是1 的部位k的集。

（2）接收到全部<δi,1,δi,2,δi,3>以后，uo运算完整的输出代理权签名信息δ=<δ1,δ2,δ3>，将其逐一传送给各个代理签名人员。

（3）MProxy MSign：完整地接收δ以后，基于uj∈检测验证e(δ1,g)=Qd。

（4）MPMSVerify：精准接收σ、w与以后，检验者先检测判断授权书W是否有效，如果能断定其为无效，那么就会输出⊥，否则通过运算以检验式（1）成立与否：

如果经检验能够确定以上等式成立，则输出T，否则输出项为⊥。

3 IBMPMS 的安全性分析

3.1 准确性

当式（2）、式（3）成立时，分别代表用户私钥、代理权签名及其检测验证结果有效[9]：

3.2 不可伪造性

假定A∈{A2,A3}最多执行KeyGen、DelegateGen与MProxyMSign询问分别为qe,q d,qs次，概率高于ε时才能成功挑战IBMPMS-EUF-CMA Game，若(ε',t' )-CDH等式成立，那么本文建立的IBMPMS 机制符合(ε,t,qe,qd,qs)IBMPMS-EUF-CMA 的安全标准如式（4）所示：

ρ,τ,ϕ依次代表的是G1之上的乘运算、指数运算以及对运算时间，nu,n w,nm分别表示用户ID、代理授权文书以及签名消息本体的比特度。

3.3 分析和对比

既往国外很多学者提出的IBMPMS 方案运用了基于随机预言的可证明性安全模型，但其实在客观世界内还不能达到随机预言机，这就为敌手辨识模拟情景与实际情景创造了便利性。鉴于以上情况，本课题研究中提出了标准化安全模型，该模型采用建造特殊的陷门函数形式，模拟全程敌手均不能准确区别各类情景，这就预示着其具备超强的安全规约性能。如表1 所示为几种常见IBMPS 方案的对比情况[10]。

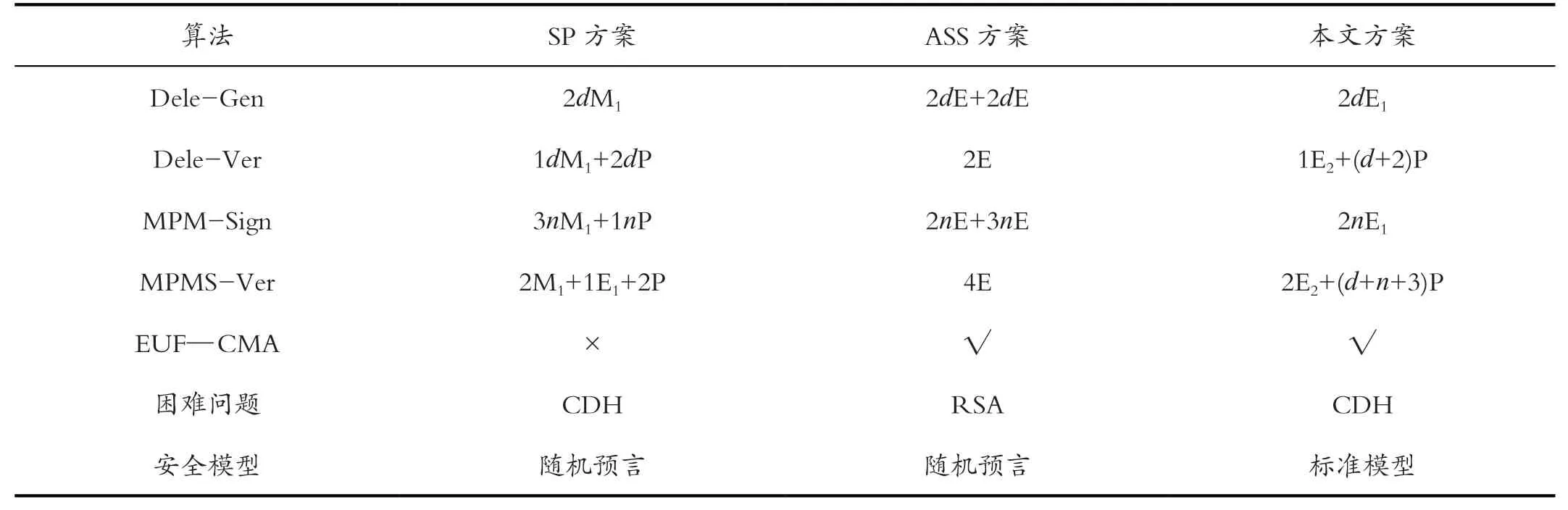
表1 几种常见IBMPMS 方案的对比Tab.1 Comparison of several common IBMPMS schemes

综合分析，ASS-IBMPMS 方案在运算性能方面稍有优越性，但该方案执行的广播通信、单播通信次数均达到了d+n次，而本文设计的新方案只需要进行d+n次的单播通信，因此，ASS-IBMPMS 方案实施期间通信成本支出较高。

4 结语

本文在陈明等人研究的基础上，对原始签名用户集进行了拓展，提出了一种新的基于身份的多代理、多签名的方案，并建立了IBMPMS-EUF-CMA 这一新的标准安全模型，在该模型下检测新代理签名方案，分析表明该方案自身具有较高的不可伪造性，这是其实现不可否定性、身份可辨识性与防滥用性的重要基础。通过几种常见IBMPMS 方案的比较结果可以看出，新建立的安全模型功能更加完善，在标准模型下基于身份的多代理签名可以验证是一种安全、可靠的身份密码方案。