Specific wave profiles and closed-form soliton solutions for generalized nonlinear wave equation in (3+1)-dimensions with gas bubbles in hydrodynamics and fluids

Sachin Kumar ,Ihsanullah Hamid ,M.A.Abdou

a Department of Mathematics, Faculty of Mathematical Sciences, University of Delhi, Delhi 110 0 07, India

b Department of Mathematics, College of Sciences, University of Bisha, P.O. Box 344, Bisha 61922, Saudi Arabia

c Physics Department, Faculty of Science, Mansoura University, Mansoura 35516, Egypt

Keywords: Closed-form solutions Dynamical wave patterns Analytic solutions Nonlinear wave equation GERF Method Solitary waves Solitons

ABSTRACT Nonlinear evolution equations (NLEEs) are frequently employed to determine the fundamental principles of natural phenomena.Nonlinear equations are studied extensively in nonlinear sciences,ocean physics,fluid dynamics,plasma physics,scientific applications,and marine engineering.The generalized exponential rational function (GERF) technique is used in this article to seek several closed-form wave solutions and the evolving dynamics of different wave profiles to the generalized nonlinear wave equation in (3+1)dimensions,which explains several more nonlinear phenomena in liquids,including gas bubbles.A large number of closed-form wave solutions are generated,including trigonometric function solutions,hyperbolic trigonometric function solutions,and exponential rational functional solutions.In the dynamics of distinct solitary waves,a variety of soliton solutions are obtained,including single soliton,multi-wave structure soliton,kink-type soliton,combo singular soliton,and singularity-form wave profiles.These determined solutions have never previously been published.The dynamical wave structures of some analytical solutions are graphically demonstrated using three-dimensional graphics by providing suitable values to free parameters.This technique can also be used to obtain the soliton solutions of other well-known equations in engineering physics,fluid dynamics,and other fields of nonlinear sciences.

1.Introduction

Liquids with gas bubbles,which are abundant in science,engineering,physics,nature,and life,have attracted people’s attention.Bubble-liquid mixture equations have been presented to describe the propagation of weakly nonlinear waves in liquids containing gas bubbles [1,2].Many nonlinear wave phenomena seen in nature may be described using analytical solutions;consequently,understanding the exact solutions of NLEEs is very important.Many different kinds of analytic solutions for nonlinear evolution equations(NLEEs) have been investigated and used in nonlinear optics,fluid mechanics,and plasma physics in the literature,including the soliton,lump,breather,rogue wave,and periodic wave solutions and various other form solutions [3–29,86–92,85,93].

There are several approaches to finding analytical solutions for NLEEs,including Lie symmetry analysis [30–38],Darboux transformation technique [39],Bäcklund transformation technique [40],Hirota bilinear approach [41,42],Generalized exponential rational function (GERF) technique [43] and other mathematical techniques[44–68].

The fundamental concept behind using the GERF technique to solve an equation is to utilize an appropriate variable change to convert a partial differential equation into an ordinary differential equation (see [69–72]).Liquids containing gas bubbles are frequent in many disciplines,including medical sciences and engineering,as non-linear phenomena in nature.The research on liquid containing gas bubbles has always been the focus of nonlinear wave research,and has aroused the interest of many researchers (see [73–76]).In this investigation,we examine the generalized constant-coefficient nonlinear wave equation in (3+1) dimensions with gas bubbles in fluids given by [77] as

whereu=u(x,y,z,t),hi(i=1, 2, 3, 4, 5) are free constants.Eq.(1) incorporates several governing physical equations as special reductions by picking some relevant values forhi,as shown below:

•Forh1=-6,h2=1,h3=0, &h4=h5=3,Eq.(1) has been reduced to the well-known constant-coefficient Kadomtsev-Petviashvili equation [78] in (3+1)-dimensions

is investigated by Ablowitz and Segur.Its threewave solitontype solutions,Wronskian and Grammian solutions and a wide class of Pfaffianized systems of the equation are investigated by Ma,Xia and Zhu [79,80].

•Forh1=h2=1,h3=0,h4=1, &h5=0,Eq.(1) has been degenerated to the (2+1) -dimensional constant-coefficient Kadomtsev-Petviashvili equation [81],

which describes the weakly nonlinear long waves in a weakly dispersive medium.Stability of the solitary wave solutions for Eq.(3) has been investigated [81].

•Forh1=6,h2=1,h3=0, &h4=h5=,Eq.(1) has been reduced into a (3+1) -dimensional shallow water wave equation[82],

is given for a description of the pressure waves in admixture liquid and gas bubbles taking into consideration the viscosity of liquid and the heat transfer.Some exact solutions for the nonlinear evolution equation are presented by the application of the Hirota method [82].

•Forh1=1,h2=,h3=-1, &h4=h5=,Eq.(1) has been shrink into a (3+1) -dimensional shallow water wave equation[82],

which describes the nonlinear waves in a fluid with gas bubbles.Stationary solitary wave solutions for Eq.(5) and Lie symmetry approcah,optimal system and invariant solutions have been investigated [82,83].

•Forh1=6,h2=1 &h3=h4=h5=0,Eq.(1) has been bring to the (1+1) -dimensional KdV equation [84],

is obtained to describe several complex physical phenomena,such as plasma physics,optical fibers,fluid dynamics,ionacoustic waves,lattice dynamics.

For the generalized (3+1)-dimensional constant-coefficient with non-linear wave Eq.(1),Lumps,multiple soliton solutions,infinite conservation laws,periodic wave solutions,Lump wave and hybrid solutions have been studied using Bäcklund transformation in ref [73–75].

As a consequence of the abovementioned references,the generalized (3+1)-dimensional nonlinear wave equation will be investigated using the GERF technique.The prime objective of this work is to develop a large number of analytical soliton solutions to the nonlinear wave equation,as well as to illustrate the dynamics of some generated solutions.We derive a variety of closed-form solutions to the governing equation using the GERF technique.Among the most recent solitonic wave solutions are multi-wave fronts,periodic form solitons,bell-shaped profiles,traveling wave forms,kink-wave forms,and nonlinear behavior form solutions.There are also several dynamical solitonic shapes of achieved solutions demonstrated via numerical simulation.As a result,our newly generated analytic wave solutions are new and never reported in the literature.Consequently,these newly revealed facts will be productive and beneficial in understanding the different solitonic wave profiles in liquid-containing gas bubbles caused by various known constant parameters.

This article is organized as follows.In Section 2,we outline the GERF approach.In Section 3,abundant soliton solutions of the generalized non-linear wave equation Eq.(1) in (3+1)-dimensions with gas bubbles in liquid are obtained by using the GERF method with symbolic computation.In addition,the different dynamic wave structures of the solution are explained in this section.Section 4,Results and discussion presents graphical illustrations of several soliton solutions using symbolic computational work with Mathematica.Finally,some conclusions are given in Section 5.

2.The GERF methodology

The GERF approach is summarized in the following points:

Stage1.We shall consider a nonlinear PDE of the type

Employingψ=ψ(χ) along withχ=kx+my-ct,we achieve

wherek,mandware free constant parameters that will be determined later.

Stage2.Following that,the explicit solution to Eq.(8) is provided.

wherel1,l2,l3,l4, andj1,j2,j3,j4are real/complex numbers,and Eq.(7) is represented as

Simultaneously,the coefficientsA0,Ak,Bk(1≤k≤M) will be computed since this (10) satisfies (8).In addition,Mis a positive integer which could be determined and used the homogeneous balancing approach.

Stage3.The polynomial equationis calculated by plugging Eq.(10) into Eq.(8) and clustering all components.Mathematica is used to obtain a set of algebraic equations forln,jn(1≤n≤4), andk,m,c,A0,A1,B1,which equate every coefficient ofPto zero.

Stage4.To extract the solitary wave solutions of Eq.(7) by calculating the outcomes in Stage 3 and afterwards entering explicit solutions into (10).

3.Closed-form wave solutions

This section uses the GERF approach to present abundant closed-form wave solutions of the governing equation (1).As aforementioned,the first Stage in solving Eq.(1) is to transform it from a nonlinear PDE to an ODE.Due to the obvious new variable definitions provided below,these improvements will be possible as

wherek,m,pandcare parameters which are arbitrarily unknown.One obtains

After integrating the Eq.(12) twice and zeroing the constant,we will get the following result:

By using homogeneous balance principle in (13),we balanceu2withu′′,yieldingM=2.Considering all of the above requirements,the scheme is presented in the representative form given below:

The following solitonic wave-form solutions are generated after performing the essential phases of the procedure outlined in Section 2.

Group 1

Forl=[i,-i, 1, 1],andj=[i,-i,i,-i].Use such constants in Eq.(9),returns

Set 1:

By putting the obtained from previously set values and equation (15) into (14),we get

As a consequence,we obtain

Set 2:

By putting the obtained from previously set values and equation (15) into (14),we get

As a consequence,we obtain

Set 3:

By putting the obtained from previously set values and equation (15) into (14),we get

u(χ)=-B1cot (χ)+B2cot2(χ).

As a consequence,we obtain

Set 4:

A0=A2=B2=0, &A1,B1=arbitrary.

By putting the obtained from previously set values and equation (15) into (14),we get

u(χ)=-B1cot (χ)-A1tan (χ).

As a consequence,we obtain

Family 2

Forl=[1-i,-1-i,1,-1],andj=[-i,i,-i,i].Use such constants in Eq.(9),returns

Set 1:

A0=A1=0, &A2,B1,B2=arbitrary.

By putting the obtained from previously set values and equation (20) into (14),we get

As a consequence,we obtain

Set 2:

By putting the obtained from previously set values and equation (20) into (14),we get

As a consequence,we obtain

Set 3:

By putting the obtained from previously set values and equation (20) into (14),we get

As a consequence,we obtain

Family 3

Forl=[-3,-2,1,1],andj=[0,1,0,1].Use such constants in Eq.(9),returns

Set 1:

By putting the obtained from previously set values and equation (24) into (14),we get

As a consequence,we obtain

Set 2:

By putting the obtained from previously set values and equation (24) into (14),we get

As a consequence,we obtain

where

Set 3:

By putting the obtained from previously set values and equation (24) into (14),we get

As a consequence,we obtain

where

Set 4:

By putting the obtained from previously set values and equation (24) into (14),we get

As a consequence,we obtain

Set 5:

By putting the obtained from previously set values and equation (24) into (14),we get

As a consequence,we obtain

Set 6:

By putting the obtained from previously set values and equation (24) into (14),we get

As a consequence,we obtain

Family 4

Forl=[1,0,1,1],andj=[1,0,1,0].Use such constants in Eq.(9),returns

Set 1:

By putting the obtained from previously set values and equation (31) into (14),we get

As a consequence,we obtain

where

Set 2:

By putting the obtained from previously set values and equation (31) into (14),we get

As a consequence,we obtain

Family 5

Forl=[1,1,-1,1],andj=[1,-1,1,-1].Use such constants in Eq.(9),returns

Set 1:

By putting the obtained from previously set values and equation (34) into (14),we get

u(χ)=A0-A1coth (χ)-B1tanh (χ).

As a consequence,we obtain

Set 2:

By putting the obtained from previously set values and equation (34) into (14),we get

As a consequence,we obtain

Set 3:

By putting the obtained from previously set values and equation (34) into (14),we get

As a consequence,we obtain

Set 4:

By putting the obtained from previously set values and equation (34) into (14),we get

As a consequence,we obtain

Set 5:

By putting the obtained from previously set values and equation (34) into (14),we get

As a consequence,we obtain

Family 6

Forl=[-3,-1,1,1],andj=[1,-1,1,-1].Use such constants in Eq.(9),returns

Set 1:

By putting the obtained from previously set values and equation (40) into (14),we get

As a consequence,we obtain

Set 2:

By putting the obtained from previously set values and equation (40) into (14),we get

As a consequence,we obtain

Family 7

Forl=[-1,1,1,1],andj=[1,-1,1,-1].Use such constants in Eq.(9),returns

Set 1:

By putting the obtained from previously set values and equation (43) into (14),we get

u(χ)=-B1coth (χ)+B2coth2(χ).

As a consequence,we obtain

Set 2:

By putting the obtained from previously set values and equation (43) into (14),we get

u(χ)=A0-B1coth (χ).

As a consequence,we obtain

Family 8

Forl=[1,-3,-1,1],andj=[1,-1,1,-1].Use such constants in Eq.(9),returns

Set 1:

By putting the obtained from previously set values and equation (46) into (14),we get

As a consequence,we obtain

Set 2:

By putting the obtained from previously set values and equation (46) into (14),we get

As a consequence,we obtain

Set 3:

By putting the obtained from previously set values and equation (46) into (14),we get

As a consequence,we obtain

Family 9

Forl=[2+i,2-i,1, 1],andj=[-i,i,-i,i].Use such constants in Eq.(9),returns

Set 1:

By putting the obtained from previously set values and equation (50) into (14),we get

As a consequence,we obtain

Set 2:

By putting the obtained from previously set values and equation (50) into (14),we get

As a consequence,we obtain

Set 3:

By putting the obtained from previously set values and equation (50) into (14),we get

As a consequence,we obtain

Fig.1. 3 different evolving wave-forms of solution u1(x,y,t) are portrayed in three-dimensional postures with k=0.1, m=0.01, p=.1, h1=1, h2=-5, h3=-2, h4=3, h5=0.7, and t=0.1.

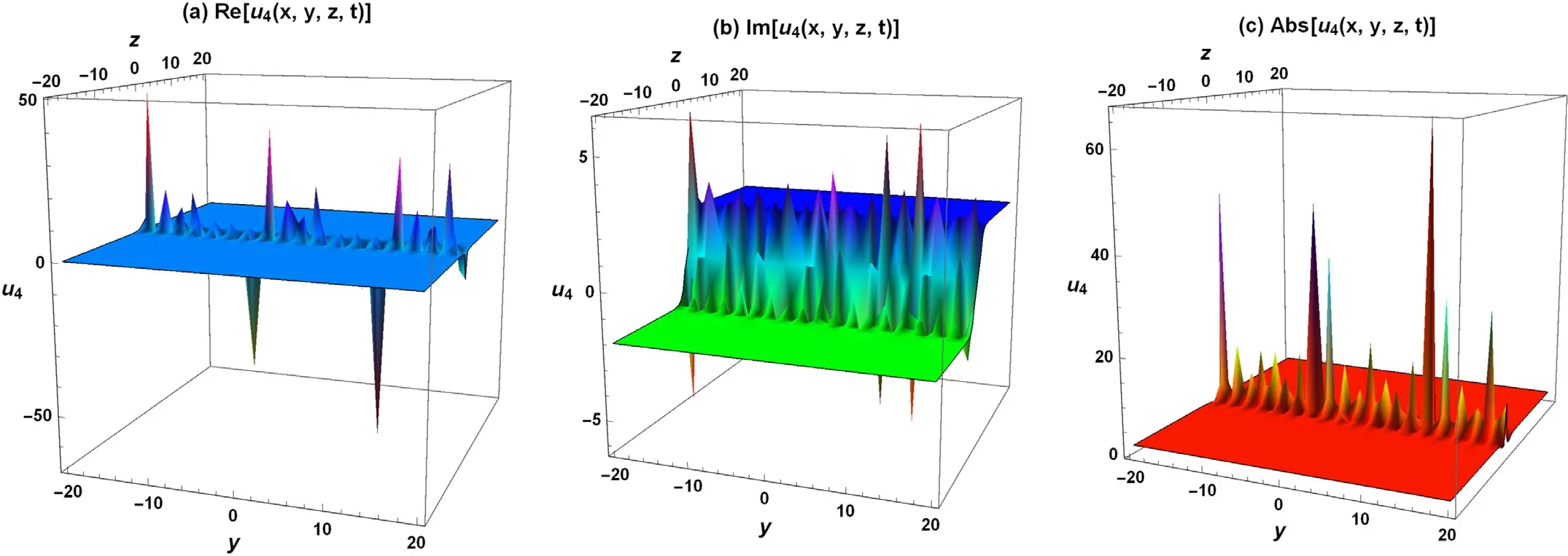
Fig.2. 3 different evolving wave-forms of solution u4(x,y,t) are portrayed in three-dimensional postures with c=2, m=3, B1=1, A1=3, h4=0.5, h5=10, and t=0.1.

Fig.3. 3 different evolving wave-forms of solution u8(x,y,t) are portrayed in three-dimensional postures with c=1, m=0.1, A0=0.5, A1=0.1, A2=0.7, B1=2, B2=1, h4=3, h5=0.7, and t=1.

4.Results and discussion

Fig.4. 3 different evolving wave-forms of solution u13(x,y,t) are portrayed in three-dimensional postures with c=2, m=10, B1=0.2, h4=3, h5=0.7, and t=10.

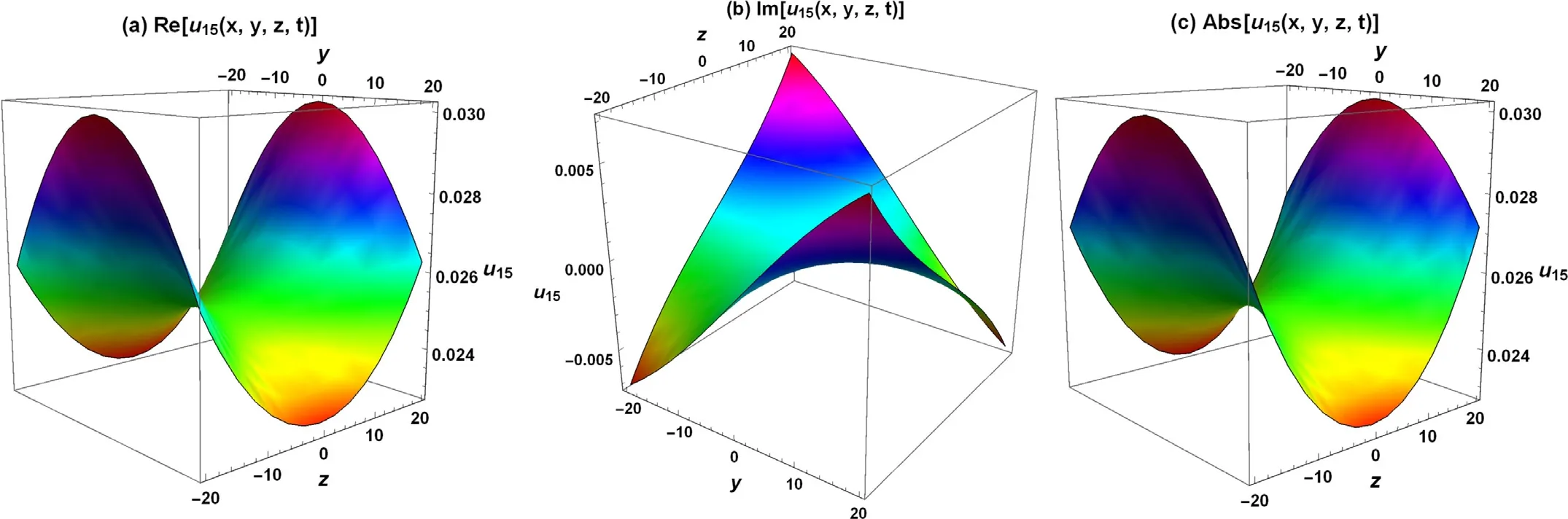
Fig.5. 3 different evolving wave-forms of solution u15(x,y,t) are portrayed in three-dimensional postures with c=1, m=0.03, A1=0.1, h4=2, h5=1, and t=0.01.

Fig.6. 3 different evolving wave-forms of solution u16(x,y,t) are portrayed in three-dimensional postures with c=1, m=0.1, A0=0.1, A1=1, B1=-5, h4=3, h5=0.7, and t=0.1.

This section depicts the nonlinear behavior of evolving wave profiles for many analytic wave solutions to the nonlinear wave equation.Three-dimensional wave-form profiles and the graphical approach of illustrating various solitonic structures of generated solutions are commonly used to explain various physical phenomena.The derived solutions to the original nonlinear wave equation are depicted as different wave profiles including bright and dark soliton,singular wave-form profiles,combo singular waves,kink waves with various solitons,and other wave profiles with the help of numerical simulations via mathematical software Mathematica.Numerical simulation and symbolic computation are exploited to depict the evolving dynamical illustrations of various closed-form solutions as well as new wave-front sketches.Figs.1,2,3,4,5,6,7,8,9 and 10 depict various interesting solitary wave profiles of the(3+1)-dimensional wave equation using three-dimensional graphics and appropriately involved constant parameters.Various derived solutions to the original nonlinear wave equation are represented graphically in the captions/descriptions of each figure.The generalized exponential rational function technique was heavily employed in this research to depict diverse dynamical wave patterns of computed analytical wave solutions to the considered equation.Therefore,a large number of wave solutions have been obtained that might be used to best reveal the underlying wave profiles of complex physical systems in fields such as marine engineering,ocean physics,optical physics,plasma physics and hydrodynamics,fluid dynamics,nonlinear dynamics,marine engineering,and so on.

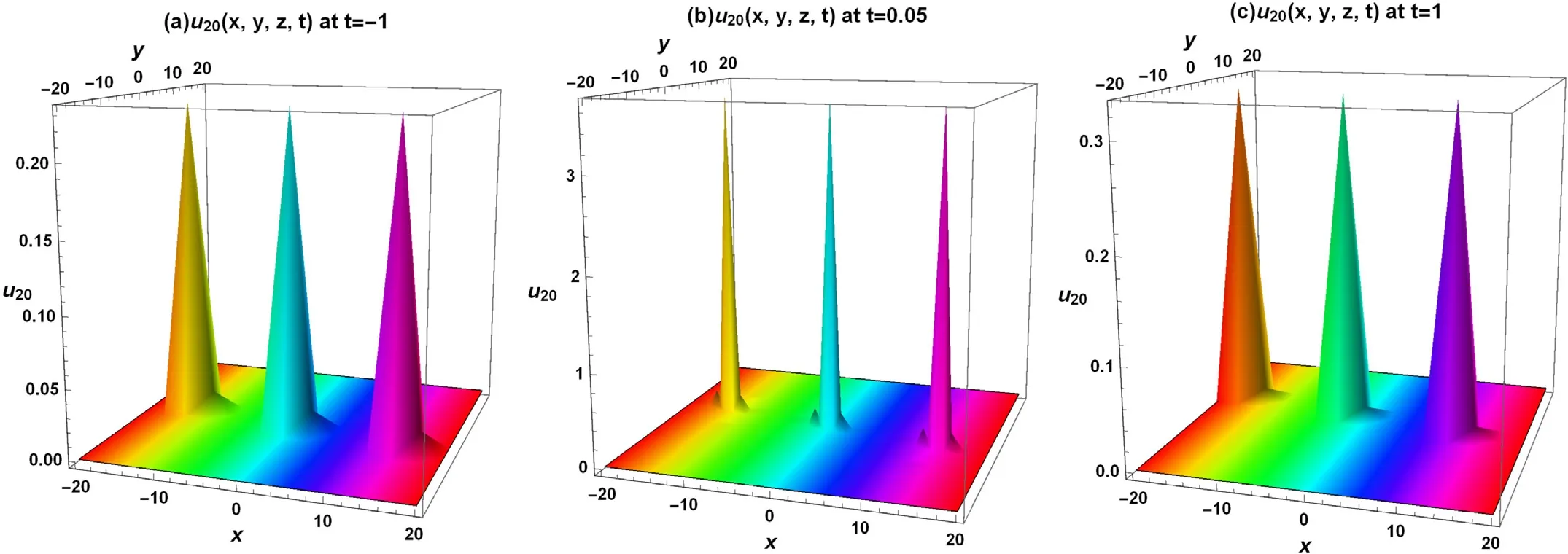
Fig.7. 3 different evolving wave-forms of solution u20(x,y,t) are portrayed in three-dimensional postures with k=2, m=10, p=. 75, h1=0.1, h2=0.01, h3=0.15, h4=0.5, h5=0.02, and z=1.

Fig.8. 3 different evolving wave-forms of solution u22(x,y,t) are portrayed in three-dimensional postures with c=0.1, m=0.2, A1=10, B1=3, B2=5, h4=5, h5=3, and t=0.01.

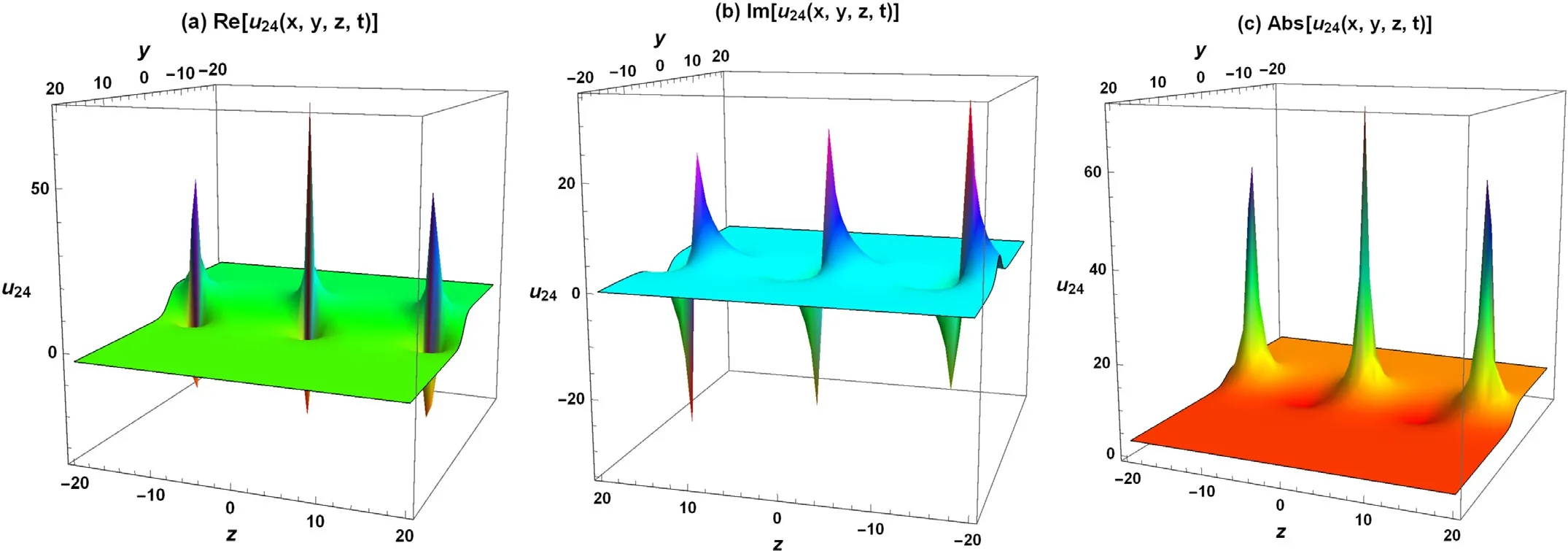
Fig.9. 3 different evolving wave-forms of solution u24(x,y,t) are portrayed in three-dimensional postures with c=-1, m=0.3, A0=2, B1=5, h4=3, h5=7, and t=1.

5.Conclusion

In conclusion,we studied the generalized nonlinear wave equation in (3+1)-dimensions,occurring in liquid with gas bubbles,and achieved the thirty solitonic solutions,which were extensively investigated in the article employing the GERF technique and computerized symbolic work.Figs.1,2,3,4,5,6,7,8,9 and 10 show several of these generated solutions that are adequate for modeling the wave propagation of perfect traveling waves.Multiplepeak waves,bright and dark solitons,combination singular waveform profiles,multi-wave patterns,and perfect solitary waves are among the recently discovered solutions to the governing equation.It should be emphasized that all produced solutions are validated for authenticity/trustworthiness by simply replacing them with the considered equation (1).All of these acquired results with varied dynamical wave shapes and free constants are considered major accomplishments that will be tremendously valuable in studying the dynamical patterns of liquid with gas bubbles.Some of the soliton solutions obtained are single soliton,combo-singular soliton,and various specific wave-form profiles that are completely different from the previous author’s work [93].These soliton wave profiles have also been presented in 3D graphics using numerical simulations in Mathematica software.These newly formed nonlinear wave equation findings/solutions have a wide range of scientific implications,including hydrodynamics,marine engineering,fluid dynamics,ocean engineering,plasma physics,nonlinear dynamics,and a variety of other engineering physics and nonlinear sciences fields.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

The author,Sachin Kumar,is grateful to the Institution of Eminence,University of Delhi,India,for providing financial assistance for this research through the IoE scheme under Faculty Research Programme (FRP) with Ref.No./IoE/2021/12/FRP.