New exact solutions of the Mikhailov-Novikov-Wang equation via three novel techniques

Arzu Akulut ,Melike Kpln ,Mohmmed K.A.Kr ,

a Mathematics-Computer Department, Art-Science Faculty, Eski ¸s ehir Osmangazi University, Eski ¸s ehir, Turkey

b Department of Computer Engineering, Engineering and Architecture Faculty, Kastamonu University, Kastamonu, Turkey

c Institute of Mathematical Sciences, Faculty of Science, University of Malaya, Kuala Lumpur 50603, Malaysia

Keywords: Exact solutions Generalized Kudryashov method Modified extended tanh-function method Symbolic computation PDEs

ABSTRACT The current work aims to present abundant families of the exact solutions of Mikhailov-Novikov-Wang equation via three different techniques.The adopted methods are generalized Kudryashov method (GKM),exponential rational function method (ERFM),and modified extended tanh-function method (METFM).Some plots of some presented new solutions are represented to exhibit wave characteristics.All results in this work are essential to understand the physical meaning and behavior of the investigated equation that sheds light on the importance of investigating various nonlinear wave phenomena in ocean engineering and physics.This equation provides new insights to understand the relationship between the integrability and water waves’ phenomena.

1.Introduction

Nonlinear phenomena are observed in many areas such as plasma physics,hydrodynamics,fluid mechanics,optics,and quantum electronics.For a better understanding of the tendency of these areas,one usually uses nonlinear partial differential equations (NLPDEs),particulary some interesting models arising from Boussinesq equation (see [28,29]).Many mathematical approaches have been proposed to investigate the exact solitary wave solutions like,unified strategy [1],Painlevé approach [2],Wronskian formulation [3],linear superposition principle [4],Hirota bilinear method[5],inverse scattering method [8],invariant subspaces [9],Nucci’s reduction strategy [10],and symmetry reduction strategy [11].

The GKM is considered as a very convenient strategy to generate the analytical solutions of NLPDEs [16].The fundamental concept was generalized to a so-called transformed rational function strategy [12,13].There are assorted sorts of Kudryashov strategies in the existing literature such as the Kudryashov procedure,extended Kudryashov procedure,and modifed Kudryashov procedure.

The ERFM is straight,simple,and effective to apply where it can be applied to a lot of NLPDEs for seeking exact traveling wave solutions.This procedure is advantageous since it applies to equations with a high balancing number.In other analytical solution procedures,as the balancing number becomes higher,the computational cost increases.

The METFM is an applicable strategy for lots of NLPDEs.With this method,we obtain a much wider solution family than the tanh and the extended tanh methods.

In our work,we are inspired to study essential equations in many physical applications,known as Mikhailov-Novikov-Wang equation (MNWEq),which can be expressed as follows:

This is an integrable equation with a dynamical behavior where by the differential polynomial ring’s extension,a well-known equation in nonlinear science,named Boussinesq equation,belongs to this classification [17,38,39].Therefore,studying this equation can provide a good understanding to many interesting nonlinear scientific phenomena in physics and oceanography.This topic is of current research interests and the results provide an essential tool to understand nonlinear wave phenomena.In general,with the help of the Hirota bilinear method,N-soliton solutions can be systematically studied for both (1+1) -dimensional integrable equations[44] and (2+1) -dimensional integrable equations [45,46].In addition,other novel interesting equations in (2+1) -dimensions have been studied [47,48].

Recently,several research works have been done on investigating various classes of differential equations in the sense of fractional calculus [20,21,30–37] because fractional derivatives can provide a powerful tool for interpreting many physical systems that cannot be interpreted using the integer derivatives.Many systems possess a memory effect,therefore,there is a need for modeling such systems with the help of fractional derivatives.All fractional definitions have both advantages and disadvantages.To overcome the challenges of finding analytical solutions for certain systems modeled in the sense of nonlocal fractional derivatives,conformable derivative [49],type of local fractional derivative,can offer a simple tool to deal with several differential equations,particularly NLPDEs,by solving them analytically [6,7,25] in a very simple way in comparison to the classical fractional derivatives which may require some new and generalized numerical techniques and approximations (see [40–43] for more related applications via conformable definition).Various recent studies have been dedicated to the mathematical analysis of fractional operators and conformable definition including their essential properties [14,15,19,23,26].

While some essential research studies related to ocean engineering and science have been recently conducted such as the investigation of the extended (2+1) -dimensional Boussinesq equation’s exact solutions via by the method of Lie symmetry analysis [50],5th-order nonlinear water wave equation via the The Kudryashov methods [51],complex nonlinear Davey-Stewartson equations via the techniques of extended exponential function and Khater II [52],and (2+1) -dimensional Korteweg-De Vries equation with time-variable coefficients via the techniques of simplified Hirota and long wave [53],our study is unique and novel because the MNWEq is rarely discussed in other previous research students,and according to the best of our knowledge,it is the first time ever this particular equation has been studied using three different techniques which can offer new direction to understanding nonlinear wave phenomena that play an essential role in oceanography and costal engineering due the common relation between integrability and water waves’ phenomena.

Analytical solutions of this equation have been founded via the (G′/G)-expansion’s strategy [18].The motivation of this current work is to generate new analytical solutions to the MNWEq and plot 3D graphs of the solutions.For this purpose,we implement GKM,ERFM,and METFM.Therefore,the physical meaning of the dealt model can be interpreted.

Next,this manuscript is divided into the following remaining sections: In Section 2,the adopted strategies will be presented.Section 3 provides new exact solutions and plots 3D graphs of the dealt model.Finally,we conclude our work in section 4.

2.Methodology

The methodology of three different approaches,namely GKM,ERFM,and METFM will be described respectively in this section.

The following NLPDE is considered:

whereφandPrepresent an unknown function and aφ’s polynomial with its partial derivatives,respectively.Firstly,to solve Eq.(2),a traveling wave transformation (TVS) is used as:

where the speed of the wave is represented byc.From TVS,Eq.(2) is reduced to ODE as:

Here prime denotes derivative w.r.tξ.Eq.(4) should be integrated term by term once or more times.

2.1. The generalized Kudryashov method (GKM)

Conforming to this procedure,the reduced equation’s desired solution is formed byK(ξ)’s polynomial as [16] :

whereai(i=0, 1 ,...,n),bj(j=0, 1 ,...,n) are constants to be determined (aN0,bN0) andK=K(ξ) is the solution of

The solution of Eq.(6) written as:

According to the principle of homogeneous balance (PHB),one can easily verify the positive integerNin Eq.(5) from Eq.(4).Finally,we can obtain a polynomial ofKby subrogating Eq.(5) into Eq.(4) along with Eq.(7).Here,we equate all the coefficients of polynomialKto 0 to obtain an algebraic equation system.This system’s solutions with the assistance of computer software gives the values ofai(i=0, 1 ,...,n),bj(j=0, 1 ,...,n).Finally,one may obtain the soliton-type solutions of the reduced Eq.(4) by substituting these obtained values and Eq.(6) into Eq.(5).

2.2. The exponential rational function method (ERFM)

Step 1.Let us suppose that the Eq.(4) solution can be constructed similarly to some previous studies concerning the analytical solutions to NLPDEs in the context of conformable derivative via the methods of simple equation and ERFM [22],and motivated by a generalized method of ERFM in [24] for solving exactly:

whereaN(aN0) are constants to be found later.Let us determine the integerNby balancing the highest order linear term(HOLT) with the highest order nonlinear term (HONLT) in Eq.(4).

Step 2.Substitution of Eq.(8) into Eq.(4) and collection every single term with the same order ofeiξ(n=0, 1, 2 ,...) together make into the LHS of Eq.(4) another polynomial ineiξ.Then,all coefficients of this polynomial are equated to 0 yielding algebraic equations foranundetermined parameters.Finally,when this equation system is solved,a variety of exact solutions for Eq.(2) is constructed.

2.3. The modified extended tanh-function method (METFM)

We will now deal with METFM to provide all necessary information.The explicit solution of Eq.(4) can be written as:

Here:a0,ai,bi(i=1 ,...,N) are constants which need to be obtained.In addition,aN,bNcan not be zero together namelyaN0 orbN0.Nis the balance term calculated via PHB.In Eq.(9),ψ(ξ) satisfies the Riccati equation in the following form:

Here:bis a constant.The known solutions of the Riccati equation are given as follows:

Hyperbolicsolutions:Ifb<0, the following solutions are given:

Trigonometricsolutions:Ifb>0, the following solutions are given:

Rationalsolution:Ifb=0, the following solution is given:

If we put Eq.(9) and Eq.(10) in Eq.(4),we get a polynomials inψi(ξ). Then,by equating each resulted polynomial’s coefficient to 0,an over-determined set of algebraic equations forb,c,a0,ai,bi(i=1 ,...,N) is obtained.If we solve obtained system via MAPLE software,we get various values ofb,c,a0,ai,bi.Finally we get exact solutions of the given partial differential equation [27].

3.Mathematical analysis

In the current section,some MNWEq’s exact traveling wave solutions are constructed via GKM,ERFM,METFM.

The TVS is used in Eq.(3) for solving Eq.(1).If we apply Eq.(3) to Eq.(1),we obtain following ODE:

Then,by integrating the obtained ODE w.r.tξ, we get: following ODE:

whereJis the constant of integration.Puttingφinstead ofφ′ in Eq.(15),we obtain following ODE:

3.1. Exact solutions via the GKM

Based on the principle of homogeneous balance,one may find thatN=M+2.If we setM=1,we can obtainN=3.Therefore,we can express the solution as:

whereK=K(ξ)is the solution of the Eq.(6).Then,we substitute Eq.(17) into Eq.(16) and utilize Eq.(6).Then,we equate all coefficients of the functionsKkto 0.So,we can obtain the following equation system.Herea0,a1,a2,a3b0,b1andJare the parameters.

The solutions of these algebraic equations have been obtained the help of symbolic computation software: MAPLE.Hence,two cases are given as follows:

Case 1:

Next,by subrogating the acquired values into Eq.(17) with Eq.(7) andφ=φ′,we get the MNWEq’s soliton-type solutions as follows:

whereC1andCare arbitrary constants and

Case 2:

Next,by subrogating the acquired values into Eq.(17) with Eq.(7) andφ=φ′,we get the MNWEq’s soliton-type solutions as follows:

whereC1andCare arbitrary constants and

3.2. Exact solutions via the ERFM

From PHB,the balancing number can be founded asN=2.In this way,we can set the solution as:

By substituting Eq.(20) into the reduced equation Eq.(16) and collecting every single term with the same order ofeiξ(n=0, 1, 2, 3, 4, 5, 6) together,we get a polynomial ofeiξ.Then,we equate each of this polynomial’s coefficient to 0 yielding a set of algebraic equations fora0,a1,a2,candJ.Finally,this system is solved to get a variety of exact solutions for Eq.(1).

Case 1:

Then,subrogation of these values into Eq.(20) gives soliton-type solutions of the MNWEq’s as:

whereCis the integration constant where it is not strictly positive.

By comparing this solution with the one obtained in Eq.(18),we can say that this solution is the same when we setC1=1.

Case 2:

Then,subrogation of these values into Eq.(20) gives soliton-type solutions of the MNWEq’s as:

3.3. Exact solutions via the METFM

By substituting Eq.(9) into the Eq.(16),we get a system.Then,by equating the coefficients ofψj(ξ)(j=0,±1,±2,±3,±4,±5,±6) to 0,we get a system of algebraic equations as:

If we solve above system,we get six cases.

Case 1:

Then,exact solutions are given by in the following form.

Whenb<0,

Whenb>0 ,

Whenb=0, we obtain zero solution andCis the integration constant.

Case 2:

Whenb< 0,

Whenb>0,

Whenb=0, we obtain zero solution andCis the integration constant.

Case 3:

Whenb<0,

Whenb>0,

Whenb=0,

whereCis the integration constant.

Case 4:

Whenb<0,

Whenb>0,

Whenb=0, the same as solution Eq.(29) is obtained andCis the integration constant.

Case 5:

Whenb<0,

Whenb>0,

Whenb=0, the same as solution Eq.(29) is obtained andCis the integration constant.

Case 6:

Whenb<0,

Whenb>0,

Whenb=0, the same as solution Eq.(29) is obtained andCis the integration constant.The 3D graphical representations of some obtained solutions in this study are shown in Fig.1,2,3,4,5,6,7,8 and 9.

Fig.2. The figure of the solution of φ2(x,t) founded in Eq.19 when C1=2, C=0.

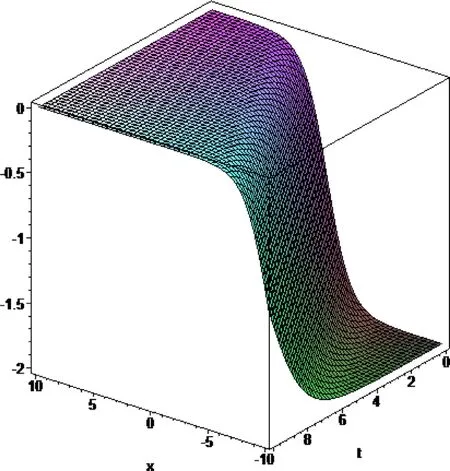
Fig.3. The figure of the solution of φ3(x,t) founded in Eq.21 when C=0.

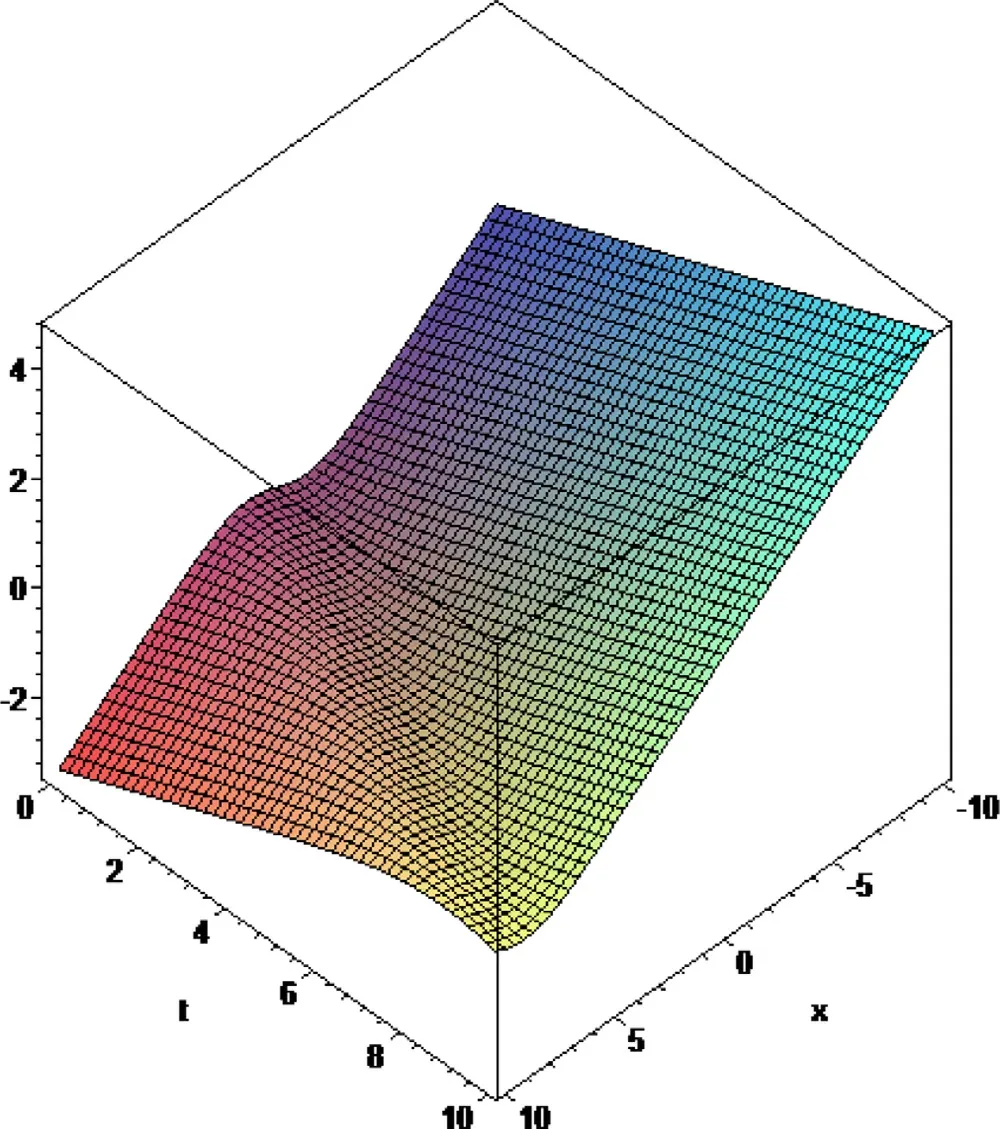
Fig.4. The figure of the solution of φ4(x,t) founded in Eq.22 when C=0.

Fig.5. The figure of the solution of φ5(x,t) founded in Eq.23 when C=0, c=-1.

Fig.6. The figure of the solution of φ6(x,t) founded in Eq.24 when C=0, c=1.

Fig.7. The figure of the solution of φ9(x,t) founded in Eq.27 when C=0, c=-1.

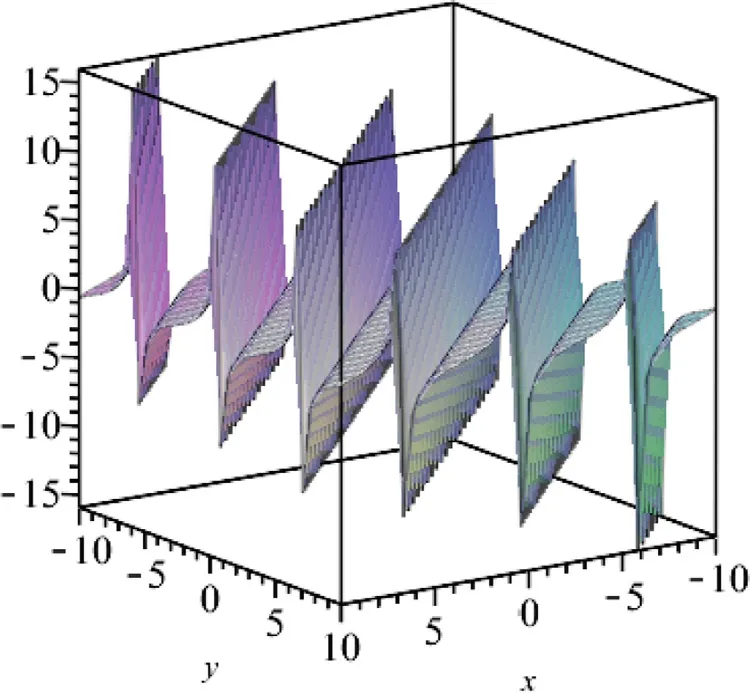
Fig.8. The figure of the solution of φ10(x,t) founded in Eq.28 when C=0, c=1.

Fig.9. The figure of the solution for φ11(x,t) founded in Eq.29 when C=0.

4.Conclusion

Three different approaches,the GKM,ERFM,and METFM have been utilized to procure new soliton-type solutions of MNWEq.Some results are plotted 3D to understand the dynamics of solutions.From our obtained results,our results can be converted to each other by setting the parameters as special values.All our results open a new door to all other researchers to solve many NLPDEs in various oceanographic applications via the three studied techniques.Our results can be further extended to solve various other equations of Boussinesq type due to their importance in understanding several nonlinear phenomena,and the obtained solutions’ stability analysis can be also investigated in future works.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.