基于多尺度加权融合特征学习的转子故障诊断*

王 展,鲁晨琪,星施宇,王卿源

(1.沈阳建筑大学机械工程学院,沈阳 110168;2.沈阳派尔泰科科技有限公司,沈阳 110000)

0 引言

转子系统是高端装备旋转机械的核心部件,其工作状态决定了设备的运行精度和稳定性[1],但转子在工作过程中由于受到工况变化、部件损耗等影响会产生故障,进而降低设备的运行精度甚至导致部件损坏,因此,需要对转子故障进行及时诊断。当前,转子故障诊断主要通过对振动信号进行特征提取的方式诊断故障特征[2],但一维振动信号在时频分析的过程中容易造成高频分量的丢失,导致故障提取不完整,影响诊断精度,而图像作为二维信号,能够更加全面的表达其信号特征[3-4],避免了由于时频分析导致的有用信息丢失,因此将振动信号转化为二维图像,并对图像进行特征提取是转子故障诊断中需要解决的重要问题。

目前,国内外学者已针对二维图像在故障诊断中的应用开展了研究。JHA等[5]将振动信号转化为纹理图像,通过波原子变换提取图像特征,提高了球轴承的故障诊断精度;王明罡等[6]将振动信号的本征模态分量转化成灰度图,利用局部二值模式提取灰度图的纹理特征,实现了轴承的故障诊断;BAI等[7]通过构造频域信号的一阶马尔可夫跃迁矩阵,生成振动信号频谱特征图,通过对特征图进行分类,识别了轮轴箱的复合故障。振动信号通过二维化过程,较完整的保留了故障信息。为了实现准确的故障诊断,还需要对图像特征进行提取并分类。卷积神经网络(CNN)是一种具有模式识别功能的深度学习算法,在图像分类方面有明显优势[8]。HASAN等[9]利用CNN对多域融合图像进行分类,实现了轴承振动状态的识别;TANG等[10]采用贝叶斯算法对CNN模型进行优化,将时频图像作为模型的输入,提高了液压柱塞泵的故障诊断精度;谷玉海等[11]利用CNN对经验模态分解的二值化图像进行分类,实现了滚动轴承的故障诊断。

然而,现有CNN模型大多是使用单一尺寸的卷积核提取图像特征,由于图像特征复杂多样,使用单一尺寸的卷积核容易导致网络模型在特征筛选的过程中遗漏局部重要特征,导致模型的诊断精度不理想。针对这一问题,本文提出一种基于多尺度加权融合特征学习的转子故障诊断方法,通过对称点模式(symmetrized dot pattern,SDP)原理,将振动信号转化为SDP图像,相较于一维信号,更加全面完整的表达故障特征。同时,构建多尺度加权卷积神经网络(multi-scale weighted convolutional neural network,MSW-CNN)模型,利用3个不同的感受野[12]分别提取图像特征,避免单一尺寸的卷积核提取特征时局部特征遗漏的问题,提升模型的分类精度,并通过MSW-CNN模型对SDP图像进行识别,有效提高转子的故障诊断性能。

1 振动信号二维化

对于任意一列振动时序信号X={x1,x2,…,xi,…,xn},其中任意一点xi都可以通过归一化的时间波形映射到极坐标空间中的点S[r(i),θ(i),φ(i)],形成SDP图像[13]。原理如图1所示,其中r(i)为SDP图中点的半径,θ(i)和φ(i)分别为点对应的两个极角,计算过程如式(1)～式(3)所示。

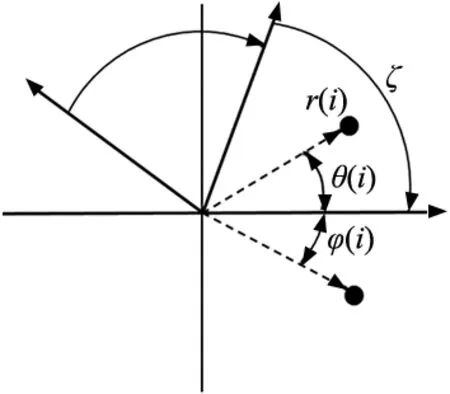
图1 SDP图像原理

(1)

(2)

(3)

式中:xmax和xmin分别为时间序列{x1,x2,…,xi,…,xn}中的最大值和最小值,θ为初始对称轴线的旋转角度,满足θ=360s/n;n为镜像对称平面的个数,s=1,2,3,…,n,l为时间滞后系数,一般取1～10之间的整数;ζ为角增益,满足ζ≤θ。

由式(1)可以得到振动信号的幅值xi的表达式如下:

xi=r(i)×(xmax-xmin)+xmin

(4)

对于一列振动时序信号,其xmax和xmin都是定值,因此幅值xi的大小变化能够由SDP图像中点的半径r(i)表示。

通过对SDP原理变形可以得到表达式如下:

(5)

式中:xi为i时刻的幅值,xi+l为i+l时刻的幅值,xi+l-xi为时序信号中临近点的幅值变化,因此SDP图像可以反映振动频率的变化。

以正弦周期信号x(t)=sin(200πt)为例,采样频率为10 kHz,产生10 000个采样点,设定6个对称镜像平面,即n=6,得到初始对称轴的旋转角度θ=60°,时间滞后系数l取3,角增益ζ为30°,得到的SDP图像如图2所示。

图2 模拟信号的SDP图像

从图中可以看出,振动信号生成的SDP图像可以划分为几个区域,当n=6时,图像可以划分为6个区域,以初始对称轴线的角度60°为起始,生成第一组SDP图形,经过5次镜像对称后得到的SDP图形依次排列,得到图2所示的整体SDP图像,因此,可以通过划分SDP图像的区域,将多组振动信息展现在一张图像上,实现多组振动数据的融合。

在SDP图像中,时序信号的振动特征主要由时间滞后系数l和角增益ζ控制,l一般在1～10之间取值,ζ的取值一般小于初始线的旋转角度,即ζ≤θ,代表SDP图像的绘图区间为[0,θ]。以周期正弦信号x(t)=sin(200πt)为例,在不设定初始称轴和镜面对称的情况下,分别选取ζ=60°,l为2,5,8和l=2,ζ为30°,60°,90°时生成的SDP图像如图3和图4所示。

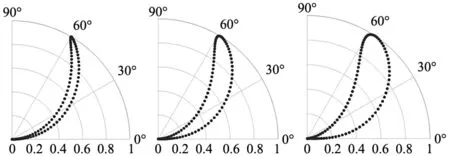
(a) l=2 (b) l=5 (c) l=8

(a) ζ=30° (b) ζ=60° (c) ζ=90°

从图3中可以看出,当ζ=60°时,SDP图像的绘图区间为[0,60°],随着l的增大,图像厚度逐渐增大;从图4中可以看出,当l取固定值时,随着ζ的增大,点的绘图区间逐渐增大,因此能够通过选择适当的l和ζ的值突出SDP图像的特征。

2 多尺度加权卷积神经网络

为了更加全面的提取SDP图像所包含的振动特征,建立一种多尺度加权卷积神经网络(MSW-CNN)模型,模型结构如图5所示。

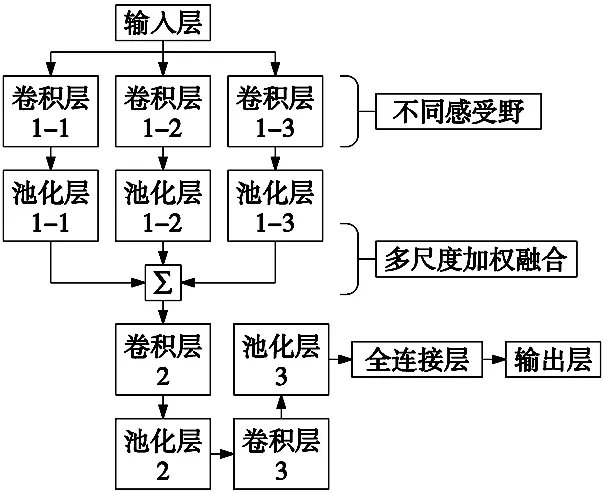
图5 MSW-CNN模型结构

首先,在第一个卷积层通过3个不同尺寸大小的卷积核对图像进行卷积,形成3个卷积通道,不同尺寸的卷积核对应不同大小的感受野,两者关系如下:

rfn-1=(rfn-1)×Sn-1+kn-1

(6)

式中:rfn-1为n-1层感受野大小,kn-1为n-1层卷积核大小。

通过不同的卷积核进行特征提取后,各通道的输出为:

(7)

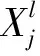
图像经过卷积之后,需要进行池化处理,本文采用最大池化,设移动步长为F,则池化后的输出为:

yi=max(xF×i+j)

(8)

各通道的感受野分别进行特征提取并池化之后,获取相同数量的特征图,因此需要对其进行特征融合,由于各感受野提取到的图像特征的相对重要性存在差异,因此需要对各通道进行权重分配,本文采用峭度值表示3个通道对应的权重值,公式如下:

(9)

式中:aj为通道j的峭度值,kj表示通道j上振动信号的峭度值,m表示通道数。

下一步需要对各通道特征进行融合,融合后的输出特征公式如下:

(10)

经过加权融合后的特征图像能够更有效的突出振动信号的关键特征,再经过两组卷积池化层,输入到全连接层,经过Softmax分类器对图像特征进行分类,实现转子的故障诊断。

3 转子故障诊断实验

3.1 搭建实验平台

为验证所提方法的有效性,本文采用某公司生产的机械故障综合模拟实验台(MFS)进行实验验证。将两个加速度传感器分别安装在转盘左右两侧采集振动信号。实验共采集6种转子状态的振动信号,分别为正常、不对中故障、碰摩故障和不平衡故障,其中不平衡故障分为3种不平衡量,分别为15.6 g·mm、31.2 g·mm和46.8 g·mm。实验中通过改变联轴器上两轴的相对位置来模拟不对中故障,通过固定铜棒和转轴的距离,使其接触摩擦来模拟碰磨故障,通过在转盘边缘半径为39 mm的螺纹孔内旋入质量为0.4 g、0.8 g和1.2 g的螺钉来模拟不平衡故障,实验平台如图6所示。

图6 转子故障模拟实验台

3.2 生成SDP图像

实验中设定2600 r/min、2800 r/min和3000 r/min三种转速,每种转速下每种振动状态采集200组数据,其中100个为训练样本,100个为测试样本,每个样本中包含2048个数据点,数据集描述如表1所示,6种转子状态的振动时域信号如图7所示。

(a) 正常 (b) 不对中

(c) 碰磨 (d) 不平衡量15.6 g·mm

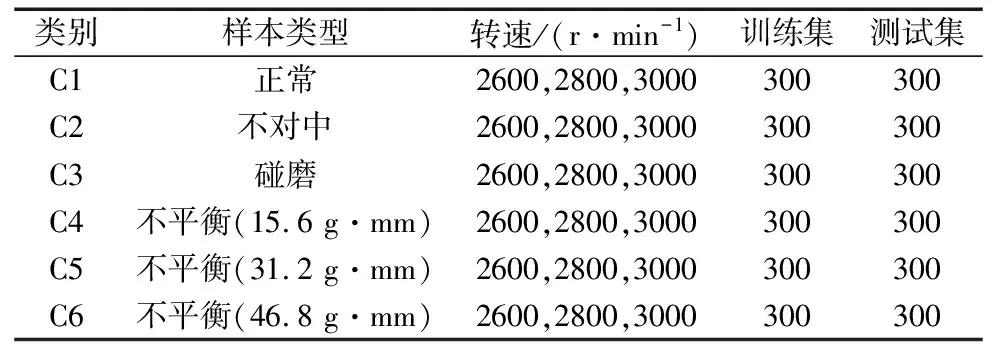
表1 数据集描述

随后,对振动信号进行二维化处理,根据SDP图像的生成原理,将6种转子振动状态的时域振动信号生成对应的SDP图像。为了更加全面的表达不同振动状态下的转子故障特征,根据SDP图像能够同时展现多组振动信息的特点,将传感器1和传感器2采集的振动信号融合在一幅SDP图像上,设定初始对称轴的角度为60°,每个传感器数据生成的SDP图形分别做2次镜面对称,选取时间滞后系数l为3,角增益ζ为30°,以碰磨故障为例,两个传感器数据融合的SDP图像如图8所示。

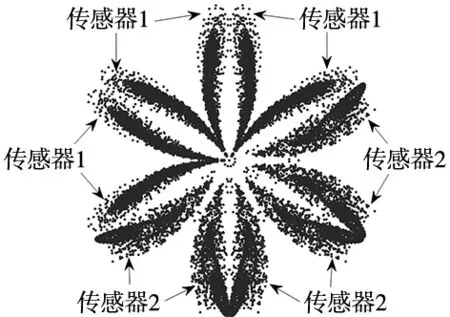
图8 碰磨故障下多传感器数据融合的SDP图像

从图8可以看出,转子振动信号的SDP图像表现为花瓣的形式,并且两个传感器数据生成的SDP图像形状略有差异,与传感器2相比,传感器1对应的花瓣较小,且花瓣中的点较为集中,说明单一传感器采集的数据存在表达振动信息不全面的问题,而使用两个传感器分别在转盘的左右两个不同方向采集数据,得到的振动信息更为全面,有利于提升转子故障诊断的精度。

6种振动状态对应的SDP图像如图9所示。

(a) 正常 (b) 不对中(c) 碰磨

(d) 不平衡量15.6 g·mm (e) 不平衡量31.2 g·mm (f) 不平衡量46.8 g·mm

从图9可以看出,不同振动状态的SDP图像呈现出不同的图像特征。其中,不对中故障对应的花瓣较短,花瓣边缘处仅有零星点的分布;碰磨故障的花瓣边缘处的点分布较为分散;正常状态和不平衡故障的SDP图像整体线条比较相似,但仔细观察可以发现,不平衡故障的花瓣线条较细,并且随着不平衡量的增加,花瓣越来越细,整体线条趋于光滑。因此,通过生成SDP图像,振动故障特征转化为SDP图像的特征,再通过对图像特征进行准确提取并分类,可以有效实现转子的故障诊断。

3.3 模型训练

为了全面的提取SDP图像特征,建立MSW-CNN模型。在模型中,为了充分提取图像信号中的隐含特征,防止局部重要特征遗漏,在第一个卷积层,使用3个不同尺寸大小的卷积核对SDP图像进行卷积,3个卷积核的大小分别为3×3、5×5和7×7,形成3个卷积通道,经过补零后,3个卷积通道输出相同数量的特征图。由于卷积核大小不同,3个卷积通道提取图像细节的能力强弱不同,输出特征的重要性存在差异,因此,对3个通道的输出特征进行加权融合,进一步突出图像的关键特征。经过融合后的图像特征,再经过两组卷积池化层,输入到全连接层,利用Softmax分类器实现特征的分类,进而实现转子故障诊断。MSW-CNN模型的网络参数如表2所示。

表2 MSW-CNN模型参数

将训练集输入到MSW-CNN模型中训练网络,图10显示了MSW-CNN模型在每次迭代中的训练准确率和损失值。从图中可以看出,准确率曲线的上升速度和损失曲线的下降速度都比较快,经过10次训练后,诊断准确率达到97%,迭代20次以后,准确率稳定在98%以上;模型损失值小于0.007,说明所构建模型的分类能力和鲁棒性较好。

(a) 训练准确率曲线 (b) 训练损失曲线

3.4 结果与分析

为了验证本文方法的诊断准确性和稳定性,采用以下3种方法与本文方法进行对比实验,3种方法包括:VGG方法,将振动信号转化成SDP图像,利用VGG-16模型[14]提取图像特征并识别;GWO-SVM模型,利用多尺度均值排列熵表征振动故障特征,采用灰狼优化支持向量机(GWO-SVM)对振动特征进行分类识别[15];MSDI结合随机森林方法:对振动信号进行变分模态分解,构造6类多尺度无量纲指标(MSDI)作为故障振动特征,应用随机森林模型对振动特征进行分类[16]。

在实际应用中,转子故障常伴随噪声出现,因此,为对比几种方法的噪声鲁棒性,在各组振动数据中加入信噪比为15 dB的高斯白噪声,记录加噪声前和加噪声后的实验准确率,每种方法在加入噪声前后分别进行10次随机实验,每次实验的准确率如图11所示,4种方法的平均准确率如表3所示。

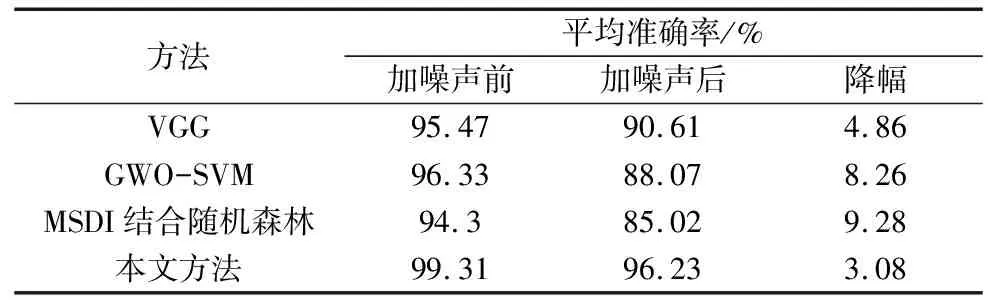
表3 4种方法的平均准确率

(a) 加噪声前随机实验准确率 (b) 加噪声后随机实验准确率

从表3可以看出,加入噪声前,4种方法的平均准确率均高于90%,其中本文方法的准确率最高,为99.31%,比VGG方法高3.84%,说明经过多尺度加权融合后的特征图像能够更有效的突出振动信号的故障特征,在转子故障诊断中更有优势;加入噪声后,4种方法的准确率都有不同程度降低,其中本文方法的准确率为96.23%,高于其他3种方法,并且本文方法的降幅最小,为3.08%,其次是VGG方法,降幅为4.86%,说明SDP图像受噪声影响较小,具有较强的噪声鲁棒性。从图11可以看出,加入噪声前后,本文方法的准确率折线较为平稳,说明本文方法的诊断稳定性强,优于其他3种方法。

图12为本文方法的混淆矩阵,由图可知,加入噪声前,6种振动状态的诊断准确率均高于98%,其中,正常、不对中故障和碰磨故障的准确率为100%,3种不平衡量的平均诊断准确率为98.63%;加入信噪比为15 dB的高斯白噪声后,每种状态的诊断准确率均高于94%,平均准确率达到96.23%,证明所提方法能够有效对转子故障类型进行诊断且具有较好的抗噪性能。

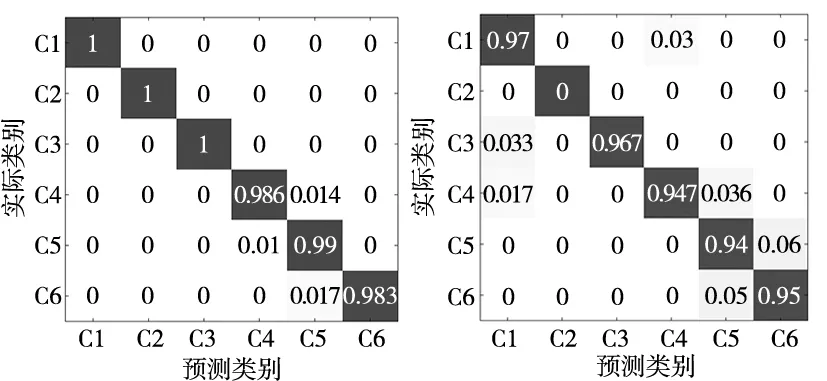
(a) 加噪声前混淆矩阵(b) 加噪声后混淆矩阵

4 结论

本文提出一种基于多尺度加权融合特征学习的转子故障诊断方法,首先对振动信号进行标准化处理,通过选取适当的时间滞后系数和角增益,将多传感器采集的一维振动信号融合为二维的SDP图像;其次,构建了MSW-CNN模型,利用3个不同感受野分别提取图像特征,通过对多通道图像特征进行加权融合提高了模型的分类精度;最后进行了转子故障诊断实验,实验结果表明:

(1)SDP图像能够较完整的表达转子振动故障特征,避免了故障信号中高频分量的丢失,并且受噪声影响小,在信噪比较低的旋转机械振动故障诊断中具有明显优势。

(2)与单尺度的分类器相比,MSW-CNN模型可以通过多尺度加权融合过程更全面的提取图像特征,诊断准确率更高。

(3)本文提出的基于多尺度加权融合特征学习的故障诊断方法,在转子多故障诊断中表现出了较高的精度,且该方法的诊断稳定性强,噪声鲁棒性较好,为旋转机械的故障诊断提供了新思路。