抑制磨削振纹的多目标磨削工艺参数优化
2023-11-28李国龙朱国华蒋林陶一杰贾亚超
李国龙 朱国华 蒋林 陶一杰 贾亚超
摘要:针对蜗杆砂轮磨削齿轮经常出现振纹的问题,采用某型新能源汽车用斜齿轮,通过正交设计实验的方法,探究了磨削工艺参数(砂轮线速度、砂轮轴向进给速度、砂轮径向进给量)对加工振动和齿面粗糙度的影响。采用多元二次回归的方法建立了以减小振动和齿面粗糙度为目标的多目标优化数学模型,采用遗传算法优化了磨削工艺参数。结果表明,优化后的工艺参数可在保持稳定的齿面粗糙度精度的同时大大削弱磨削中的振动,有效防止了振纹的产生,延长了机床的使用寿命。
关键词:振纹;蜗杆砂轮磨;齿面粗糙度;工艺参数优化;新能源车用齿轮
中图分类号:TH16
DOI:10.3969/j.issn.1004-132X.2023.09.009
Optimization of Multi-objective Grinding Process Parameters to Suppress Chatter Marks
LI Guolong ZHU Guohua JIANG Lin TAO Yijie JIA Yachao
Abstract: Aiming at the problems of chatter marks frequently occurring in gear grinding with worm-shaped grinding wheel, the effects of grinding process parameters (linear speed of grinding wheel, axial feed speed of abrasive wheel, radial feed of grinding wheel) on machining vibrations and tooth surface roughness were investigated by orthogonal design experiments of helical gears used in a certain type of new energy vehicles. A multi-objective optimization mathematical model was established with multiple quadratic regression method to reduce vibrations and tooth surface roughness, and genetic algorithm was used to optimize grinding parameters. The results show that the optimized processing parameters may greatly reduce the vibrations in grinding while maintaining the stable roughness value of tooth surfaces, effectively prevent the generation of chatter marks and prolong the working life of the machine tools.
Key words: chatter mark; worm-shoped grinding wheel; tooth surface roughness; processing parameter optimization; gear for new energy vehicles
0 引言
在蜗杆砂轮磨削出的齿轮表面经常会出现明暗条纹状的周期性规律纹路,此纹路触摸起来凹凸不平,通常这种纹路被认为是磨削加工过程中振动过大而形成的,所以被称为振纹。齿面振纹的存在会使齿轮啮合时载荷无法平稳传递而产生振动,因此有振纹的齿轮工作中会经常出现啸叫等噪声[1],此啸叫噪声在新能源汽车高速高扭矩状态下尤为明显,因为新能源汽车不存在内燃发动机声音的遮盖,会使零部件噪声更加突出。作为汽车传动系统重要部件,齿轮的质量对提高车辆NVH性能和改善乘坐舒适性有重要意义[2]。这种振纹还会严重影响齿面的接触质量,齿轮不正确啮合会使齿面局部过载,局部齿面严重磨损,使用寿命缩短,甚至造成轮齿断裂。
磨床在加工过程中振动过大会降低各磨床部件的使用寿命,如主轴振动过大会使轴承的受力不均匀,进而导致应力集中且降低其使用寿命,磨床振动的同时还会产生噪声污染,加工出的工件表面质量也会进一步下降[3-4]。作为齿轮加工的最后一道工序,磨齿对齿轮的表面形貌具有重大影响。作为评价齿面质量的重要指标之一,齿面粗糙度对齿轮的接触疲劳、耐磨性和传动质量均有重要影响[5]。
蜗杆砂轮磨齿因为高效率、低成本、磨削性能与质量稳定等优点,目前被大量应用于中小模数齿轮的磨削加工中[6],故新能源汽车小模数齿轮多采用此方法加工。但是蜗杆砂轮磨削加工后的齿轮表面微观质量却时常出现不合格的情况,特别是不合理的磨齿工艺参数设置容易在齿轮表面产生振纹或者粗糙度不达标。可通过工艺参数优化来实现加工目标,关于工艺参数优化模型的建立与求解方法,陈鹏等[7]以自动化加工效率、齿轮单件成本为目标,工件材料、刀具涂层及切削速度、进给量等因素为变量,建立了一种齿轮高速干式滚切工艺参数优化模型。曹卫东等[8]针对少量历史加工案例支撑下的工艺参数优化问题,提出一种融合支持向量回归和多目标蜻蜓算法的高速滚齿工艺参数优化方法。李聪波等[9]以不同刀具磨损状态下的工艺参数为优化变量,建立了考虑刀具磨损的数控车削批量加工工艺参数节能优化模型,并采用多目标模拟退火算法进行优化求解。WU等[10]建立了效率-成本-精度三目标模型的寻优问题,提出了一种具有自适应进化参数的多目标融合进化算法。KHARKA等[11]采用神经网络与实数编码遗传算法对齿轮制造工艺进行参数优化,以同时最小化微几何偏差和表面粗糙度。SHARMA等[12]采用可取性函数分析方法對刀具侧面磨损和表面粗糙度进行并行优化,得到了多响应的最优参数组合。
现有研究缺乏工艺参数对磨齿加工中振动的影响的探索与实验。本文以蜗杆砂轮磨削某型新能源车用斜齿轮为实验基础,采用正交设计实验方案,探究了磨齿加工中不同工艺参数对磨齿加工中振动大小以及齿轮表面粗糙度的影响。然后基于实验数据建立了工艺参数与振动、粗糙度的回归预测模型,分析了各个参数对振动和粗糙度的影响及原因。最后构建以同时减小加工振动、齿面粗糙度为目标的多目标优化模型,采用遗传算法对加工参数优化,得到了加工振动小、粗糙度小的工艺参数。
1 磨削实验设计
1.1 实验
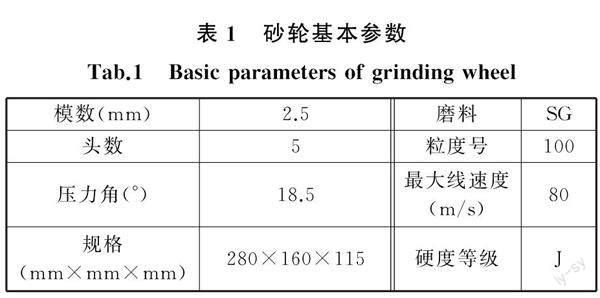
本实验在中国重庆机床有限责任公司生产的YW7232CNC型数控蜗杆砂轮磨齿机上进行,磨削砂轮为郑州宏拓精密工具有限责任公司生产的蜗杆磨CA砂轮,砂轮的磨料是SG磨料和白刚玉辅料,其中SG磨料占50%,其余是辅料;砂轮其他基本参数见表1。实验齿轮为某型新能源车用斜齿轮,材料为20CrMnTiH,斜齿轮基本参数见表2,材料力学性能见表3。
信号采集设备有PCB品牌振动加速度传感352C34、PC信号调理器480C02、PCB低噪声线缆2003D20、HIOKI品牌信号采集记录仪8861-50。现场实验设备布置安装与信号采集设备如图1所示。
1.2 实验方法设计
对表面质量影响较大的因素有磨削工艺参数(砂轮线速度、砂轮轴向进速度、砂轮径向进给量)、磨削加工运动轨迹、砂轮特性与形貌、砂轮是否磨损与修整、磨削液、工件材料、工艺系统的刚度及其动态特性等[13]。磨齿作为本斜齿轮加工的最后一道加工工序,工艺参数设置的重点是要保证斜齿轮的表面加工质量。根据控制变量原则,在机床、冷却润滑液、加工工件、砂轮等条件不变的情况下变更工艺参数,采用三因素三水平的正交设计实验方法探究工艺参数对斜齿轮表面质量和加工中振动的影响。根据此型号斜齿轮实际加工中推荐的磨削参数范围获得实验组表格,见表4。
振动信号设备设置振动采样频率为10 kHz,在YW7232CNC数控磨齿机上根据表4中不同组的工艺参数设置对斜齿轮进行磨削,在每一件斜齿轮开始精加工后按下信号存储记录仪8861-50上的开始按钮采集振动信号。采用KEYENCE超景深三维立体显微镜VHX系列测量加工好的齿轮齿面粗糙度。
2 振动粗糙度结果分析与模型的建立
2.1 实验数据处理与分析
采集到的振动加速度信号如图2所示。在振动信号采集过程中发现磨齿精加工过程中的振动远远大于滚齿粗加工时的振动。对测得的磨齿振动数据进行分析处理,选取均方根值(root mean square,RMS)作为特征值进行振动分析,振动均方根值的物理意义是振动信号的平均强度大小,RMS值按照下式计算:
(1)
式中,xi为分析采样数据;n为分析采样数据个数。
表面粗糙度是加工去除材料时零件表面产生的不平整度,主要的评定参数有轮廓算数平均偏差 Ra、轮廓最大高度Ry等。因为Ra的概念更为直观,能够全面地表征零件加工表面微小峰谷的高低以及细密程度,是国内外使用最广泛的表面粗糙度评定参数,故本文采用Ra对磨削表面粗糙度进行评估。
按照表4的正交设计方案完成9组实验,并按照上述方法对测得的数据进行处理,得到每组实验的齿面粗糙度和振动均方根值,详细数据见表5。
2.2 振动模型的建立
2.2.1 振动均方根值回归方程
用得到的振动均方根值与工艺参数值进行多元二次回归,得到振动回归模型方程如下:
f1=17.354 333-0.856 028x1+0.088 744x2+0.010 522x21-0.000 172x22-0.000 345x1x2+0.366 111x1x3-0.134 11x2x3(2)
式中,f1为振动均方根值;x1、x2、x3分别为砂轮线速度、砂轮沿齿轮轴向进给速度和径向进给量。
表6中,对比振动模型预测的振动均方根值与实际测得的振动均方根值,模型预测的数值十分接近实际测得的值。
决定系数R2(coefficient of determination)是反映模型拟合优度的重要统计量,常用于评价回归模型优劣程度。R2的取值范围为0~1。R2的值越大,越接近1,说明回归模型对真实值的拟合程度越好;反之,R2的值越小,说明回归模型对真实值的拟合程度越差。本振动回归模型的决定系数R2=0.999 75,可见此回归模型拟合效果十分理想。
2.2.2 工艺参数单因素对振动的影响
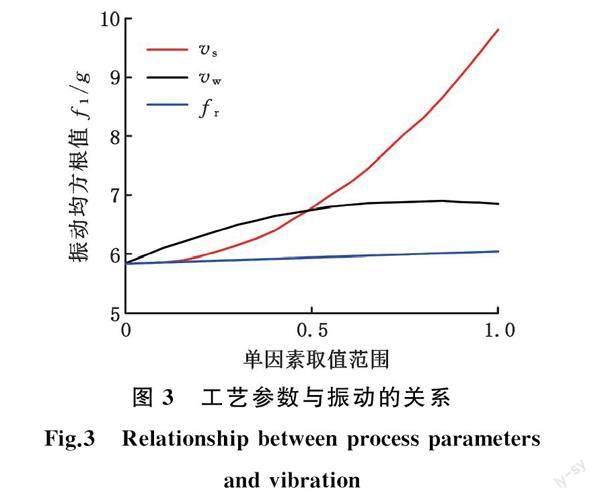
将3个工艺参数自变量范围都进行归一化处理,得到3个工艺参数单因素与因变量振动均方根值之间的关系,如图3所示。
由图3知,振动均方根值随着砂轮线速度的增大而快速增大,成正相关。在砂轮线速度从40 m/s变化到60 m/s的过程中,振动均方根的值从5.84g变化为9.81g,砂轮线速度在3个加工参数因素之中對振动的影响最大、最明显。原因是砂轮制造过程中磨粒分布的不均匀、气孔的存在以及磨削加工过程中的磨损造成表面不均匀和切削液的附加等因素,在砂轮旋转的过程中会产生一个动不平衡量,砂轮在高转速下的动不平衡会更加明显,砂轮及其轴系高转速下的动不平衡是产生磨床振动的最主要来源[14]。滚齿的转速范围通常在500~1000 r/min,振动加速度范围通常在-10g~10g。磨齿的转速范围通常在2000~6000 r/min,振动加速度范围通常在-40g~40g,因此,磨齿的振动比滚齿的振动明显大很多。
砂轮轴向进给速度与振动均方根值关系也成正相关,但是随着轴向进给速度的增大,振动均方根值的增速变慢,到达最大值后数值平稳波动。在砂轮轴向进给速度从100 mm/min变化到200 mm/min的过程中,振动均方根的值从5.84g变化为6.85g,轴向进给速度在三个加工参数因素中对振动的影响仅次于砂轮线速度。这是由于砂轮轴向进给速度过大会造成加工工件及机床刀具主轴和工件装夹芯轴等部件刚度和稳定性不足,从而产生振动。
砂轮径向进给量对振动均方根值的影响最小,在砂轮径向进给量从0.01 mm变化到0.22 mm的过程中,振动均方根的值仅仅从5.84g增加到6.04g,对振动大小几乎不产生影响。
2.3 粗糙度模型的建立
2.3.1 粗糙度回归模型
同理,用齿面粗糙度值与工艺参数进行多元二次回归,得到粗糙度回归模型方程如下:
f2=2.285 039-0.058 481x1+0.003 988x2+0.000 437x21+0.667 476x23-0.000 054x1x2(3)
式中,f2为粗糙度值。
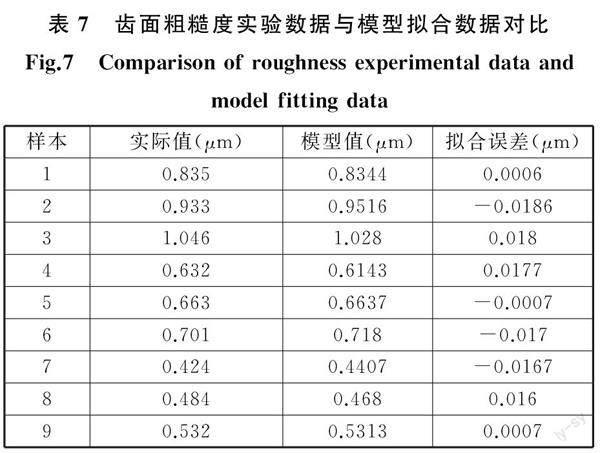
对比粗糙度模型预测的粗糙度值与实际测得的粗糙度值,模型预测的数值十分接近实际测得的值,且决定系数R2=0.994 82。对比结果如表7所示。
2.3.2 工艺参数单因素对粗糙度的影响
同样归一化后,得到3个工艺参数单因素与粗糙度之间的关系,如图4所示。可见粗糙度值随着砂轮线速度的增大而减小,在砂轮线速度从40 m/s变化到60 m/s的过程中,粗糙度值从0.85 μm减小到0.43 μm,这是因为砂轮线速度的增加会使单位时间内通过磨削区的磨粒数量变多,单颗磨粒未变形切屑厚度减小且工件表面上切痕深度变浅,有利于切屑的形成,缩短了磨粒切刃的单次磨削时间,降低了磨粒去除材料后在加工表面留下的隆起高度,最终导致齿面粗糙度减小[15]。
粗糙度值随着轴向进给速度的增大而增大。这是由于轴向进给速度的增加会导致单位时间内磨削齿面的有效磨粒数目减少,使得单位面积齿面上形成的磨削残留高度增大,由此齿面粗糙度值增大[16]。
粗糙度值随着砂轮径向进给量的增大而增大。这是因为径向进给量的增加会使单颗磨粒的最大磨削厚度增大,磨削力也增大,导致磨削表面变形程度增加,由塑性变形引起的凸起高度增大,齿面粗糙度值也会增加。但径向进给量的改变对齿面粗糙度的影响与其他两个工艺参数相比并不是很明显,这是因为在实际磨削过程中磨削用量是缓慢分次进给的,不是一次以径向进给量进行磨削[17]。
3 综合振动与粗糙度优化模型的建立与求解
3.1 遗传算法原理
遗传算法[18](genetic algorithm, GA)的是模拟生物进化过程的自然选择和遗传学机理计算模型,是以一种群体中的所有个体为对象,并利用随机化技术指导对一个被编码的参数空间进行高效搜索最优解的方法。遗传算法的基本运算过程如下。
(1)初始化。设置进化代数计数器t←0,最大遗传代数T,随机生成N个个体作为初始群体G(0)。
(2)个体评价。计算群体G(t)中各个个体的适应度,适应度是用来判断群体中的个体的优劣程度的指标,是根据目标函数来进行评估的。
(3)选择运算。群体进行选择运算,目的是将优化的个体遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。
(4)交叉运算。群体进行交叉运算,是指将两个父代个体的部分结构替换重组而生成新个体。交叉使遗传算法的搜索能力大大提高,在遗传算法中起核心作用。
(5)变异运算。群体进行变异运算,对个体串的某些基因座上的基因值作变动。变异运算可以使遗传算法具有局部随机搜索能力,加速了向最优解收敛的速度,维持了群体的多样性,防止了未成熟收敛现象的出现。
(6)群体G(t)经过选择、交叉、变异运算之后得到下一代群体G(t+1)。
(7)终止条件判断。若t=T,则以进化过程中所得到的具有最大适应度个体作为最优解输出,终止计算。
遗传优化算法流程如图5所示。
3.2 优化模型的建立
为保证在使用蜗杆砂轮磨齿机加工新能源汽车用斜齿轮时不产生振纹,需要在齿轮表面粗糙度满足加工要求的前提下尽可能地减小振动。根据此特点要求进行多目标工艺参数优化,为将二维多目标问题降低为一维优化问题,采用线性加权和法的评价函数方法,按各目标的重要程度赋予其相对应的权系数,然后对其进行线性组合并进行最小值寻优:
(4)
式中,W1、W2分别为振动与粗糙度对应的权重系数, W1,W2∈(0,1),且W1+W2=1。
为了使数据处理更加方便,需要对目标进行归一化处理,将数据映射到0~1范围之内,本文采用线性归一化,线性归一化表达式为
(5)
则本文优化目标表达式变化为
(6)
约束条件如下:
(1)砂轮线速度约束。为防止砂轮加工时破裂,保障加工过程中的安全性,砂轮线速度不能超过砂轮上标识的最大安全使用速度;同时为保证齿轮表面的粗糙度符合使用要求,参考本齿轮现场实际生产参数設置经验,砂轮线速度不能设置过低。因此,砂轮线速度的取值范围设置为35 m/s≤vs≤70 m/s。
(2)砂轮轴向进给速度约束。轴向进给速度越小,加工齿轮的时间越长,为保证较高的齿轮磨削效率,轴向进给速度不能设置过低。为防止砂轮磨损速率过快、齿轮表面质量下降,轴向进给速度也不能设置过高。因此,砂轮轴向进给速度的取值范围设置为75 mm/min≤vw≤225 mm/min。
(3)砂轮径向进给量约束。磨削热随着径向进给的增大而增大,为防止产生的大量磨削热烧伤齿面表面[19],同时考虑到加工次数与效率,砂轮径向进给量取值范围设置为0.04 mm≤fr≤0.28 mm。
综上,联立优化目标函数与约束条件,建立了以减小齿轮加工过程中振动大小、同时提高磨齿表面加工质量为目标的多目标优化模型:
(7)
式中,f1max、f1min分别为振动均方根值的最大值和最小值;f2max、f2min分别为粗糙度值的最大值和最小值。
3.3 优化结果
遗传优化算法的参数设置:种群大小100,最大遗传代数120,交叉概率0.7,变异概率0.02;考虑加工振动与齿轮表面粗糙度,选择振动权重系数W1=0.4、粗糙度权重系数W2=0.6进行优化求解,进化过程如图 6所示。
现有实际加工参数结果和优化后参数加工结果的对比见表8。可知,使用同时考虑振动与粗糙度的优化后参数加工时相比实际加工时振动均方根值减小了3.772g,优化率高达35.81%;加工后齿轮齿面粗糙度降低了0.017 μm,优化率为3.51%。综上所述,本文方法可以在保持稳定的粗糙度精度的同时,大大减小了振动,从而有效防止振纹的产生,提高了机床的使用寿命。
4 结论
(1)针对蜗杆砂轮磨齿机加工新能源汽车斜齿轮时出现振纹的问题,通过正交设计实验建立了加工振动及齿面粗糙度预测模型,并通过与实验数据比较,证明两种模型拟合效果良好。
(2)由两模型可得,振动的大小随着砂轮线速度的增大而快速增大,隨着轴向进给速度的增大而增大。径向进给量对振动大小的影响较小。齿面粗糙度值随着砂轮线速度的增大而减小,随着轴向进给速度与径向进给量的增大而增大。
(3)建立了以最小振动和最小粗糙度值为加工目标的优化数学模型,与优化前相比,用优化后的工艺参数加工可减小35.81%的振动,粗糙度优化率为3.51%。本文方法可有效防止振纹的产生,提高了机床的使用寿命。
参考文献:
[1]刘祖飞. 基于齿轮修形的变速器啸叫治理[D].长春:吉林大学, 2017.
LIU Zufei. Control of Automotive Gearbox Whine Based on Gear Tooth Modification[D]. Changchun:Jilin University, 2017.
[2]黎志鹏. 某纯电动客车振动噪声试验与性能优化研究[D].长沙:湖南大学, 2018.
LI Zhipeng. Research on Vibration and Noise Experiment and Performance Optimization of the Pure Electric Bus[D]. Changsha:Hunan University, 2018.
[3]薛兵. 磨床砂轮动平衡仪控制系统设计及关键技术[D].郑州:郑州大学, 2017.
XUE Bing. Control System Design and Key Technology of Grinding Wheel Dynamic Balancer[D]. Zhengzhou:Zhengzhou University, 2017.
[4]付豫龙. 基于PLC的砂轮动平衡系统研究[D].杭州:浙江大学, 2015.
FU Yulong. Research on Dynamic Balance System of Grinding Wheel Based on PLC[D]. Hangzhou:Zhejiang University, 2015.
[5]MING Xingzu, GAO Qin, YAN Hongzhi, et al. Mathematical Modeling and Machining Parameter Optimization for the Surface Roughness of Face Gear Grinding[J]. International Journal of Advanced Manufacturing Technology, 2017, 90(9):2453-2460.
[6]周泓曲. 改善齿轮表面纹理的蜗杆砂轮磨削方法研究[D].重庆:重庆大学, 2016.
ZHOU Hongqu. Research on Grinding Method of Worm Grinding Wheel to Improve Gear Surface Texture[D]. Chongqing:Chongqing University, 2016.
[7]陈鹏,曹华军,张应,等. 齿轮高速干式滚切工艺参数优化模型及应用系统开发[J]. 机械工程学报, 2017, 53(1):190-197.
CHEN Peng, CAO Huajun, ZHANG Ying, et al.Optimization Model and Application System Development of Gear High-speed Dry Hobbing Process Parameters[J]. Journal of Mechanical Engineering, 2017, 53(1):190-197.
[8]曹卫东,阎春平,吴电建. 支持少样本的高速滚齿工艺参数优化[J]. 计算机集成制造系统, 2018, 24(10):2502-2513.
CAO Weidong, YAN Chunping, WU Dianjian. Optimization of Cutting Parameters for High-speed Gear Hobbing Based on Small Sample Problem[J]. Computer Integrated Manufacturing Systems, 2018, 24(10):2502-2513.
[9]李聪波,余必胜,肖溱鸽,等. 考虑刀具磨损的数控车削批量加工工艺参数节能优化方法[J]. 机械工程学报, 2021, 57(1):217-229.
LI Congbo, YU Bicheng,XIAO Qinge, et al. An Energy-saving Optimization Method for Numerical Control Turning Batch Processing Parameters Considering Tool Wear[J]. Journal of Mechanical Engineering, 2021, 57(1):217-229.
[10]WU Dayuan, YAN Ping, GUO You, et al. Integrated Optimization Method for Helical Gear Hobbing Parameters Considering Machining Efficiency, Cost and Precision[J]. International Journal of Advanced Manufacturing Technology, 2021, 113(3):735-756.
[11]KHARKA V, JAIN N K, GUPTA K. Predictive Modelling and Parametric Optimization of Minimum Quantity Lubrication-assisted Hobbing Process[J]. International Journal of Advanced Manufacturing Technology, 2020, 109(5):1681-1694.
[12]SHARMA V K, RANA M,SINGH T, et al. Multi-response Optimization of Process Parameters Using Desirability Function Analysis during Machining of EN31 Steel under Different Machining Environments[J]. Materials Today:Proceedings, 2021, 44:3121-3126.
[13]明興祖,罗旦,刘金华,等. 面齿轮磨削加工工艺参数的优化[J]. 中国机械工程, 2016,27(19):2569-2574.
MING Xingzu, LUO Dan, LIU Jinhua, et al.Stu-dy on Grinding Process Parameters of Face Gear[J]. China Mechanical Engineering, 2016,27(19):2569-2574.
[14]杨苏. 砂轮振动信号提取及动平衡控制装置研制[D].长春:长春工业大学, 2016.
YANG Su.Research on Grinding Wheel Vibration Signal Extraction and Dynamic Balance Control Device[D]. Changchun: Changchun University of Technology, 2016.
[15]尹国强. 新型CBN高速点磨削砂轮磨削性能研究[D].沈阳:东北大学, 2016.
YIN Guoqiang.Research on Grinding Performance of New CBN High Speed Point Grinding Wheel[D]. Shenyang:Northeastern University, 2016.
[16]闫江波. 新型点磨削砂轮磨削性能实验研究[D].沈阳:东北大学, 2014.
YAN Jiangbo. Experimental Research on Grinding Performance of a New Point Grinding Wheel[D]. Shenyang:Northeastern University, 2014.
[17]徐兰英,伍强,何宝兰,等. RV减速器摆线齿轮磨削表面粗糙度试验研究[J]. 机床与液压, 2020, 48(20):49-53.
XU Lanying, WU Qiang, HE Baolan, et al.Experimental Study on Grinding Surface Roughness of Cycloid Gear of RV Reducer[J]. Machine Tool & Hydraulics, 2020, 48(20):49-53.
[18]任平. 遗传算法(综述)[J]. 工程数学学报, 1999(1):3-10.
REN Ping. Genetic Algorithms(Review)[J]. Journal of Engineering Mathematics, 1999(1):3-10.
[19]王利亭,赵秀栩,李娇. 蜗杆砂轮磨齿加工参数优化[J]. 中国机械工程, 2021, 32(17):2136-2141.
WANG Liting, ZHAO Xiuxu, LI Jiao.Grinding Parameters Optimization of Worm Grinding Wheel[J]. China Mechanical Engineering, 2021, 32(17):2136-2141.
(编辑 陈 勇)
作者简介:
李国龙,男,1968年生,教授、博士研究生导师。研究方向为智能制造技术与系统、复杂零件数字化制系统与装备、精密/超精密加工技术。E-mail:glli@cqu.edu.cn。
收稿日期:2022-05-25
基金项目:国家重点研发计划(2019YFB1703700)
