伺服系统机械谐振的在线检测及其抑制*

袁 铖,李翔龙,杨 铭,陈 兵

(1.四川大学a.机械工程学院;b.创新方法与创新设计四川省重点实验室,成都 610065;2.东方电气股份有限公司,德阳 618000)

0 引言

伺服控制系统广泛运用于工业生产当中,如自动化生产线、工业机器人以及数控机床。这些系统大多都具有丝杆、齿轮、皮带、联轴器、传动轴等传动部件。由于这些机械部件具有一定的柔性,在控制系统高增益的情况下可能会发生机械谐振,具体表现为电机转速在给定值附近发生严重震荡,产生噪声,恶化电机定位精度,严重的会导致机械运动部件的损坏。因此机械谐振的检测与抑制在电机伺服控制中十分重要。

学者们针对伺服系统机械谐振问题提出了许多解决方案。常用的PI参数整定法整定过程复杂[1-3],伺服系统性能难以通过调节PI参数得到提高;构造扰动观测器可以将信号的谐振成分以补偿的形式消除[4-6],但观测器的参数只能离线设置,并且需要较精确的伺服机械参数;陷波器可以有效抑制机械谐振[7],但需要知道当前伺服系统谐振频率。YANG等[8]通过带通滤波器跟踪共振频率,再设置陷波器抑制谐振;康逸儒等[9]采用SDFT检测共振频率,以此设置陷波器参数,抑制舒速度相比传统FFT方法获得了较大的提升,但整定陷波器参数需要伺服系统机械参数。

本文提出一种基于SDFT的伺服系统机械谐振检测方案,优化了SDFT的计算,可以快速的检测出电机转速中的谐振成分,设计出一套自动设定陷波器参数的整定规则,使伺服系统可以在线辨识机械谐振并完成陷波器参数整定,达到机械谐振抑制的目的。

1 伺服系统机械谐振成因

伺服电机通常需要使用联轴器、丝杆、皮带等柔性连接件连接到负载。将连接件的转动惯量合并到负载惯量中,把连接件视为扭转弹簧,建立如图1所示的双惯量模型。

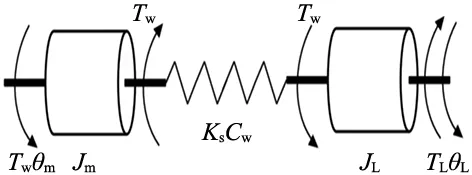
图1 双惯量系统模型

电机根据转矩电流大小输出电磁转矩,电磁转矩使连接件发生扭转将转矩传递到负载。为便于分析,忽略传动间隙建立如下的双惯量系统动力学模型:

(1)

式中:Tm、TL、Tw分别为电磁转矩、负载侧转矩和传动部件转矩,θm、θL为电机侧和负载侧转过的角度,Ks、Cw为传动部件等效的扭转弹簧的刚度和粘滞阻尼系数。

式(1)经拉氏变换整理后得到电机电磁转矩到电机转速的传递函数如下:

(2)

式中:

(3)

可以看出式(2)的等式右边后半部分引入了一个二阶振荡环节,在此二阶振荡环节的作用下会给原有的伺服控制系统带来一个谐振点ωn和一个反谐振点ωa。当伺服系统开环穿越频率处于此谐振点附近时,提高控制器增益会导致系统的幅值裕度小于0 dB,系统不稳定并发生谐振,如图2所示。

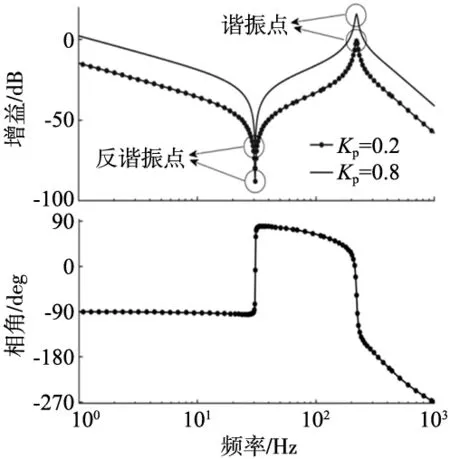
图2 不同增益的控制系统伯德图

2 自适应陷波器设计

陷波器是一种阻带范围较窄的带阻滤波器,它可以将某一频率的信号幅值衰减到给定值以下同时不影响其他频率信号的传递。常用的三参数陷波器传递函数如式(4)所示。

(4)

式中:ω0为陷波器中心频率,ε1为陷波器深度参数,决定中心频率信号的衰减大小,当ε1=0时,陷波器退化为传统的无限深度陷波器;ε2为陷波器宽度参数,决定陷波器阻带范围大小。为了方便后续的代码编写以及陷波器参数的整定,这里将陷波器传递函数的三参数具象化为表征陷波器特征的3个参数,陷波器C语言函数的编写也将采用这3个参数,如图3所示,分别为fnotch、wide、depth。以上三参数按式(5)与传递函数的三参数进行转换:

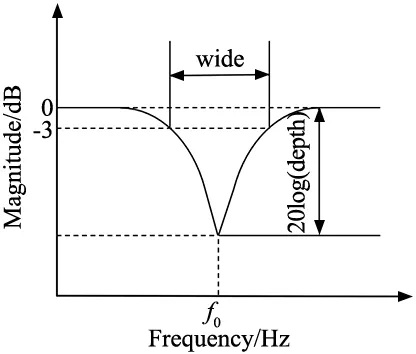
图3 陷波器参数

(5)

2.1 陷波器参数的整定

在充分抑制机械谐振的同时不能降低伺服系统的稳定性,需要合理的整定陷波器的3个参数。

陷波器的阻带范围较窄,因此陷波器的陷波频率应当可以良好的跟踪机械谐振的频率,若误差过大则不能滤除谐振信号;陷波器需要设置合适的宽度,宽度过窄可能会遗漏谐振频率附近的振动信号,过宽则会引起较大的相位滞后;陷波器深度不能过深,容易引起系统不稳定,过浅则无法抑制机械谐振。

有了上述的整定经验,本文使用一种基于信号频谱的整定策略进行陷波器参数整定[10],假定检测信号的频谱图如图4所示。

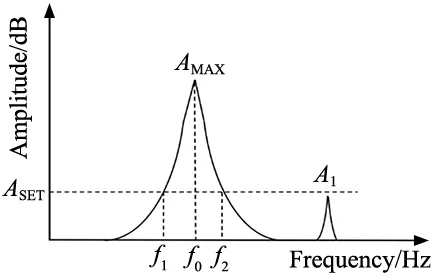
图4 整定陷波器参数的信号频谱

(1)陷波器可以对陷波频率的信号幅值进行最高的衰减,因此陷波器的陷波频率应当设定为频谱图中的幅值最高的信号频率f0:

fnotch=f0

(6)

(2)通过测试设置一个频谱检测的阈值ASET,当检测的某个频率信号的幅值低于此值时,不将其视为谐振频率部分。查找频谱图上f0两侧幅值等于ASET的两个频率点f1、f2,由式(7)计算得到陷波器宽度参数:

wide=2*max{|f1-f0|,|f2-f0|}

(7)

(3)陷波器深度参数由式(8)进行整定:

(8)

式中:dmin与dmax为陷波器深度设定边界。

2.2 陷波器离散化

在实际的计算机控制系统中,cpu处理的都是数字量,因此在使用陷波器前还需要将其离散化为数字陷波器。使用双线性变换离散化陷波器,式(4)离散化之后的传递函数如下:

(9)

式中:

(10)

式中:n表示离散控制系统中陷波器采样频率与陷波频率的比值。

3 谐振频率检测方案

对伺服系统谐振抑制而言,若采用“先检测,后抑制”的策略需要参考的一个重要的性能指标就是检测出机械谐振频率所需要的时间。由第3节的分析可知基于信号频谱的陷波器参数整定策略需要获取检测信号的频谱值,根据频谱值计算得到谐振频率再进行陷波器的参数整定。当前市面上常见的驱动器通常都是采用FFT获取谐振频率。FFT采取先采样、后计算的方式进行频谱计算。当采样频率为1 kHz,采样点数为512点时,则光是完成采样过程的时间就占用了500 ms,再加上频谱计算的过程会导致检测过程时间过长,机械谐振会对设备造成一定程度的损害。

3.1 SDFT频谱算法

与FFT不同,滑动傅里叶变换(SDFT)采取边采样、边计算的方式进行频谱计算。SDFT将定时采样的信号储存在窗口长度为N的缓冲区中,每完成一次采样,SDFT会提取缓冲区数据以迭代的方式更新一次频谱值,因此可以在计算过程中随时获取信号频谱,大大减少了频谱计算时间[9]。

窗口长度为N的SDFT表达式如式(11)所示。

(11)

式中:x(n)与Xn(k)分别表示第n次采样时的输入值以及频谱图上第k点的幅值。由上式可知SDFT当前采样时刻的各频率点的幅值等于上一时刻的幅值加上当前采样与N次采样前的输入值之差,最后再乘一个系数。可以看出SDFT每采样一次便可计算出一个频谱,相比FFT而言大大加快了获得信号频谱的速度。

3.2 谐振频率的提取

SDFT计算得到的检测信号的频谱值以复数的形式储存在缓冲区中,考虑到频谱值是随信号采样不断更新,因此在执行谐振频率提取的操作之前,需要将某一时刻的频谱值拷贝到另外的缓冲区中,使用拷贝缓冲区提取谐振频率,提取算法流程如图5所示。

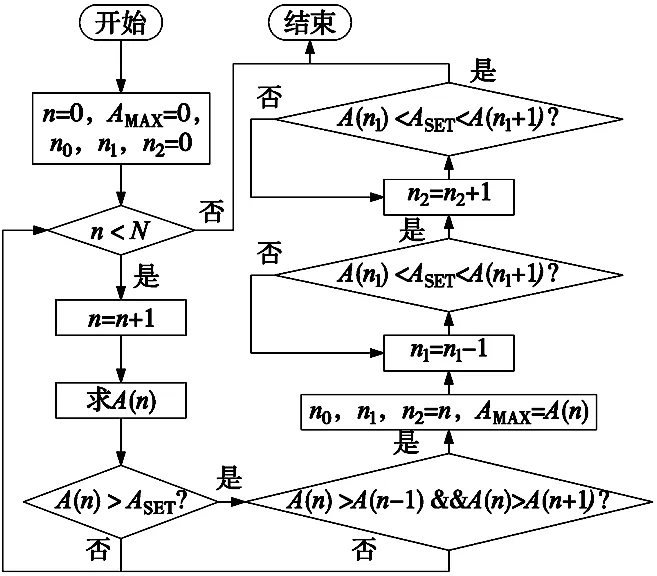
图5 谐振频率提取算法流程

算法首先根据频谱图计算各频率点的幅值,找出其中的最大值,此最大值若高于频谱检测阈值ASET,则将此处的频率点视为图4中的谐振频率点f0;在谐振频率点左右分别找到沿坐标轴两侧第一个幅值小于ASET的两个频率点,将此两个频率点分别视为图4中的f1、f2,以此可以完成谐振频率的计算以及方便后续陷波器参数整定。

4 实验验证

本文以永磁同步伺服控制系统作为实验对象,搭建谐振检测抑制平台如图6所示。实验选用的电机型号为06040A,驱动器型号为B1S,DSP型号为TI的TMS320F280049,主频100 MHz;电机通过联轴器与柔性杆相连,杆的另一端接上惯量盘作为负载。电机运行时的速度、转矩、谐振频率等信息通过串口传到上位机进行显示;网络测振仪型号为TC-4850N,检测块以刚性连接的形式固定在工作台上,通过PC机可以显示振动数据。

图6 实验工作台

4.1 谐振频率检测

驱动器设置500 rpm速度给定,逐渐增大速度环比例增益,使电机在阶跃响应下发生机械谐振,电机运行发生尖锐的噪音,此时电机转速与转矩信号如图7所示。

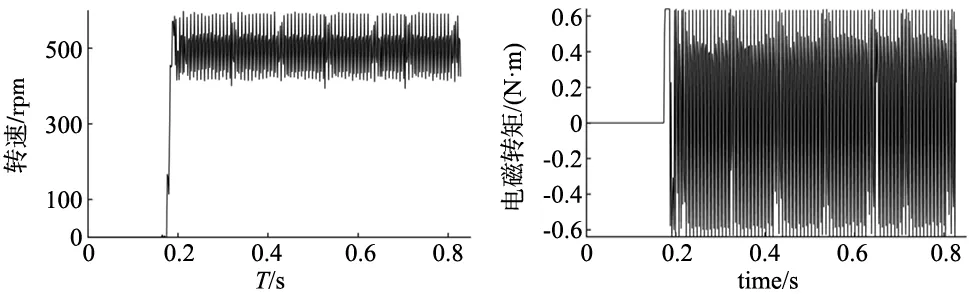
图7 机械谐振转速转矩波形

在电机发生谐振时开启测振仪进行数据采集,将采集的数据进行FFT分析,分析结果如图8所示。

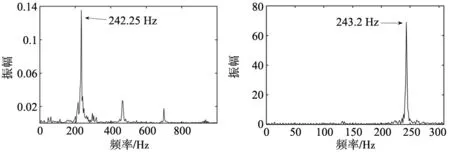
图8 机械谐振振动仪分析图9 电机转速SDFT分析

对电机谐振时刻的转速进行SDFT分析,采样率设为600 Hz,经过64次频谱计算后输出结果如图9所示。

两种检测方法都可以较为准确地反映出机械谐振频率,SDFT的64次频谱计算耗费的时间为106.7 ms,耗时短并且可以较为准确地反映出谐振信号的幅值信息。

4.2 基于自适应陷波器的谐振抑制

将SDFT频谱算法与3.2节中谐振频率提取算法写入驱动器中,如图10所示将自适应陷波器串入到电流环给定中。SDFT采样率为600 Hz,滑动窗口长度为512,计算在中断中完成,每64次SDFT迭代计算后输出一次频谱,提取谐振频率;若连续5次提取的谐振频率都相同,则将此频率视为有效的谐振频率,并按3.1节内容设置陷波器参数。

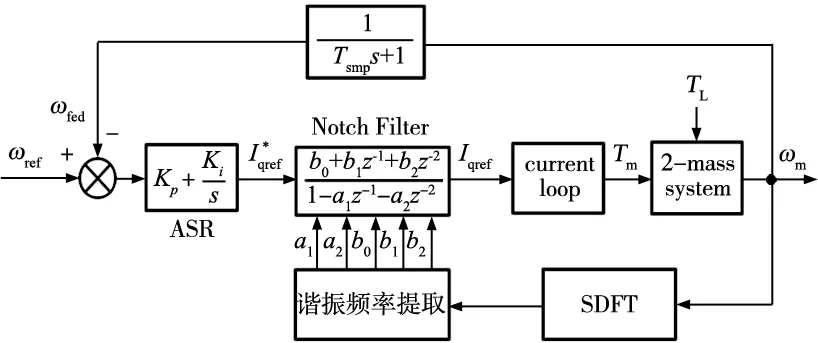
图10 自适应陷波控制框图

图11 自适应陷波器谐振抑制

设置500 rpm的转速给定信号,观察电机阶跃速度响应,调节速度环比例增益,使电机再此条件下发生谐振。在电机转速达到给定值100 ms后启用谐振频率检测与自适应陷波器功能,电机经751.9 ms后转速振荡得到抑制,实现转速的平稳输出。

5 结论

本文针对伺服控制系统中的机械谐振问题,提出一种基于信号频谱的整定策略整定自适应陷波器参数。采用SDFT频谱算法获取电机转速的频谱,根据信号频谱提取谐振频率,再经过判断推理后确定谐振频率,最后通过检测出的谐振频率进行自适应陷波器的参数整定,使能陷波器完成机械谐振的抑制。实验结果证明使用该方案可以准确检测谐振频率并在751.9 ms后抑制机械谐振。