混合Jaya算法在平面度误差评定中的应用*
2023-11-28汪顺利陈智超范晓骏
杨 洋,汪顺利,陈智超,范晓骏
(上海飞机制造有限公司,上海 021324)
0 引言
平面是构成任意物体的最基本几何元素之一,而平面度是衡量被测对象实际表面几何质量的重要参数,在零件平面以及基准面评价中具有非常重要的作用[1-2]。根据相关标准描述可知,平面度的评定算法最常用的是分为最小二乘法以及最小区域法[3],前者原理简单但是误差较大,而后者的评定算法精度更高[1],目前受到的应用和研究最为广泛。但是,最小区域法仅仅在标准中定义了准则,并没有提供具体的计算公式,因此,如何设计出以最小区域法为基准,满足零件平面测量数据状态的平面度评定算法是现阶段的主要研究内容。
在平面度误差评定的研究过程中,罗均等[1]通过改进基本的人工蜂群算法并将其应用于平面度误差评定中,提高了误差评定精度。王东霞等[4]将微分进化算法应用于平面度的最小区域法评定过程,并进行了算例验证。王军等[5]在平面度误差评定中引入了模拟生长优化算法,为平面度误差评定提供新的方法。柴光耀等[6]引入凸包理论计算空间型面的平面度误差,并通过实例验证了算法的正确性。厉玉康等[7]将差分进化算法进行了改进,提高了平面度评定的收敛速度。孙烁等[8]通过投影变换的方法将平面度误差转换为直线度误差评定,并验证了算法的可靠性。ZHANG等[9]将凸包算法和改进的粒子群算法应用到平面度误差计算过程,并通过实验验证了算法有效性。BALAZS等[10]应用遗传算法求解平面度误差的问题,作者通过多组实验验证了该算法在平面度误差问题上的优越性。夏亚涛[11]构建了新的粒子群算法的空间结构,提高了平面度评定的收敛精度。同年,娄建起等[12]以两条平行直线构造出平面的最小区域,提高了评定精度。但是,上述所提到的各类算法也存在着一定的局限性,比如算法构造复杂,算法参数多,工程化难度大,因此,需要进一步对平面度误差算法进行设计。
本文针对平面度的误差评定算法,基于最小区域法的数学模型,在基本Jaya算法的基础上,通过融合反向学习机制和下山单纯形法对解进行再次优化更新并增强局部搜索能力,从而进一步提高算法对平面度误差评定过程的迭代精度和速度。通过实测数据与相关算法进行对比验证,证明了算法的有效性,为平面度评定提供了可靠的计算方法。
1 平面度误差的最小区域法数学模型
对于构建平面度评价的最小区域数学模型,文献[2,5]进行了描述。根据标准中规定,平面度最小区域法是找寻一个基准平面Sd,存在平行于这个基准面Sd并包络所有测点的两个平行平面S1和S2,如图1所示,当包络所有实测点的平行平面S1和S2距离f最小时,该值为平面被测点的平面度误差。这就可以转化为平面测点到所需计算的基准平面Sd距离的偏差。到基于上述概念,建立满足最小区域法的数学模型如式(1)所示。
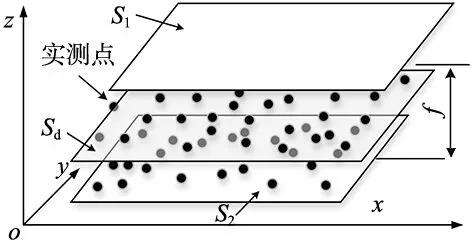
图1 平面度误差示意图
(1)
式中:Pi,x、Pi,y、Pi,z分别为平面的实测坐标数据,A、B、C为基准平面Sd的参数,fflatness为平面度误差值。
根据式(1)所示,最小区域法的平面度误差本质上是一种求解A、B、C及fflatness的非线性最小值优化问题[5]。
2 平面度误差评定算法设计
2.1 Jaya优化算法
Jaya为梵文,意为胜利者,该算法是新型群体智能优化算法[13],算法具有参数设置少,结构简单,全局搜索能力强的特点,对于复杂的非线性优化问题可以有效的进行求解,已经被应用于多个领域[14-15]。其算法主要步骤为:
步骤1:输入所需分析问题的数据并初始化参数,包括种群数量N,问题维度D,最大迭代次数T,解空间的上下限Xmax和Xmin并随机生成初始解集X={X1,X2,…,Xn};
步骤2:将步骤1中的初始解集X带入目标函数(1)中计算f(X1)到f(XN)的值,并将计算所得的目标函数值f(Xi)进行排列,对于最小化问题,每一次迭代中,max(f(X))对应的解为最差解Xw,min(f(X))对应的解为最优解Xb,对于每一个解的维度Xi,j会根据式(2)产生一个新值Xnew,i,j;
Xnew,i,j=Xi,j+rand·(Xb,j-|Xi,j|)-rand·(Xw,j-|Xi,j|)
(2)
式中:rand为(0,1)之间的随机数,j表示每类解第j维的值。
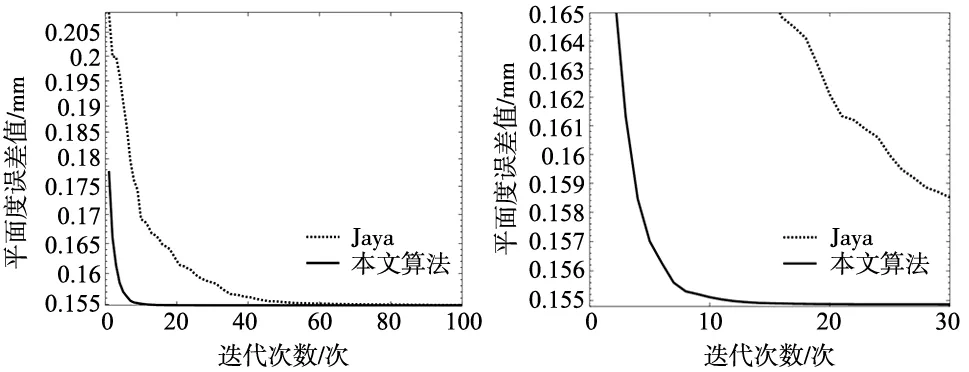
步骤3:将新的解Xnew,i带入到目标函数值中,然后将新解f(Xnew,i)与原来的解f(Xi)进行对比,当f(Xnew,i) 步骤4:判断算法是否满足迭代次数N,当达到最大迭代次数时,输出最优解Xb及其目标函数值f(Xb),否则返回步骤2继续计算。 对于基本的Jaya优化算法,解的空间分布影响着算法的全局寻优能力,为了提高初始种群以及迭代过程中种群的多样性,本文通过两次引入反向学习[16](opposition-based learning,OBL)策略用以提高算法的全局探索能力: XOBL,i=Li+Ui-Xi (3) 式中:Li为每个维度的上限,Ui为每个维度的下限。 下山单纯形法也称Nelder-Mead算法,不同于Jaya算法,Nelder-Mead算法[17]具有很强的局部搜索能力,其本质上是多元函数局部最优解求解算法。但是,该方法需要良好的初值,才能够获取高精度结果。Nelder-Mead算法的基本原理是将问题维数为D的函数构建D+1个顶点的单纯形,采用反射、扩张、收缩以及压缩等步骤,将目标函数最大的顶点通过不断迭代直到接近最优解。计算流程为: 步骤1:算法初始化,通过初值X0,构成D+1个顶点;并将所有点带入到目标函数(1)中,并将目标函数值按照f(X1)≤f(X2)≤…≤f(XD+1)由小到大升序排列,对于最小化问题,删除目标函数值所对应的最大的单纯形点f(XD+1),并计算剩余顶点的重心坐标Xg,如式(4)所示: (4) 步骤2:首先通过反射算法对最差解XD+1进行更新,如式(5)所示,当f(X1)≤f(Xr)≤f(XD)时,则用Xr替换XD+1建立新的单纯形。如果f(X1)>f(Xr),进入步骤3的计算。 Xr=Xg+α·(Xg-XD+1) (5) 式中:α为反射系数。 步骤3:当步骤2中的f(Xr) Xe=Xg+β·(Xr-Xg) (6) 式中:β为延伸系数。 步骤4:当反射算法步骤2得到的解Xr满足f(XD)≤f(Xr)≤f(XD+1)时,则采用外收缩算法生成新解Xc,如式(7)所示。当f(Xc) Xc=Xg+δ·(Xr-Xg) (7) Xc=Xg+δ·(XD+1-Xg) (8) 式中:δ为收缩系数。 步骤5:更新除当前最优解之外所有的顶点,如式(9)所示,构造出新的单纯形点,返回步骤2,进行下山单纯形迭代; Xnew=X1+ε·(Xi-X1) (9) 式中:ε为压缩系数。 步骤6:根据上述内容,当下山单纯形迭代完成时,同时完成空间平面的拟合评价,输出平面度的评价结果以及理想平面的参数。 为了提高平面度误差评定的计算精度和收敛速度,结合上述内容,本文所提的算法流程为: 步骤1:初始化Jaya与Nelder-Mead的算法参数,包括初始化种群数量N,问题维度D,最大迭代次数T,上下限维度Xmax和Xmin,反射系数α,延伸系数β,收缩系数δ,导入平面测点数据,进入步骤2; 步骤3:进入Jaya算法迭代计算流程,根据2.1节中步骤2和步骤3所示,对种群进行解的更新,并在每次迭代过程中,对种群中最差的10%的解采用2.2节的反向学习机制再次进行更新,进入步骤4; 步骤4:在Jaya算法每一次迭代计算完成后,按照2.3节所述的下山单纯形法,将最优解Xbest作为初始解X0输入到单纯形算法进行进一步的局部搜索机制中,进入步骤5; 步骤5:判断算法是否满足最大迭代次数T,如果满足,输出最优解Xb及其适应度函数值f(Xb),其中该适应度函数值f(Xb)为最终所得到的测点数据平面度误差值;否则返回步骤3。 算法流程如图2所示。 图2 本文平面度算法流程 为了验证算法在平面度误差评定中的性能,对零件表面进行测量数据的获取,数据如表1所示。基本Jaya和本文算法实现工具为MATLAB2019,电脑内存为16 G,操作系统为Windows 11,算法维度为D=3,迭代次数T=100,上限Xmax=30,下限Xmin=-30,系数分别为α=1,β=2,δ=0.5,ε=0.5。 表1 平面度测量值 (mm) 分别将平面数据带入到遗传算法(genetic algorithm,GA),粒子群算法(particle swarm optimization,PSO),基本Jaya和本文所提算法中运行30次,迭代曲线如图3所示,平面度评价的基准平面如图4所示。平面度误差计算结果如表2所示。 表2 平面度误差计算结果 (mm) 图3 算法迭代曲线图 图4 平面度基准平面 如图3所示分别为GA、PSO、基本Jaya算法以及本文算法4种优化算法对最小区域法下的平面度误差评定进行求解。结合表2可知,在30次计算结果的平均值中,GA计算结果为0.066 21 mm,PSO为0.066 09 mm,Jaya为0.066 07 mm,本文算法为0.066 06 mm,平面度误差评定结果最小,计算精度最高。从图3可以看到,从迭代收敛过程中,GA迭代约在62次时算法收敛,PSO迭代约在51次算法收敛,基本Jaya迭代约在38次算法收敛,本文所提算法迭代约23代时算法收敛,因此,收敛速度最快。图4为满足式(1)的基准平面,通过该平面可以获取到本次采集的平面数据点的满足最小区域法下的平面度误差值。 为了进一步验证所设计算法在平面度误差评定中的性能,选用相关文献[18]的数据进行测试验证。分别将平面数据带入到基本Jaya和本文所提算法中运行30次,迭代曲线如图5所示,图6为图5的局部放大图。基准平面如图7所示。计算结果如表3所示。 表3 平面度误差计算结果 (mm) 图5 算法迭代曲线图 图6 算法迭代曲线放大图 图7 平面度基准平面 表3分别为模拟植物生长算法(plant growth simulation algorithm,PGSA)[5]、基本蜂群算法(artificial bee colony,ABC)[1]、改进人工蜂群算法(modified artificial bee colony,MABC)[1]、基本Jaya算法以及本文算法5种优化算法对最小区域法下的平面度误差评定进行求解的计算结果。其中,PGSA计算结果为0.1550 mm,ABC计算结果为0.154 895 mm,MABC为0.154 87 mm,Jaya为0.154 90 mm,本文算法为0.154 87 mm,平面度误差评定结果与MABC同为最小,计算精度最高。结合图5、图6可以看到,从迭代收敛过程中,本文所提算法约在第25代时收敛,收敛速度快于约40次的MABC算法,提升了37.5%。图7为平面度误差的基准平面,平面度误差能够满足最小区域原则。 为了提高平面度误差评定的算法精度与迭代收敛速度,提出了一种混合Jaya算法的平面度误差评定算法。在基本Jaya算法的基础上,融合两次反向学习机制与下山单纯形法提升迭代过程解的质量和局部搜索能力,从而进一步提高算法的计算精度和迭代速度。通过构建平面度误差的最小区域法数学模型与相关算法,进行了实例验证与对比分析,结果表明,混合Jaya算法不仅可以提高平面度误差评定精度,也可以在保证精度的基础上,提升算法的收敛速度。2.2 反向学习机制
2.3 下山单纯形法
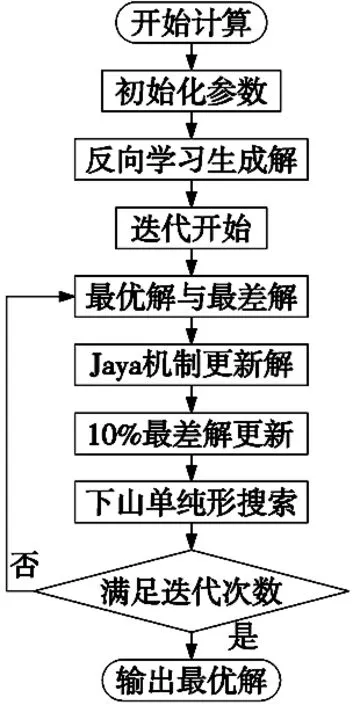
2.4 平面度误差评定算法流程
3 实验验证与分析





4 结论
