多关节工业机器人BSMC与EPCH协同优化控制*

杨晓宇,于海生,李 哲

(青岛大学a.自动化学院;b.山东省工业控制技术重点实验室,青岛 266071)

0 引言

工业机器人是工业领域中的多关节机械手或多自由度(degree of freedom,DOF)的机械装置,具有灵活运动和工作效率高的优点[1]。因此,多关节工业机器人广泛应用于装配、汽车制造、焊接等行业。随着信息技术和现代制造业的快速发展,如何使多关节工业机器人同时具有优越的控制精度、响应速度和运行稳定性,成为了机器人关节伺服控制相关领域的研究难点[2-3]。机器人关节伺服系统包括驱动装置、传动装置和机器人本体3部分,其中驱动装置大多采用永磁同步电机(permanent magnetic synchronous machine,PMSM)[4],传动装置主要采用谐波减速器。PMSM通过谐波减速器将电磁转矩转换为关节转矩,以驱动机器人关节完成规定的运动和功能。

在多关节工业机器人的控制算法方面,国内外的研究学者提出了许多控制方法,如反步控制、滑模控制和模糊控制等。反步控制(backstepping control,BC)算法简单,能使控制器的设计过程系统化和结构化。在机器人关节伺服系统的位置控制中,BC通常与智能方法或其他非线性方法相结合[5-6]。滑模控制(sliding mode control,SMC)对外部干扰和参数摄动具有很强的鲁棒性,且具有调控快速的优点,因此被广泛应用于非线性系统的控制[7-8]。模糊控制依赖研究人员的工作经验,且稳态误差通常较大,控制效果不理想。以上控制方法都是基于信号控制观点,虽然具有良好的动态性能,但系统的稳态性能较差[9-10]。

目前,基于能量控制观点的方法引起了研究学者们的重视,ORTEGA、BEATTIE等[11-13]提出了端口受控哈密顿(port-controlled hamiltonian,PCH),该控制方法把非线性系统看作为能量变化装置,既有能量的存储也有能量的耗散。并且把哈密顿函数作为Lyapunov函数,简化了直接选取Lyapunov函数的过程。

基于以上信号控制观点和能量控制观点,本文提出了协同优化控制策略。该策略可以使机器人关节伺服系统兼顾信号控制器和能量控制器的优点,同时做到快速调控和准确跟踪。首先分别设计了BSMC控制器与EPCH控制器,然后采用高斯函数作为协同优化控制系数,并进一步设计了协同优化控制策略。最后,仿真实验结果表明,协同优化控制策略可以使多关节工业机器人同时具有优越的快速性和准确性。

1 机器人关节伺服系统数学模型

本文以六自由度机器人关节伺服系统作为研究对象,该系统包括PMSM、谐波减速器和机器人本体3部分。考虑到关节间的摩擦特性,基于LuGre摩擦模型的机器人关节伺服控制系统数学模型为[14]:

(1)

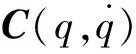
2 控制器设计

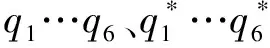
2.1 BSMC控制器设计

(2)

步骤1:机器人关节的位置误差定义为:

(3)

式中:q*为机器人关节的期望位置。

对式(3)求导,得到:

(4)

(5)

选取步骤1时的系统Lyapunov函数为:

(6)

结合式(5)和式(6)得:

(7)

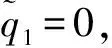
步骤2:对式(4)进行求导,得到:

(8)

选取传统滑模面为:

(9)

式中:β为对称、正定常值矩阵。

对式(9)求导得:

(10)

定义步骤2时的Lyapunov函数为:

(11)

对式(11)求导得:

(12)

若e2=0,设计反步滑模控制器为:

(13)

式中:ρ为对称、正定常值矩阵,λ为正常数。

将式(13)代入式(12)中,得出:

(14)

此时机器人关节伺服系统是渐近稳定的。

2.2 EPCH控制器设计

对于非线性系统,带有能量耗散的PCH模型可以表示为[15]:

(15)

式中:x、u、y分别为系统的状态向量、输入向量和输出向量,J(x)为互联矩阵,且J(x)=-JT(x),表示系统内部互联结构;R(x)为阻尼矩阵,且R(x)=RT(x),反映了系统端口上的电阻结构;g(x)反映系统的端口特性,H(x)为哈密顿函数,定义为系统内部存储的总能量。

定义机人关节的状态变量、输入变量分别为:

(16)

τe=[τe1,τe2,…,τe6]T

(17)

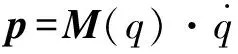
机器人关节伺服系统的哈密顿函数为:

(18)

式中:V(q)为机器人关节的势能。

六自由度机器人关节的PCH模型为:

(19)

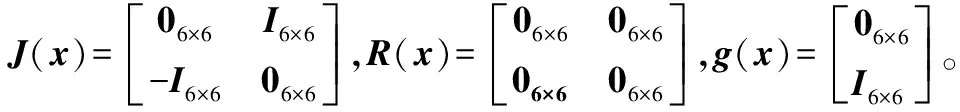
定义机器人关节的状态误差为:

(20)

则机器人闭环控制系统期望Hamiltonian函数为:

(21)

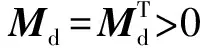
写成EPCH形式,可以表示为:

(22)

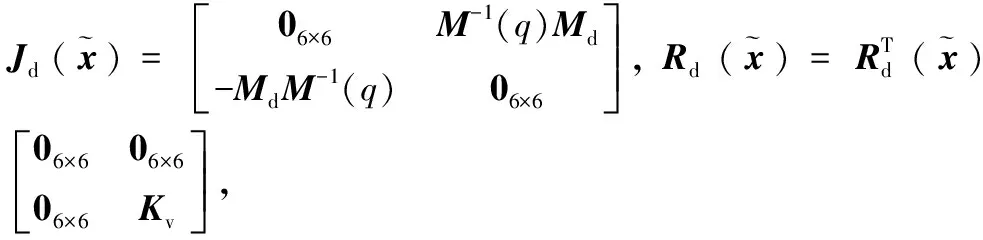
根据式(19)、式(20)和式(22)可得:

(23)

由式(23)得到机器人关节转矩为:

(24)

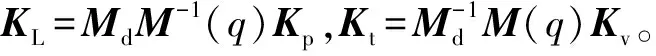
式(21)描述的哈密顿函数即为Lyapunov函数,则闭环系统的Lyapunov函数为:

(25)

对式(25)求导,并将式(1)和式(24)代入得:

(26)

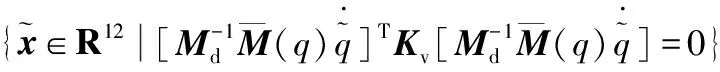
2.3 协同优化控制策略

为了使机器人关节伺服系统同时具有良好的快速性与准确性,设计了协同优化控制策略。该策略通过引入协同优化控制系数,在BSMC控制器与EPCH控制器之间进行平滑切换,使系统兼顾以上两种控制器的优点。

由文献[16]可知,高斯函数对系统的协同控制效果最好。因此,本文直接采用高斯函数作为协同优化控制系数,并设计协同优化控制器为:

(27)

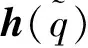
协同优化控制系数曲线如图2所示。

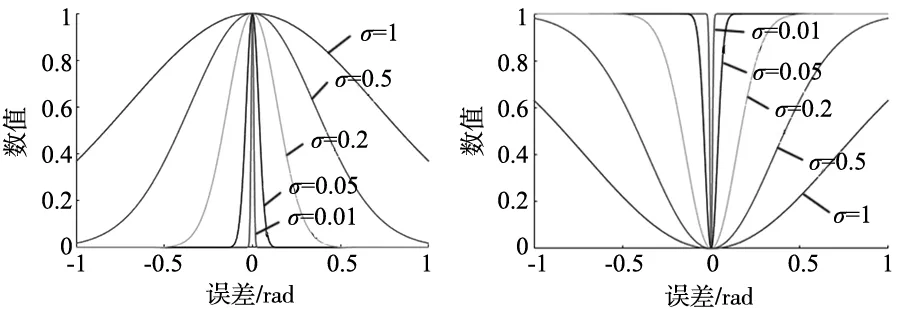
图2 协同优化控制系数曲线

3 仿真实验结果分析

为验证协同优化控制策略的有效性,在MATLAB/Simulink环境中对机器人关节伺服系统的1、2关节进行建模和仿真。

各参数取值为:m1=1.5 kg,m2=0.8 kg分别为机器人1、2关节质量,l1=0.24 m,l2=0.14 m分别为机器人1、2关节长度。BSMC中λ=5,ρ=diag{200,200},β=diag{50,50};EPCH中KL=diag{50000,50000},Kt=diag{3000,3000},尺度参数σ=diag{0.01,0.01}。

仿真1:为验证BSMC在动态性能上的优越性,将BSMC与反步控制(backstepping control,BC)进行仿真对比,图3为机器人1、2关节分别采用BSMC与BC的阶跃响应跟踪曲线。

(a) 关节1的跟踪曲线 (b) 关节2的跟踪曲线

由图3可知,两个关节分别采用BSMC和BC时,采用BSMC能够使系统的动态响应速度更快,快速性更好。

仿真2:为验证协同优化控制策略的有效性,将协同优化控制策略与单独采用BSMC、单独采用EPCH进行仿真对比,图4为机器人1、2关节分别采用以上3种控制方法的阶跃响应跟踪曲线。

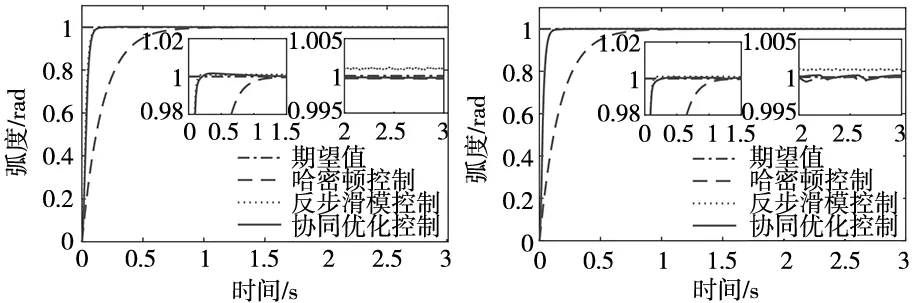
(a) 关节1的跟踪曲线 (b) 关节2的跟踪曲线

由图4可知,单独采用BSMC时,系统的上升时间为0.15 s左右,稳态误差为1.5×10-3rad;单独采用EPCH时,系统的上升时间为1.16 s左右,稳态误差为7×10-5rad;采用协同优化控制策略时,系统的上升时间为0.25 s左右,稳态误差为7×10-5rad。因此,协同优化控制策略与单独采用BSMC相比,跟踪精度提高了约95%;与单独采用EPCH相比,上升时间快了0.9 s左右。3种控制方法下的具体性能指标如表1所示。

表1 3种控制方法下的性能指标

由表1的性能指标数据可知,单独采用BSMC时,机器人关节具有较短的上升时间,但稳态误差较大;单独采用EPCH时,机器人关节具有较小的稳态误差,但上升时间较长;当采用协同优化控制策略时,机器人关节具有较短的上升时间和较小的稳态误差。

因此,协同优化控制策略可以兼具BSMC与EPCH各自的优点,使机器人关节伺服系统同时具有良好的快速性与准确性。

4 结论

本文为提高机器人关节伺服系统的控制性能,提出了BSMC与EPCH的协同优化控制策略。当系统处于动态阶段时,BSMC起主导作用;当系统处于稳态阶段时,EPCH起主导作用。该策略采用基于关节位置误差的高斯函数,根据误差大小实时对BSMC与EPCH进行平滑切换,改善了系统的动态与稳态性能。仿真实验结果表明,与单独采用BSMC相比,所提出的协同优化控制策略使系统的跟踪精度提高了约95%;与单独采用EPCH相比,所提出的协同优化控制策略使系统的上升时间快了0.9 s左右。因此,BSMC与EPCH协同优化控制策略能够使机器人关节同时具有快速的响应速度与准确的跟踪精度。