非线性不确定机器人复合滑模非脆弱H∞位/力控制*

刘树博,李 智,赖招宇,罗先喜,李跃忠,刘建文

(东华理工大学a.江西省康复辅具产业技术研究院;b.机械与电子工程学院,南昌 330013)

0 引言

机器人进行接触性作业的过程中,其末端既要沿约束环境表面做理想的轨迹运动,又要对环境施加一定的作用力。此外,机器人是一类具有非线性、强耦合和不确定性的系统,且工作环境复杂多变。因此研究一种能够同时抑制不确定性及扰动的非线性位/力控制策略,具有十分重要的意义。

针对机器人的位/力控制问题,国内外学者对其进行了研究,并取得了一定成果[1-4]。滑模控制是一类特殊的非线性控制[5],已被成功应用于机器人位/力控制中。LI、ZHU等[6-7]针对约束重构机器人位力控制问题,提出一种滑模自适应神经网络的控制算法,仿真结果表明了所提方法的有效性。针对机械臂位力混合控制问题,LUIS等[8]设计了滑模力控制器和低优先级跟踪控制器,保证位/力的有效跟踪控制。HAMED、ZHENG等[9-11]将模糊逻辑与传统滑模相结合,提出了自适应模糊滑模控制策略,降低了机械臂位力跟踪误差,提高了控制精度。PENG等[12]提出了一种适用于移动机器人的滑模自适应位/力控制,利用Lyapunov定理对系统稳定性及位/力跟踪误差的有界性进行了证明,仿真和实验结果验证了所提算法的有效性和鲁棒性。CAO等[13-14]针对受限机械臂位/力控制问题,提出了一种有限时间自适应扩展终端滑模控制,在有限时间内保证了位力误差收敛到零。

到目前为止,设计得到的滑模控制增益大多为固定矩阵,在面对机器人时变参数和外界干扰时,无法满足控制性能的更高要求。此外,具有固定增益的自适应滑模控制策略,虽然提高了控制性能,但其中可变参数的自适应学习率大多是由设计者通过凑试而得,缺乏理论指导。因此研究一种依赖于系统状态和参数的变增益滑模控制,来提高控制性能是十分必要的。

SOS是非线性控制系统设计与分析中的一门新兴理论[15],可将复杂的多项式非线性控制问题转化为凸优化问题,目前已成功应用于航天器和卫星等非线性时变系统[16-21,23],但对于非线性不确定机器人及滑模控制策略,该理论却鲜有涉及。鉴此,针对受环境约束的时变机器人模型,考虑控制器摄动,将SOS理论与滑模控制相结合,提出复合滑模非脆弱H∞控制,给出了非线性变参数状态反馈增益存在的条件。在进行了详细的理论推导后,对双关节机器人进行仿真分析,并与已有算法进行比较,进一步验证了所提策略的有效性和优越性。

1 预备知识与问题描述

1.1 预备知识

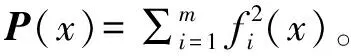
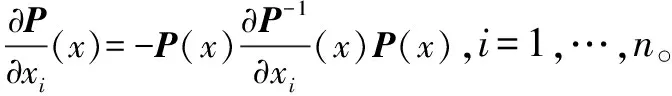
引理2[15]:若P(x)∈φSOS成立,当且仅当存在一个半正定矩阵Q,使得P(x)=Z(x)QZ(x)成立,其中Z(x)是关于x的单项式向量。

引理3[16]:取D和V为适维多项式实矩阵,对任意满足不等式ηT(t)η(t)≤I且η(t)的,则以下两条件等价:

(1)Dη(t)V+VTηT(t)DT<0。

(2)∀σ∈[0,+∞),使得σDDT+σ-1VTV<0。

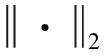
1.2 机器人位/力控制问题描述

考虑一个具有环境约束的刚性n连杆机器人,在关节空间中的静态环境约束和机器人动力学模型分别描述为:

Ψ(q)=0

(1)

(2)

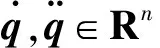
考虑到机器人的参数摄动,将式(2)改写为:

(3)

(4)

当机器人末端与环境接触时,由于受环境约束的影响,使机器人失去了m个自由度[13],因此可用n-m个关节变量来描述受约束系统的运动情况。定义向量q=[q1,q2]T,其中q1∈Rn-m代表机器人未受环境约束部分,q2∈Rm代表受环境约束部分。由于Ψ(q)满秩,基于隐函数存在定理,q2可用q1表示,即存在函数q2=φ(q1)。然后,采用坐标变换法获取约束机器人的降阶动力学模型。引进矩阵:

H(q1)=[In-m∂φT/∂q1]T∈Rn×(n-m)

则有:

(5)

(6)

将式(5)和式(6)带入式(4),可得到受约束机器人动力学方程为:

(7)

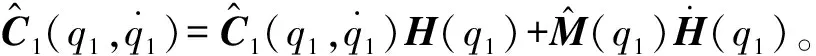
对式(7)两边同时左乘矩阵HT(q1),结合机器人性质[22],可得等价的机器人降阶动力学模型为:

(8)

式中:

令qd(t)和λd(t)分别为机器人期望轨迹和期望力输出,位/力跟踪误差可分别表示为:

(9)

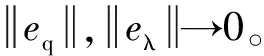
2 CSNH位/力控制

注1:为方便书写,本文作如下简写:F(x,t,…)=F(·),其中“·”代表多个自变量。

2.1 复合位/力滑模面设计

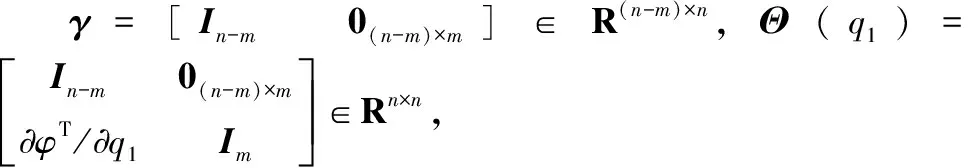
假设1:机器人期望力λd∈Rm及其一阶导数,机器人期望轨迹qd∈Rn-m及其一、二阶导数,均为有界变量。

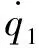
复合滑模面函数定义如下:

s=γT·s1+JT·s2

(10)

式中:s∈Rn,s1∈Rn-m为轨迹跟踪滑模函数,s2∈Rm为力跟踪滑模函数,二者具体形式分别为:

(11)

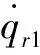
(12)

对式(10)两端左侧分别乘以γΘT(q1),可得γΘT(q1)s=s1+γΘT(q1)·JT·s2,根据机器人性质对其化简可得s1=γΘT(q1)s,当系统到达滑模面s=0处时,滑模函数s收敛于0,此时滑模函数s1→0;由式(10)可得,JTs2=s-γT·s1,由于J(q)的行满秩为m和s2∈Rm,即可得到s2→0。因此当s=0时,滑模函数s1、s2→0,轨迹跟踪误差eq和力跟踪误差eλ将会在有限时间内收敛到0。

2.2 复合滑模控制策略设计

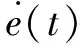
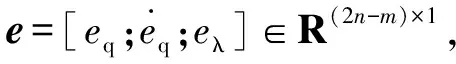
(13)

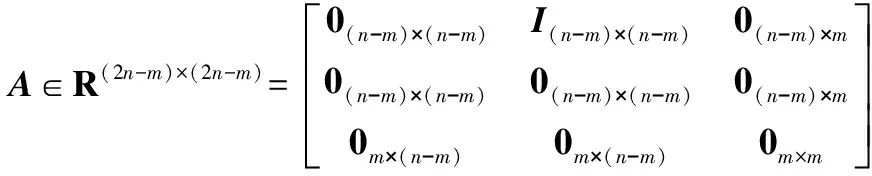
根据机器人降阶误差模型(13),设计如下复合滑模控制策略:

u=uα+uβ+uΩ

(14)

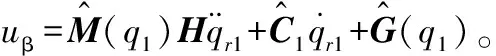
很显然,式(14)为典型的复合滑模H∞控制策略,其性能取决于控制律uΩ的优劣。在实际应用中,由于受到现场诸多因素的影响,控制器输出会产生摄动,从而具有一定的脆弱性。由于控制器脆弱性的存在,使理想的位/力控制策略无法完美地执行,降低了机器人系统的稳定性及控制精度。

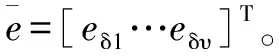
将控制律(14)带入误差状态空间模型(13),可得增广误差闭环受扰系统模型为:

(15)

式中:ω(χ(·))∈R(n-m)×1表示闭环系统集总扰动量。

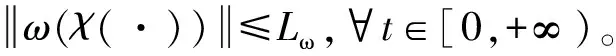
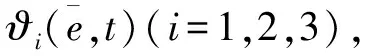
(16)

(17)

(18)

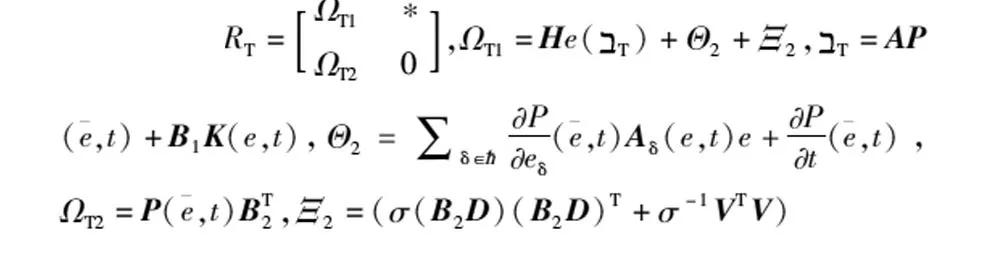
证明:定义Lyapunov函数V(e,t)为:

(19)

接下来,将Lyapunov函数V(e,t)对时间t求导,并结合闭环系统模型(15)可得:

(20)

对于ω中的未知量ωξ,考虑其具有以下形式:

ωξ(χ(·))=D(χ(·))η(t)V(χ(·))

式中:D(χ(·)),V(χ(·))∈R(n-m)×(n-m)为已知多项式矩阵,η(t)为未知时变矩阵,且满足ηT(t)η(t)≤I。根据引理3,式(20)可化简为:

(21)

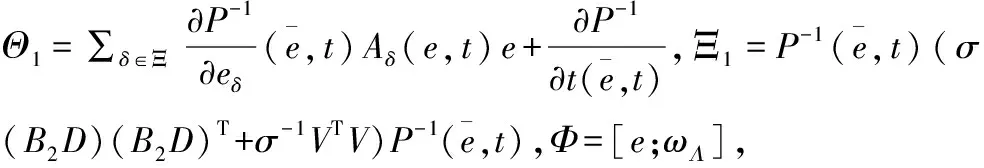
由式(18)可得,ℜT是半负定,即:

ℜT+ϑ3I≤0

(22)

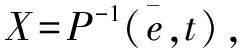
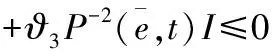
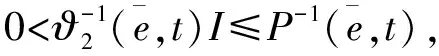
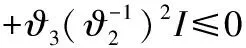
(23)

对式(23)左右两端分别乘以ΦT及Φ,可得:

基于式(19),上式可转化为:

(24)

对式(24)两边在[t0,t]上进行积分,得:

结合式(19)和(24),对其做进一步化简得:

(25)

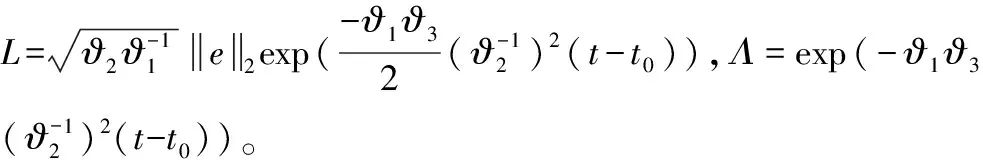
综上所述,误差系统模型(13)在复合滑模控制策略(14)的作用下全局指数稳定。证毕。

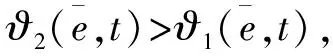
(26)

成立,则该系统为具有H∞干扰抑制的全局指数稳定。

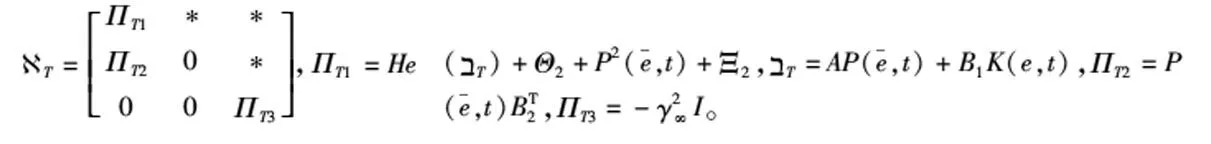
证明:显然,式(25)成立,意味着式(18)成立,此时定理1成立,系统全局指数稳定。

定义如下形式的Lyapunov函数:

(27)

由定理1可知,Lyapunov函数V(e,t)正定有界。

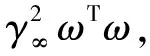
对上式进行化简,定义增广向量μ=[e;ωΛ;ω],可得:

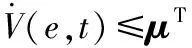
(28)

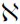
由式(25)知:

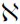
(29)

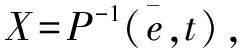
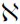
(30)

结合式(28)和式(30)可得:

当V(0)=0时,对不等式两边关于时间t=0到t→∞积分,则有:

从而实现对扰动的H∞抑制。证毕。

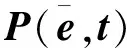
基于定理2,可以得到如下推论。

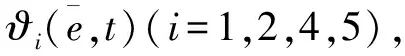
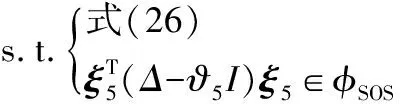
(31)

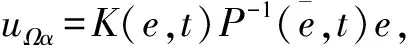
(32)

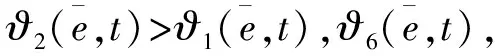
(33)

成立,则系统(32)H∞状态反馈控制问题可解。

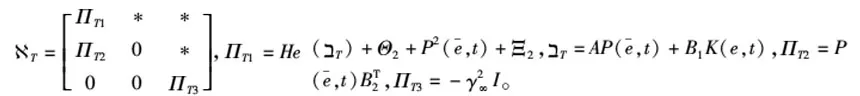
3 仿真分析

本节以双连杆机械臂为例进行设计,其模型如下:

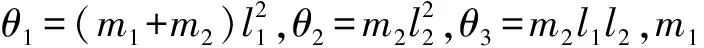
假定二自由度双连杆机械臂终端执行器沿约束圆表面运动,其约束方程为Ψ(X)=x2+y2-r2=0,X=[x,y]T,r表示圆半径。双连杆机械臂运动学方程为:

3.1 仿真实例1

根据推论1,利用SOS工具箱对优化问题(31)进行求解,得到最优H∞性能γ∞和增益矩阵P如下:

γ∞=0.9378

由于变增益矩阵K精确度较高,多达12位小数,考虑篇幅限制,K矩阵和复合控制律不再给出。设置滑模面参数kq=20,nΩ=100;期望轨迹和期望力为:

情况1:机器人无扰动,无控制器摄动;

情况2:只考虑外部集总扰动Γ(·);

情况3:只考虑控制器摄动ΔK(·);

情况4:外部集总扰动Γ(·)+控制器摄动ΔK(·)。

分别将上述4种情况的实际输出轨迹与期望轨迹进行对比,仿真结果如图1所示。通过比较发现:①在理想情况下,CSNH控制策略使机器人具有良好位/力跟踪效果,表明了文中机器人数学模型及控制算法推导的正确性。②在情况2～4中,机器人仍具有与理想情况1类似的跟踪效果,展现出了CSNH控制策略对系统扰动和控制器摄动较好的抑制能力,验证了算法的鲁棒性和非脆弱性。

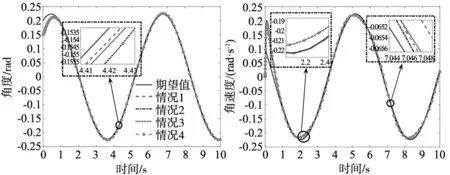
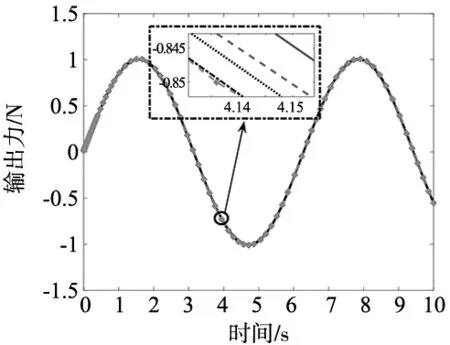
图1 机器人跟踪曲线图

3.2 仿真实例2

文献[24]以末端受限的刚性机械臂为研究对象,通过滑模自适应算法和RBF神经网络滑模算法对机器人进行位/力控制,并给出了Lyapunov证明过程,确保位/力跟踪误差快速收敛至0。为进一步说明所提算法的优越性,与文献[24]的两种滑模控制算法进行对比,仿真结果如图2所示,其中滑模面参数选取为kq=100,nΩ=2000,期望轨迹和期望力分别选为:

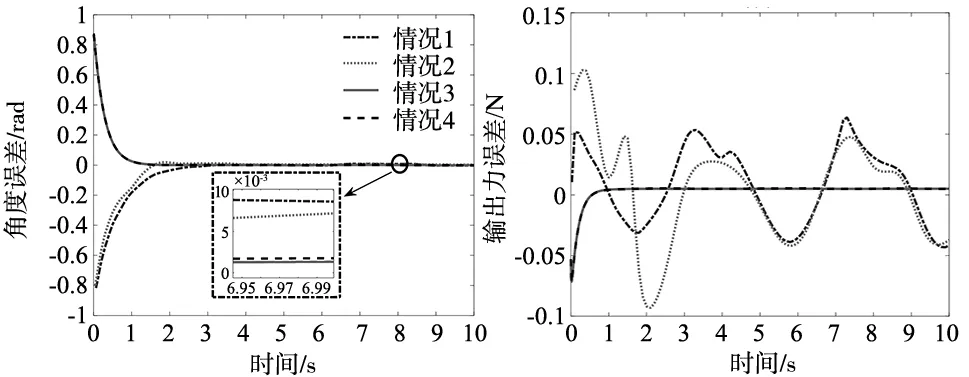
图2 位/力跟踪误差对比图

仿真内容包括以下4个方面,即:

情况1:文献[24]滑模自适应算法+F(·)+无控制器摄动;

情况2:文献[24] RBF神经网络滑模算法+F(·)+无控制器摄动;

情况3:CSNH位/力控制+无集总扰动+无控制器摄动;

情况4:CSNH位/力控制+ΓM(·)+F(·)+控制器摄动ΔK(·)。

从位/力跟踪误差曲线对比可知:①情况4中的机器人具有和情况3相似的曲线输出,表明了CSNH位/力控制降低了系统集总扰动和控制器摄动对系统造成的负面影响,取得了近似于理想情况的控制效果。②虽然情况4中的机器人同时受到ΓM(·)、F(·)和控制器摄动ΔK(·)三种干扰因素影响,与只考虑单一干扰因素F(·)情况1～2相比,系统输出曲线仍具有光滑无超调、收敛速度更快、调节时间更短、稳态误差更小的优点,表明了CSNH位/力控制比文献[24]中的两种滑模控制算法具有更高的控制精度及更优的控制效果。

3.3 仿真实例3

选取文献[13]中的机器人模型参数,利用SOS工具箱对优化问题(31)进行求解,所求得的最优H∞性能γ∞和增益矩阵P如下:

γ∞=0.9312

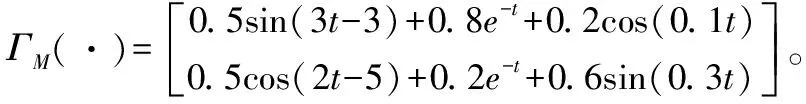
文献[13]设计了自适应终端滑模位/力控制器,并给出了自适应律以保证其位/力跟踪误差在有限时间内收敛到0。为进一步说明所提算法的优越性,与文献[13]的两种滑模控制算法进行对比,仿真结果如图3所示,其中滑模面参数选取为kq=250,nΩ=23 000,期望轨迹和期望力分别选为:

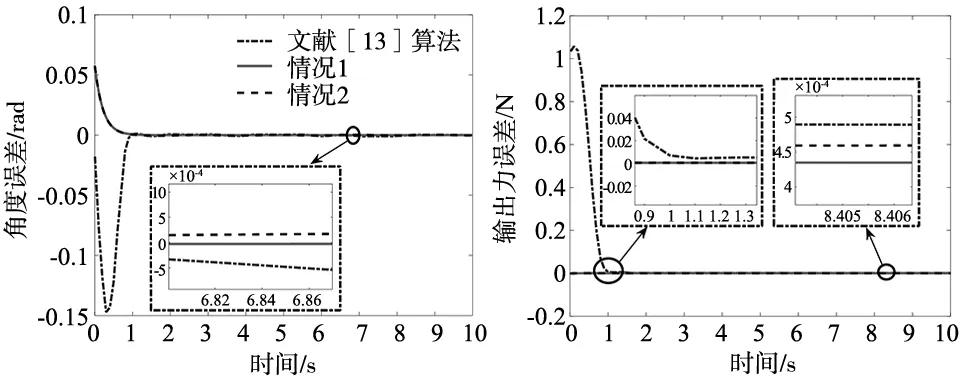
图3 位/力跟踪误差对比图

仿真内容包括以下两个方面,即:

情况1:CSNH位/力控制+无集总扰动+无控制器摄动;

情况2:CSNH位/力控制+ΓM(·)+F(·)+控制器摄动ΔK(·)。

从位/力跟踪误差曲线对比可知:①情况2中的CSNH位/力控制取得了与理想情况1相似的控制效果。②与文献[13]算法相比,CSNH位/力控制系统输出曲线无超调,收敛速度更快,稳态误差更小,且位/力误差绝对值积分更小,体现出了更优的暂态和稳态性能。

4 结论

针对受环境约束的机器人位力控制问题,将SOS理论与滑模控制理论相结合,利用Lyapunov稳定性理论设计了一种新型的CSNH位/力控制控制策略,给出了该控制策略在SOS框架下的可解性条件。大量的对比仿真结果表明,所提CSNH位/力控制对外界扰动和控制器摄动具有较强的抑制效果,使系统具有较小的轨迹跟踪误差,验证了所提控制策略的实用性、有效性及优越性。