改进ORB特征提取算法的ORB-SLAM2定位研究*

季莘翔,王宇钢,林一鸣

(辽宁工业大学机械工程与自动化学院,锦州 121001)

0 引言

伴随智能巡检机器人的广泛应用,其核心技术之一的视觉同步定位与建图(visual simultaneous localization and mapping,V-SLAM)已成为机器视觉的热点研究方向[1]。相比于激光SLAM,V-SLAM可以通过相机进行空间定位,无需人工信标和ID信息,具有体积小、性价比高、信息丰富等优势[2]。ORB-SLAM2是首个支持单目、双目和RGB-D相机的完整开源视觉SLAM方案,可以实时计算相机的位姿且能够三维建图,应用最为广泛[3]。

特征提取是决定视觉SLAM精度和效率的关键环节,目前已有SUFT、FAST和ORB等许多比较成熟的算法[4]。其中,RUBLEE等[5]结合FAST角点检测算法和BRIEF二进制特征描述算法提出了ORB算法,具有旋转不变性和提取计算速度快的优势。但其同时存在提取特征点分布不均匀问题,进而影响匹配精度和效率。因此学者基于上述问题针对传统ORB算法进行了改进研究。倪翠等[6]通过分析图片的复杂程度和分割区域个数,对各区域计算自适应的阈值,但复杂的分析和阈值计算增加了特征点提取的时间。姚晋晋等[7]通过对不同的图片灰度值检测,计算出适应不同图片的阈值算法,该算法具有更强的抗干扰能力,但耗时较长。MUR等[8]使用四叉树算法提高特征点的分布均匀度,因具有良好的旋转不变性和尺度不变性,被成功应用到ORB-SLAM2中。但文献[8]算法提取时间明显增加,特征点强行平均分配,导致产生灰度值差值小的特征点在匹配时会误匹配,从而影响定位精度。以上方法绝大部分只进行了特征点提取阶段的实验分析和验证,而缺少结合ORB-SLAM2进行轨迹定位研究,无法证实改进算法在机器人定位建图过程的应用效果。

针对上述情况,本文提出了一种改进的ORB算法。首先采用四叉树算法对图片进行分割,然后通过密度峰值聚类算法(density peaks clustering,DPC)得到各区域特征点峰值,依据结果将区域划分为高、低数量区,并对密度峰值高的区域使用四叉树多次分割,同时加入阈值middleThFAST,提高特征点灰度值差值,减少冗余特征点,提高图片特征点均匀性。最后通过数据集进行特征点提取与匹配实验验证,并将本文算法应用于ORB-SLAM2中开展了定位试验研究。

1 ORB-SLAM2结构

ORB-SLAM2由3个主要的并行线程组成:跟踪、局部建图和回环检测。跟踪线程使用ORB算法从图像中提取特征并进行匹配,定位每帧相机位姿并生成关键帧。局部建图线程运用局部BA算法优化相机位姿和特征点云。回环检测线程检测回环并通过位姿图优化消除累计漂移误差。在位姿图优化后会启动第4个线程执行全局BA算法,计算整个系统最优结构和运动结果[9]。本文采用改进的ORB算法取代ORB-SLAM2中原有的文献[8]算法,实现特征点提取和匹配,对机器人的位姿估计,并最终应用于ORB-SLAM2中进行跟踪定位。系统框架结构如图1所示。

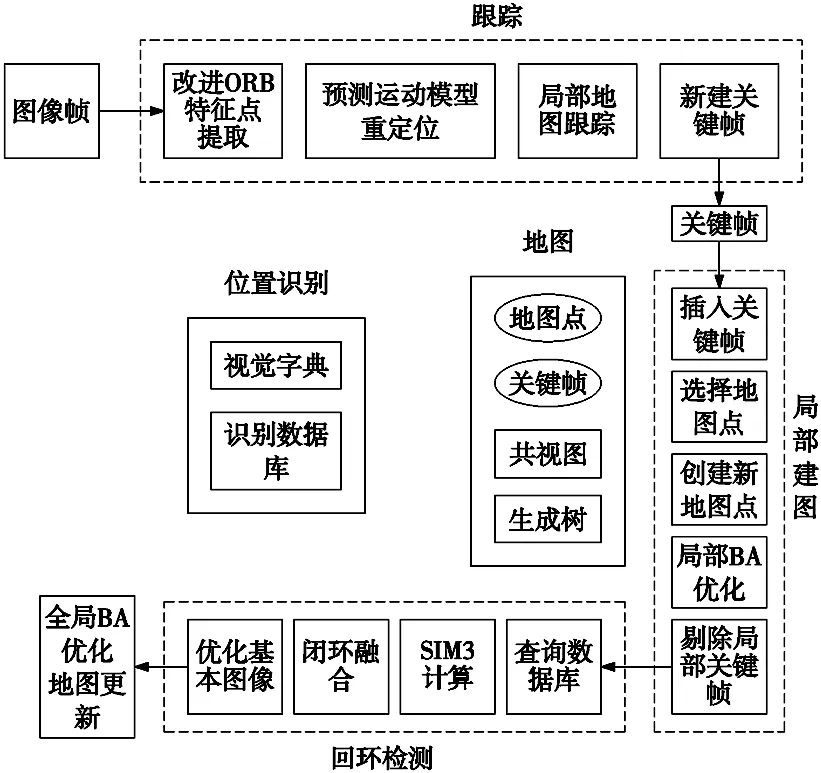
图1 ORB-SLAM2结构图

2 改进ORB算法

2.1 传统ORB算法

ORB算法包括oFAST(oriented FAST)特征点检测和rBRIEF(rotation BRIEF)描述子计算两个步骤。oFAST算法能够通过灰度质心法使特征点具有方向信息。rBRIEF算法将oFAST算法得到的方向信息,作为主方向信息,进行描述子计算,解决BRIEF算法不具备旋转不变性的缺陷[10]。

ORB算法通过比较待测像素点p与周围邻域16个像素点的灰度值差值来判断该点是否为角点。待测像素点p灰度值为I(p),设定的阈值为t,若16个像素点中有N个以上像素点的灰度值差值的绝对值大于设定的阈值,则判定为角点[11],特征点判定如式(1)所示。

(1)

式中:I(x)为范围内16个像素点中的任意一个点的灰度值,I(p)为待确定点的灰度值,t为设定的阈值。

rBRIEF算法在特征点周围选取一对的子窗口,求出各个子窗口的灰度差进行二值化,并组成二进制编码,形成特征点的描述子。将oFAST算法得到的特征点的主方向作为rBRIEF算法的主方对于任意位置坐标构造2×n矩阵,矩阵进行旋转变换,最终得到具有旋转不变性的描述子为:

Gn=(p,θ)=fn(p)|(xi,yi)∈Aθ

(2)

式中:Gn为描述子,p为待测像素点,θ为特征点主方向,fn(p)为二进制编码,(xi,yi)为任意位置坐标,Aθ为选装变换后得到的旋转矩阵。

2.2 改进ORB算法

针对传统ORB算法存在的特征点分布不均匀问题,本文通过DPC算法计算四叉树分割区域特征点数量的峰值。根据峰值将各区域划分为2个高数量区和2个低数量区,对高数量区再次使用四叉树多次分割,使特征点均匀分布在整幅图片上。在特征点提取初始阈值(iniThFAST)和最小阈值(minThFAST)中加入中间阈值(middleThFAST),缩小提取特征点阈值的跨度,进而提高特征点灰度值差值,提高图片特征点均匀性。

DPC算法基于特征点的局部密度Pi与数据点距离δi这两个数值,通过对各个数据点局部密度和距离的计算统计,构建数据的决策图以快速识别准确的簇中心[11]。该算法基于两个基本假设:①簇中心(密度峰值点)的局部密度大于围绕它的邻居的局部密度;②不同簇中心之间的距离相对较远。Pi定义如式(3)所示。

(3)

式中:Pi为点xi局部密度,dij为xi和xj之间的欧式距离,dc为截断距离。若xi>xj,则xi到局部密度最大且距离最近的特征点xj的距离δi计算方法如式(4)所示,否则距离δi计算方法如式(5)所示。

δi=minj(dij)

(4)

δi=maxj(dij)

(5)

经实验确定,当本文算法中高数量区分割次数大于3次时提取特征点分布结果不再明显变化,但运算时间会随分割次数显著增加。因此,本文将最大分割次数设定为3次。

传统ORB算法在提取时,最小阈值(minThFAST)过低会导致产生大量冗余特征点,增加运算时间,最小阈值过高,提取不到足够的特征点。因此,本文算法在iniThFAST和minThFAST中间加入middleThFAST。当在高数量区域依据iniThFAST提取特征点的数量不足时,采用middleThFAST代替minThFAST进行特征点提取。此时阈值较高,提取出的特征点灰度差值较大,提取出的冗余特征点较少,剔除时间更短。当在低数量区域以middleThFAST提取特征点时,如果满足设定值,则要比用minThFAST提取出的特征点灰度大,冗余特征点少。如果没有满足设定值,降低至minThFAST进行再次提取与剔除。middleThFAST计算方法如式(6)所示。

(6)

流程图如图2所示,算法步骤为:

图2 改进ORB算法流程图

步骤1:读取图像,设置参数iniThFAST,middleThFAST和minThFAST;分割次数i=0,imax=3;

步骤2:构建图像金字塔;

步骤3:用四叉树算法分割图片,并提取特征点,i=i+1;

步骤4:根据DPC算法得到各区域的特征点峰值划分出高、低数量区域;

步骤5:低数量区域,根据middleThFAST和minThFAST阈值提取特征点并转到步骤6;高数量区域,根据iniThFAST和middleThFAST提取特征点并转到步骤5;

步骤6:判断i是否小于等于imax,若满足转到步骤2,否则转到步骤6;

步骤7:将步骤3和步骤4的图片分割区域进行拼接,构建描述子。

3 实验与分析

实验运行环境:操作系统为VM虚拟机Ubuntu18.04LTS,CPU为Intel(R) Core(TM) i7-10875H,主频2.30 GHz,内存为8 G,开发语言为C++。

3.1 特征点提取与匹配实验

采用Mikolajczy数据集中5组图片进行特征点提取与匹配实验。bark数据集为一组内容单一且覆盖全图的图像;bike数据集为一组模糊程度不同的图像;leuven数据集为一组光照明暗不同的图像;wall数据集为一组同内容不同角度的图像;ubc数据集为一组压缩度不同的图像。

图3为3种算法在ubc数据集的部分提取结果,图中不同大小的圆和点为提取的特征点位置。由图可知,传统ORB算法提取特征点时,提取到的特征点数量有限,主要集中在树体边缘和窗框等颜色差值明显部分,在建筑墙体和树本体取的特征点却很少,分布极不均匀;本文算法提取到的特征点相比传统ORB算法和文献8算法更多,而且分布在整幅图片上。

(a) 传统ORB算法

(b) 文献[8]算法

(c) 本文算法

本文采用分布均匀度U作为特征点分布均匀性的客观评价指标,计算方法如式(7)所示[12]。

U=101log(v)

(7)

式中:v为区域统计分布向量的方差,区域统计分布向量指各区域特征点数量值形成的向量。对6组数据集的特征点提取实验结果如表1所示。

表1 特征点提取实验结果

由表1可知,针对5组不同数据集,在提取时间方面本文算法略低于传统ORB算法,但优于文献[8]算法,运行时间平均节省16.4%。在均匀性方面,由于本文算法特征点数量提取更多,针对灰度差值较大区域,特征点数量分配更多。因此本文算法在分布均匀度上性能优于传统ORB算法,略低于文献[8]算法。综上所述,3种算法对比,本文算法在提取特征点分布均匀性和运算效率综合性能更好,为实现图像特征匹配提供了良好基础。

图4为针对leuven数据集,传统ORB算法、文献[8]算法和本文算法提取的特征点进行匹配结果。从图4可以看出本文算法在不同数据集下均可有效运行,特征匹配精度较好。本文采用匹配精度M作为客观评价指标,计算方法如式(8)所示。

(a) 传统ORB算法

(b) 文献[8]算法

(c) 本文算法

M=N/N0

(8)

式中:N为通过随机抽样一致性算法匹配到的特征点数目,N0为通过最近邻算法和旋转一致性匹配到的特征点数目。

表2为5组数据集的提取特征点匹配实验结果。本文算法针对5种数据集在匹配时间和匹配精度方面均保持在较高水平,且结果稳定,表明本文算法具有较好的泛化性能。3种算法相比,在运算时间方面,相比传统ORB算法和文献[8]算法,本文算法平均用时减少9.45%。本文算法对比文献[8]算法在匹配精度方面提高了3%,与传统ORB算法相当。

3.2 ORB-SLAM2定位实验

基于TUM RBD-benchmark的2个数据集进行定位实验研究。数据集序列由高精度运动捕获系统提供,其轨迹可认为是真实轨迹,其中desk数据集长度为9.263 m,平均速度0.413 m/s;room数据集长度为15.989 m,平均速度0.334 m/s。文献[8]方法已被广泛应用于ORB-SLAM2,因此将本文方法与文献[8]方法的轨迹进行分析比较,验证文本算法在ORB-SLAM2中的实际效果。

实时性是评价ORB-SLAM2的重要指标之一,表3为每帧追踪时间均值对比结果。由表3可知,因为增加了特征点的分布均匀度和单幅图片的特征点提取效率,本文算法的每帧追踪时间比文献[8]算法平均节省12.4%,提高了ORB-SLAM2的实时性。

表3 每帧追踪时间均值对比结果 (ms)

图5为两种算法运动轨迹图,灰色虚线为数据集给出的参考轨迹,彩色实线代表估计轨迹,并通过颜色区分不同程度的定位误差。由图5a和图5c可知,文献[8]算法在大弧度转弯处有明显的偏移,是因为在速度恒定时,转弯会导致连续几帧图片中的重复部分变小,此时若存在大量灰度差值较小的特征点,会导致匹配精度下降,从而影响定位精度。本文算法如图5b和图5d所示,减小了在同一位置的定位误差,说明本文算法对定位精度有所提升。

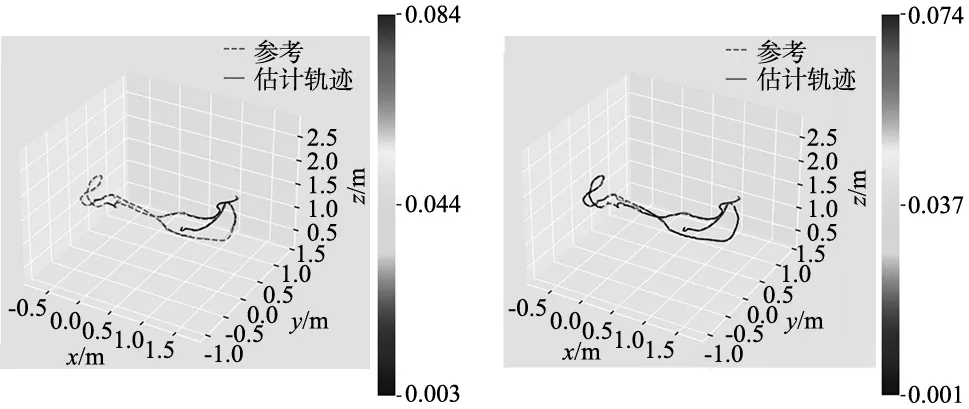
(a) 文献[8]算法运行desk数据集 (b) 本文算法运行desk数据集

(c) 文献[8]算法运行room数据集 (d) 本文算法运行room数据集

为了量化定位精度,采用绝对轨迹误差(absolute trajectory error,ATE)进行比较分析。绝对轨迹误差是估计位姿和真实位姿的直接差值,可以非常直观的反应算法精度和轨迹全局一致性[13]。ATE越小,精度越高。第i帧ATE定义如式(9)所示。

(9)

使用均方根误差(RMSE)统计ATE,计算方法如式(10)所示。

(10)

式中:Fi为第i帧的ATE,Qi为真实位姿,Pi为算法估计位姿,S为从估计位姿到真实位姿的相似旋转矩阵。

图6a～图6d分别为两种算法运行desk数据集和room数据集的绝对轨迹误差图。由图6a和图6b对比可知,对于desk数据集文献[8]算法的最大误差峰值为0.085远大于本文算法的0.045,且本文算法轨迹误差波动范围较小。对于room数据,由图6c和图6d对比可知具有相似结论。结果表明相较于文献[8]算法,本文算法绝对轨迹误差有着明显的减小,定位精度提升。

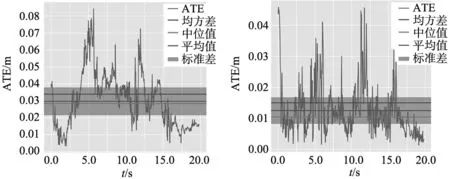
(a) 文献[8]算法运行desk数据集 (b) 本文算法运行desk数据集

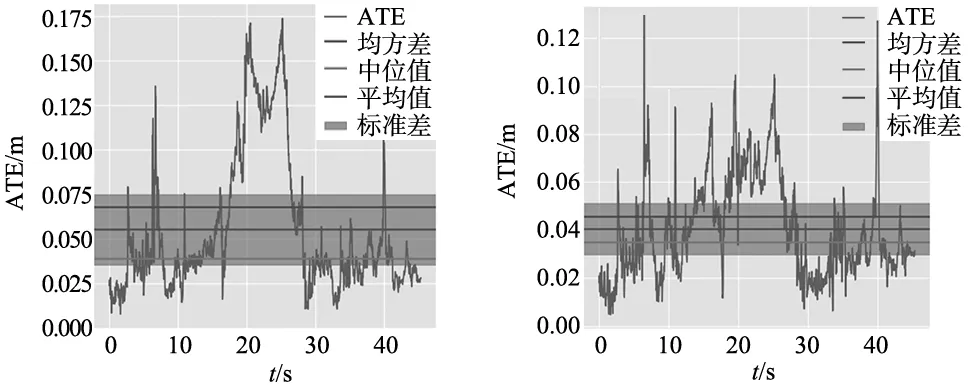
(c) 文献[8]算法运行room数据集 (d) 本文算法运行room数据集

表4为两组数据集误差对比。由表4可知,在desk数据集中,本文方法在均方根误差、中值误差和均值误差上对比文献[8]算法分别低12.57%、6.75%和17.05%;在room数据集中,在均方根误差、中值误差和均值误差上分别低19.74%、10.12%和23.14%。

表4 两组数据集误差对比 (m)

综上所述,本文算法对比文献[8]算法,在各种条件下的图片数据集中,特征点提取效率和特征点匹配精度均有提高,在室内小范围有回环数据集desk和室内大范围有回环数据集room中定位精度均有提高。

4 结束语

本文提出一种改进的ORB特征提取算法。通过DPC算法依据峰值密度划分高、低数量区域,并对高数量区域进行多次分割;同时加入middleThFAST阈值,提高特征点灰度值差值,提高特征点分布均匀性。

在Mikolajczy数据集下,本文算法相比传统ORB算法在均匀度方面提高了12.45%,匹配效率提高9.45%,有效地解决了提取特征点分布不均匀问题。同时,将本文算法应用于ORB-SLAM2,实现了机器人运动定位精度和实时性的提升。通过TUM数据集验证得出,在定位精度方面平均提高了15.83%,每帧追踪时间平均减少12.4%。实验结果表明本文提出的改进ORB算法能够有效提升机器人的即时定位精度,可应用于机器人的路径规划和导航。