基于超局部模型的永磁同步电机预测控制*

吴艳娟,林峻山,王云亮

(天津理工大学a.电气工程与自动化学院;b.天津市复杂系统控制理论及应用重点实验室;c.天津市新能源电力变换传输与智能控制重点实验室,天津 300384)

0 引言

近年来,电动汽车、机器人等领域发展迅速。表贴式永磁同步电机(SPMSM)因为具有较高的功率密度、动态性能优秀等优点,在这些领域中得到了广泛的应用[1]。目前SPMSM驱动系统使用的控制策略主要包括磁场定向控制,直接扭矩控制和模型预测控制[2-4]。

MPC因具有多变量约束、动态性能好和清晰的物理概念等优点被广泛使用[5]。MPC需要精确的电机模型和电机参数进行预测控制。如果控制系统中的电机参数发生变化,MPC的性能将会变差,最终对电机驱动系统产生负面影响[6]。

因此为了提高MPC在模型失配情况下的鲁棒性,提出了很多解决方案。其中无模型控制的方法不依赖于电机参数,已经被应用于PMSM驱动系统的控制中[7-11]。LIN等[7]提出了一种基于电流差的无模型预测电流控制(model-free predictive current control,MFPCC)方法,利用之前存储的不同电压矢量引起的电流变化量预测未来的电流值。该方法计算量小,但是会存在电流差更新停滞的问题。WU等[8]则是采用了一种多电流差更新的方法。在这种方法中,电压矢量引起的电流差更新的同时,与该矢量方向相反的电压矢量对应的电流差也被更新,这显著提高了电流差更新频率,但是仍然存在电流差更新停滞的问题。MA等[9]中首先分析了电流梯度与施加的电压矢量之间的关系。然后,通过进一步分析施加的电压矢量与其他矢量之间的关系,可以推导出一个控制周期内所有电压矢量的电流梯度。因此,通过保持所有当前梯度信息的最新状态,可以有效地解决传统MFPCC中存在的停滞问题。由于ESO具有较强的扰动估计和简单计算能力,ZHANG等[10]提出了一种基于超局部模型的带有ESO的新型MFPCC。赵凯辉等[11]提出了使用结合超局部模型和滑膜观测器的新型MFPCC。GAO等[12]提出了使用超局部模型的模型预测速度控制,通过使用扩张状态观测器估计模型中的未知参数,在电机参数失配时也有较好的表现。

为实现永磁同步电机参数变化的鲁棒控制,提出一种改进的基于超局部模型的无模型电流预测控制方法。所提方法使用自适应径向基函数神经网络(adaptive radial basis function neural network,ARBFNN)观测器来估计超局部模型中的未知参数。在电机参数失配的情况下,稳态性能和动态性能均优于传统的存在参数的有限控制集模型预测电流控制(finite control set model predictive current control,FCS-MPCC)方法。

1 传统FCS-MPCC方法

忽略铁磁材料的饱和效应等次要因素的影响,SPMSM在d-q旋转坐标系下的数学模型可以表示为:

(1)

式中:ud、uq分别代表d、q轴电压,id、iq分别代表d、q轴电流,Rs为定子电阻,Ls为定子电感,ωe为电角速度,ψf代表转子磁链。

在FCS-MPCC控制方式中,需要采用离散模型。采用前向欧拉法对电机的数学模型离散化,假设采样时间为Ts,当前时间为k,可得到:

(2)

式中:id(k)、iq(k+1)分别代表时间k处d、q轴定子电流,id(k+1)、iq(k+1)分别为k+1时刻预测的d、q轴定子电流。

在采用两电平电压源逆变器的驱动系统中,d-q旋转坐标系中的定子电压可以描述为:

(3)

式中:VDC是直流输入电压,θ为转子角,Sa、Sb、Sc分别代表逆变器3个桥臂的开关状态,开关状态有(000、001、010、011、100、101、110)。

FCS-MPCC的代价函数一般为:

(4)

传统FCS-MPCC方法中将7中开关状态代入式(3)中求出对应的ud、uq分别代入式(2)中计算出电流预测值,然后将电流预测值代入式(4),采用使代价函数最小的电压矢量。

2 无模型预测控制

2.1 超局部模型

在本文中采用单输入单输出超局部模型来替代SPMSM的数学模型。超局部模型不使用任何电机参数。一阶超局部模型可以表示为:

(5)

式中:y为系统输出变量,x为状态变量,u为输入变量,α、F分别为自定义系数和系统的未知部分。

将SPMSM的数学模型代入一阶超局部模型,则SPMSM在d、q旋转坐标系中的一阶超局部模型可以表示为:

(6)

式中:Fd、Fq为未知参数。

2.2 自适应径向基函数神经网络观测器

为了估计未知参数Fd、Fq,本文设计了自适应径向基函数神经网络观测器(ARBFNN)。定义F的逼近函数为:

F=φ*TP+ε*

(7)

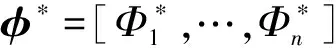
理想的神经网络权值不容易求得,可采用下式对F进行逼近:

(8)

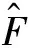
(9)

将上一次电流估计误差作为输入,自适应径向基函数神经网络观测器定义为:

(10)

观测器的自适应律设计为:

(11)

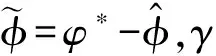
稳定性证明:

构造Lyapunov函数为:

(12)

对式(12)求导:

(13)

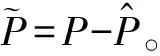
将式(11)代入式(13)得:

(14)

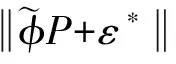
(15)

从t=0到T,对式(15)积分得:

(16)

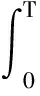
(17)

当t→∞时,e→0,故所提出的ARBFFNN观测器满足稳定性准则,系统能够收敛。

对式(10)进行离散化:

(18)

2.3 方法实施步骤

所提出的采用自适应径向基函数的有限控制集无模型预测电流控制(FCS-MPCC-MFPCC)方法的总体控制过程可以总结为以下步骤:

步骤1:测量定子电流、转子位置、转速;

步骤2:将实际电流与估计电流的误差作为输入通过ARBFNN观测器估计未知参数F,同时调整神经网络的权重;

步骤3:将7种开关状态代入式(2)中,计算出对应的ud、uq;

步骤4:使用观测器估计出的未知参数,根据式(18)计算出7种不同的开关状态所对应的电流预测值;

步骤5:使用式(4)所示的代价函数选择最佳的开关状态输出。

3 仿真实验

为了验证本文中所提出的方法,在MATLAB/Simulink仿真环境中对传统FCS-MPCC和所提出的FCS-MFPCC-ARBFNN进行了仿真对比。本文中提出的FCS-MFPCC-ARBFNN的控制系统结构如图1所示。在本文中采用自适应径向基函数神经网络分别对未知参数Fd、Fq进行估计,其中每层的神经元个数分别为1、2、1。初始权重设计为0～1之间的随机数。为了保证系统的动态性能和鲁棒性,参数m被设置为19 000,电机的参数和其他仿真中的参数在表1中给出。仿真开始时,设置电机初始速度为500 r/min,采用d轴参考电流为0的控制方式,电机空载启动。在0.3 s时给定转速增大到1000 r/min,在0.6 s时负载转矩增加到20 N·m,其中控制系统的采样频率为10 kHz。

表1 仿真及实验参数

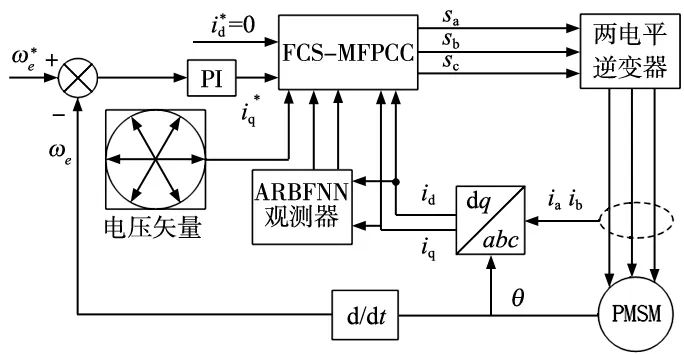
图1 FCS-MFPCC-ARBFNN的控制系统结构框图

传统FCS-MPCC方法仿真结果如图2所示,其中图2a为转速响应,图2b和图2c分别为d、q轴电流响应。所提出的FCS-MFPCC-ARBFNN的仿真结果如图3所示,其中图3a为转速响应,图3b、图3c分别为d、q轴电流响应。

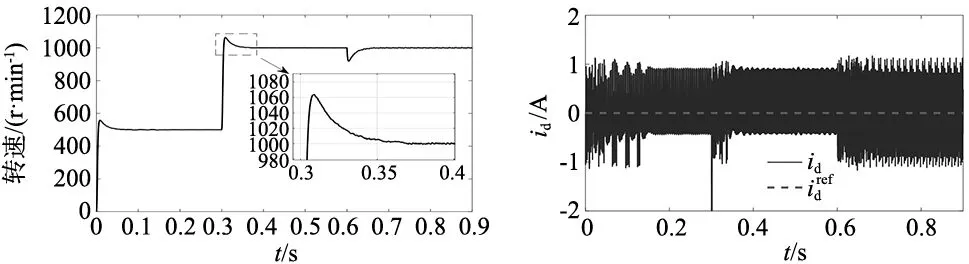
(a) 转速响应 (b) d轴电流

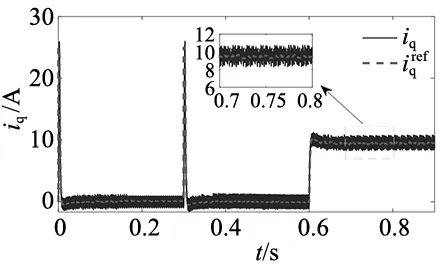
(c) q轴电流

(a) 转速响应 (b) d轴电流

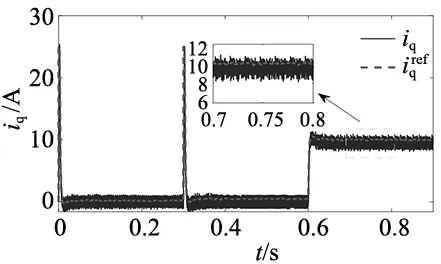
(c) q轴电流

从图3a中可以看出,在精确的电机参数下,所提出的方法在空载启动时能快速达到给定转速,并且在给定转速突变和突增负载时也能够快速到达指定转速。由图2a、图3a的对比可见,两种方法具有相似的响应速度,所提出的方法转速超调量跟传统方法也几乎相等。从图2b、图2c和图3b、图3c中可以看出,在稳态时两种方法的d、q轴电流的跟踪误差也较为相似。仿真结果表明,所提出的方法在精确的电机参数下具有和传统方法相似的性能。

为了对比在参数发生失配时两种方法的性能,将控制器中的电机磁链和电阻设置为电机中实际值的2倍,电感设置为实际值的0.5倍,其他测试条件不变。

图4和图5分别为PMSM发生参数失配时,FCS-MPC和FCS-MFPCC-ARBFNN的仿真结果。其中,图4a和图5a为转速响应;图4b、图4c和图5b、图5c为d、q轴参考电流和实际电流。从仿真结果中可以看出,在这种情况下,不匹配的参数显然对传统的FCS-MPCC有较大的影响。从仿真结果可以看出在传统的FCS-MPCC中q轴电流已经不能准确地跟踪参考值,存在一些明显的偏移。相反,在FCS-MFPCC-ARBFNN中消除了q轴电流的稳态跟踪误差,对电机参数变化表现出很强的鲁棒性。此外,传统方法中的d轴电流跟踪误差也更大。同时,从图4a和图5a中可以看出,传统方法的超调更大。仿真结果证实,所提出的方法具有较好的稳态性能和动态性能。

(a) 转速响应 (b) d轴电流

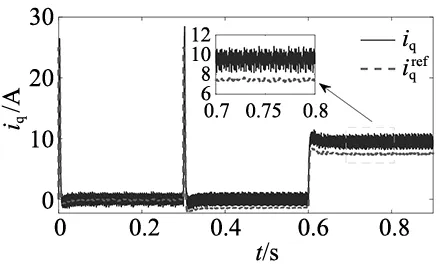
(c) q轴电流

(a) 转速响应 (b) d轴电流

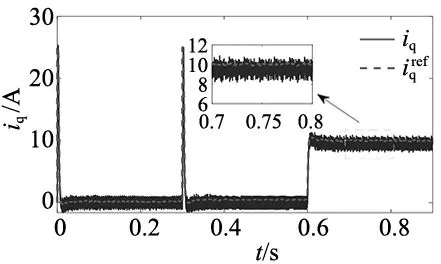
(c) q轴电流

4 实验验证

为了进一步验证所提方法的实际控制效果,在RT-LAB实时仿真平台上进行了实时仿真实验,图6为采用的实验平台。实验中所用参数与simulink仿真中的参数一致。

图6 RT-LAB实验平台

在电机参数发生变化时将所提出的方法与传统FCS-MPCC进行对比,令控制器中给定电感为实际值的0.5倍,磁链为实际值的2.5倍,电阻为实际值的2倍。其他条件不变的情况下两种控制方法的性能分别如图7和图8所示。

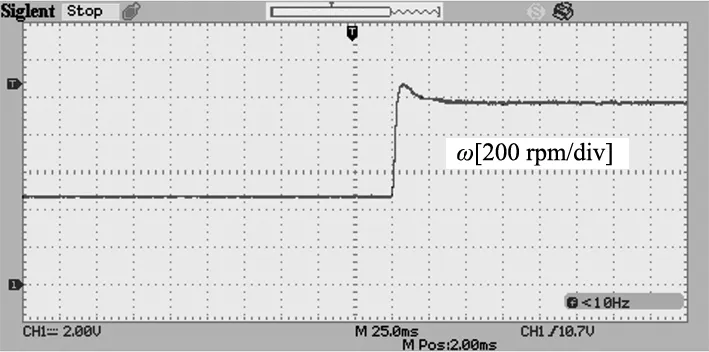
(a) 转速响应

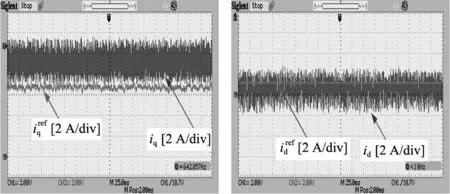
(b) q轴电流 (c) d轴电流

(a) 转速响应

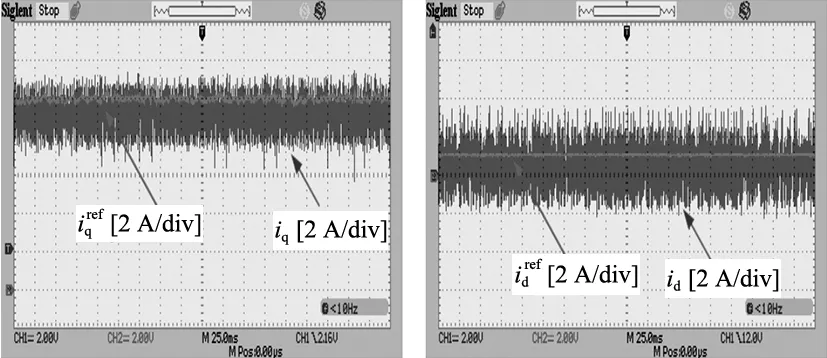
(b) q轴电流 (c) d轴电流

从结果中可以看出在参数失配的情况下两种方法有相似的响应时间。然而,传统方法的转速从500 r/min变为1000 r/min时最大超调量为70,而所提出的方法转速最大超调为55,这表明所提出的方法的动态性能要更好。同时,在稳态运行时,虽然两者的d轴电流都能跟踪上参考电流并且跟踪误差也相似,但是传统方法的q轴电流对给定值的跟踪出现了明显的偏差。结果表明,本文所提方法在该种参数失配情况下的性能更好。

5 结论

针对SPMSM模型预测控制系统在电机参数变化引起的电机鲁棒性和控制性能下降的问题,本文采用基于超局部模型的无模型预测电流控制方法,设计了RBFNN观测器对控制系统中的未知部分进行实时准确的估计,通过电流误差大小实时调整RBFNN观测器的权重参数,并且通过李雅普诺夫稳定性定理进行了稳定性证明。通过与传统FCS-MPCC方法和FCS-MFPCC-ARBFNN方法的对比,可知,所提出的方法在参数准确时具有与传统方法相似的性能。然而,在电机参数失配的情况下,采用所提方法时,电机转速的超调量更小,d、q轴电流与给定值之间的误差也更小,系统的动态性能和稳态性能均有提升。仿真和实验结果验证了所提方法在保持传统方法优势的同时具有良好的参数鲁棒性。