基于四阶S曲线加减速的NURBS曲线插补算法

贺 涛,杨煜俊,汪晓松

(广东工业大学机电工程学院,广州 510006)

0 引言

随着现代数控加工技术对产品质量和加工效率的追求,面向高速高精加工的NURBS曲线插补技术变得越来越重要。在NURBS曲线插补中,进给速度的变化是机床产生振动和影响加工质量的重要原因之一。LIN等[1]采用五段式S曲线加减速控制算法进行加减速插补,虽达到加减速度控制要求,但仅适用于不需要匀加速段就能达到最大进给速度的情况;潘海鸿等[2]给出七段S型曲线加减速控制中可能出现的17种速度曲线变化类型,研究适用于前瞻控制的七段式S型曲线加减速控制算法;于金刚等[3]提出一种基于加加速度控制的加减速控制方法,采用限制加加速值,并利用滤波器对加速度进行光滑处理来减少加工中由于加加速突变而产生的机床振动;LEE等[4]提出了一种离线进给率调度方法,该方法考虑了弦误差、加速度和加加速度限制所施加的约束,但是与时间最优和S曲线加减速相比,用这种方法获得的加速度函数是不连续的。杨亮亮等[5]将速度和位移方程转换为一元高次方程,其求解复杂,增加了计算负担;WANG等[6]结合几何和动态约束计算曲线进给速度,根据进给速度关键区域将曲线分段,再由切向加速度和加加速度生成一个自适应的平滑S形进给速度曲线;李志杰等[7]提出一种加加速度连续的S型加减速规划算法,其加速度曲线由三角函数与直线连接组成,能得到平滑连续的加速度与速度曲线,与纯三角函数加减速曲线相比可控性更强,但是加减速模式规划方法较为复杂;NGUYEN等[8]提出任意阶次多项式加减速控制的算法,并推导出三阶、四阶和五阶S曲线加减速控制的模型;赵翔宇等[9]研究了三次S曲线加减速,对加加速度节点突变问题有一定程度上的优化,但是还可以进一步完善。穆海华、朱其新等[10-11]研究了四阶S曲线加减速算法,每个时间点的计算都要经过多次的比较和修正,算法效率不高,计算量较大;周黎等[12]对四阶S曲线加减速算法优化改进,根据各种极限情况下的位移值对目标位移量进行分类,可以直接确定对应轨迹的相关时间量,降低了算法的计算量。

上述对四阶S曲线加减速算法的研究中,均未考虑非对称四阶S曲线模型,且无法适应NURBS曲线插补中可能出现的较短弧长。为此,提出一种基于四阶S曲线加减速的NURBS曲线插补算法,考虑四阶S曲线所有可能出现的速度模型,对其进行判别分类,并采用二分法寻找较短弧长的实际最大速度,最后通过仿真验证了算法的有效性。

1 NURBS曲线速度规划预处理

1.1 NURBS曲线公式及弧长计算

NURBS曲线采用分段有理多项式矢函数[13]:

(1)

式中:u为NURBS曲线参数,di为控制顶点(i=0,1,…,n),ωi为控制顶点的权因子Ni,k(u)为第i个k次B样条基函数。

NURBS曲线的曲率计算式[14]:

(2)

式中:C′(u)和C′′(u)分别是NURBS曲线的一阶导数和二阶导数。

规划进给速度还需计算NURBS曲线的弧长,在参数[us,ue]曲线弧长为:

(3)

式(3)无法精确求解,因此可利用数值积分中的辛普森法则[15]近似求解:

(4)

为了保证计算精度,[us,ue]不能过大,应用完全辛普森规则将[us,ue]划分为2个相等的区间,即[us,(us+ue)/2]和[(us+ue)/2,ue],给定精度ε进行校验:

(5)

通过不断二分区间直到满足上述精度要求,将所有子区间的弧长累计,即可得到对应精度的弧长。

1.2 速度规划预处理

为控制速度平稳光滑不超限,并减小插补过程中产生的误差,选取自适应速度作为后续速度规划的最大速度上限。首先选取NURBS曲线上曲率大于曲率阈值的点称为候选点,具有局部最大曲率的候选点作为临界点,临界点把NURBS曲线分割成若干段;然后根据弓高误差差、法向加速度和加加速度确定曲率半径阈值[4]。

(6)

式中:Ts为插补周期,δ为最大弓高误差,vmax为最大进给速度,An为最大法向加速度,Jn为最大加加速度。

任意点处速度值应满足最大弓高误差δ、最大进给速度vmax、最大法向加速度An以及最大加加速度Jn的约束。

(7)

2 四阶S曲线加减速模型

2.1 四阶S曲线加减速原理分析

图1为标准的对称四阶S曲线加减速的位移、速度、加速度、加加速度和加加速度的斜率的曲线图。由图可知,该轨迹规划可由4段时间唯一确定。

图1 标准的对称四阶S曲线加减速过程

(1)最大加加速度的斜率时间段Ts(图中部分Ⅰ);

(2)最大加加速度jmax时间段Tj(图中部分Ⅱ);

(3)最大加速度amax时间段Ta(图中部分Ⅲ);

(4)最大速度vmax时间段Tv(图中部分Ⅳ):

在确定了以上4个时间段之后,也就可以确定算法实现过程中所需每一段的时间节点ti(i=1,2,…,15)。假设轨迹规划数据的生成都是通过数字积分的形式进行的,即速度三阶导数的积分为加加速度,加加速度的积分为加速度,加速度的积分为速度,速度的积分为位移[10],可描述为:

(8)

式中:j0、a0、v0和s0分别为加加速度、加速度、速度和位移的初始值,d(t)、j(t)、a(t)、v(t)和s(t)分别为加加速度的斜率、加加速度、加速度、速度和位移在时间t的实际值。

2.2 四阶S曲线加减速曲线分类

四阶S曲线加减速曲线存在非对称的情况,即加速阶段和减速阶段是非对称的,因此将四阶S曲线加减速曲线分加速阶段、匀速阶段、减速阶段3个阶段分别进行讨论。

根据给定的系统参数和轨迹参数求解各段时间。先考虑匀速阶段存在,即实际速度能达到最大限制进给速度,再对加速阶段和减速阶段判别,根据各段时间是否不为0进行判别,即判断速度、加速度和加加速度是否达到最大值,再考虑匀速阶段不存在的情况,最后对所有情况进行分类。具体实施步骤为:

步骤1:对加速阶段判别。判别条件:最大速度vmax、最大加速度amax、最大加加速jmax、最大加加速度斜率dmax、初速度vs。

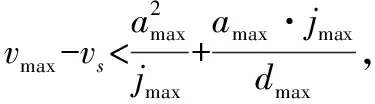
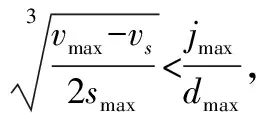
(a) 类型1 (b) 类型2 (c) 类型3

(9)

(10)

(11)

步骤2:对减速阶段判别。判别条件最大速度vmax、最小加速度amin、最小加加速jmin、最大加加速度斜率dmax、末速度ve。判别方法与加速阶段判别相同,其减速阶段3种类型如图3所示。

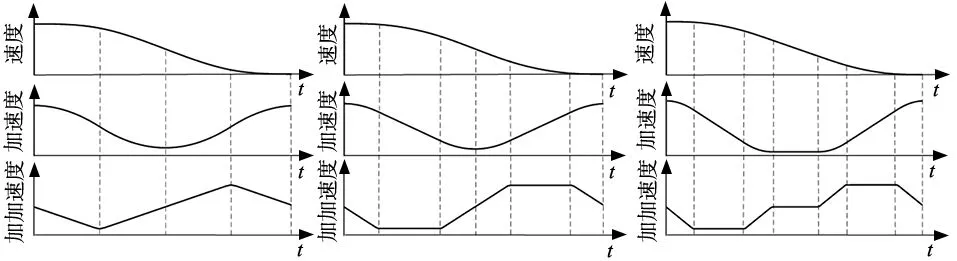
(a) 类型1 (b) 类型2 (c) 类型3

步骤3:对匀速阶段时间进行计算。

(12)

式中:sa为加速阶段位移长度,sd为加速阶段位移长度,sa、sd由式(8)计算,s为总位移长度。

当匀速阶段时间Tv>0,此时实际速度可以达到最大限制进给速度,计算结束;否则不存在匀速阶段,Tv=0,步骤1、步骤2的计算结果不成立,需计算实际达到的最大速度,跳转步骤4。

步骤4:判断最大实际速度是否是起始速度或末速度。计算只需一个加速阶段或减速初速度到末速度的临界位移sm,即实际最大加加速度为jmax,Ts=jmax/dmax,且Tj、Ta、Tv都为0。根据式(8)计算sm,然后与实际位移s比较。

(1)当s≤sm且ve≥vs,则最大速度vmax=ve,跳转步骤1;

(2)当s>sm且vs>ve,则最大速度vmax=vs,跳转步骤2;

(3)两者都不成立则跳转步骤5。

步骤5:采用二分法重新计算在给定条件下所能达到的实际最大速度。

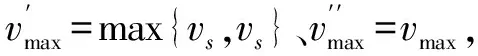
(2)根据步骤1、步骤2的时间和式(8)分别计算加速阶段的位移的sa和减速阶段的位移sd。

四阶S型曲线有加速阶段、匀速阶段、减速阶段,以此将四阶S型曲线分成3类:

(1)长块:包含加速、匀速和减速3个阶段。加速阶段有3种情况,匀速阶段存在,减速阶段有3种情况,所有长块有9种类型。

(2)中块:包含加速、匀速和减速其中2个阶段。加速阶段和减速阶段各有3种情况,匀速阶段有存在或不存在2种情况,所有中块有15种类型。

(3)短块:只包含加速、匀速和减速其中1个阶段。其为加速阶段有3种类型,其为匀速阶段有1种类型,其为减速阶段有3种类型,所有短块有7种类型。

综上所述,四阶S型曲线总共有31种速度类型。各NURBS曲线段按照对应的四阶S曲线速度类型完成曲线插补。

3 仿真结果与分析

3.1 算法有效性验证对比

为验证本文所提算法的性能,使用MATLAB软件编制程序,对曲线速度规划进行验证。以图4所示3次NURBS曲线为例,其特征参数和测试参数分别如表1和表2所示。

表1 NURBS曲线的特征参数

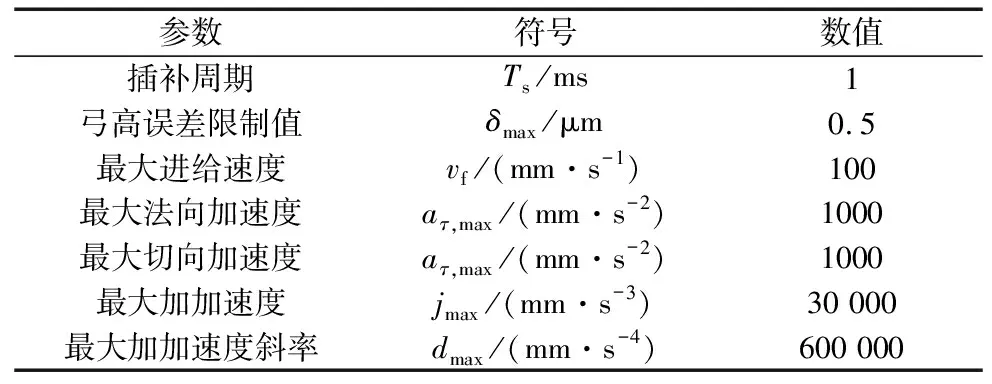
表2 NURBS曲线的测试参数

在相同限制条件下,分别对三阶S曲线加减速控制的NURBS曲线插补算法和本文提出的算法进行仿真。图5为四阶S曲线加减速规划和三阶S曲线加减速规划生成的进给速度曲线对比图。

图4 “∞”形轨迹 图5 进给速度曲线

由图6可知,三阶S曲线加减速规划生成的加速度曲线连续但不平滑,而四阶S曲线加减速规划生成的加速度曲线连续且平滑。由图7可知,三阶S曲线加减速规划生成的加加速度曲线是突变的,而四阶S曲线加减速规划生成的是加加速度连续的曲线。

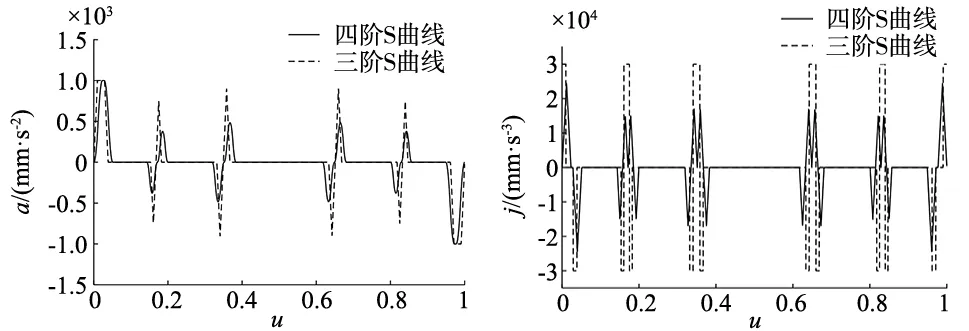
图6 加速度曲线 图7 加加速度曲线

3.2 复杂曲率情况下算法有效性验证

蝴蝶形三次NURBS曲线相比于“∞”形三次NURBS曲线,曲率更加复杂、有较多的大曲率区域,能有效验证本文所提出算法的有效性。几何模型和控制点如图8所示,曲线的特征参数参考文献[16],测试参数见表2。

插补算法加工蝴蝶形曲线得到的进给速度曲线和加速度曲线如图9和图10所示,在复杂曲率情况下,该算法依然具有有效性,保证速度、加速度不超过系统限制值。由图11弓高误差曲线所示可知,在整个加工过程,弓高误差不超过CNC系统的限制,最大弓高误差为1.35×10-4mm,平均弓高误差5.21×10-5mm。

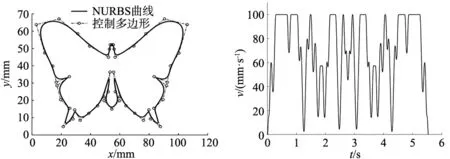
图8 蝴蝶形轨迹 图9 进给速度曲线

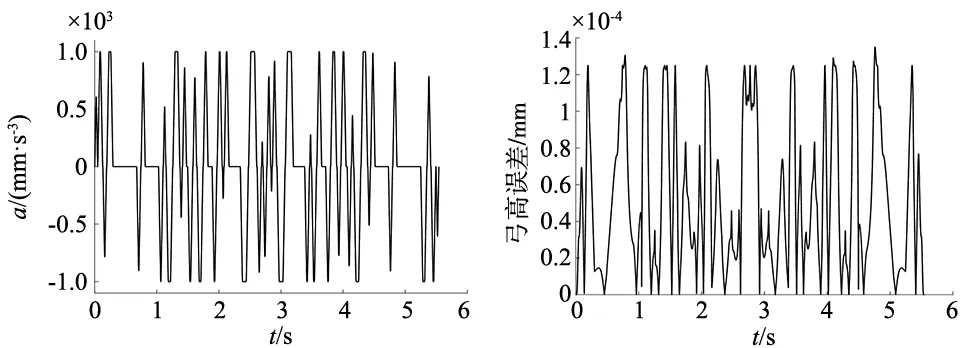
图10 加速度曲线 图11 弓高误差曲线

4 结论

为减小NURBS曲线插补在运动过程中产生的振动和冲击,提出基于四阶S曲线加减速的NURBS曲线插补算法。针对不同弧长的曲线段,分析速度、加速度、加加速度、加加速度斜率及曲线长度之间的关系;计算各阶段的时间;并采用二分法寻找较短弧长的实际最大速度。最后规划出31种速度曲线类型来自适应NURBS曲线插补。

与三阶S曲线加减速控制的NURBS曲线插补算法相比,四阶S曲线加减速控制的NURBS曲线插补算法能减低各种突变,保证插补全过程中加速度光滑、加加速度连续无突变,同时能满足复杂曲率的NURBS曲线插补。