Jerk曲线连续的改进S型加减速算法研究*

王盈余,管声启,于资江

(西安工程大学机电工程学院,西安 710048)

0 引言

在现代运动控制技术中,运动平台是不可或缺的基础实验设备。目前,高平稳性、高柔性的精密运动平台已经成为微型装配、半导体光刻、精密测量等等应用的基础,其各项指标也是衡量我国科学技术发展的一个重要标志[1-2]。对于开环的运动平台控制系统,其运动精度和加减速控制算法的好坏息息相关,通过加减速控制算法避免在运动平台启动和停止时发生冲击以及震荡,从而可提高运动平台的运动精度。因此,加减速算法的性能对于运动平台的精度是至关重要的[3]。

传统S型加减速算法也是比较常用的一种加减速控制算法,但其Jerk曲线存在突变,加速度曲线不光滑[4]。针对S型加减速算法,李哲等[5]将S型加减速算法应用在3D打印机中,把传统的7段S型加减速算法改进为5段加减速算法,有效的减少了打印过程中所存在的柔性冲击,但缺少了速度衔接点处的分析;赵翔宇等[6]提出了基于三次S曲线的加减速算法,简化了计算量,但是其匀速阶段的开始和结束阶段还是存在阶跃突变;李金良等[7]在四自由度机器人应用中提出了一种加减速控制算法,为进一步对冲压机器人进行相关动力学分析和参数优化提供参考,但是其加加速度曲线并不连续,还是存在突变;游达章等[8]提出了一种新的四次S型加减速控制算法,有效的减少了加工时间,降低了柔性冲击,但是其将传统的七段S型加减速扩充至11段,计算繁琐复杂,不适合在内存有限的嵌入式系统应用。

综上所述,本文以正弦函数为基础,构造Jerk曲线,应用切夫雪比多项式逼近正弦函数,进而获得完整的加减速算法,并根据基础的方程进一步推导出各阶段具体的时间规划,给出针对各种情况的具体速度规划,最后通过仿真验证了本文所改进算法的有效性。

1 改进S型加减速Jerk曲线的构造

三角函数具有良好的柔性度,在本文的改进S型加减速算法中,将正弦曲线引入加减速算法的Jerk曲线中,其加速度函数为:

(1)

式中:T为加速度加速时间,式(1)在t=T/2处取得最大加加速度值Jmax。

但是由于嵌入式系统内存有限中,对于三角函数的计算比较复杂,不适合满足实时的计算的要求,所以,本文采用切比雪夫多项式,对于正弦函数进行逼近,以此来减少嵌入式系统的运算量。

若令:

(2)

将式(2)代入式(1),可得:

j(x)=-Jmaxsin(πx)

(3)

此时使用切夫雪比多项式对sin(πx)进行逼近,且阶数取至4阶,可得到:

(4)

为了使加加速阶段的Jerk曲线更具有对称性,对上式关于t=T/2对称,可得到:

(5)

将式(4)和式(5)相加后便可得到[0,T]区间内的Jerk曲线方程:

(6)

式中:k为待定系数,并且在[0,T],满足j(t)≤Jmax,得到的Jerk曲线如图1所示。由于在t=T/2处时,取得最大加加速度Jmax,由此可得出待定系数|k|=4Jmax[9]。

图1 Jerk曲线图

2 改进S型加减速算法

将通过切比雪夫多项式逼近的正弦曲线引入Jerk曲线,采用类似于传统S型加减速的七段控制特点,可得到本文中所提出的改进后的加减速曲线的加速度方程、速度方程和位移方程的七段表达式。

Jerk曲线方程:

(7)

加速度曲线方程:

(8)

速度曲线方程:

(9)

位移曲线方程:

(10)

式中:vs是电机运行的初始速度,ve是电机运行的末速度,vm是电机运行的最大速度,am为最大加速度,dm为最大减速度,vi(i=1,2,3,4,5,6)是本文提出的改进算法每个阶段的初始速度,si(i=1,2,3,4,5,6,7)是每个阶段的初始位置,τi(i=1,2,3,4,5,6,7)是每个阶段初始时间为零的局部时间,Ti(i=1,2,3,4,5,6,7)为每个阶段运行时的总时间。

在得出改进S型加减速的加加速度、加速度、速度和位移的曲线方程后,就需要根据不同的运动参数,做出不同的加减速规划,总的规划流程如图2所示。

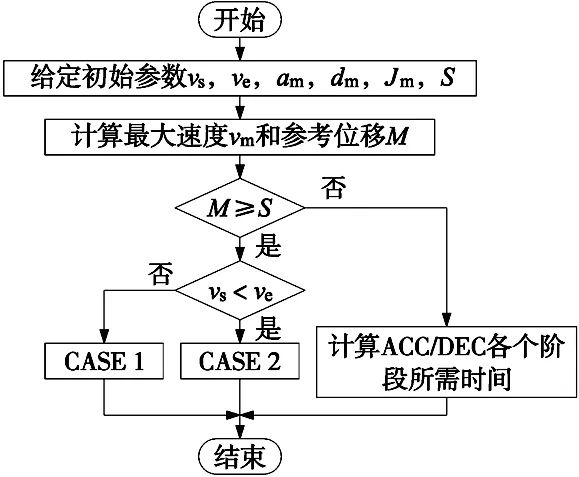
图2 改进S型加减速算法规划流程图

根据改进的S型加减速曲线可知,在加速度段,必然存在一个加速度增加段和一个加速度递减段,且两个过程所需时间相同。同时,在减速度过程中,同样存在一个递增的减速段和一个递减的减速段,其所需时间也是相同的。由此,可根据是否可以达到最大速度vm以及最大速度的大小推断出加速段和减速段中各个阶段所需的具体时间。也可根据是否存在匀速段的位移,判断出是否存在匀速段。

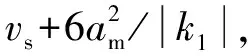
(11)

(12)

(13)

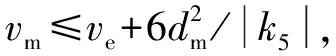
(14)

根据上述原理,计算出了加速阶段和减速阶段的具体的时间规划。由此,便可计算出不包含匀速阶段的参考位移M。

(15)

假设实际位移为S,当S≥M时,则存在一个匀速阶段,匀速阶段时间可由下式推出:

T4=(S-M)/vm

(16)

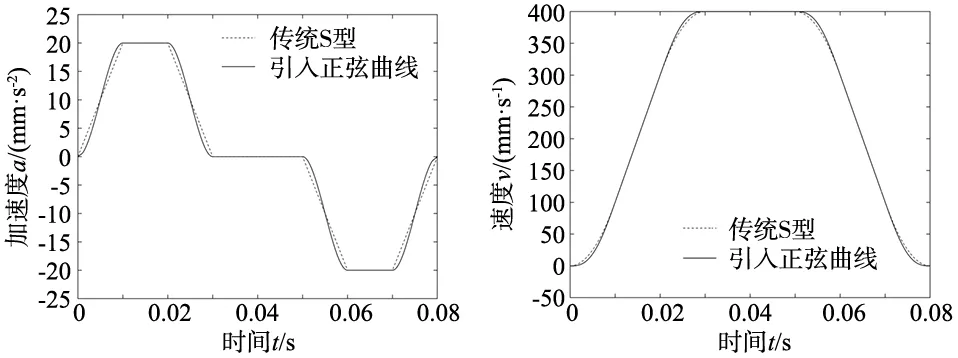
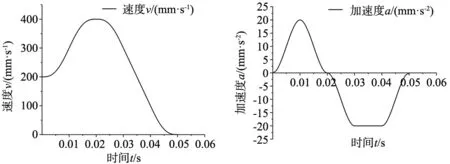
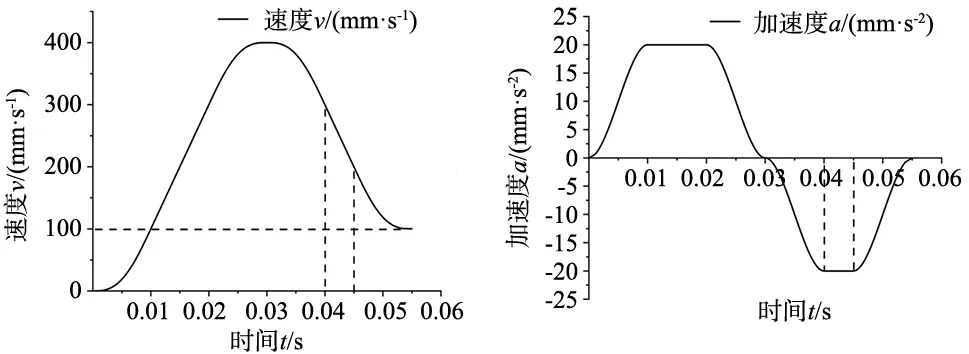
如果S

(1)CASE1:此时ve≤vs

(17)

若实际位移S>M1&S≤M,则必然存在匀加速阶段,在该情况下每个阶段所需的具体时间为:

(18)

最大速度vm可由式(15)和式(18)解出,最大速度公式为:

(19)

当|S-M1|

(20)

最大速度vm可通过式(19)解出,方法同上,此时最大速度vm为:

(21)

当S

(22)

在该情况下,由于实际位移S过小,最大加速度将随实际位移S发生改变:

(23)

(2)CASE2:此时vs

(24)

与CASE1同理,将实际位移S与参考位移M2大小进行对比,分3种情况讨论,便可计算得出在每种情况下各个阶段所需具体时间,并可求解出在实际位移不足情况下,在当前位移下自由加速所能到达的最大速度vm,由此便可完成该情况下的加减速算法规划。

3 改进“S”加减速算法仿真分析

在采用本文所改进的加减速算法进行运动控制时,需根据所应用的实际情况,给出确定的运动控制参数。本文通过MATLAB编程环境,对不同初始参数的加减速曲线进行了仿真。

为了比较本所设设计算法相对于传统S型加减速算法的优势,设计了以下参数下的对比实验:vs=0 mm/s,ve=0 mm/s,am=20 mm/s2,dm=20 mm/s2,Jmax=3 mm/s3,实际位移S=16 mm。

在该实验中,存在匀速阶段、匀加速阶段以及匀减速阶段。其速度、加速度、加加速度曲线如图3所示。

(a) Jerk曲线

(b) 加速度曲线 (c) 速度曲线

通过图3可知,在该仿真参数下,传统S型加减速加加速度曲线存在阶跃变化,会导致在加加速度转换点出现柔性冲击,造成电机运行不稳定,影响高精度运动平台的运动精度以及平稳性。并且传统S型加减速加速度曲线不光滑,限制了高精度运动平台的柔性控制。本文所改进的加减速算法加加速度曲线连续,加速度曲线光滑,速度曲线在加加速阶段、加减速阶段、减加速阶段、减减速阶段相对于传统S型曲线更加光滑,进而提高了高精度运动平台的控制稳定性。

在根据本文提出的加减速控制算法进行运动控制时,还需根据初始条件,计算出加减速各个阶段具体的时间规划。根据算法特性,给出了4组比较有代表性的参数,进行仿真验证。为了使验证具有可比性,在4组仿真实验中,最大加加速度Jmax=3 mm/s3,最大加速度am=20 mm/s2,最大减速度为dm=20 mm/s2。

(1)设定初始参数为:vs=200 mm/s,ve=0 mm/s,S=12 mm,在该参数下,实际位移|S-M1|

(a) 速度曲线图 (b) 加速度曲线图

(2)设定初始参数为:vs=100 mm/s,ve=0 mm/s,S=12.25 mm,在该参数下,实际位移S>M1,符合CASE1条件,所以此时的速度规划中存在匀加速阶段,其加减速仿真曲线如图5所示。

(a) 速度曲线图 (b) 加速度曲线图

(3)设定初始参数为:vs=0 mm/s,ve=200 mm/s,S=12 mm,在该参数下,实际位移|S-M2|

(a) 速度曲线图 (b) 加速度曲线图

(4)设定初始参数为:vs=0 mm/s,ve=100 mm/s,S=12.25 mm。在该参数下,实际位移S>M2,符合CASE2条件,所以此时的速度规划中存在匀减速阶段,其加减速仿真曲线如图7所示。

(a) 速度曲线图 (b) 加速度曲线图

由图4～图7的仿真结果可以看出,在行程不足的情况下,加减速算法所规划出的曲线便不是七段的加减速曲线,而是修正后的加减速曲线,根据参数不同,加减速曲线也有相应的变化。在不同的初始参数下,本文所设计的加减速算法均可完成速度规划,仿真曲线连续且光滑。

4 结束语

本文以正弦函数为基础,构建了七段式的Jerk曲线方程,并经过进一步推导,得到改进的加减速控制算法。该算法Jerk曲线变化连续且光滑,减少了加加速度转换点处存在的柔性冲击,简化了计算量。通过仿真结果表明,相较于传统S型加减速,本文算法所构造的速度曲线更加平滑。同时,在不同的初始条件下,均可获得平滑的速度曲线,提高了运动平台的运动精度。