高渗透压脆性岩石循环蠕变宏细观力学机理研究
2023-11-28李晓照贾亚星闫怀蔚戚承志
李晓照,贾亚星,闫怀蔚,戚承志
(1.北京建筑大学 土木与交通工程学院,北京 100044;2.北京未来城市设计高精尖创新中心,北京 100044)
岩石的蠕变力学行为对许多地质灾害(如滑坡和塌方)的预防及人造结构(地下矿山和隧道)的稳定性评价至关重要。在地下工程施工过程中,围岩经常遇到循环加卸载作用,同时受到高渗透压影响而造成破坏。因此,高渗透压静态循环力学特性研究对地下工程中围岩的长期稳定性评价有着重要意义。
许多学者通过渗流-蠕变耦合试验[1-4]或流变模型理论[5-6]分析渗透压力影响下的恒定荷载岩石蠕变特性,发现随渗透压增大,试件的蠕变应变增大。但由于恒定荷载下岩石蠕变时间过于漫长[2],故通过恒定荷载短期试验获取岩石蠕变特性不易实现。因此,学者往往通过应力分级加载研究渗透压作用下岩石蠕变失效特性。Yang[7]和Yi[8]等通过扫描电子显微镜、声发射等技术重点研究了渗透压对应力分级加载下岩石蠕变变形量、蠕变率等力学参数的影响。李晓照[9]和Liu[10]等通过理论和试验方法,研究了渗透压对岩石蠕变裂纹扩展规律的影响,并得出渗透压促进裂纹扩展、增加岩石损伤程度和缩短岩石蠕变失效时间的结论。然而,以上研究均针对应力恒定或分级加载作用下渗透压对岩石蠕变的影响,未能对循环加卸载所造成的岩石循环蠕变破坏进行研究。
Grgic[11]和Xu[12]等利用声发射、电镜扫描等技术分析在循环加卸载蠕变试验中,渗透率和饱和度对岩样蠕变行为的影响,发现砂岩试件在渗透压下循环加卸载相较分级加载破坏强度更低,裂纹体系更复杂。宋勇军等[13]采用分级增量加卸载方式对板岩进行干燥与饱水状态下的蠕变试验,认为水对岩石瞬时变形的影响主要表现在瞬时塑性应变方面;水对岩石黏弹性应变影响显著,对黏塑性应变影响较小。江宗斌等[14]通过循环加卸载条件下的岩石蠕变-渗流耦合试验,分析了岩石加卸载过程中的蠕变、渗透性变化规律,得到压密阶段、裂纹扩展阶段和裂纹贯通阶段岩石体积应变的发展规律,总结了渗透率与体积应变之间的关系。Yan等[15]开展了考虑渗透压时的循环加卸载蠕变试验,以评估其蠕变变形和渗透性能。以上研究无法解释在渗透压作用下,考虑岩石细观裂纹与宏观变形关系的循环加卸载蠕变力学机理。
本文考虑渗透压、围压和循环静态轴向应力加卸载共同作用,基于含初始裂纹与新生翼型裂纹的细观力学模型,对高渗透压下脆性岩石循环蠕变的宏观力学规律展开研究,该理论模型可为深埋富水工程中岩石疲劳寿命的评估和预测提供一定帮助。
1 理论模型
本文提出了一个考虑高渗透压作用的脆性岩石循环蠕变破坏的宏细观力学模型,如图1所示。该模型包含基于高渗透压与外部荷载共同作用下的翼型裂纹扩展模型[9,16]改进的裂纹恢复模型、亚临界裂纹演化法则[17]、Hooke-Kelvin模型[18]、裂纹与应变关系及循环加卸载应力函数。模型采用细观参数平均化方法,假设模型为各向同性体。单个初始裂纹(半径为a)两端分别产生一个翼型裂纹(裂纹长度为l),初始裂纹与轴向应力σ1方向夹角为φ, 令α = cosφ,模型同时还受到围压σ2= σ3作用;脆性岩石的初始损伤定义为D0=NVa3,NV为单位体积内的初始裂纹数量,相邻翼型裂纹贯通长度为a{[3/(4πD0)]1/3-α}[9]。

图1 高渗透压下循环蠕变失效宏细观力学模型原理示意Fig.1 Schematic of the micro-macro model in the cyclic creep failure under high seepage pressure
图1(a)给出了脆性岩石中翼型裂纹相互作用的力学示意图。图1(b)给出了单个完整裂纹的受力原理图。此外,该模型引入轴向应力随时间变化的循环加卸载路径(图1(c)),其在脆性岩石循环蠕变的应变回弹现象中发挥重要作用。
1.1 高渗透压与外部应力共同作用下的裂纹尖端应力强度因子
基于Ashby和Sammis翼型裂纹模型[16]定义的承受远端应力作用下裂纹尖端应力强度因子,将渗透应力PP(图1(b))引入应力强度因子中,则改进的考虑渗透压的Ⅰ型裂纹应力强度因子为[9,19]:
其中,
式(1)~(4)中,β为常数,PP为岩石渗透压应力,FP为渗透应力导致的翼型裂纹开裂的渗透应力,S为含有NV个初始裂纹的单位体积岩石内部单个裂纹面的平均面积, σi3为作用于两个翼型裂纹尖端间的内应力,FW为作用于初始裂纹面上的楔力。理论分析中,压应力取负,反之取正;为了便于观察,在后文图表绘制中压应力取正。
对于FW,以往研究只关注其为张拉力,引起翼型裂纹扩展[9,16,19],根据模型外部应力状态变化,将其分为以下3种情况:
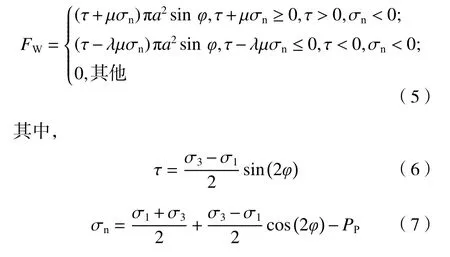
式(5)~(7)中, τ 和 σn分别为内部初始裂纹表面剪应力和法向应力, λ为初始裂纹面反向滑动摩擦折减系数(源于正向滑动导致滑动面粗糙度降低),μ为初始裂纹摩擦系数。
式(5)的第1部分表示初始裂纹面剪切应力克服摩擦产生正向滑动,即楔力大于0,为张拉力,导致应力强度因子为正值,引起翼型裂纹扩展,如图1(a)中Ⅰ区域与图1(b)的正向滑动所示。第2部分表示初始裂纹面剪切应力为反向,并克服摩擦产生反向滑动,楔力小于0,为挤压力,导致应力强度因子为负值,引起已扩展翼型裂纹闭合恢复[20-22],如图1(a)中Ⅱ区域与图1(b)的反向滑动所示。第3部分中其余情况下的剪切力均无法克服摩擦,不产生滑动,定义为0,导致应力强度因子为负值,引起已扩展翼型裂纹恢复闭合。
式(5)中第1部分表达式主要用于第1.2~1.4节中的应力-应变关系研究;式(5)中第1、2、3部分的表达式共同应用于第1.5~1.7节的循环加卸载作用下的循环蠕变特性研究。
1.2 高渗透压作用下裂纹扩展诱发的塑性应力-应变关系
完整岩石变形由弹性、黏弹性、塑性和黏塑性变形组成[23],本文将塑性变形和黏塑性变形统称为塑性变形,并将分别推导考虑渗透压的弹性、黏弹性、塑性阶段的本构方程,进而为循环蠕变研究中应力取值范围及弹性模量的选取提供参考。
理论上,裂纹应力强度因子KI达到临界值KIC时,裂纹扩展。因此,基于式(1)并结合脆性岩石裂纹与应变关系[24],可以推出考虑渗透压作用下,岩石应力状态与裂纹扩展导致的应变关系为:

式(8)~(14)中, ε1为轴向应变,KIC为Ⅰ型裂纹断裂韧度, ε0和m为材料常数, ε1ci为裂纹启裂应变。
1.3 高渗透压作用下弹性与黏弹性应力-应变关系
结合图1(a)与(b)可知,作用于初始裂纹上的剪应力( τ)与其所受摩擦力( µσn)相等之前,裂纹不会产生位移,故两者相等时(此时FW= 0)的轴向应力可作为纯弹性与黏弹性变形阶段的临界应力:
所以,当轴向应力小于 σ1w时,岩石处于纯弹性阶段,将该临界值定义为岩石纯弹性最大应力值,而与之对应的弹性应变可利用裂纹启裂应力(式(8)中翼型裂纹长度为0时的应力值)与纯弹性最大应力比等于裂纹启裂应变与纯弹性应变比的关系(即σ1ci/σ1w=ε1ci/ε1e)近似求解:

式中,EW为弹性模量。
对于纯黏弹性变形阶段( ε1e<ε1<ε1vepmax,ε1vepmax为施加轴向最大黏弹性应力 σ1vepmax时的轴向应变,ε1ci<ε1vepmax),可将弹性模量随轴向应变演化关系定义为:
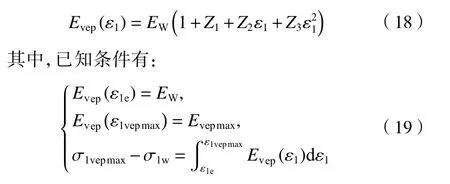
式中,Evepmax为纯黏弹性阶段发生最大应变时的弹性模量,可根据式(8)绘制的应力-应变曲线的斜率确定。
将式(18)与(19)联立可得到系数Z1、Z2、Z3,进而得出黏弹性阶段的应力-应变本构关系为:
1.4 高渗透压下完整弹-黏-塑性应力-应变关系
由式(8)、(17)和(20)得到高渗透作用下弹性、黏弹性和塑性变形阶段的应力-应变本构方程为:
值得注意的是,以上初始裂纹正向滑动翼型裂纹扩展诱发的应力-应变关系为循环静态加卸载作用下,循环蠕变方程中应力状态 (σ1,σ3)及弹性模量EW参数的选取提供了基础数据。
1.5 渗透压作用下弹性与黏弹性循环蠕变方程
Hooke-Kelvin模型由胡克弹簧和开尔文体串联而成,可以很好地描述岩石黏弹性阶段的变形情况,其表达式为[18]:
式中,EW为脆性岩石弹性模量,Evet为黏弹性模量,η为黏度系数, σ˙1、 ε˙1分别为应力率和应变率。
将已知条件 |σ˙|=0 和 ε1(t=0)=|σ1L|/EW代 入 式(22),可以得到恒定荷载条件下轴向黏弹性应变随时间变化的方程为:
式中, σ1L为轴向应力第1次循环静加载值。

式中: σ1L(t) 和 σ1UL(t)分别为循环加卸载应力状态(图1(c))中的除第1次静加载外的加载轴向应力与全部卸载轴向应力;tveL为式(23)中黏弹性应变的加载时间,需要说明的是,此后每个循环加卸载轴向应力的作用时间t都是相互独立的。
经过第1次循环加卸载,可以得到下一次静加载时的初始应变条件为:
同理,可以得到下一个循环加卸载应力状态中静态加载下随时间变化的黏弹性应变的表达式:
式(25)、(26)中, σ1LN为下一次静力加载值,tveUL为黏弹性应变的卸载时间。
1.6 高渗透压作用下翼型裂纹扩展、恢复诱发的塑性循环蠕变方程
在恒载条件下,裂纹扩展引起的瞬态、稳态和加速状态的纯塑性蠕变阶段轴向应变可用翼型裂纹变化引起的轴向应变[24]与裂纹启裂应变的差表示:
式中,l(t)为翼型裂纹长度随时间演化值,可将式(1)应力强度因子代入亚临界裂纹演化法则dl/dt=v(KI/KIC)n[17],即求解以下微分方程获取:
式中,v为特征裂纹速度,n为应力侵蚀指数。上述微分方程初始裂纹长度值可通过求解方程(21)在特定应力状态下的裂纹长度确定。将循环加卸载应力路径代入微分方程(28),可以求解裂纹扩展与裂纹恢复导致的翼型裂纹长度演化结果。本文假设裂纹恢复时间演化法则也服从式(28)的亚临界裂纹变化法则[17]。裂纹恢复现象机理为[22]:1)初始裂纹面正向滑动产生翼型裂纹扩展以后,由于围压保持恒定,轴向应力卸载至一定临界值时,导致初始裂纹面产生反向滑动,已扩展翼型裂纹产生的恢复现象;2)当初始裂纹面无法克服摩擦滑动时,在围压作用下,由于不同翼型裂纹尖端间岩石颗粒的压融机理,导致已扩展翼型裂纹闭合恢复。
1.7 高渗透压作用下完整弹-黏-塑性循环蠕变方程
结合式(23)、(24)、(26)和(27),得到应力循环加卸载下考虑弹性、黏弹性和塑性应变随时间变化的循环蠕变方程为:
2 理论模型的计算结果与讨论
基于上述理论模型,对高渗透压作用下脆性岩石应力-应变关系及循环蠕变演化结果进行研究。具体模型参数选取方法参考文献[9,19]。
2.1 高渗透压下岩石弹-黏-塑性应力-应变关系
脆性岩石在准静态荷载下得到的应力-应变本构关系可以为循环蠕变过程中轴向应力初始应力值、卸载值、加卸载幅值、弹性模量等应力参数的选取提供依据,故有必要对其进行讨论。
本文考虑高渗透压的本构模型参考了文献[19]提出的高渗透压作用下脆性岩石宏细观力学本构模型,并增加了纯弹性及纯黏弹性阶段应力-应变状态分析。图2给出了砂岩不同渗透压作用下考虑弹-黏-塑性应力-应变本构曲线理论结果与试验结果[25]的对比,其模型参数为KIC=0.69 MPa·m1/2,D0=0.059,m=2,φ=36°, ε0=1/78, µ =0.49,a=1.77 mm, β=0.29,纯黏弹性最大轴向应力 σ1vepmax选取0.8 σ1peak[26]。
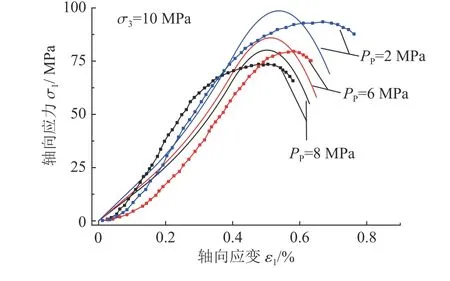
图2 不同渗透压下应力-应变关系理论与试验结果[25]对比Fig.2 Comparison of theoretical and experimental data[25]in stress-strain curves under different seepage pressure
由图2可知:理论与试验曲线变化趋势相同,数值上具有可比性,验证了模型合理性。同时,理论与试验曲线也存在一定差异,原因可能是:1) 本文模型中所有裂纹角度、尺寸均假设为相同,是一种平均化的方法;2) 本文模型仅研究水的渗透压力作用,忽略了水岩化学作用因素的影响;3) 模型参数选取存在一定误差。
弹性模量是岩石的重要力学参数,在考虑渗透压下的Hooke-Kelvin模型研究中发挥着较为重要的作用。图3为不同围压影响下,弹性模量EW随渗透压的变化趋势。由图3可知:随着围压的增大,相同渗透压下的弹性模量也随之增大;相同围压作用下,弹性模量随渗透压的增加而减小。

图3 渗透压与弹性模量关系Fig.3 Relation of seepage pressure to elastic modulus
2.2 高渗透压对脆性岩石循环蠕变失效特性的影响
基于式(29),图4给出了考虑高渗透压的砂岩和玄武岩应变随时间的演化曲线。图4中:砂岩的模型参数为KIC=0.69 MPa·m1/2,n=16,D0=0.059,m=2,ε0=1/98, µ =0.433,λ=0.5,a=2.4 mm,φ=36°,v=1.7 ×10-9m/s, β=0.29,Evet=90 GPa, η=106GPa·s;玄武岩的模型参数为KIC=1.48 MPa·m1/2,n=57,D0=0.048,m=2,φ=38°, ε0=1/78, µ=0.48,λ=0.5,a=3.1 mm,v=1.7 ×10-9m/s, β=0.29,Evet=130 GPa, η=106GPa·s。由图4可以看出,理论结果与试验结果[12,15]变化趋势一致,具有一定的可比性,验证了模型的合理性。两者差异主要是由模型各种假设条件及参数选取误差所致。上述两种岩石的理论结果中均未出现裂纹恢复引起的塑性回弹现象,主要是由于试验中应力未达到塑性回弹的应力条件,总应变中的回弹现象主要是黏弹性回弹引起的。
高渗透压作用下的弹-黏-塑性循环蠕变的相关变量随时间的演化如图5所示。图5中,部分参数与图2中应力-应变本构关系保持一致,其余参数为n=51,v=1.1 ×10-7m/s,λ=0.3,Evet=50 GPa, η=6×106GPa·s。

图5 高渗透压影响下各变量与时间关系曲线Fig.5 Curves of time-dependent variables under different seepage pressures
图5(a)为图1(c)中轴向循环加卸载应力函数的具体描述。在此应力状态下,由图5(b)可知:轴向应力加载阶段,楔力为正数,导致初始裂纹面正向滑动;轴向应力卸载阶段,楔力始终为负数或0,导致初始裂纹面的反向滑动。由图5(c)可知,在渗透压9 MPa作用下,应力强度因子在加载阶段为正,在卸载阶段为负。非正楔力和负强度因子导致已扩展翼型裂纹恢复(图5(d) ),引起图5(e)中纯塑性轴向应变回弹。
图5(d)与(e)中:随着循环次数增加,加载阶段的翼型裂纹长度最大值与轴向应变最大值不断增大;卸载阶段的裂纹长度与轴向应变最小值先增大,后保持不变。以上导致了纯塑性回弹应变先减小后增大的变化趋势,如图6所示。

图6 纯塑性应变ε1p回弹值计算结果Fig.6 Computational results of rebound value of plastic strain ε1p
由图6可知:随渗透压增大,给定加载阶段的翼型裂纹长度与轴向应变不断增大,卸载阶段的翼型裂纹长度与轴向应变也增大;以上导致了第7次卸载阶段的纯塑性回弹应变增大,如图7所示。

图7 高渗透压对黏弹性应变与纯塑性应变回弹值的影响Fig.7 Effects of seepage pressure on the rebound values of viscoelastic and plastic strain
图5(f) 中:同一渗透压下,每次循环加载阶段,黏弹性轴向应变 ε1ve随时间的增加而减速增大;在卸载阶段,随时间的增加而减速减小。每次循环加载时的黏弹性应变最大值(称为加载应变)和卸载时的最小值(称为卸载应变)均随渗透压增大而增大,但渗透压对加载应变的影响效果明显大于卸载应变(图5(g))。进一步分析可知,渗透压增大导致了黏弹性回弹应变的增大(图7是图5中第7次卸载的回弹值)。
图5(h) 中,循环蠕变轴向总应变是结合黏弹性应变和塑性应变得到的。无论在加载还是卸载阶段,轴向总应变都随循环次数的增加而增大;累积轴向应变逐渐增大,直至最终破坏应变。结合渗透压与循环蠕变失效时间tf关系曲线(图8)可以发现,随着渗透压的增加,循环蠕变失效时间逐渐缩短,且两者近似呈线性关系。

图8 渗透压与循环蠕变失效时间tf关系曲线Fig.8 Effect of seepage pressure on time to failure under cyclic creep
表1给出了不同渗透压下循环蠕变失效应力及本构关系中得到的峰值应力。由表1可知,随着渗透压的增加,循环蠕变失效应力有所减小,但与之对应的峰值应力也随之减小。对比发现,渗透压几乎不会引起循环蠕变失效应力与峰值应力的比例发生改变。

表1 渗透压下循环蠕变失效应力与峰值应力关系Tab.1 Relationship between peak stress and cyclic creep failure stress under seepage pressure
2.3 围压对高渗透压下脆性岩石循环蠕变失效影响
围压对高渗透压下脆性岩石蠕变特性有着重要的影响。然而,由于试验时间、试验条件等因素的限制,长时间高围压、高渗透压等应力状态往往难以通过常规蠕变试验实现。因此,基于本文的高渗透压下脆性岩石循环蠕变宏细观模型,通过理论方法探究围压的影响。
图9为在与图5(a)保持相同的轴向应力循环加卸载作用下,在渗透压为10.0 MPa时围压对脆性岩石循环蠕变的影响曲线。
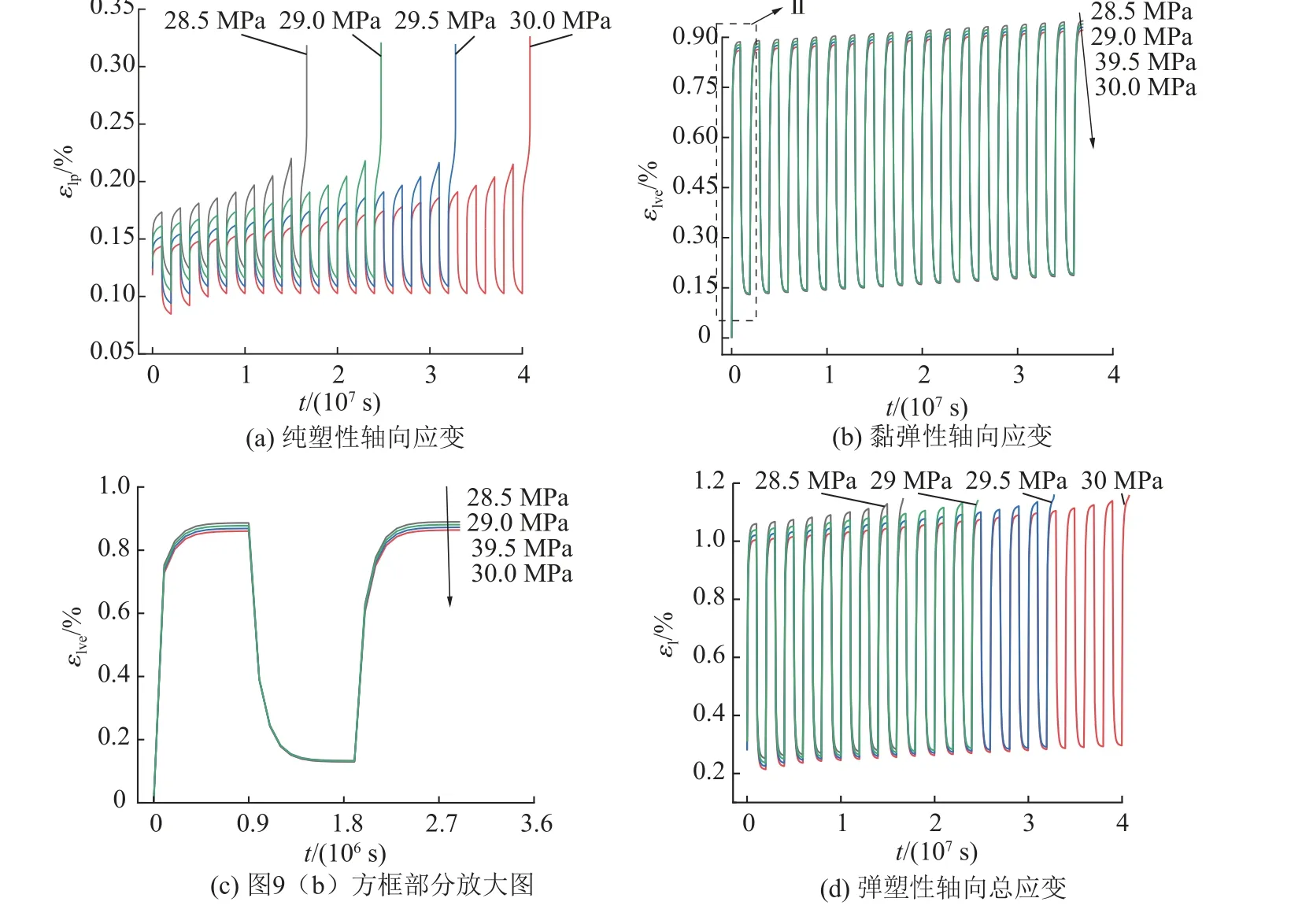
图9 围压影响下各应变与时间关系曲线Fig.9 Curves of strain and time under different confining pressure
由图9(a) 可知,相同轴向应力下,围压越大,纯塑性应变越小。由图9 (b)和(c)可知,随着围压的增大,黏弹性轴向加载和卸载应变均有所减小。由图9(d) 可知,围压越大,总应变值越小,循环蠕变失效时间越长。图10总结了第5次卸载阶段的回弹值。由图10可知,随着围压增大,黏弹性与纯塑性应变回弹均减小,说明围压抑制蠕变应变回弹,减缓了循环蠕变失效。
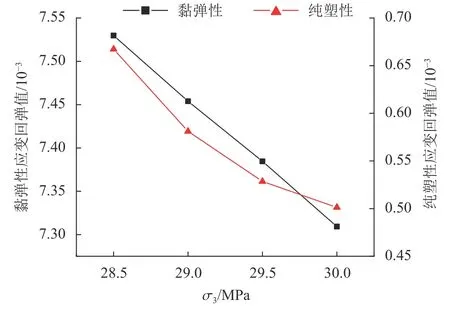
图10 围压对黏弹性应变与纯塑性应变回弹值的影响Fig.10 Effects of confining pressure on the rebound values of the viscoelastic and the pure plastic strains
3 结 论
基于考虑裂纹恢复机理的高渗透压翼型裂纹改进模型、亚临界裂纹演化法则、裂纹与应变关系及Hooke-Kelvin模型,建立了一种高渗透压影响下考虑弹-黏-塑性的脆性岩石循环蠕变宏细观力学模型。具体结论如下:
1)当围压恒定时,弹性模量EW随着渗透压力的增大而不断线性减小;相同渗透压下,围压越大,弹性模量越大。
2)在轴向应力循环加卸载与恒定围压下,渗透压越大,岩石黏弹性应变、塑性应变、总应变及回弹值均随之增大,而循环蠕变失效应力越小且失效时间越短。即渗透压促进了应变回弹,加速了循环蠕变失效,但渗透压并不会引起循环蠕变失效应力与峰值应力的比例发生改变。
3)在轴向应力循环加卸载与恒定渗透压下,围压越大,岩石黏弹性应变、塑性应变、总应变及应变回弹均减小,循环蠕变失效时间延长,即围压抑制了应变回弹,减缓了循环蠕变失效。
