红松人工林叶面积分布规律及回归模型研究
2023-11-28李鑫贾炜玮
李鑫 贾炜玮
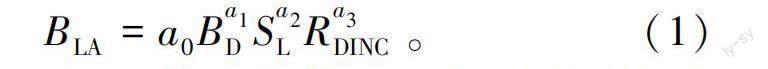
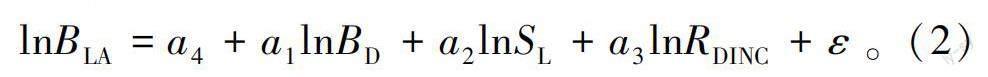
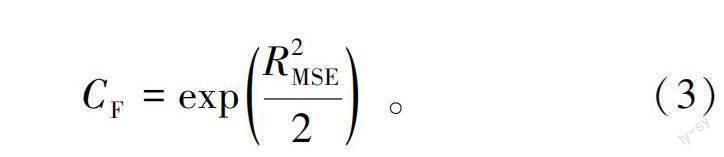
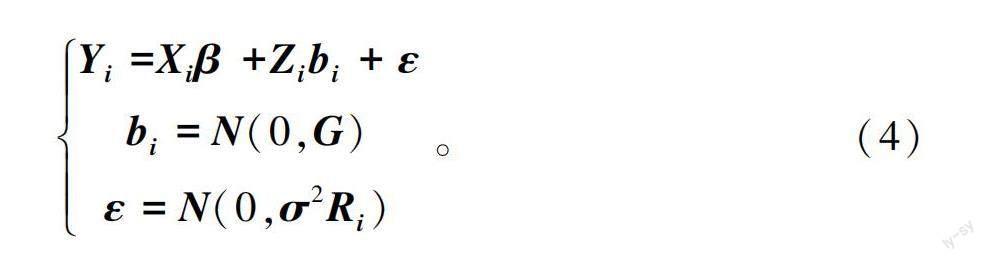
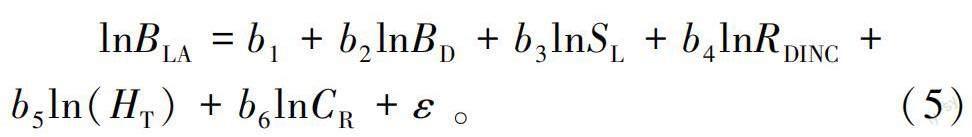


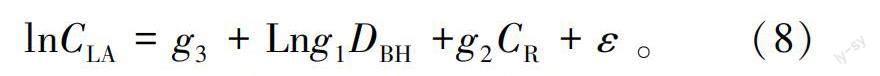

摘 要:葉面积的大小可以对树木的生长和生命活动产生深远的影响,进而关系到树木生物量的变化和森林生态的发展趋势,叶面积的研究可以对树木的相关分析起到较为关键的作用。基于黑龙江省48株红松人工林解析木数据和排水法测定的叶面积数据,建立基础线性回归模型,后引入随机效应参数构建混合效应回归模型以提高拟合效果和预估精度。在加入树木层次的随机效应时,最终得到的最优混合效应模型含有3个随机效应参数,分别为枝条基径的对数(lnBD)、枝条长度的对数(lnSL)、树高的对数(lnHT)。该模型的R=0.86,平均绝对偏差M=0.342 8,均方根误差R=0.484 1,统计指标较仅包含固定效应的基础线性模型均有较好的提高。综合分析得出该模型可以较好地对红松枝条叶面积大小进行描述。基于该模型计算红松树冠叶面积并得到混合效应预估模型,混合模型的R=0.83,R=0.442 9。通过检验结果可知该模型可以较好地对红松树冠叶面积进行预估计算,为日后该地区人工红松的经营提供良好的指导方向。
关键词:红松;枝条叶面积;回归模型;混合效应;排水法
中图分类号:S 文献标识码:A 文章编号:1006-8023(2023)06-0001-11
Study on the Distribution Law and Regression Model of Leaf
Area in Korean Pine Plantation
LI Xin, JIA Weiwei
(School of Forestry, Northeast Forestry University, Key Laboratory of Sustainable Management of Forest Ecosystem, Ministry of Education, Harbin 150040, China)
Abstract:The size of the leaf area can have a profound impact on the growth and life activities of the tree, and then it is related to the change of the biomass of the tree and the development trend of the forest ecology. The research on leaf area can play a key role in the correlation analysis of trees. Based on the analytical wood data of 48 Korean pine plantations in Heilongjiang Province and the leaf area data measured by the drainage method, a basic linear regression model was established, and then random effect parameters were introduced to construct a mixed effect regression model to improve the fitting effect and prediction accuracy. When random effects at the tree level were added, the optimal mixed effect model obtained contained three random effect parameters, namely logarithm of branch base diameter(lnBD), logarithm of branch length (lnSL), and tree height logarithm(lnHT). The Rwas 0.86, the MAE was 0.342 8, and the RMSE was 0.484 1. The statistical indicators were better than the basic linear model that only included fixed effects. The comprehensive analysis showed that the model can better describe the leaf area of Korean pine branches. Then, based on the model, the crown leaf area of the Korean pine tree was calculated and a mixed effect prediction model was obtained. The mixed model R was 0.83 and the RMSE was 0.442 9. Through the test results, it can be seen that the model can predict the crown and leaf area of Korean pine trees better, and provide a better guiding direction for the future management of artificial Korean pine in this area.
Keywords:Korean pine; branch leaf area; regression model; mixed effect; drainage method
收稿日期:2023-02-15
基金项目:国家自然科学基金区域创新发展联合基金重点项目(U21A20244);中央高校基本科研业务费专项资金项目(2572019CP08;2572022DT03)。
第一作者简介:李鑫,硕士研究生。研究方向为树木生长模型、森林经理等。 E-mail: 654822408@qq.com
*通信作者:贾炜玮,博士,教授,博士生导师。研究方向为树木生长收获模型、森林经理等。 E-mail: jiaww2002@163.com
引文格式:李鑫,賈炜玮. 红松人工林叶面积分布规律及回归模型研究[J].森林工程,2023,39(6):1-11.
LI X, JIA W W. Study on the distribution law and regression model of leaf area in Korean pine plantation[J]. Forest Engineering, 2023, 39(6):1-11.
0 引言
光合作用对于植物的生命活动具有非常重要的作用,而树叶作为树木不可或缺的一部分,其作用是树木进行光合作用和蒸腾作用的主要器官和平台。树木进行光合作用的效率由树叶决定,而树叶的面积大小则是其中至关重要的因素,所以叶面积的大小将对树木的生长和树木生物量的累积产生较为深远的影响。在现代林业研究中,叶面积也同时作为森林群落结构和森林生产力的主要评价指标之一,树木叶面积的研究也是构建森林生态系统生产力模型的重要任务,在对森林生态系统全球变化趋势的预测中充当着重要的一环,针对叶面积以及叶面积预测模型的研究在全球范围内引起了高度重视,所以如何准确获取树木叶面积并提高精度成为了当前林业研究的一个重要内容。
与较为平整且舒展的阔叶相比,红松一类针叶树种的叶面积就难以直接测量。一方面对叶面积的测量需要对树木进行解析木工作,对树木造成不可逆的破坏,因为试验需要大量样本数据,因此成本和代价极高;另一方面,针叶树种的树叶呈现多针多束的特点,测量叶面积将会耗费大量人力和时间,其测量误差因人而异也不可避免。因此构建一个精度较高拟合效果较好的叶面积预估模型显得尤为重要,模型可以灵活且广泛应用于各个树种树木的叶面积研究工作中。根据树木的生长特性和以往学者的研究可知,如今绝大部分的叶面积研究都在重点研究预估模型的建立。根据管道模型理论可知,叶面积的大小和树木自身胸径、树木高度、枝条长度、枝条基径和着枝深度等容易获得的解析木属性因子有关。而构建叶面积模型的基础模型的选取和提高精度的方法就显得尤为关键。研究表明,在所有解析木属性因子中,枝条基径、枝条长度和相对着枝深度可以相互结合对枝条叶面积进行较好的预测,引入树木层次,例如胸径、树高和冠长率等因子可以提高叶面积模型的预估效果。
本研究数据来源于黑龙江省林口林业局内48株人工红松解析木数据,使用排水法进行叶面积的测定,使用包括枝条长度、枝条基径在内的相关属性因子作为自变量构建红松枝条层次叶面积的基础模型,为了提高模型的拟合效果和精度,再引入包括胸径、树高、冠长在内的树木层次的因子作为随机变量进行混合效应模型的构建。
红松作为主要珍贵经济树木,其价值在各个方面都有所体现,然而对于红松的叶面积研究和空间分布规律研究却较为稀少。为此,本研究以黑龙江省林口林业局内48株人工红松解析木数据为基础,使用排水法[6]进行叶面积的测定,使用包括枝条长度、枝条基径在内的相关属性因子作为自变量构建红松枝条层次叶面积的基础模型,为了提高模型的拟合效果和精度,再引入包括胸径、树高、冠长在内的树木层次的因子作为随机变量进行混合效应模型的构建,为我国东北林区红松生长经营提供帮助。
1 研究区域概况与数据收集整理
1.1 研究区概况
红松相关数据来自黑龙江省牡丹江市林口县林口林业局(129°40′~130°34′ E,45°51′~45°59′ N)内的样地,样地所在区域地貌为低山丘陵地形,海拔400~800 m,年均降水量560 mm,年均温度为2.4 ℃,林区是典型的寒温带大陆性季风气候,暗棕壤、白浆土和草甸土等为其主要的土壤类型。样地所在区域树种较多,主要乔木为包括红松(Pinus koraiensis)、云杉(Picea asperata)、冷杉(Abies nephrolepis)、兴安落叶松(Larix gmelinii)、樟子松(Pinus sylvestris var. mongolica)、水曲柳(Fraxinus mandshurica)和柞树(Quercus mongolica)等。
1.2 数据的采集和整理
1.2.1 标准地相关信息
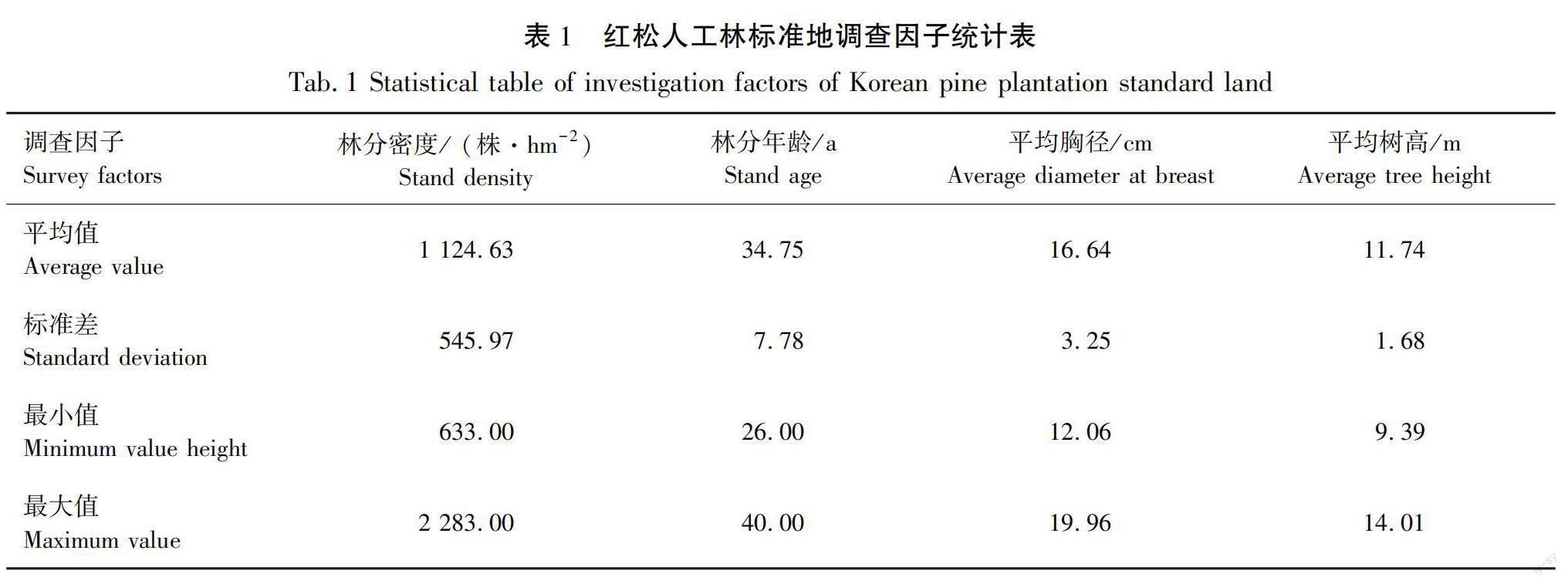
本研究数据来自于黑龙江省牡丹江市林口县林口林业局内红松人工林样地,在该区域内于2019年6月设置了16块大小均为30 m×20 m的红松人工林标准地,在对经纬度、海拔和坡度等因子进行记录后,进行每木检尺。即通过测定标准地内每一株树木的胸径树高等因子,求得相关林分调查数据。结果见表1。
1.2.2 解析木的测定及处理
在完成每木检尺相关工作后,根据等断面积径级标准木法,结合树木长势,在每块标准地边界外侧附近选取了5株人工红松进行树木解析,另外基于每木检尺数据选取出1株优势木和1株劣势木。优势木的选取标准是贴合每木检尺中胸径较大的前6株胸径的平均值,同样劣势木的选取则是贴合每木检尺中胸径较小的前6株胸径的平均值。然后在每块标准地内选取出在胸径、树高等方面都能代表标准地内树木平均水平的红松作为平均木。本次共获取到48株红松,后进行解析木数据获取。
在对以上48株红松进行树木解析后,得到了包括树木胸径(Diameter at Breast Height,DBH)、树高(Height of Tree,HT)和冠幅(Crown Width,CW)等在内的基本数据项,然后根据北方向对树木进行伐倒。根据红松的生长规律可知,相同年龄的一级枝条会分布在红松树干的一定区域范围内,每一个不同的区域称作一轮,即可简单认为每一轮内的枝条均为同一年龄。对每一轮内的枝条按照方向顺序进行编号,然后对每一根一级枝条进行数据测量,数据包括枝条生长的着枝角度、着枝深度、总着枝深度、方位角、枝条长度(Shoot Length,SL)和枝条基径(Base Diameter,BD)等,使用枝剪对枝条进行分解,测量枝条的重量。再通过选取每一轮中长势较为良好且可以代表其他枝條生长水平的枝条作为标准枝条进一步的数据测量,即对该枝条进行枝叶分离,分别测量不带叶枝条和针叶的重量。由于枝条数量过多且无法完整带回进行内业处理,故对以上所有符合标准的枝条和针叶分别取样并称重记录。后将样品带回进行内业处理,包括排水法测量样品叶面积和烘干操作获得样品干重用以计算生物量等。
1.3 排水法测定叶面积
根据以往关于叶面积测定方法的研究,常见的方法有叶面积仪测定法、剪纸测定面积法、方格纸测定法、扫描测定法和通过拍摄图像进行计算等,在通过分析红松针叶特性后,本研究拟选取排水法作为叶面积测定的主要方法。因为对比其他叶面积测定方法,排水法在测定时无须对针叶的宽度和厚度进行全部测量,这种较为方便直接的方法在测量数量较多的样本时具有良好优势。
使用排水法测定红松叶面积的基本步骤为:将盛有水的容器放在精度较高的电子秤上(设水的密度为标准密度,即1 g/cm),样品根据长度不同进行分组,每组样品的针叶浸没于容器里,待气泡消失后读取操作前后电子秤的数值,其差值即为所测量的叶片体积。通过体积和之前的长度可以计算出该样品分组的红松叶片叶面积。可以根据所求出的样品叶面积与其鲜重进行计算,求出单位重量的叶面积,再通过外业数据中的标准枝条枝叶鲜重换算出整个枝条的叶面积。
1.4 数据的采集和整理
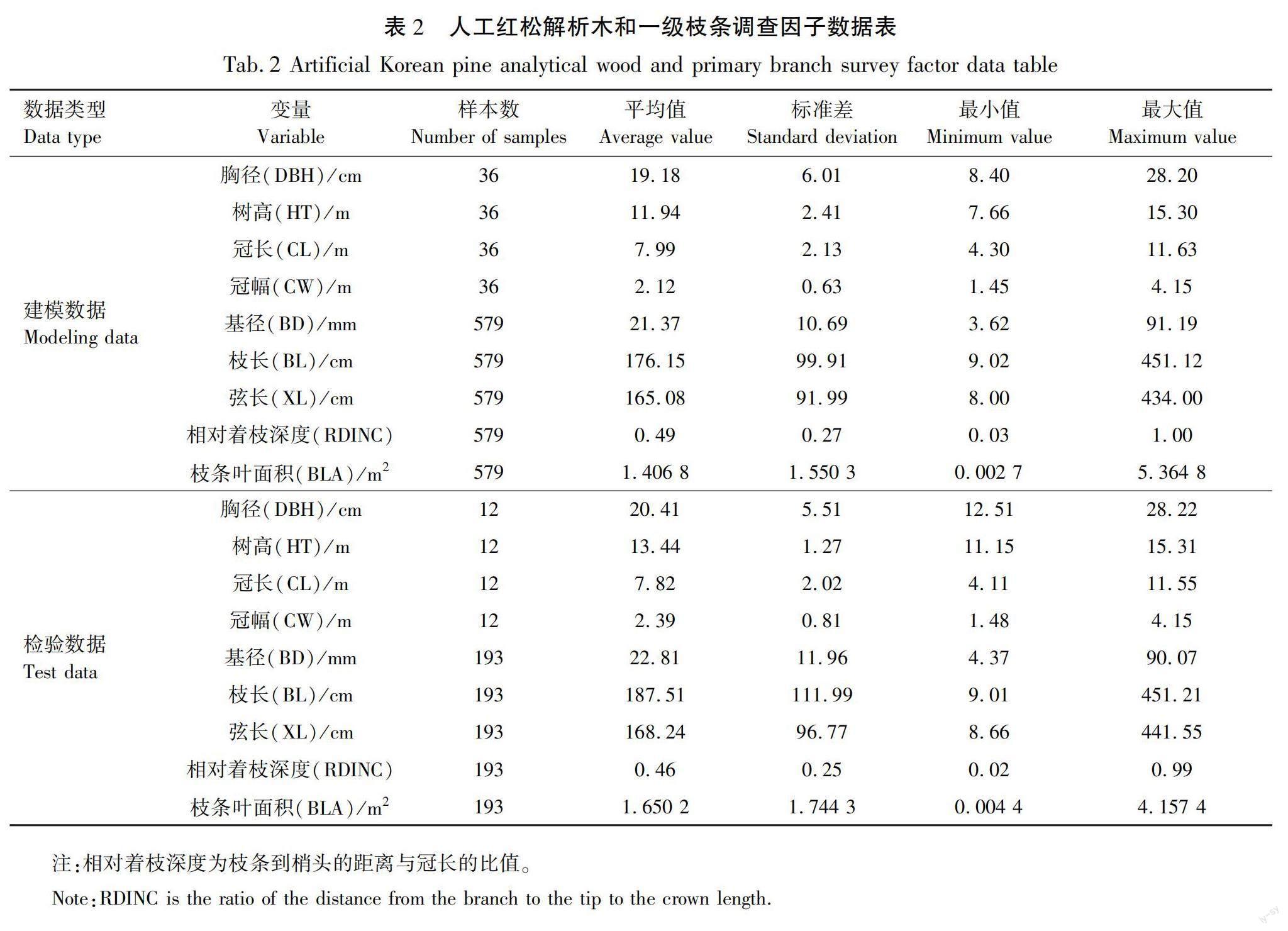
由解析木测定得到的48株人工红松基础数据和由排水法测定得到的772根一级枝条叶面积数据整理见表2。
在这48株人工红松解析木一级标准枝条数据中随机选取75%进行模型构建工作,剩余的25%数据用来模型的独立检验,用以评价模型的拟合效果和精度。模型的相关处理和计算采用统计软件R 4.0.5完成。
2 研究方法
2.1 红松一级枝条叶面积(BLA)基础模型的建立
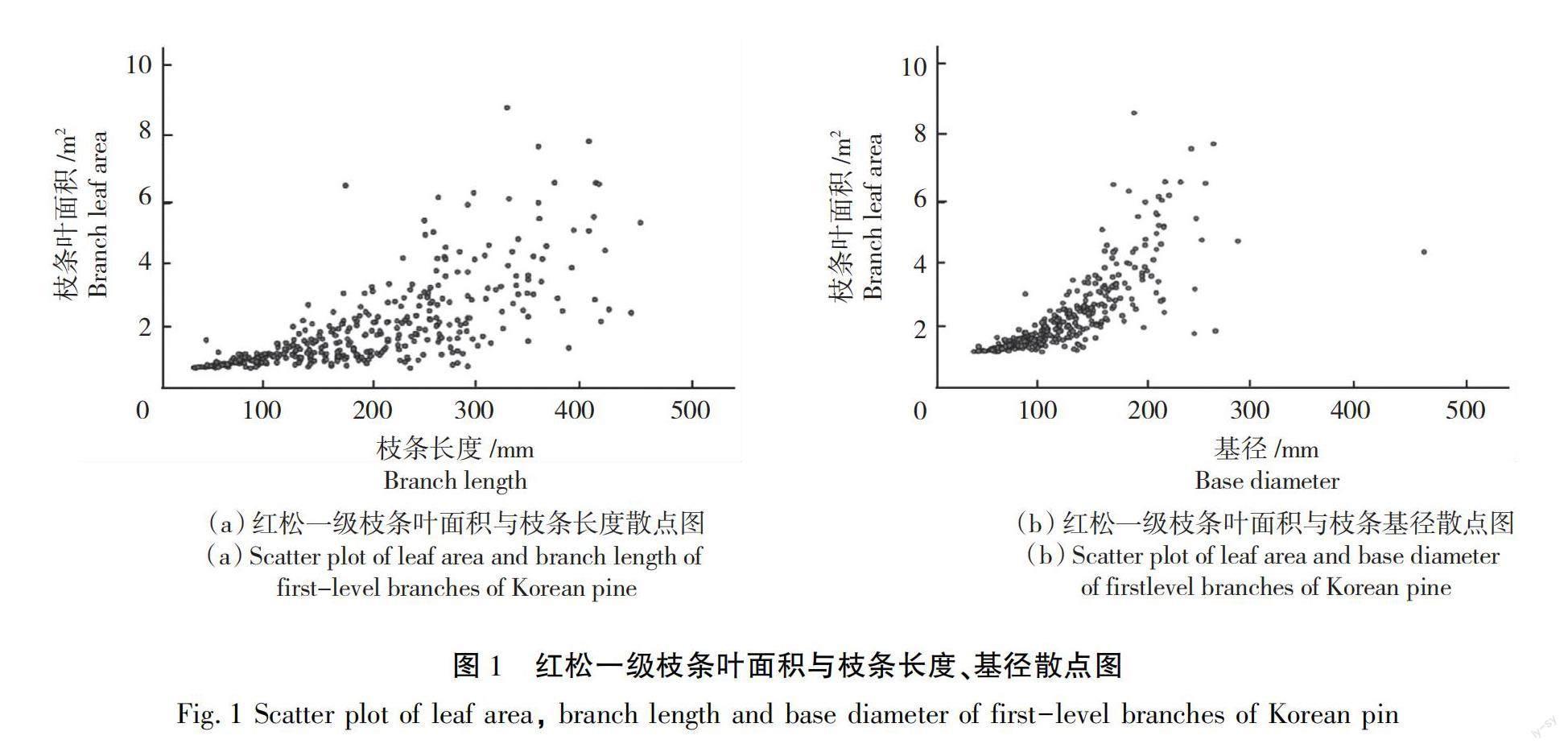
根据以往关于树木一级枝条叶面积的研究表明,树木的枝条叶面积与枝条长度、枝条基径和枝条相对着枝深度都具有一定的相关关系,即在对相对着枝深度进行分组后可以发现,在每一组中枝条叶面积的差异较大,而在不同分组中枝条叶面积的变化趋势为先增大后减小。图1为使用建模数据中红松枝条的枝条长度、枝条基径和枝条叶面积建立的散点图,通过分析图形关系可知红松枝条叶面积与其枝条长度、基径呈现非线性相关关系。
结合图1的作图规律,本次对于红松人工林枝条叶面积的模型构建的研究选择红松枝条长度、基径以及枝条相对着枝深度作为自变量,初步的基础模型形式如下。
式中:a、a、a、a为模型参数;B为红松枝条叶面积,m;B为红松枝条基径,mm;S为红松枝条长度,cm;R为相对着枝深度。
非线性方程的拟合效果受参数的初始值影响,且不易收敛,对后期的模型优化具有较大影响,因此将式(1)作对数转换得到如下形式。
式中:a=lna;ε为误差项,其他参数意义同上。
因为在对数转换时会产生偏差,为了减小该偏差所带来的影响,可以引入校正系数CF(式中用C表示)。
式中,R为式(2)的均方根误差。
由于基础模型的自变量过少导致拟合效果不能达到最好,所以本研究将解析木数据中树木层次的部分属性因子作为自变量引入基础模型。使用统计软件SPSS中参数步进的方法,在式(2)中加入胸径(DBH)、高径比(HT/DBH)、冠幅(CW)和冠长率(CR)等属性因子,对不同自变量组合情况下的模型进行拟合,通过模型显著性对比,将具有更好显著性的自变量组合引入模型得到进一步的基础模型形式。
2.2 基于基础模型的混合效应模型的构建
由于基础线性模型只有固定效应,在枝条叶面积的研究中不仅要考虑到各个枝条,还需要考虑到这些枝条来自不同树木,即树木层次的随机效应也需要引入到模型当中。最后通过分别引入枝条层次的固定效应和树木层次的随机效应进行混合效应模型的构建。通过查阅相关资料和阅读以往研究可知,带有随机效应的混合线性模型相较于基础线性模型往往具有更好的拟合效果和预测精度。
混合效应的一般模型形式为
式中:Y是第i个类别中的n×1次观测值;X是n×p维固定效应设计矩阵;β是p×1维固定效应参数向量;Z是n×q维随机效应设计矩阵;b是q×1维随机效应参数向量,且b期望为0,方差为G;G为q×q维矩阵,协方差计算公式Cov(b,b)=0,i≠j表示b间彼此独立;ε为n×1维误差向量,期望为0,方差为σR; σR为n×n维矩阵;ε和b的协方差为0。
2.3 红松树冠叶面积(CLA)基础模型的构建
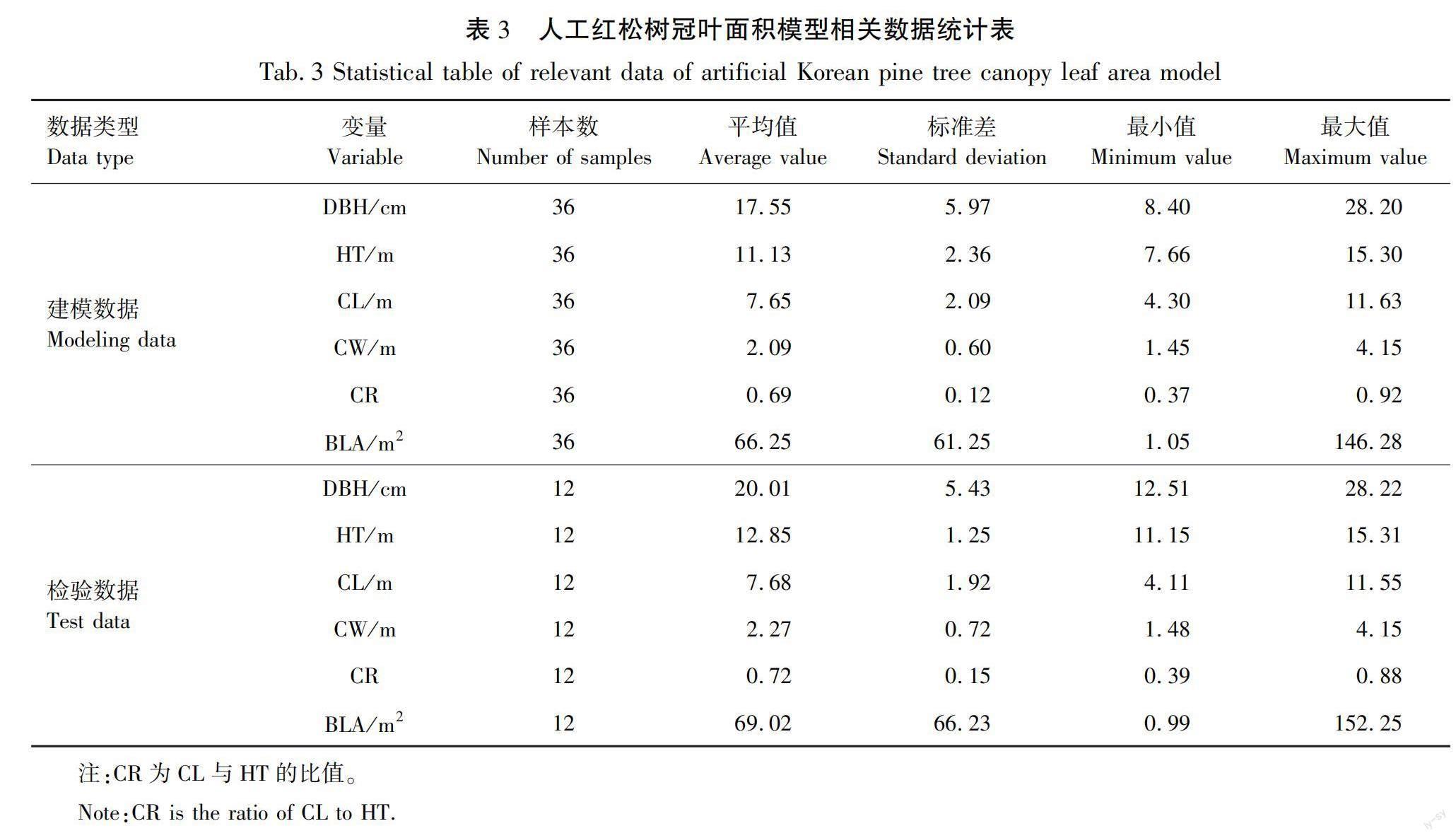
本研究对于红松树冠叶面积的计算方法采用的是基于Maguire等、苗铮等研究的“枝条求和法”。即使用本研究前面所建立的红松枝条叶面积模型对整株红松的所有枝条叶面积进行计算求和,最后所得的结果就是单株红松的树冠叶面积。然后将所得数据按照3∶1的比例进行分组,作为建模数据组和检验数据组,相关数据见表3。
同之前的研究一致,还是考虑引入所有相关的自变量因子,即包括胸径、树高、冠幅和冠长率等。将以上自变量分别与通过“枝条求和法”求得的红松树冠叶面积进行相关性分析后寻找出大致规律,再通过对Maguire等研究中所提出的树冠叶面积模型的带入,综合各种自变量组合方式带入后的模型拟合效果选择最好的一组作为红松树冠叶面积的基础模型。使用上文中构建红松枝条叶面积预估模型的思路和方法,即通过引入随机效应,建立出具有随机效应的红松树冠叶面积预估模型,使得模型拥有更好的拟合效果和更高的拟合优度。
2.4 叶面积回归模型的评价和检验
在参考以往对于混合效应模型评价和研究所使用的指标后,决定选取以下评价指标对模型的拟合进行评价与检验,见表4。
3 结果与分析
3.1 枝条叶面积混合模型的建立
通过参数步进的方法,将树木层次的属性因子分别引入式(1)。结果发现,参数a与树高、冠长率具有相关关系,将上述2个树木层次的属性因子代入式(2)并作对数转换后得到最后的基础线性模型如下。
式中:b—b为模型待估计参数;H为树高;C为冠长率。
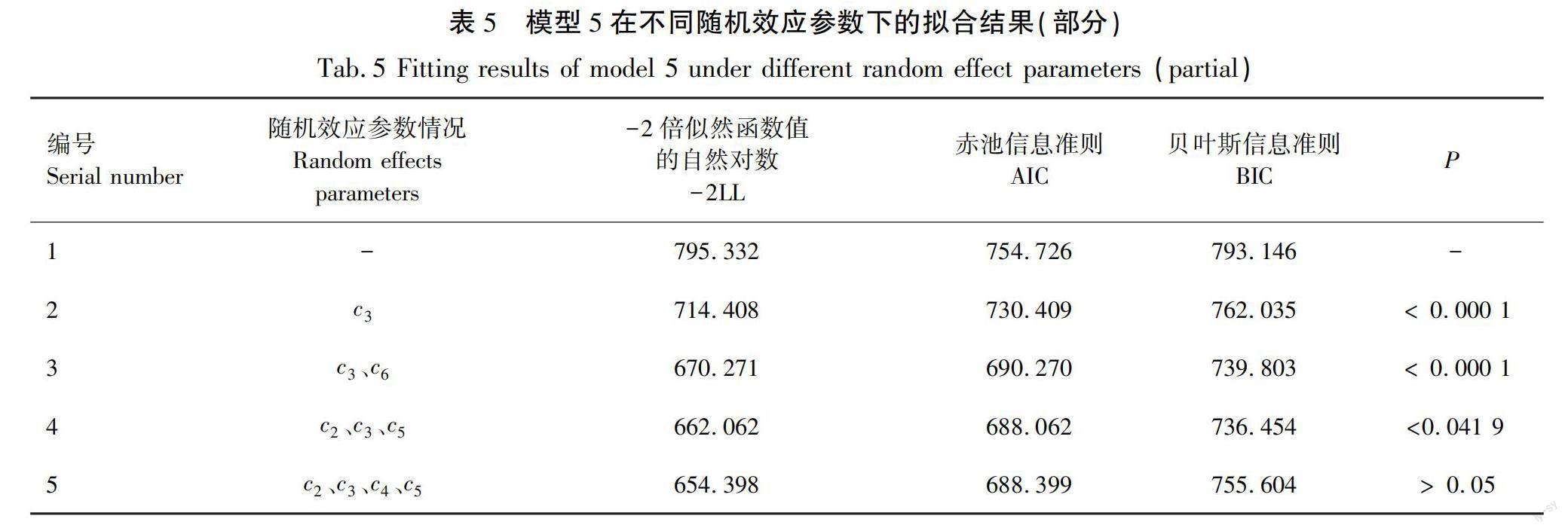
向式(5)中加入树木层次的随机效应以构建混合效应模型。随机效应参数个数有6种组合,引入的随机效应位置有6种可能,经过排列组合计算,混合效应模型共有63种不同的组合形式。经过计算发现,当引入的随机效应参数个数超过3个时,模型变为不收敛。表5对引入随机效应参数个数为0、1、2、3个时拟合效果最好的混合模型评价指标分别进行展示。
由表5可知,1号模型和2号模型具有极显著差异(P<0.001),2号模型和3号模型也具有极显著差异(P<0.001),3号模型与4号模型对比同样具有显著差异(P<0.05),4号模型与5号模型的差异则显示为不显著(P>0.05)。再经过对比AIC、BIC与-2LL这3个评价指标的数值,得出模型拟合效果最好的为4号模型,其模型具体表现形式为
lnB=b+(b+c)lnB+(b+clnS+blnR+(b+c)ln H+blnC+ε。 (6)
式中,c—c为混合模型随机效应参数。
其中,在引入随机效应时,需要在统计软件中选择模型计算所使用的协方差类型,根据以往相关数据研究和查阅相关资料,本研究使用了包括对角化、复合对称和非结构化在内的3种协方差类型分别进行拟合计算,通过对比模型拟合的评价指标后,非结构化协方差类型下的模型拟合效果最好。所以本研究使用非结构化协方差对随机效应模型进行拟合计算。
3.2 枝条叶面积模型的检验和评价
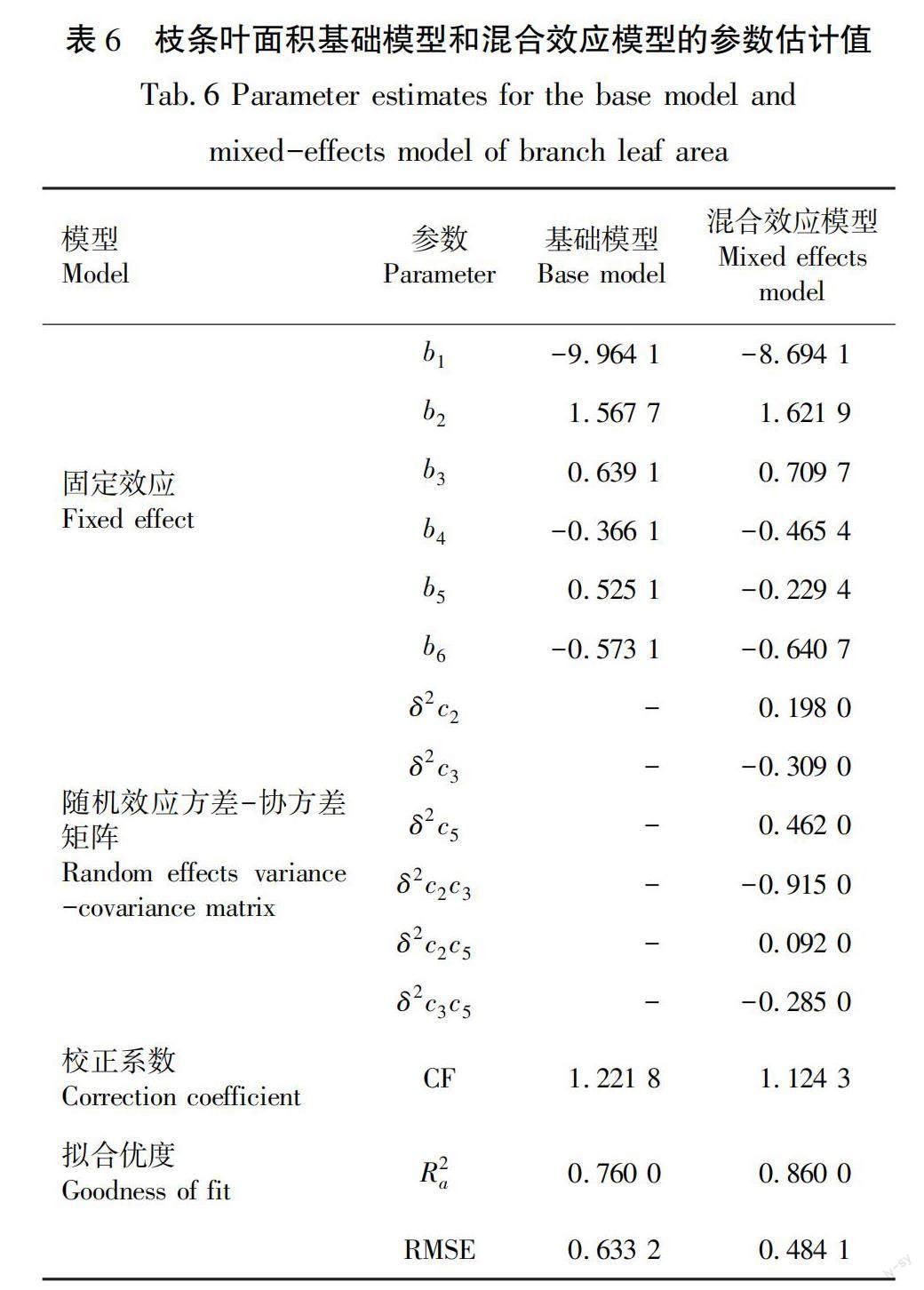
表6为红松一级枝条叶面积的基础线性回归模型和混合效应回归模型的参数估计值和统计指标数值。
由表6可知,混合模型的R为0.860 0,在基础模型(R=0.760 0)之上提高了约13%;混合效应模型的RMSE为0.484 1,比建立的基础线性模型(RMSE=0.633 2)缩小了0.149 1,约24%,说明本研究中前期建立的基础模型在加入随机效应成为混合效应模型后拟合效果得到优化,可以更精准地解释枝条叶面积的变化。
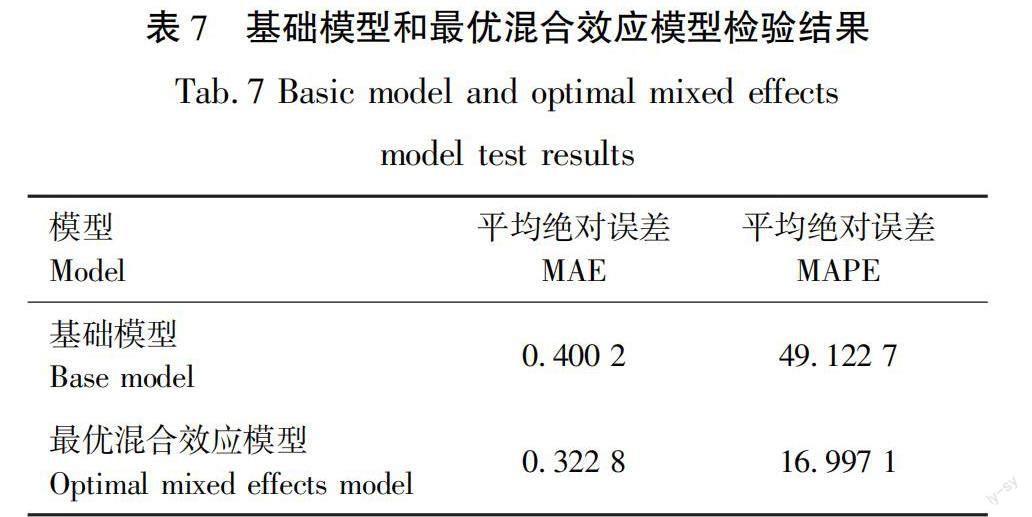
后使用随机抽取的独立检验数据分别对基础线性模型式(5)和最优混合效应模型式(6)进行检验,结果见表7。从表7中数据可知,尽管基础模型的MAE值和MAPE值已经处于较高水平,但是混合模型在此基础上均分别缩小了约19%和65%。
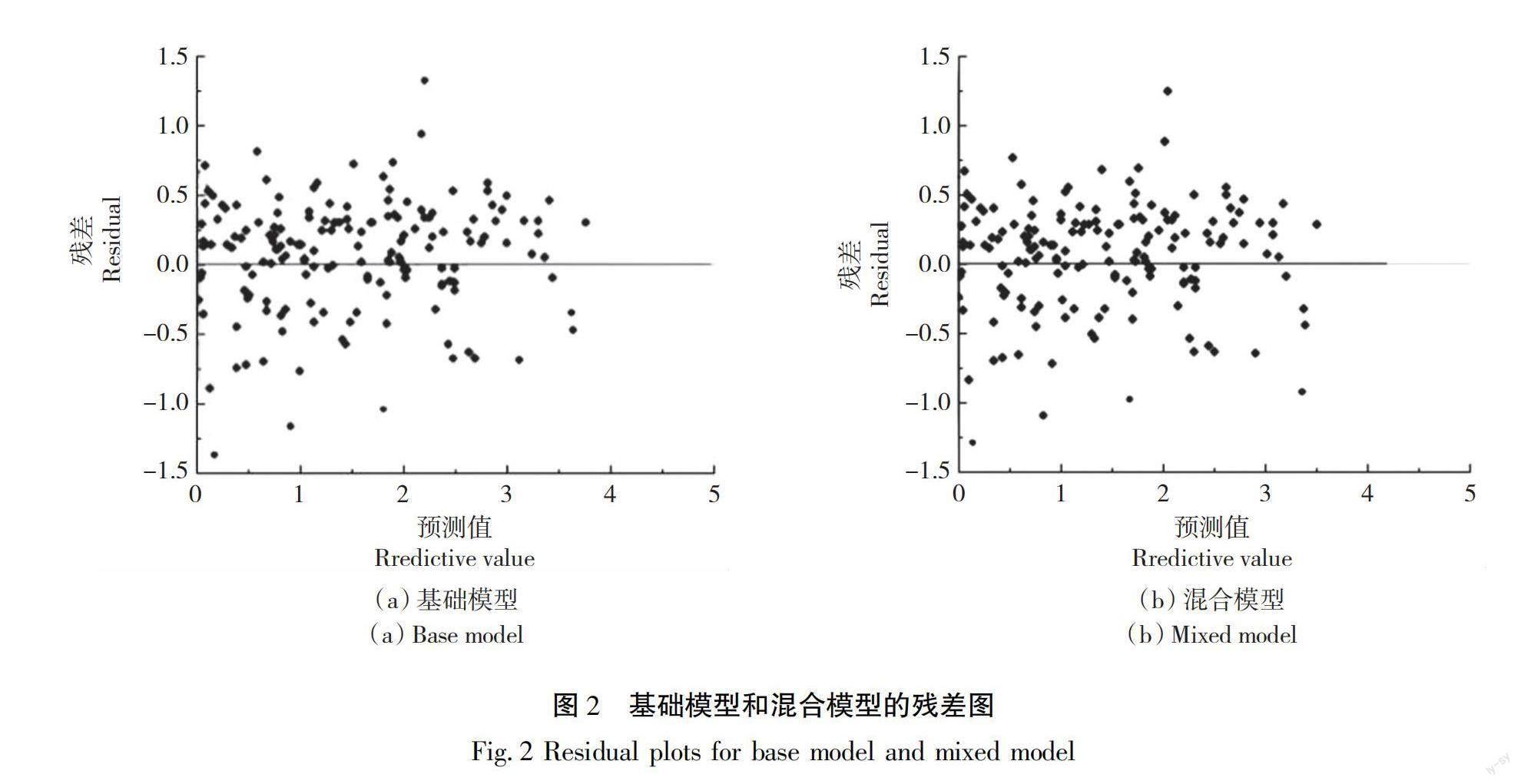
同时对于基础线性模型和最优混合模型使用统计软件画出残差图,如图2所示。由图2查看方差异质性,无明显喇叭状即没有异方差,模型得到了较好的拟合。
综上所述,本研究建立的混合效应模型的拟合效果和预估精度均比基础模型有所提高。
3.3 树冠叶面积混合模型的建立
将胸径、树高、冠长和高径比等作为自变量,带入基于Maguire等所提出的树冠叶面积模型中,使用R软件进行不同组合情况下的模型拟合,根据所得模型的R(越接近1越好)和RMSE(越小越好)进行选择,最后得出拟合效果最好的模型作为红松树冠叶面积的基础预估模型,模型如下。
式中:g—g为模型待估计参数;D為胸径。
在前文对枝条叶面积基础模型构建中已知非线性方程的拟合效果受参数的初始值影响,且不易收敛,对后期的模型优化具有较大影响,所以使用对数转换后得到如下模型
式中:g=lng;ε为误差项,其他参数意义同上。
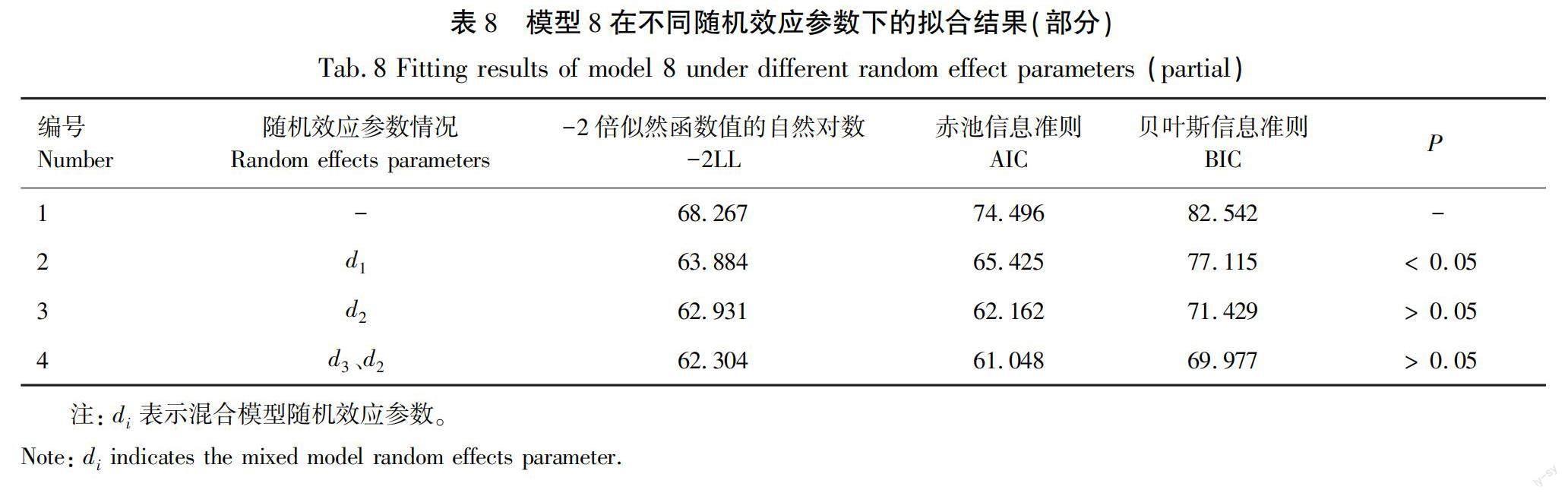
在红松树冠叶面积模型计算中,可以参照前文对枝条叶面积模型构建中引入随机效应的方法,以提高模型拟合优度,见表8。
由表8可知,1号模型和2号模型具有极显著差异(P<0.05),2号模型和3号模型差异为不显著(P>0.05),3号模型与4号模型对比同样不具有显著差异(P>0.05)。再经过对比AIC、BIC与-2LL这3个评价指标的数值,得出模型拟合效果最好的为2号模型,其模型具体表现形式如下。
3.4 树冠叶面积模型检验和评价
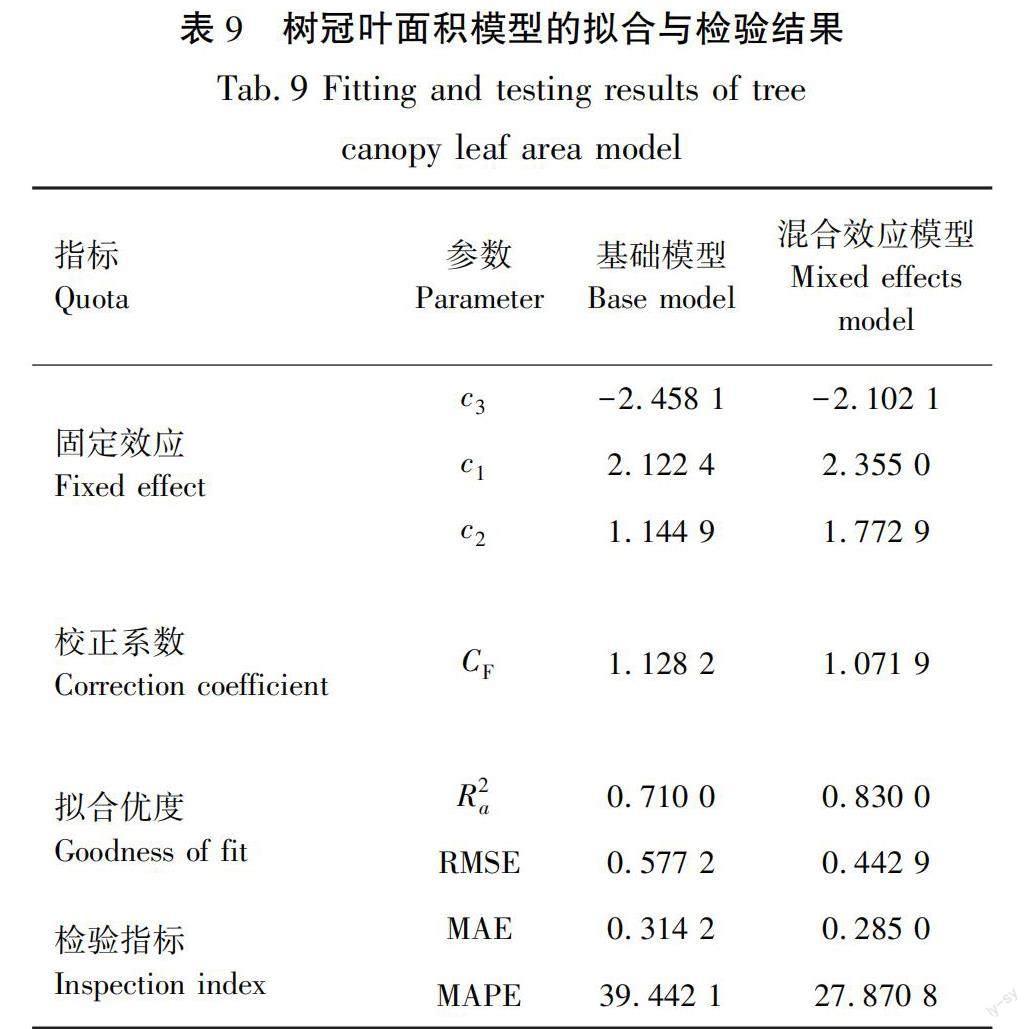
将表3中的建模数据带入基础模型中进行拟合计算,得到的参数估计值和相关指标见表9,由表9中数据发现,混合模型的为0.830 0,在基础模型(0.710 0)之上提高了约17%;混合模型的MAE为0.285 0,也在基础模型(MAE=0.314 2)的基础上减小了约9%;混合效应模型的RMSE为0.442 9,比建立的基础线性模型(RMSE=0.577 2)缩小了0.134 3,约23%,说明本研究中前期建立的基础模型在加入随机效应成为混合效应模型后拟合效果得到优化,可以更精准地解释树冠叶面积的变化。
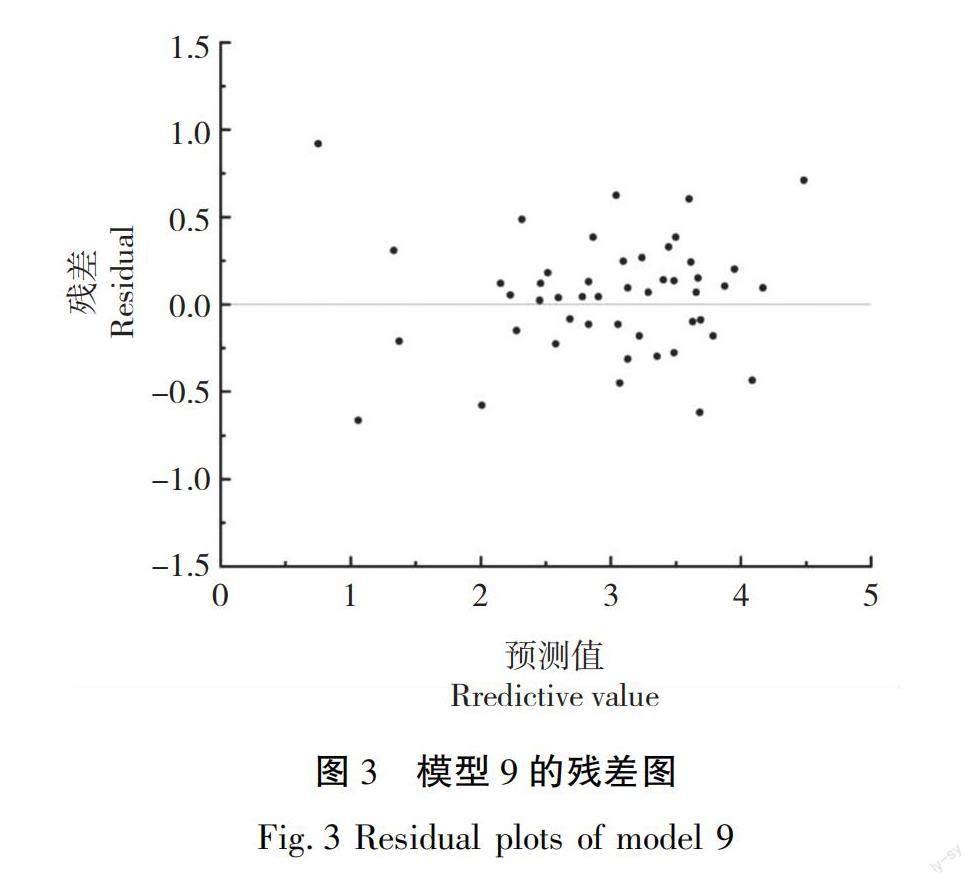
图3是将模型9带入最终参数估计值后做出的残差分布图,从图9中可见残差均匀分散在y=0的两侧,并未显现出显著的异常情况。
本研究将树冠叶面积模型作为具有不同胸径和冠长率的红松单株叶面积大小的模拟。根据得到的最终模型可知,在红松胸径相同时,具有更大冠长率的红松其叶面积总和也更大,当胸径变大时,具有更高冠长率的红松叶面积增加速度高于冠长率较低的红松;在冠长率相同时,具有更大胸径的红松其叶面积总和也更大,当冠长率变大时,具有更大胸径的红松的叶面积增加速度高于胸径较小的红松。
4 讨论
关于叶面積的研究在对树木生长能力的分析中起到了至关重要的作用,对如何促进树木的良好健康生长起到了指导性的作用;同样关于叶面积模型的构建和拟合优化也在逐步成为叶面积研究中的重中之重。
通过本研究可得:基于进行对数转化后的基础线性模型拟合效果较为良好,即以枝条枝长、基径、相对着枝深度、高径比和冠长率的对数形式为自变量的基础模型。随即在向该模型中引入随机效应时,发现在模型收敛的前提下,引入任意数量的随机效应参数都可以在原基础线性模型的基础上提高拟合效果,在对共63种随机参数组合的计算中,当随机参数个数为3时,混合效应模型达到了最好的拟合效果和拟合精度,即枝条长度、相对着枝深度、冠长率的对数形式为随机效应的参数组合,这与文献[27-31]的研究结论比较相似。经过计算可知混合效应模型的RMSE值较基础模型减小了约10.96%;R则比基础模型提高了约14.47%,后使用独立检验数据进行计算混合效应模型的各项指标均较基础模型有所改善,故本研究将上述混合模型作为枝条叶面积最优混合效应模型。
使用枝条求和法对单木层次的红松叶面积进行计算,由于在枝条叶面积模型拟合中可知引入随机效应可使模型拟合效果更好,所以在拟合树冠叶面积模型时也引用了样地层次的随机效应,最终得到的最优混合效应模型含有1个随机效应参数,混合模型的R为0.830 0,RMSE为0.442 9。通过检验结果可知该模型可以较好地对红松树冠叶面积进行预估计算。在红松胸径相同时,具有更大冠长率的红松其叶面积总和也更大,当胸径变大时,具有更高冠长率的红松的叶面积增加速度高于冠长率较低的红松;在冠长率相同时,具有更大胸径的红松其叶面积总和也更大,当冠长率变大时,具有更大胸径的红松的叶面积增加速度高于胸径较小的红松。
本研究中在对叶面积数据的获取上使用了排水法,排水法虽然在测量样本较多的红松针叶时具有快捷且方便的优点,但是仍然在手工测量叶片长度和排水体积时具有不可避免的误差因素。在以往对于使用排水法获取叶面积数据的研究中没有体现该种误差所带来的影响,笔者认为这种误差会随着基础模型的构建被传递进来,所以本研究在模型构建中引入随机效应以提高模型的拟合效果和拟合精度,尽可能地使模型的误差得到有效的缩小。
另外本研究所计算拟合的叶面积预估模型没有表现出红松叶面积的垂直分布规律,由于红松的横截面生长和边材液体流动的辐射格局等都与垂直分布息息相关,研究垂直分布规律可更好地揭示红松生长的诸多问题,具有较高的研究意义。因此,笔者认为基于本研究所得的红松叶面积的预估模型能够对红松树冠内部的垂直分布相关问题进行研究,可以更好地为我国红松经营和研究提供帮助。
【参 考 文 献】
[1]MONSERUD R A, MARSHALL J D. Allometric crown relations in three northern Idaho conifer species[J]. Canadian Journal of Forest Research, 1999, 29(5): 521-535.
[2]XIAO C W, JANSSENS I A, YUSTE J C, et al. Variation of specific leaf area and upscaling to leaf area index in mature Scots pine[J]. Trees, 2006, 20(3): 304-310.
[3]MOKHTARPOUR H, TEH C B, SALEH G, et al. Non-destructive estimation of maize leaf area, fresh weight, and dry weight using leaf length and leaf width[J]. Communications in Biometry and Crop Science, 2010, 5(1): 19.
[4]HAMMER G. Estimation of cassava leaf area by a simple, non-destructive field technique[J]. Journal of the Australian Institute of Agricultural Science, 1980, 46: 61-62.
[5]SADYKOVA G A, HANTEMIROVA E V, POLEZHAEVA M A, et al. Genetic variability of tree junipers of section Sabina: data from Dagestan, Armenia, and Crimea[J]. Russian Journal of Genetics, 2021, 57(10): 1223-1228.
[6]才志行.红松人工幼林针叶面积测定方法的探讨[J].林业科技,1980,5(3):30-33.
CAI Z H. Discussion on determination method of needle area of young Korean pine plantation[J]. Forestry Science and Technology, 1980, 5(3): 30-33.
[7]ZELLERS C E, SAUNDERS M R, MORRISSEY R C, et al. Development of allometric leaf area models for intensively managed black walnut (Juglans nigra L.)[J]. Annals of Forest Science, 2012, 69(8): 907-913.
[8]NYGREN P, REBOTTARO S, CHAVARRíA R. Application of the pipe model theory to non-destructive estimation of leaf biomass and leaf area of pruned agroforestry trees[J]. Agroforestry Systems, 1993, 23(1): 63-77.
[9]馮冬霞,施生锦.叶面积测定方法的研究效果初报[J].中国农学通报,2005,21(6):150-152,155.
FENG D X, SHI S J. Research on night measurement methods of leaf area[J]. Chinese Agricultural Science Bulletin, 2005, 21(6): 150-152, 155.
[10]柏军华,王克如,初振东,等.叶面积测定方法的比较研究[J].石河子大学学报(自然科学版),2005,23(2):216-218.
BAI J H, WANG K R, CHU Z D, et al. Comparitive study on the measure methods of the leaf area[J]. Journal of Shihezi University (Natural Science), 2005, 23(2): 216-218.
[11]柯娴氡,古丽红,周艳玲.阔叶树叶面积测量方法的比较和评价[J].广东林业科技,2006,22(4):96-99.
KE X D, GU L H, ZHOU Y L. A comparative evaluation of four methods for the determination of leaf area[J]. Guangdong Forestry Science and Technology, 2006, 22(4): 96-99.
[12]许易梅,刘红昌,徐松,等.白木通4份种质叶片形态差异及叶面积反演模型研究[J].西部林业科学,2022,51(4):116-124,133.
XU Y M, LIU H C, XU S, et al. Leaf morphological difference and retrieval model of leaf area for Akebia trifoliata var. australis[J]. Journal of West China Forestry Science, 2022, 51(4): 116-124, 133.
[13]WEISKITTEL A R, KERSHAW J A, HOFMEYER P V, et al. Species differences in total and vertical distribution of branch- and tree-level leaf area for the five primary conifer species in Maine, USA[J]. Forest Ecology and Management, 2009, 258(7): 1695-1703.
[14]MUNRO D D. Use of logarithmic regression in the estimation of plant biomass: discussion[J]. Canadian Journal of Forest Research, 1974, 4(1): 149.
[15]ZENG W S, TANG S Z. Bias correction in logarithmic regression and comparison with weighted regression for nonlinear models[J]. Nature Proceedings, 2011: 1.
[16]董利虎,李凤日,贾炜玮.基于线性混合效应的红松人工林枝条生物量模型[J].应用生态学报,2013,24(12):3391-3398.
DONG L H, LI F R, JIA W W. Linear mixed modeling of branch biomass for Korean pine plantation[J]. Chinese Journal of Applied Ecology, 2013, 24(12): 3391-3398.
[17]NI C C, NIGH G D. An analysis and comparison of predictors of random parameters demonstrated on planted loblolly pine diameter growth prediction[J]. Forestry: an International Journal of Forest Research, 2012, 85(2): 271-280.
[18]BUDHATHOKI C B, LYNCH T B, GULDIN J M. Nonlinear mixed modeling of basal area growth for shortleaf pine[J]. Forest Ecology and Management, 2008, 255(8/9): 3440-3446.
[19]JIANG L C, LI Y X. Application of nonlinear mixed-effects modeling approach in tree height prediction[J]. Journal of Computers, 2010, 5(10):1575-1581.
[20]臧颢,雷相东,张会儒,等.红松树高-胸径的非线性混合效应模型研究[J].北京林业大学学报,2016,38(6):8-16.
ZANG H, LEI X D, ZHANG H R, et al. Nonlinear mixed-effects height-diameter model of Pinus koraiensis[J]. Journal of Beijing Forestry University, 2016, 38(6): 8-16.
[21]KENEFIC L S, SEYMOUR R S. Leaf area prediction models for Tsuga canadensis in Maine[J]. Canadian Journal of Forest Research, 1999, 29(10): 1574-1582.
[22]苗铮,董利虎,李凤日,等.基于GLMM的人工林红松二级枝条分布数量模拟[J].南京林业大学学报(自然科学版),2017,41(4):121-128.
MIAO Z, DONG L H, LI F R, et al. Modelling the vertical variation in the number of second order branches of Pinus koraiensis plantation trees through GLMM[J]. Journal of Nanjing Forestry University (Natural Sciences Edition), 2017, 41(4): 121-128.
[23]MAGUIRE D A, BENNETT W S. Patterns in vertical distribution of foliage in young coastal Douglas-fir[J]. Canadian Journal of Forest Research, 1996, 26(11): 1991-2005.
[24]李凤日.长白落叶松人工林树冠形状的模拟[J].林业科学,2004,40(5):16-24.
LI F R. Modeling crown profile of Larix olgensis trees[J]. Scientia Silvae Sinicae, 2004, 40(5): 16-24.
[25]吴玉德,张鹏.基于Mapinfo的树木叶面积测定方法[J].林业调查规划,2005,30(6):23-25.
WU Y D, ZHANG P. The method for determining the leaf area of trees in view of Mapinfo[J]. Forest Inventory and Planning, 2005, 30(6): 23-25.
[26]NYGREN P, REBOTTARO S, CHAVARRIA R. Application of the pipe model theory to non-destructive estimation of leaf biomass and leaf area of pruned agroforestry trees[J]. Agroforestry Systems, 1993, 23(1): 63-77.
[27]WEISKITTEL A R, KERSHAW J A, HOFMEYER P V, et al. Species differences in total and vertical distribution of branch- and tree-level leaf area for the five primary conifer species in Maine, USA[J]. Forest Ecology and Management, 2009, 258(7): 1695-1703.
[28]ZELLERS C E, SAUNDERS M R, MORRISSEY R C, et al. Development of allometric leaf area models for intensively managed black walnut (Juglans nigra L.)[J]. Annals of Forest Science, 2012, 69(8): 907-913.
[29]邱思玉,孫玉军.长白落叶松人工林单木冠幅模型[J].东北林业大学学报,2021,49(2):49-53.
QIU S Y, SUN Y J. Individual tree crown width prediction models for Larix olgensis plantation[J]. Journal of Northeast Forestry University, 2021, 49(2): 49-53.
[30]郭孝玉.长白落叶松人工林树冠结构及生长模型研究[D].北京:北京林业大学,2013.
GUO X Y. Crown structure and growth model for Larix olgensis plantation[D]. Beijing: Beijing Forestry University, 2013.
[31]DAS N. Modeling develops to estimate leaf area and leaf biomass of Lagerstroemia speciosa in West Vanugach Reserve Forest of Bangladesh[J]. ISRN Forestry, 2014, 2014: 1-9.
