接触式轮廓仪测量的自动标注问题探究——基于最小二乘法

蒋培军

（三门峡职业技术学院 汽车学院，河南 三门峡 472000）

0 引言

轮廓测量仪作为一种精密设备常用于测量各种机械零件的截面轮廓形状和素线形状[1]。如在机械行业中，用于测量不同零件的线轮廓度、角度、直线度和平行度等；在汽车制造行业中，用于测量齿轮及油泵油嘴形状、汽车活塞外形等。接触式轮廓仪具有测量速度快，操作方便，结果可靠等优点，并且对于复杂工件也可实现测量。但是，由于存在探针缺陷、探针粘尘及扫描位置偏移等问题，易导致测量的轮廓曲线粗糙，影响工件形状的精确标注[2]。因此，利用测量数据建立数学模型，并对工件形状进行准确标注有重要意义。

1 接触式轮廓仪的测量原理及测量数据

图1 是一种常用的接触式轮廓仪，其结构包括固定架、可调三维平台、传感器、探针等部件。接触式轮廓仪为接触测量，通过仪器的触针与被测表面的滑移实现对被测物的测量[3]。轮廓仪传感器通过感知被测物表面的几何变化，在两个维度分别采点，并将采集的信息转换成电信号，再将电信号处理转换为数字信号进行存储，实现对工件的测量[4]。

图1 接触式轮廓仪及其结构组成

表1 给出了接触式轮廓仪测量的某工件水平状态下的轮廓线部分数据，数据来源于2020 年中国大学生数学建模竞赛D 题附件。该工件的具体轮廓如图2。图2 中，工件轮廓线由圆弧段和直线段构成，且均为平面曲线。对该工件进行准确标注，需利用数学方法拟合出各段曲线的表达式并求出节点坐标，进而标注轮廓线各项参数值[5]，如槽口宽度（x1，x3等）、圆弧长度、水平线段长度（x2，x4等）、圆心之间的距离（c1，c2等）、圆弧半径（R1，R2等）、人字形线的高度（z1）和斜线线段长度、斜线与水平线之间的夹角（∠1，∠2 等）。

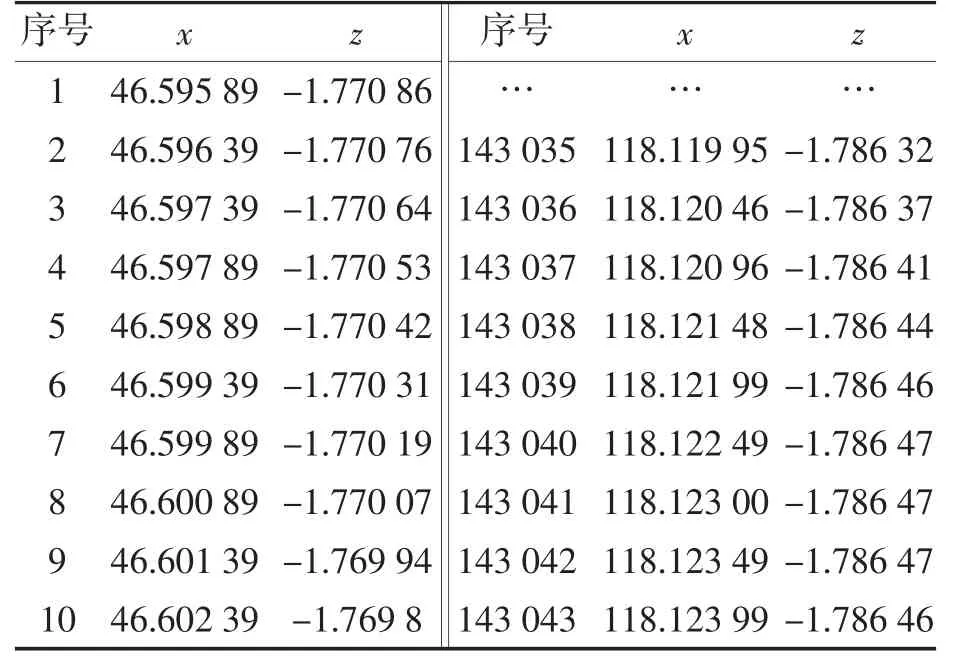
表1 接触式轮廓仪测量某工件轮廓部分数据

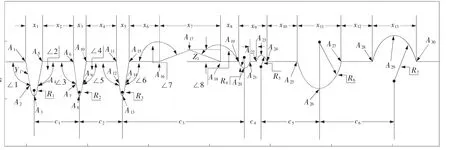
图2 工件轮廓

2 轮廓仪标注模型构建

2.1 斜直线拟合

工件轮廓图虽已给出，但仍需要与接触式轮廓仪测量数据进行比对，以便确定工件轮廓线的具体坐标，完成对工件形状的自动标注[6]。借助MATLAB 软件，绘制轮廓仪测量数据散点图如图3，完成工件轮廓图与接触式轮廓仪测量散点图的比对[7]。由于该工件的轮廓线由圆弧段和直线段构成，而直线段又包含水平直线段（斜率为零）与斜直线段（斜率非零），因此只需分别对这三类轮廓线建立模型并求解，即可完成对工件形状的标注[8]。

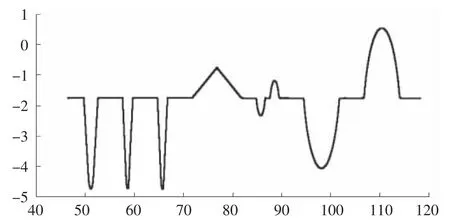
图3 接触式轮廓仪测量散点图

2.1.1 基于最小二乘法构建模型

由于种种原因，接触式轮廓仪对复杂工件测量时会出现轮廓线粗糙不平现象，需借助数学优化方法进行拟合后对其进行精确标注。最小二乘法通过误差平方和最小化寻找数据的最佳匹配函数，其目标是找到一组参数，使得拟合函数的预测值与实际观测值的差异最小[9]。作为一种经典的数学优化方法，最小二乘法可用于解决未知参数估计及曲线拟合等问题，也可用于其他优化问题。例如，能量最小化或熵最大化等均可通过将问题转化为最小二乘形式，应用最小二乘法来求解。因此，本文采用最小二乘法构建轮廓线的拟合模型。

对于工件轮廓中的斜直线段，以A4A5段为例，采用最小二乘法，建立斜直线拟合模型，其原理表达式为

其中，（xi，zi）为A4A5段轮廓仪测量数据，a，b 为待定参数。

由于节点A4和A5具体坐标未知，为便于模型拟合，选取A4A5段坐标的一个子区间段对斜直线模型式（2）进行拟合[10]。

式（2）中，ε 为随机误差项，且假设ε 满足最小二乘模型对误差项的基本要求。为了让更多的测量点进入模型，结合图3，选择[52，52.5]区间段数据对A4A5段斜直线方程进行拟合。

对比轮廓仪测量数据，序号10 763—11 790共1 028 组数据在[52，52.5]区间段，将其作为样本点，借助MATLAB 软件[11]即可求得A4A5段拟合方程为

2.1.2 模型误差项检验

对斜直线拟合模型及误差项进行检验[12]，得到模型拟合优度为0.999 3，说明因变量的99.93 %变异可由自变量的变异解释。模型F=1 498 817.76，对应概率P=0，在置信水平（1-α=0.95）下，表明模型通过显著性检验，建立的斜直线模型有统计学意义[13]。

图4 为斜直线模型误差检验图。由图4a）可以看出：斜直线模型误差随机分布在零点附近，在1 028 组数据中，有743 项残差在[-0.01，0.01]，占比72.28 %；有963 项残差在[-0.02，0.02]，占比93.68 %，表明模型整体拟合效果较好。序号为280—344 的样本点残差超过了0.02，对比样本点位置可知，该型号接触式轮廓仪在工件几何形状发生改变一小段距离后会产生较大的测量误差。

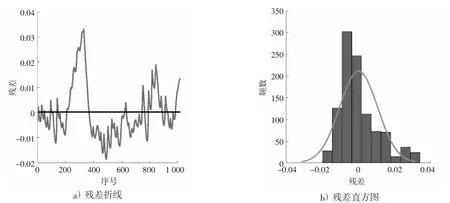
图4 斜直线模型误差检验结果

由图4b）的残差直方图可看出，误差项大致服从正态分布。为了定量化分析模型误差项是否服从正态分布，采用K-S 检验[14]对斜直线模型误差项进行分析。K-S 检验的原假设为H0，即斜直线模型误差项分布与正态分布无显著差异；备择假设为H1，即斜直线模型误差项分布与正态分布存在显著差异。由表2 可看出，斜直线模型误差项的K-S 检验统计量为4.122 2，对应的概率P=0.062 1>0.05，表示接受原假设，认为斜直线模型误差项分布与正态分布无显著差异，表明模型误差项满足最小二乘回归对误差项的基本要求[15]。

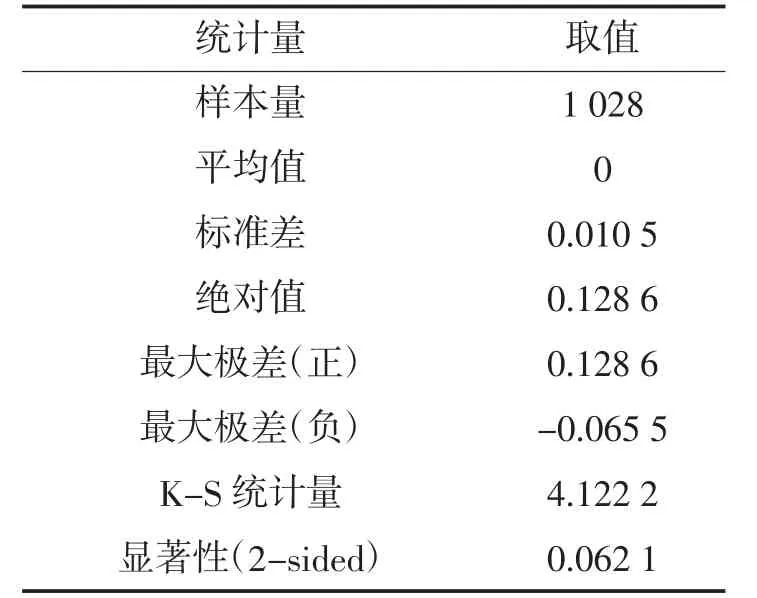
表2 斜直线模型误差项K-S 检验表

对于其他斜直线段如A6A7、A9A10、A17A18等，都可类似给出拟合模型并进行检验。求出斜直线拟合方程后，可利用式（4）求出斜线与水平线间的夹角。例如：∠2=π-arctan 2.782 7=1.915 8，即角度为109.766 8°。对于其他各角可类似求解，本文不再赘述。

2.2 水平直线段拟合

对于工件中的水平直线段，以A5A6段为例，建立拟合模型。水平直线段可视作斜直线段斜率为零的一种特殊情况，对应的模型为

其中，c 为常数，其估计值为

对于A5A6段，选择[53，57]区间段轮廓仪测量数据对其进行拟合。根据接触式轮廓仪测量数据，找出x∈[53，57]的样本点，其序号为12 796—20 795，在此区间的样本点共有8 000 组，对其坐标zi求平均值，可得c^=-1.767 4。模型的显著性检验及误差项检验可参照2.1.2 节进行。对于其他水平直线段如A10A11、A15A16、A27A28等也可类似给出拟合模型。

2.3 圆弧段拟合

在平面直角坐标系中，圆的标准方程为

其变形式为

式（9）中D，E，F 为待定参数。

接触式轮廓仪测量数据中，序号为8 531—9 729共计1 199 组数据在[50.9，51.5]区间段，将其作为样本点，借助MATLAB 软件中的非线性拟合函数[17]，求得段的拟合圆方程为

此外，工件的节点为斜直线段、水平直线段和圆弧段的交点，在已知轮廓曲线方程的情况下可以通过联立方程组求解节点坐标。如对节点A5可联立方程组为

由方程组（11）求得A5坐标为（52.658 4，-1.767 4）。其他节点坐标可类似求取。

3 模型的推广与不足

接触式轮廓仪自动标注模型的构建，是最小二乘法在机械加工领域的一项应用探索。经验证，构建的模型可实现接触式轮廓仪测量数据的校准，精确标注被测工件的各项参数，对接触式轮廓仪的推广及后续设计有积极作用。但是，模型建立也存在一些不足：

1）在各段轮廓线拟合时，采用对比法截取拟合数据区间段，存在一定的主观性，会对模型精度产生影响；

2）只对圆弧段和直线段轮廓线建立了轮廓仪标注模型，对于其他曲线段轮廓线如何标注未做讨论；

3）模型的误差项中可能存在一些有价值的信息，还需进一步研究采用合适模型对误差项信息进行提取，以进一步提高模型精度。

4 结束语

作为一种精密设备，接触式轮廓仪在机械零件的截面轮廓形状和素线形状的测量中应用广泛。为减少轮廓仪测量工件的轮廓曲线粗糙情况，更好地对工件形状进行标注，针对数学建模大赛赛题提供的轮廓仪测量数据，基于最小二乘法对测量数据中的圆弧段和直线段轮廓线建立了标注模型。模型显著性检验及误差项检验显示，提出的轮廓仪标注模型符合对随机误差项的基本假设，建立的模型具有统计学意义。轮廓仪测量数据与标注后数据进行拟合的效果对比表明，模型能一定程度上解决工件形状不能准确标注的问题。