基于回归分析的沿海不同重现期波浪参数换算关系研究

夏运强，闫志铎，赵雪夫

（中国人民解放军91053 部队，北京 100070）

0 引言

重现期波浪是港口工程和海洋工程一个重要设计参数，定义为出现超过已知水平的暴风浪的平均时间间隔，单位为年（a）[1]，它是设计波浪标准（包括重现期和波列累积频率）两个要素之一。现行JTS 141—2011《水运工程设计通则》[2]和JTS 145—2015《港口与航道水文规范》[3]规定了永久性水工建筑物结构强度和稳定性计算波浪重现期一般采用25～100 a，临时性建筑物波浪重现期一般采用5～10 a，校验港池水域平稳度的设计波浪一般采用2 a 一遇。重现期波浪参数包括重现期波高和对应的重现期波周期。

现行《港口与航道水文规范》[3]对重现期波浪只是提供了计算原则和方法，即通过收集具体工程地点历史实测或后报波浪数据（主要是年最大值）组成样本序列，对其进行频率分析，确定不同重现期的设计波浪参数；波高和周期的频率曲线可采用P-Ⅲ曲线，有条件时，也可根据与实测资料拟合最佳的原则，选配极值Ⅰ型分布、对数正态分布和威布尔等其他的理论频率曲线，确定不同重现期的设计波浪；对于台风多发海区，某一波向1 a 中出现1 个以上较大台风波高时，可按台风波高的最大值系列取样，采用泊松-冈贝尔复合极值分布确定不同重现期的设计波浪。尤再进[4]基于对比现行规范提出了波高统一化计算方法，罗耀等[5]提出了基于超定量概率模型的重现期波高计算方法，陈汉宝等[6]讨论了国内外行业规范对波浪重现期和设计使用年限的规定和相互关系，宋伟伟等[7]基于SWAN 台风后报模型推算了外海重现期波浪要素，与实测数据对比吻合较好，邓兆青等[8]同样采用SWAN后报模型推算给出渤海湾4个代表点位5～100 a 重现期波高，高文达[9]对规范提供的短期测波资料分析重现期波高提出了改进建议，王少平等[10]证明了采用P-G 复合极值分布曲线较PⅢ型频率曲线的优势。水文规范[3]的附录M 提供了沿海部分水域重现期波浪要素推算参考值，涵盖了自北向南共计12 个海洋站。另外，水文规范提供了各种累积频率波高间的换算关系式，参照此种表达方式，提供一种便捷的、具有一定精度和通用性的不同重现期波浪参数之间的近似换算关系，为工程应用和相关课题研究提供必要的基础波浪资料。

1 技术路线

针对大陆沿海，通过收集尽可能多的各站点重现期的波浪数据，汇总建立数据库，进行数据统计分析，建立不同重现期波浪参数之间的换算关系。

具体步骤：以2 a 一遇波浪数据（波高和周期）为基数，分别计算5 a、10 a、25 a、50 a、100 a波浪数据与2 a 数据比值，对所有比值数据汇总后进行样本回归分析和误差分析[11]，最终得到具有一定普适性的沿海重现期波浪换算关系。

统计分析涉及的参量包括平均值MN、标准差SD、离散系数CV，其中：平均值MN 为算术平均值，是反映样本数据集中趋势的一项指标；标准差SD 又称为标准偏差，是样本方差的算术平方根，它反映数据的离散程度，是表示精确度的重要指标，适合于平均值MN 相同时的样本集的比较；离散系数CV 定义为标准差SD 与平均值MN 的比值，同样可反映数据集的离散（变异）程度，它适用于平均值不同时的样本集的比较。

回归分析采用一元非线性回归分析方法，并采用t 检验法对相关系数R 进行显著性检验，评估其回归拟合效果。

2 样本统计分析及结果

2.1 样本数据库建立

收集到的波浪重现期数据共有11 个站位，包括渤海3 个站位（老虎滩、芷锚湾、天津港），黄海2 个站位（小麦岛、连云港），东海4 个站位（嵊山岛、大陈岛、南麂、崇武），南海2 个站点（大万山、涠洲岛），东海长江口站位数据不全，未采用。数据处理以老虎滩站点例举见表1 和表2，表中，H1/10定义为1/10 大波波高，T 定义为平均周期。

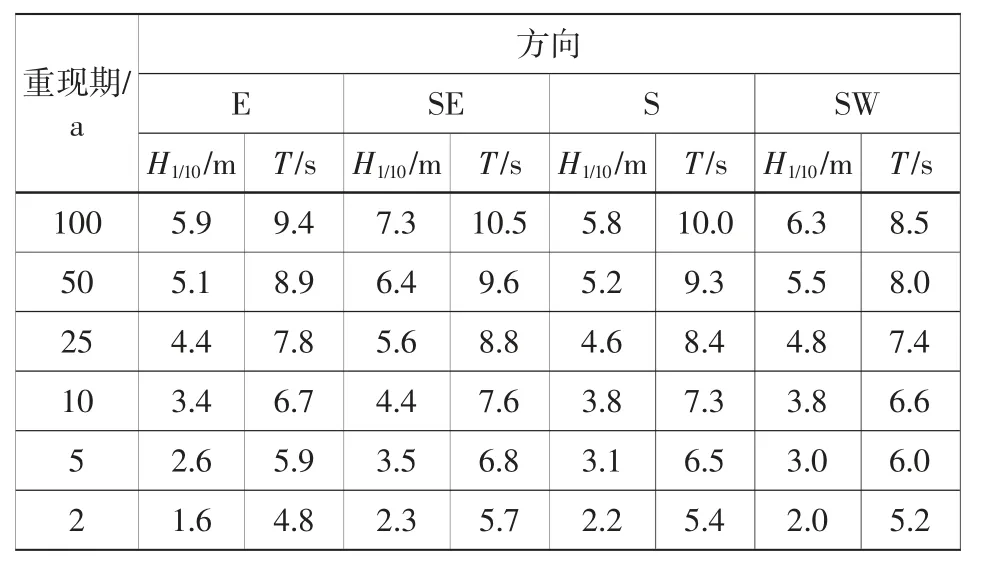
表1 老虎滩海洋站重现期波要素Table 1 Return period wave elements in Laohutan ocean station

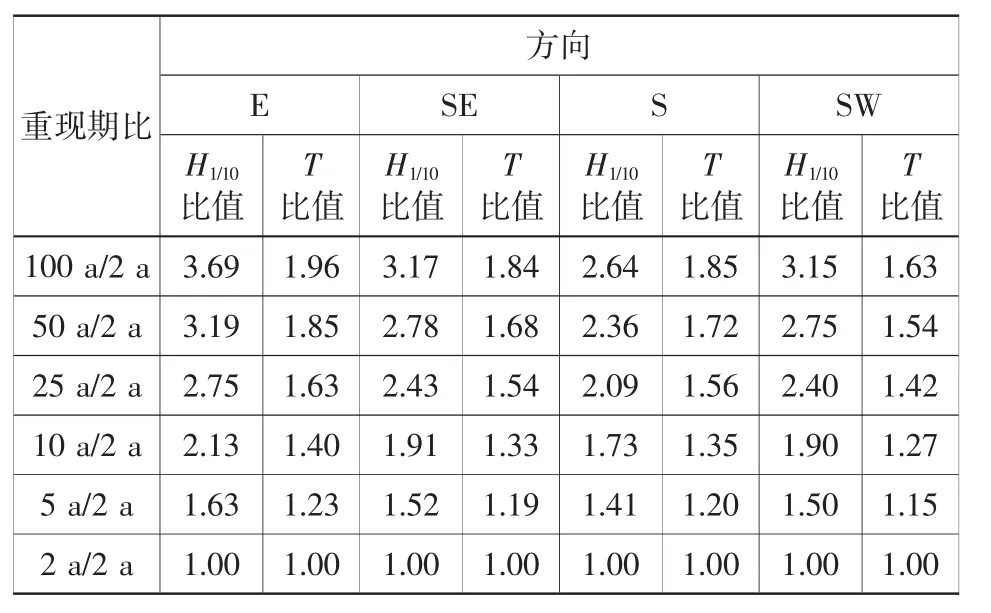
表2 老虎滩海洋站波浪数据换算Table 2 Wave data conversion in Laohutan ocean station

2.2 汇总分析及结果

波要素包括波高和波周期，得到不分波向共计71 组数据组成有效样本。对样本进行统计分析，计算其平均值、标准差和离散系数。结果见表3 和表4。

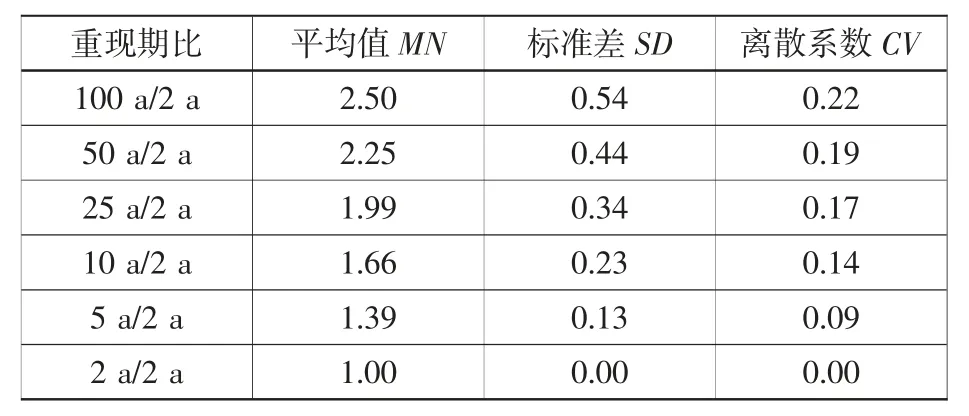
表3 沿海波浪波高比值统计结果Table 3 Statistical results of wave height ratio in coastal

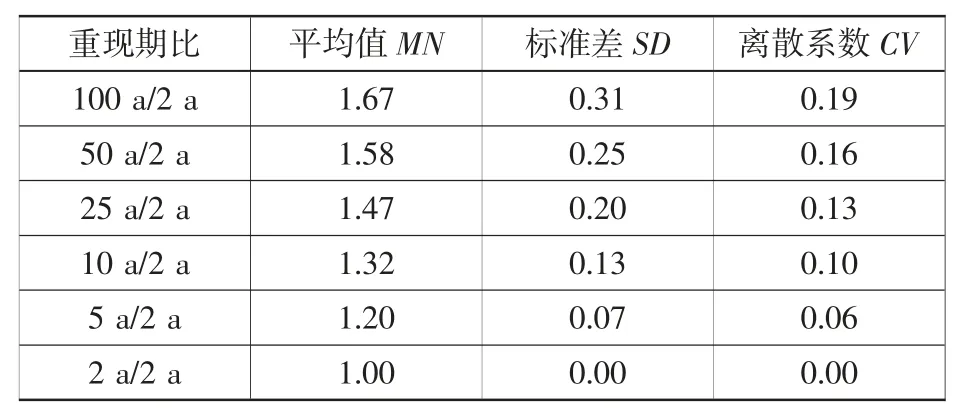
表4 沿海波浪周期比值统计结果Table 4 Statistical results of wave period ratio in coastal

分别以波高比和周期比的平均值为纵坐标，以2 a 一遇为基数的重现期比为横坐标，进行回归分析（趋势线拟合），得到沿海波浪波高比y1-重现期比x 和周期比y2-重现期比x 的关系曲线，见图1 和图2。

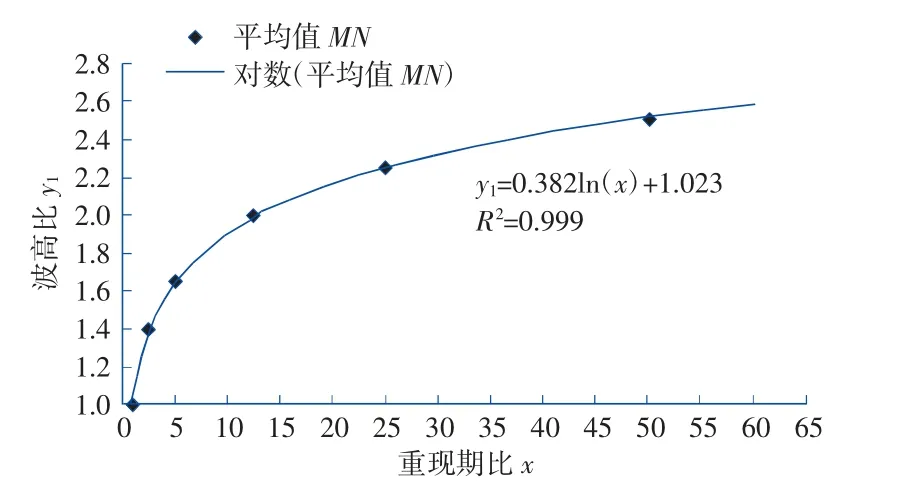
图1 沿海波浪波高比y1-重现期比x 关系拟合图Fig.1 Fitting diagram of the relationship between wave height ratio y1 and return period ratio x in coastal

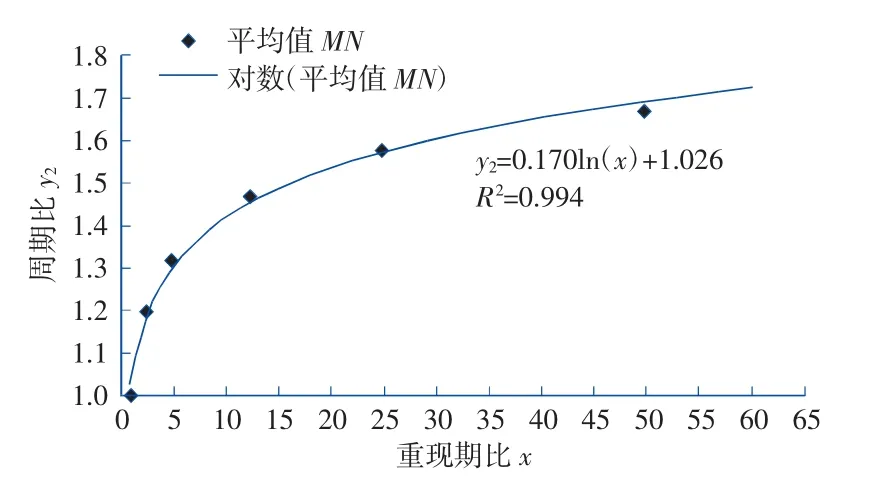
图2 沿海波浪周期比y2-重现期比x 关系拟合图Fig.2 Fitting diagram of the relationship between wave height ratio y2 and return period ratio x in coastal

分析上述图表，可见：

1） 波浪波高比y1-重现期比x 关系符合对数分布曲线，其近似换算关系式为：

相关系数R=0.999（R2=0.999），采用t 检验法对相关系数进行显著性检验，n=6，查表，a=1%时，Rmin=0.917；a=5%时，Rmin=0.811，可知，该拟合曲线下波高比与重现期比间有高度显著相关关系。

常用重现期波高比近似换算关系式如下：

2） 波浪周期比y2-重现期比x 关系同样符合对数分布曲线，其近似换算关系式为：

相关系数R=0.997（R2=0.994），同样采用t 检验法对相关系数进行显著性检验，该拟合曲线下波浪周期比与重现期比间有高度显著相关关系。

常用重现期波周期比近似换算关系式如下：

3） 根据表中标准差SD 和离差系数CV 数值，随着重现期比的增大，波高比和周期比数据的离散程度均呈加大趋势。重现期25 a 以内的数据离差系数基本在0.15[11]以内，具有较为理想的精度。

后续可增加沿海工程实例站点重现期波浪数据，扩大数据库样本，采用上述技术路线，进一步优化其相关关系。也可以分海区进行所辖站点波浪数据统计分析，得到各海区不同重现期波浪参数换算关系。

3 结语

基于现行水文规范沿海11 个海洋站点的重现期波浪资料建立数据库，对样本进行统计分析，主要结论如下：1） 重现期波浪波高比y1和周期比y2与重现期比x 均具有高度显著相关性，其近似换算关系符合对数分布。2） 随着重现期比的增大，波高比和周期比数据的离散程度均呈加大趋势，重现期25 a 以内的参数换算具有较为理想的精度；3） 后续可增加工程实例的数据库样本，进一步优化其相关关系。