新电力市场下的全国发电量年度组合预测研究
2023-11-26郑桂博
刘 丹,陈 军,高 政,郑桂博,张 亮
(国家能源集团电力营销中心有限公司,北京 100010)
0 引 言
发电量预测作为电力行业中一个热点问题一直深受关注,特别是近些年异常气候增多,可再生能源发电存在较大的不确定性,电力保供难度加大,发电量中长期预测成为越来越重要的研究领域。精确、科学的预测是正确决策的前提和保证,发电量预测本质上是对电力市场供应的预测,在商业化的体制下,做好发电量预测尤其是中长期预测工作将直接关系到电力市场发电企业运行所需的成本与经济效益。
当前国内外的电力负荷预测方法研究相对成熟,预测发电量的方法多种多样,其中主要包括传统回归模型预测方法、时间序列预测方法以及人工神经网络预测方法。
回归模型预测技术是根据历史负荷数据资料,依靠线性回归数学模型对未来的负荷进行预测,研究各自变量和因变量之间的关系,形成回归方程[1]。随着日前交易市场和短期现货交易市场在美国和欧洲进行试点改革,各类技术进一步发展,时间序列模型组件成为发电量预测的重要方法。发电量序列属于典型的时间序列,而时间序列模型中的ARMA和指数平滑法应用最为广泛[2-3]。时间序列模型由于精度高、所需数据简单而被市场分析者和电网公司所青睐。时间序列模型将负荷数据看成是一个周期性变化的时间序列,然后根据给定的模型对未来的负荷进行预测。近些年来,越来越多的学者形成一种共识,即预测精度的提高必须要考虑其他因素对发电量预测的影响,很多智能预测算法如神经网络、支持向量机、专家系统、粒子群算法、遗传算法等开始大量地运用于发电量预测中,其中神经网络预测方法的应用最为广泛。BP神经网络是最基础且最为经典的预测方法,诸多神经网络预测文献表明,神经网络预测方法在精度方面通常优于传统的线性回归模型和时间序列预测方法。
国内学者在预测过程中,早期多借鉴专家经验和各类预测模型,用于优化单一预测模型存在的缺点,通过将多种预测方法进行组合,按照协方差最小原则确定权数,形成最终的预测模型,从而在一定程度上提高预测精度。此外,由于中国特色社会主义经济制度的特点,电力供给更多承担着社会服务和民生保障的功能,因此当政策等宏观因素变动时,尤其是在保供时间的影响下,电力供需形势未必会按照市场规律进行调节,政策变化和保供要求将会为发电量预测带来较大的挑战。因此国内学者在进行发电量预测的过程中,十分注重宏观因素包括GDP、人口以及政策等的影响[4]。
文中分别选用改进的多元线性回归和BP神经网络预测对2000~2021年全国发电量数据进行分析,并且对未来10年全国发电量数据进行组合预测。
1 多元线性回归
1.1 模型描述
多元线性回归是建立多个自变量与因变量之间的定量关系,通过回归系数反映因变量对自变量的影响程度。在建立预测模型的过程中,假设问题的因变量为y,自变量即对因变量y产生影响作用的变量有n个,这n个变量分别是x1,x2,…,xn[5]。假设因变量y与其影响因素之间存在一定的定量线性关系,可写出如下的线性关系式:
y=β0+β1x1+β2x2+…+βnxn+a
(1)
式中:y为因变量;xi为自变量(i=1,2,3,…,n);β0为回归常数项;βi为回归系数(i=1,2,3,…,n);a为随机误差项[6]。
为了方便在建立模型的过程中进行估计,假设参数a服从正态分布,即参数a满足以下条件:
E(a)=0,D(a)=σ2<∞
(2)
式中:E(a)为随机误差的均值,D(a)为随机误差的方差,σ为随机误差项的标准差。
由此可以得到一个n元线性回归模型,即
(3)
1.2 发电量的初次回归
根据中国2010~2020年的用电量、GDP和人口数,首先初步建立线性回归模型, 在SPSS中对自变量和因变量进行线性回归分析,得到估计参数和显著性检验值,见表1。根据表1中的数据可以得到初步的线性表达式:
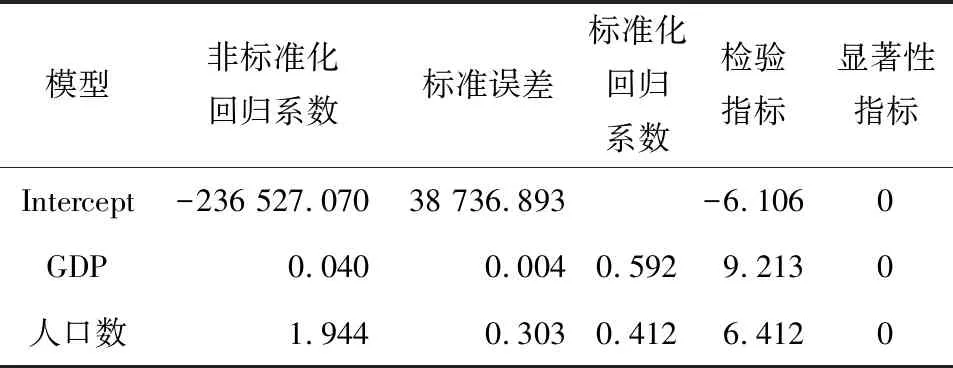
表1 初次线性回归估计参数
y=-236 527+0.039 8x1+1.944 0x2
(4)
回归方程(4)的显著性检验结果见表2。根据表2中显示的数据,回归方程的R2为0.995 9,这说明回归方程从整体上是显著的,但不代表回归方程中的每一项都是显著的。按照表1中的数据,由于在进行线性回归时设置的置信区间为95%,所以在显著性水平0.05以下,2个自变量均是显著的。

表2 回归方程整体的显著性检验结果
该模型中存在2个自变量,自变量之间可能存在一定的线性关系。如果各个变量之间存在严重的共线性关系,这时使用最小二乘法所得的方程有可能会无效,从而基于该方程进行分析可能会出错,甚至会引入歧途。这种情况被称为多重共线性问题,所以在分析的时候必须要作多重共线性诊断,才能得到较为合理的结果。
诊断所用的方法是看方差膨胀因子VIF的值落在哪个区间。方差膨胀因子VIF是指解释变量之间存在多重共线性关系时的方差与不存在多重共线性关系时的方差之比,是容忍度的倒数[7]。VIF越大,显示共线性程度越严重。通过方差膨胀因子可以考虑单个自变量与其他自变量的多元线性回归,从而计算自变量之间新模型的判定系数,记为r2,r2为以xi与其他自变量的复测定系数,方差膨胀因子VIF的计算式为
α=1/(1-r2)
(5)
α反映自变量之间线性关系的具体规则为:当α<5时,表示自变量之间共线性的程度不存在或很弱;若5≤α ≤10,表示自变量之间共线性程度为中等程度;若α>10,表示自变量之间存在严重的共线性程度[8]。
该问题中各个自变量之间方差膨胀因子计算结果见表3。

表3 方差膨胀因子α
通过比较诊断原则和表1~3中的数据可知,2个自变量GDP和人口数之间存在严重的共线性关系。
1.3 发电量的改进线性回归
根据计算方差膨胀因子,发现人口数与GDP之间存在严重的多重共线性,因此考虑将人口数变量或GDP变量剔除掉再次进行回归分析,重新建立线性回归模型,即再次使用SPSS进行线性回归,再次求取方程各项参数。
1.3.1 剔除人口数后的线性回归
将人口数剔除后,重新建立发电量与GDP之间的线性回归模型,各项参数见表4。
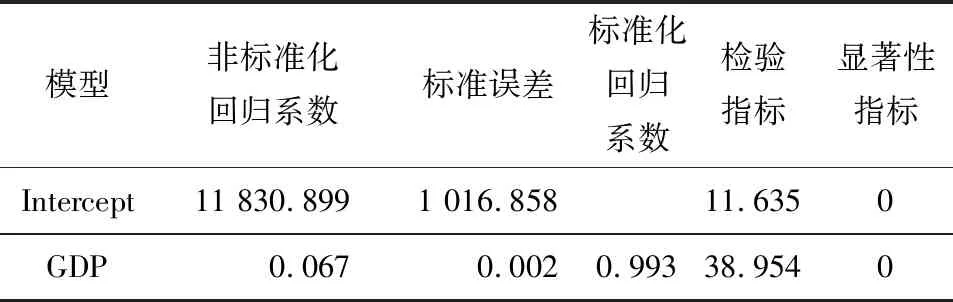
表4 剔除人口数后线性回归参数
根据表4中的数据,可写出改进后的线性回归方程如下:
y=11 830.899+0.067x1
(6)
改进后线性回归方程的整体显著性检验结果见表5。

表5 剔除人口数回归方程的显著性检验结果
根据表4中数据,在置信水平为0.05的情况下,目前自变量GDP通过了系数检验,而根据表5可知,线性回归方程的整体相关性为0.987。
1.3.2 剔除GDP后的线性回归
将GDP剔除后,重新建立发电量与人口数之间的线性回归模型,各项参数见表6。
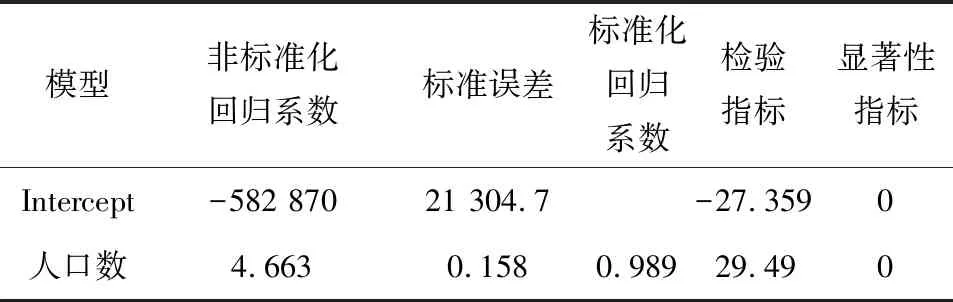
表6 剔除GDP后线性回归参数
根据表6中的数据,可写出改进后的线性回归方程如下:
y=-582 870+4.663x2
(7)
改进后线性回归方程的整体显著性检验结果见表7。

表7 剔除GDP回归方程的显著性检验结果
根据表6中数据,在置信水平为0.05的情况下,目前自变量人口数通过了系数检验,而根据表7可知,线性回归方程的整体相关性为0.978。
由此可见, GDP与发电量之间的线性回归模型拟合效果更好,故选取自变量GDP来预测未来10年的发电量情况,得到最终的线性回归方程为
y=11 830.899+0.067x1
(8)
式中:x1为GDP。
1.4 线性回归的预测实例
根据联合国经济和社会事务部2023年7月发布的《世界人口展望2022》预测,中国人口在2022年预计较2021年有所下降。根据国家信息中心预测,中国2022年GDP增速约为3.5%,2023年GDP增速约为5%。2020年9月,在中国宏观经济论坛举行的CMF宏观经济热点问题研讨会上,瑞银亚洲经济研究主管、首席中国经济学家汪涛在会上预测,未来10年,中国实际年均GDP增速将下降到4.5%。由此预测未来10年中国的人口数与GDP预测值见表8。
将2021~2030年的GDP数据带入式(6)中,得到2021~2030年的全国发电量数据见表9。
2 BP神经网络预测
2.1 BP神经网络模型描述
BP神经网络是一种正向前馈神经网络[9],利用最速梯度下降法的误差逆传播对网络权值和阈值进行不断修正[10],一直到终止条件满足为止。BP神经网络能学习和存贮大量的输入-输出模式映射关系,无需使用者具有描述这种映射关系的数学方程的相关知识,根据Kolmogorov的相关定理,可以由一个包括输入层(input)、隐含层(hidden layer)和输出层(output layer)的3层BP神经网络对非线性映射进行任意精度的逼近。从数学意义上讲,若输入层的节点数为n,输出层节点数为l,BPNN是从Rn到Rl的一个高度非线性映射,在所选网络的拓扑结构下,通过学习算法调整各神经元的阈值和连接权值使误差信号取值最小。图1所示的是一个典型的3层BP神经网络的网络拓扑结构[11]。从图1可以看出,BP神经网络的存储信息的结构可以分为2个部分:1)网络的体系结构,即网络输入层、隐含层和输出层神经元个数;2)相邻节点之间的连接权值。
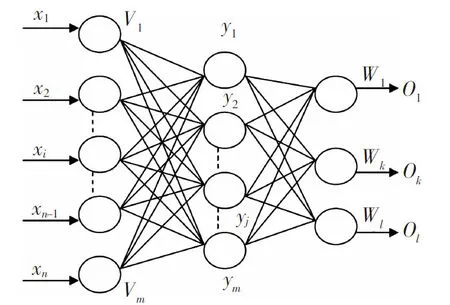
图1 3层BP网络拓扑结构示意图
以BP网络模型中的最后一层为例,通过计算各节点希望输出值与实际输出值之差的平方和Ep:
(9)
式中:P为BP网络模型中的最后一层;tpj为最后一层节点j的希望输出值;Opj为最后一层节点j的实际输出值;M为节点总数。
然后通过误差反向传播进行梯度链式求导的方式训练连接权重,从而得到最优的训练网络:
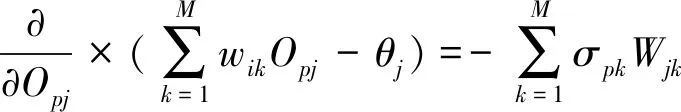
(j=1,2,…,m)
(10)
式中:Ipk为最后一层节点k的净输入;θj为节点的阈值;wik为节点j到k之间联系的权重。
2.2 BP神经网络模型的预测实例
利用Matlab中BP神经网络工具包,设置训练参数,其中隐藏神经元个数设置为15个,迭代次数为100次,训练目标为10-3,学习率为0.01,得到预测模型,利用验证集数据对预测模型进行验证,得到其预测结果如图2所示,且决定系数为0.990 7,可见其拟合效果良好。

图2 验证集预测值与实际值对比结果
结合BP神经网络,以2000~2021年全国发电量数据为基础,对历年及未来10年电力负荷进行预测,以检验该模型的精度,使对发电量的预测更有说服力,最终预测结果见表10。

表10 2022~2031年全国发电量BP神经网络预测结果
通过上述方法的预测以及相关的参数检验,得到2种方法的预测结果见表11。在此基础上,由于BPNN具有较好的非线性预测能力,而多元线性回归具有较好的线性拟合解释能力,因此取平均值对2种方法进行组合预测,最终得到表11。
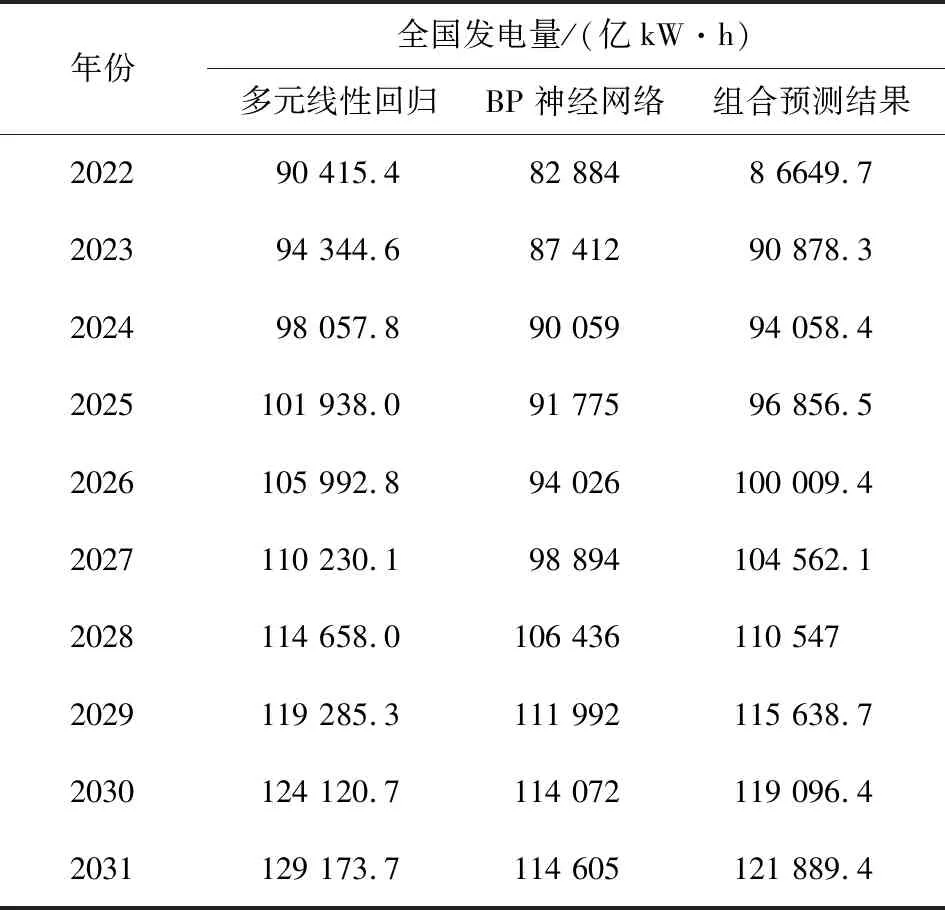
表11 不同预测方法下2022~2031年全国发电量预测值
2001~2022年全国发电量最终的组合预测值与实际值的对比如图3所示。

图3 实际值与预测值的对比
利用决定系数(r2)、平均绝对误差(MAE)和均方误差(RMSE)确定不同模型的拟合效果。将多元回归预测模型、BP神经网络预测模型以及组合预测模型的预测精度进行对比,见表12。
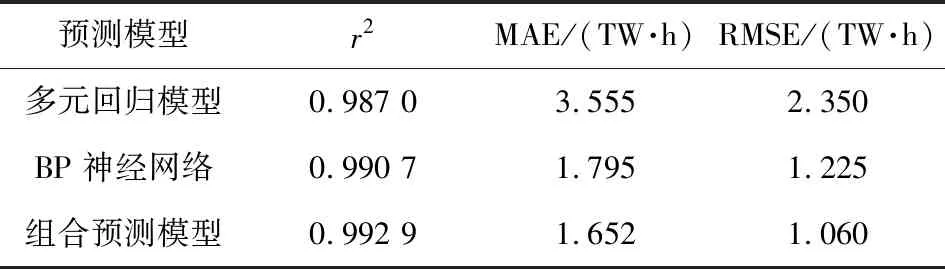
表12 不同模型的决定系数对比
由表12可见,组合预测模型的决定系数最大,平均绝对误差和均方误差最小,其预测效果最好。
3 结 语
结合经典的多元线性回归模型和BP神经网络模型对中国年度用电量进行了组合预测。在利用多元线性回归模型时,对于存在的共线性现象进行了检测和纠正,最终的组合预测能够吸收并结合2种模型的优点。线性回归模型的局限性是模型的线性方法决定其无法描述复杂的非线性因素对发电量的影响情况,而神经网络技术则较好地考虑非线性因素的影响情况,较好地弥补这一缺点,同时将历史负荷的发展规律和较高的预测精度相结合,提高了预测的准确性和精确度。
