函数思想在高中数学解题教学中的应用策略
2023-11-26张丽英
张丽英
【摘要】在新课改背景下,将函数思想融入高中数学解题教学中,有助于学生核心素养的发展及解题教学质量的提升.就目前情况来看,部分学生在参与解题训练的过程中仍存在盲目解题、难以理清题目线索、解题效率较低等问题.为突破现状,文章从函数思想的具体内涵以及其在高中数学解题教学中的应用价值出发,探究如何在不等式问题、几何问题、方程问题、数列问题等题型练习中应用函数思想,以期帮助学生养成运用函数思想解题的习惯,提高解题效率.
【关键词】函数思想;高中数学;解题教学
在高中阶段,解题教学是数学课程中的重点内容,但部分学生在解题中缺乏对知识内容的整体认识,解题思维存在一定的局限性,因而导致其数学成績始终无法得到提升.高中数学中包含了诸多思想,函数思想是其中的一种重要解题思想,帮助学生形成良好的函数思想有利于其形成一题多解、举一反三的解题能力.因此,教师应充分关注函数思想的重要价值,将其运用于实际的解题教学中,突破传统题海战术的桎梏,助力学生全面发展.
一、函数思想的具体内涵
函数的本质就是变化与对应,在变化与动态中,找寻两个量之间始终不变的对应关系.在高中阶段的数学学习中,不等式、几何、方程、数列等均属于静态的,用常规的思想难以准确描述其本质特征,而函数思想能顺利解决这一问题,以动态的方式对内容作出诠释,建立函数关系或构造函数,使问题得以解决.
二、函数思想在高中数学解题教学中的应用价值
函数思想主要体现了处于变化中的量和量之间的关系,帮助学生养成运用函数思想解决数学问题的习惯具有以下价值:第一,在解题教学中,培养学生运用函数思想解题的习惯,有助于学生深化对函数的本质认识,构建完善的知识体系,强化自身学习理解能力.第二,引导学生采用函数思想解决数学问题,可突破常规解题教学以教师为主导的现状,充分凸显学生的主体地位,帮助学生形成自主解题的良好习惯,并能使学生在函数思想的引领下掌握科学的解题方法,逐渐提高自身解题效率.第三,学生掌握了函数思想解题的基本步骤,就可以掌握复杂的数学知识,让函数成为串联各知识点的主线,从而在循序渐进中领悟数学知识的内在联系,提高自身核心素养.
由此可见,在高中数学解题教学中应用函数思想,有助于发展学生思维能力及提升课堂教学质量.因此,在实践中,教师需要深刻把握函数思想的具体内涵,基于学生的思维能力合理设计、安排教学内容,营造良好的学习氛围,帮助学生实现全面发展.
三、函数思想在高中数学解题教学中的应用策略
(一)不等式解题中函数思想的应用
不等式是高中数学中的基础内容,通过建立函数思想模型结合数形图像能快捷地解决此类问题.在指导过程中,教师可以引导学生基于函数思想,利用分布区间获得数据,将不等式转化为便于思考、理解的函数形式,从而规避在常规计算中容易出现的问题.
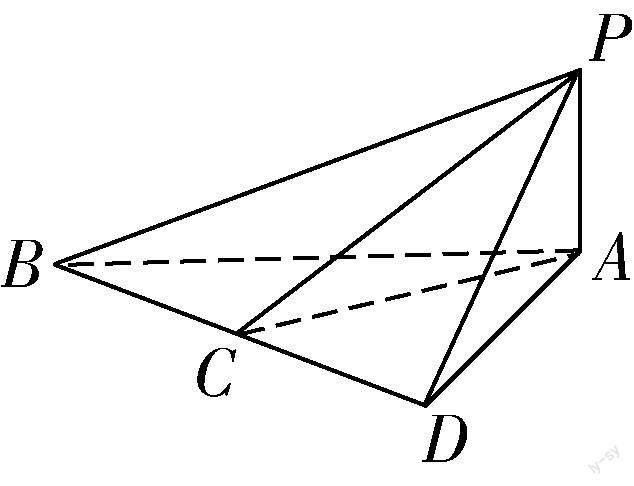
以人教版必修第一册“基本不等式”为例,学生在本课学习中需通过具体实例理解不等式,并在梳理等式性质的基础上,以类比的方式探究不等式性质,解决相关不等式问题.结合重点内容,教师可为学生设计这样一道题目:设a>b>c,且a+b+c=0,抛物线y=ax2+2bx+c被x轴截得的弦长为l,求证:3 思路分析 首先,根据题意可以发现弦长l是与a,b,c相关的变量,能够建立l=f(a,b,c)的表达式,从而确定该函数的值域,而为明确l=f(a,b,c)的值域,则需解决“1.求变量l关于a,b,c的解析式.2.将多元函数通过集中变量、消元或变量代换转化为一元函数.3.确定一元函数的定义域.”这三个问题. 从上述解题过程不难看出,运用函数思想解决不等式问题,能极大地提高解题效率,通过相互转化可顺利地完成解题.在此基础上,为帮助学生发展思维能力,掌握函数思想在不等式问题中的解题方法,教师还可以设计举一反三的延伸问题,引导学生利用构造函数的方式解决:“当x∈(1,2)时,不等式x2+mx+4<0恒成立,求m的取值范围”这一变式问题,提高学生举一反三的能力. 如上,运用函数思想解决不等式问题,可以帮助学生进一步体会利用函数观点统一方程及不等式的数学思想方法,使其掌握解决问题的基本技巧,在训练中加以运用,最终提高知识解题能力. (二)几何解题中函数思想的应用 几何问题是高中阶段数学的核心内容,复杂的立体几何等内容在高考中分值占比较大,运用函数思想能顺利解决此类问题,提升解题质量.因此,在教学中教师应合理引导学生基于函数思想处理几何问题. 以人教版高一必修第二册“立体几何初步”为例,基于重点内容,教师可为学生提供相关练习,引导学生掌握函数思想在不同几何问题中的应用方法:如图所示,已知PA⊥平面ABC,AD⊥BC于点D,BC=CD=AD=1. (1)令PD=x,∠BPC=θ,将tanθ表示为x的函数,并求其最大值; (2)在直线PA上是否存在一点Q,使得∠BQC>∠BAC成立. 思路分析 (1)为寻求tanθ与x的关系,可以将θ转化为∠PCD-∠PBD. 如上,将立体几何与代数融合起来可帮助学生运用函数思想快速解决此类问题,在后续练习中,教师还需要勤加指导,注意培养学生的耐心和专注力,使学生逐渐掌握解题方法. (三)方程解题中函数思想的应用

方程由一个未知数或多个未知数的等式组成,方程与函数之间具有密切联系,通过简单的转化可以使学生运用函数思想,抓住数与式的特点,使问题得以解决.在解题教学中,教师需要引导学生勤加练习,提高自身学习能力,结合函数与方程之间的内在联系完成解答.
如上,在讲解方程问题的过程中,教师可以通过函数思想的渗透,引导学生掌握科学的解决问题的方法,从而帮助学生在训练中深化对方程的根与函数零点关系的理解以及利用函数图像确定零点个数的基本方法,提高学生思维能力,把握数学知识之间存在的联系.
(四)数列解题中函数思想的应用
从近年来高考试卷的内容不难发现,数列版块逐渐扩增,对学生解题思维提出了更高的要求.然而,部分学生在解决数列问题的过程中,通常会采用常规的计算方法,此种方式既耗费精力,还可能出现计算失误.基于这一情况,在讲解数列相关问题的过程中,教师可以引导学生将其视为一种特殊的函数,从而降低数列知识的难度,顺利求解.
如上,在解决数列问题的过程中应用函数思想,能帮助学生减轻计算负担,切实提高其解题效率.除此之外,考虑到部分学生较为粗心,在完成解题后,教师还可以引导学生进行验算,以逆向推理的方式整理正确答案.
结 语
综上所述,在高中数学解题教学中,教师应通过函数思想的渗透,为学生讲解便捷性解题技巧的使用方法,帮助学生在训练中感受函数思想解题的优势,逐渐掌握函数思想解决数学问题的诀窍,积累丰富的解题经验,巧用函数思想,开启数学解题之门.相信在广大教师的共同努力下,高中数学解题教学质量将得到显著提升.
【参考文献】
[1]杜勇飞.高中数学解题中学生反思能力的培养方法研究[J].数理化解题研究,2022(36):38-40.
[2]李娟.新高考背景下高中数学解题教学的策略[J].新世纪智能,2022(A0):64-65.
[3]陈林.数学思想方法在高中数学解题中的应用[J].数学之友,2022(24):61-63.
[4]卓柳珊.函数图像在高中数学解题中的应用[J].中学教学参考,2022(08):32-34.
[5]陈笃因.优化高中數学解题思维方法的有效策略[J].中学课程辅导,2022(05):81-83.
