基于支持向量机的西安城市要素影响地表温度研究
2023-11-26李明哲周庆杨艳
李明哲, 周庆, 杨艳
(天津城建大学建筑学院)
1 引言
城市热岛是由于城市化,人口密集的城市区域的空气温度或地表温度明显高于周围郊区的现象。近年来城市由于热岛效应正在逐渐变暖,分析地表温度变化的影响因素有助于缓解城市热量积累[1]。
陈友军分析了PD、AI、LPI和CONTAG 等景观格局指数与LST 的相关关系,认为存在一定的线性关系[2]。Estoque RC 定量分析了不透水面和绿色空间与地表温度的关系,认为较低的不透水面密度和较高的植被是缓解热岛效应的有效手段[3]。
本文对比线性回归和支持向量机两种算法,对城市要素指标进行统计分析,得到城市要素影响地表温度的重要性排序,并解释影响地表温度变化。
2 研究区概况
西安市地处关中平原中部,是陕西省省会城市。本研究区选择主城区中心长宽均为10km的区域,坐标为东经107°40'~109°49',北纬 33°39'~34°45'。
3 材料与研究方法
3.1 数据来源
地表温度反演所用Landsat 8数据来自地理空间数据云。数据预处理包括投影转换、几何校正、辐射校正和图像切割等。建筑矢量数据和POI等数据来自乔峰地球下载。土地分类数据采用哨兵2号影像(sentinel-2),采用建筑矢量数据辅助,阈值条件分类方法进行土地分类。
3.2 指标选择
本研究共选取6项常见的影响地表温度的城市要素指标[4-6]。归一化植被指数(NDVI),改进的归一化差异水体指数(MNDWI),建筑密度(BD),植被密度(VD),人口密度(PD),感兴趣点(POI)。
3.3 研究方法
3.3.1 地表温度反演
本文采用辐射传输方程法反演地表温度,原理是将卫星观测到的热辐射总量中减去大气影响的地表热辐射量,得到地表热辐射强度,最后转化为地表温度。采用Sobrino提出的NDVI阈值法计算地表比辐射率,普朗克公式求LST(摄氏度的地表温度)。
3.3.2 支持向量机算法
支持向量机方法是由Corters 和Vapnik 在1995年提出并正式发表的一种借助凸优化技术求解的智能优化方法,主要用于分类与回归,是建立在VC 维理论和结构风险最小化原理基础上的机器学习方法,具有参数少、样本小、泛化能力强和理论全局最优解唯一等特点。
4 结果与分析
4.1 城市要素与地表温度指标相关性
地表温度样本数据(LST)主要集中在31℃至38℃,呈正态分布。LST与BD、MNDWI和POI相关性为三颗*,显著正相关,相关系数分别为0.54、0.26和;LST与PD相关性为两颗*,正相关,系数为0.15;LST 与VD和NDVI相关性为三颗*,显著负相关,相关系数分别为-0.49 和-0.51。BD、VD、MNDWI、NDVI、PD和POI相关性矩阵中,VD和NDVI的相关性最高,正相关系数为0.9,其次是MNDWI和NDVI,相关系数为-0.80。
4.2 模型评价
本研究对线性回归、支持向量机、梯度提升和随机森林四个模型交叉验证以训练和验证准确性。此方法将 80% 的数据划分为训练集,其余 20% 为测试集。后在此看不见的测试集(称为out-of-bag)上测试由训练产生的模型,以获得模型准确度的估计,重复100 次,并报告准确度的分布(R2和RMSE),确保模型不会过度拟合数据。在使用统计模型时避免过度拟合必不可少,但大多现有研究都忽略了这一点。交叉验证通过在看不见的数据上评估模型来帮助避免这种情况。
R2越大越好,RMSE 越小越好。线性回归算法的R2为0.42,RMSE为0.96;支持向量机的R2为0.46,比线性回归大0.04;RMSE为0.91,比线性回归小0.05。可见,支持向量机在评价城市要素对地表温度重要性影响方面更有优势。
4.3 城市要素影响地表温度重要性
使用变量重要性分析计算50 个置换和RMSE损失函数的变量重要性度量的平均值。使用set.seed函数使排列的随机选择过程可重复。
由图1 可知,城市形态指标中对地表温度影响的重要性排序分别是NDVI、BD、MNDWI、PD、VD和POI。线性回归算法中,各个城市形态指标对地表温度的影响差异较大,NDVI的影响最大,远远大于BD和MNDWI,VD和POI的影响接近0。但支持向量机算法中,各城市形态指标对地表温度的影响差异较小。支持向量机的RMSE 均值明显比线性回归要小,说明支持向量机在对地表温度影响重要性方面优于线性回归算法。
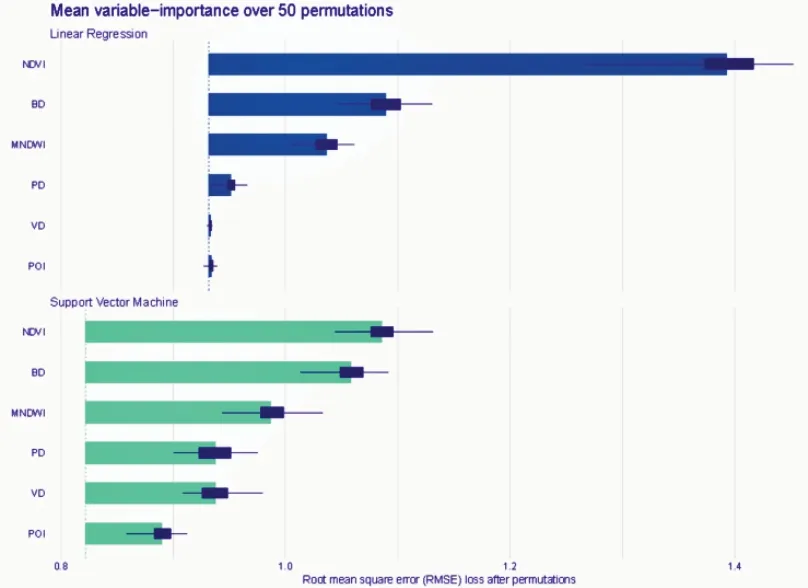
图1 变量重要性分析
4.4 局部变量相关分析
4.4.1 各机器学习算法偏相关图对比
BD值的范围在0至0.55之间,线性回归和支持向量机算法中,BD与LST均呈正相关关系,整体趋势也比较一致。MNDWI、NDVI与LST呈负相关关系,线性回归算法斜率较大。PD、POI和VD与LST呈轻微负相关关系(见图2)。

图2 线性回归和支持向量机偏相关图
采用支持向量机对各个指标再次进行回归分析,发现VD对LST的影响更加清晰,随着VD值增加,LST值逐渐下降,当VD值在0.7 左右时LST达到最小值,之后LST逐渐升高。LST随着MNDWI增大,先升后降,当MNDWI在-0.2 时,LST达到最小值34.05。
4.4.2 偏相关图
由图3可知,80%的BD样本值集中在0.12至0.4之间,LST集中在33.8℃至35.2℃随着BD 增大呈上升趋势。80%的MNDWI样本值集中在-0.3 至0.21之间,LST集中在34.25℃至34.45℃随着MNDWI增大呈下降趋势,当MNDWI在-0.18 时,LST 最小,之后略有上升。90%的VD样本值集中在0 至0.62 之间,LST集中在33.95℃至34.65℃随着VD 增大呈下降趋势;当VD在0.7 时最小,之后逐渐上升。PD样本值均匀分布在0 至210 之间,LST集中在34.2℃至34.6℃,随着VD增大LST整体呈波动缓慢下降,当PD值在120 左右时,LST急剧下降。POI样本值集中在0至440之间,LST集中在34.3℃至34.7℃,随着POI增大LST先急剧下降;当POI值在350 左右时,LST最小,后急剧上升;当POI值在800 左右时,LST达到最大值34.52℃。

图3 线性回归与支持向量机单变量偏相关图
5 讨论
以往研究多采用线性回归算法,只描述线性变化趋势。支持向量机算法,在描述城市形态指标对地表温度的整体和局部影响均表现良好,精度较高。但本文未探究不同尺度对支持向量机算法的影响,在城市热环境季节性,及城市要素指标选取方面也还有局限性,有待进行更全面深入的研究。
6 结语
城市要素与其地表温度之间的联系不可否认,通过机器学习算法中的支持向量机进行变量重要性和局部变量相关性分析,可得到重要性排序同时可预测城市地表温度。①支持向量机算法在评价城市要素对地表温度影响重要性程度上,准确率高,能发现更多的细节。②建筑密度、植被密度、人口密度、改进归一化水体指数、归一化植被指数和感兴趣点六个城市要素指标中,归一化植被指数影响最大,其次是建筑密度,感兴趣点最少。③影响较大的归一化植被指数和建筑密度,其影响趋势不是简单的线性关系,呈现非线性增长或降低,变化速率也非均匀的。④通过双变量分析,BD、VD和LST存在一定相关关系,且非线性关系,城市形态指标之间存在相互影响机制。
