木核心钢管混凝土短柱轴压性能试验研究

2023-11-25乔玲玲阿里甫江夏木西李成祥刘祥祖周珠珠穆合普力库尔班

结构工程师 2023年5期

乔玲玲阿里甫江·夏木西李成祥刘祥祖周珠珠穆合普力·库尔班

（新疆大学建筑工程学院，新疆乌鲁木齐 830047）

0 引言

钢管混凝土结构（Concrete-Filled Steel Tube，简称CFST）自19世纪80年代被用作英国赛文铁路桥的桥墩开始，经历了漫长的发展与应用史，并已被证实具有良好的抗震性能、强度和能量吸收及变形能力，并作为竖向承重构件广泛应用在高层建筑、大跨度桥梁以及海岸工程等承受巨大荷载的结构中，现已成为常规的工程结构构件［1-2］。然而，在钢管混凝土中主要承受压力的混凝土占结构总体自重最大，这对结构力学性能有很大影响且大规模生产混凝土势必造成耗能增加，不环保。

为弥补钢管混凝土的自重、环保缺陷以及木结构的材料、力学劣势，有学者提出木核心钢管混凝土（Timber Core Concrete-Filled Steel Tube，简称T-CFST），也即借助木材吸湿膨胀后与混凝土的粘结、夹持摩擦力［3］，用木核心代替一部分核心混凝土的同时，外钢管和外包混凝土为木核心提供了保护机制，以一种新型组合结构的方式共同承受荷载。

Karampour等［4］和Ghanbari等［5］先后对纯木填充的钢管进行了研究，结果表明，木材阻止了钢管的局部屈曲，短柱的破坏发生在木材上，长柱的破坏发生在钢材上，填充木材具有可行性。Nabati等［6］研究了用CFRP材料加固的T-CFST的轴压表现，发现木材的使用对结构效率的提高十分显著，CFRP可以延迟组合结构的局部屈曲且提高了结构的轴向延性；Azandariani等［7］使用有限元研究木核心钢管混凝土在压缩下的非线性非弹性响应，还通过理论分析以验证数值结果，研究表明木材可以全部或部分代替混凝土，不仅减轻了自重，还有不错的能量吸收能力。

然而，现阶段对T-CFST的研究集中在国外，在国内此类研究鲜见报道，但是随着人们对轻钢结构与高效率承重结构的追求，未来在建筑中使用T-CFST具有一定的前景。因此，有必要对其进行受力性能的研究，旨在扩充目前国内相关领域的空缺。基于该领域研究现状，本研究以核心材料为主要变化参数，比较了轴心受压下CFST、空心钢管混凝土（Hollow Concrete-Filled Steel Tube，简称H-CFST）、空心配筋钢管混凝土（Hollow Reinforced Concrete-Filled Steel Tube，简称HRCFST）、空心夹层钢管混凝土（Hollow Doubleskin Concrete-Filled Steel Tube，简称HD-CSFT）和圆木或方木核心的T-CFST和配筋的T-CFST（Timber Core Reinforced Concrete-filled Steel Tube，简称T-RCFST）等8种组合类型的钢管混凝土衍生结构。

1 试验概况

1.1 试件设计

设计了CFST（代号为CF）、H-CFST（代号为H-CF）、H-RCFST（代号为H-RCF）、HD-CSFT（代号为HD-CF）和圆木或方木核心的T-CFST（代号为YT-CF和FT-CF）和配筋方木或圆木核心的TRCFST（代号为YT-RCF和FT-RCF）等8种试件，并对应每一组准备2根重复试件，总共制备16根圆形截面试件。依据我国《钢管混凝土结构技术规范GB 50936—2014》（简称《CFST规范》）［8］和材料市场供应情况确定试件尺寸：直径为D=165 mm，长度为H=500 mm，空心直径dh=70 mm，则长径比为3.03，属于短柱试件。钢管选用Q355B钢，壁厚t=3 mm；纵筋采用HRB400带肋钢筋，直径为8 mm，数量为6；箍筋采用CRB550冷轧钢筋、直径dl=4 mm，环径dr=120 mm，间距s=50 mm；木核心采用无明显缺陷的新疆杨木，圆形木核心截面直径取dtim=70 mm，方形木核心截面边长为btim=70 mm。T-RCFST试件构造和详细参数如图1所示。

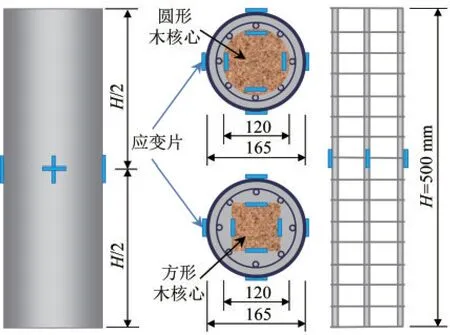
图1 T-RCFST构造示意图Fig.1 Illustration for formation of T-RCFST specimen

1.2 材性试验

按照《金属材料拉伸试验第1部分：室温试验方法》（GB/T 228.1—2010）［9］进行拉伸试验。测得钢管屈服强度fys=377.06 MPa、弹性模量Es=212 655 MPa，纵筋屈强度fyb=437.35 MPa，应力-应变曲线如图2所示。

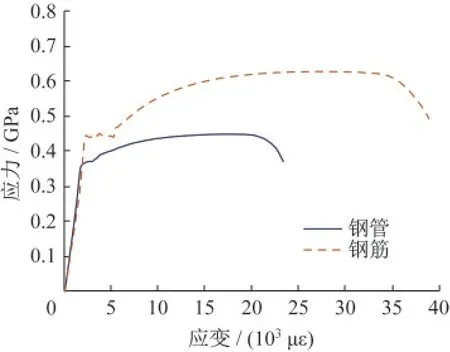
图2 钢管和钢筋的材性拉伸实验Fig.2 Material tensile tests of steel and reinforcement

普通混凝土的试配强度为C45，28天立方体抗压强度fcu=45.5 MPa，规范推算得到混凝土轴心抗压强度fc=29.9 MPa。

根据《木材含水率测定方法》（GB/T 1931—2009）［10］，从原材料取样制作30个尺寸为20 mm×20 mm×20 mm的试样。通过标准试验过程，得到该试验新疆杨木含水率为5.78%。按照《木材顺纹抗压强度试验方法》（GB/T 1935—2009）［11］，先从原材料取样制作30个30 mm×20 mm×20 mm的试样。当荷载下降至极限荷载的70%时终止加载，得出木材顺纹抗压强度为42.63 MPa。将计算结果换算成含水率为12%时的顺纹抗压强度，根据规范公式换算得到含水率为12%时的顺纹抗压强度ftim=29.35 MPa。

1.3 加载方案及测点布置

在钢管高度等分的位置分别绕周长等距设置4个横向应变片，相应与横向应变片垂直的方向设置一个竖向应变片，每根钢管共计8个应变片，钢筋仅粘贴纵向应变片，每隔一根钢筋粘贴1个（见图1）。试验在YJW10000微机控制液压伺服压力机上进行，采用位移加载，速度控制为3 mm/min，实心试件极限位移控制为35 mm，空心试件极限位移控制为25 mm，预加载量控制为50 kN。图3为试验加载照片。

图3 试件加载图Fig.3 Photograph of loading of specimen

2 试验结果及分析

2.1 破坏模式

试件的内外破坏形态如图4所示。可以看出，试件整体破坏模式均以钢管发生局部失稳为特征，其中CFST和HD-CFST试件的破坏模式相似，为剪切破坏模式；与CFST和HD-CFST不同，空心试件和木核心试件因端部有孔洞和木核心无法有效约束混凝土向试件中心脱落和破坏，造成端部钢管提早鼓起变形，表现出明显的膨胀和褶皱破坏特征。为了进一步观察内部混凝土的破坏形态，将钢管剖开。CFST和HDCFST试件的内部混凝土在钢管剪切滑移处呈现与钢管一致的剪切破坏，但是与CFST试件相比，HD-CFST试件由于双层钢管的双向约束作用，内部混凝土没有失去整体性，而CFST试件的混凝土已经完全剪切分离成两部分；H-CFST试件的混凝土由于缺少核心部分的约束，组织疏松，受压后产生通缝，被剖成两块。相比之下，在混凝土内配筋的H-RCFST的内部混凝土比较完整，没有过多破坏，这与配筋提高了试件的整体性有关；配置木核心的YT-CFST和FTCFST，虽保持了大体的完整，但端部较为脆弱，呈现与外钢管一致的剪切破坏，这可能与木材抗剪强度较低有关；由图4（f）和图4（h）可以看出，在木核心的基础上配置钢筋有助于提高试件的横向抗剪性能，使试件仅在外钢管剪切处出现磨损，这可能是因纵筋提供的抗剪强度，阻止混凝土横向变形，从而防止木核心横向破坏。

图4 试件内外破坏形态照片Fig.4 Photograph of internal and external failure patterns of specimens

2.2 受力性能

2.2.1 荷载位移响应

所有试件的荷载-位移曲线如图5所示。

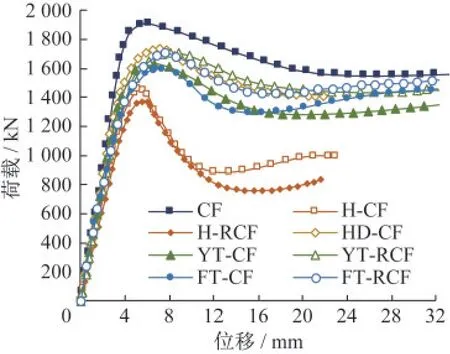
图5 荷载-位移曲线Fig.5 Load-displacement curves

弹性工作阶段：H-RCFST的弹性刚度最小，YT-CFST、YT-RCFST、FT-CFST和FT-RCFST的弹性刚度与CFST相差不大，这表明新疆杨木等体积替换核心混凝土后，并不会明显降低钢管混凝土构件弹性范围内的工作性能。

弹塑性工作阶段：各类试件的工作性能开始产生明显差异。CFST所受荷载值的增长速度最快，增长幅度也最大，H-RCFST所受荷载的增长速度最慢，且很快达到峰值荷载，说明混凝土用量越多，试件弹塑性阶段受力性能越好；当混凝土用量减小时，与其他试件相比，YT-RCFST、FTRCFST和HD-CFST在弹塑性阶段荷载值的提升较为显著，三者的峰值荷载近似相等，但T-RCFST的峰值位移大于HD-CFST的峰值位移，说明，与HD-CFST相比，T-RCFST具有更优的弹塑性变形能力，其弹塑性受力性能优于HD-CFST；与YTCFST和FT-CFST相比，对应的YT-RCFST和FTRCFST的峰值荷载峰值位移更大，表明钢筋可有效提升T-CFST的弹塑性工作能力。

峰值荷载后试件进入塑性变形阶段：CFST峰值荷载后的受力性能呈现下降缓慢的趋势，而HCFST和H-RCFST峰值荷载后受力性能呈现迅速下降的趋势，说明当仅减少混凝土用量时，配筋不能改善H-CFST脆性大的问题，且与H-CFST相比，H-RCFST在峰值荷载后受力性能下降更显著，说明仅加配纵筋不能改善H-CFST塑性阶段的受力性能，相比之下HD-CFST在峰值荷载后依旧保持良好的塑性变形能力，表明相较于配钢筋的方法，在核心区加配钢管可以有效改善空心钢管混凝土脆性明显的特点；与FT-CFST相比，FTRCFST下降段更加平稳，表明FT-RCFST的塑性变性能力优于FT-CFST，这一点在YT-CFST和YTRCFST的对比分析中也有体现；与其它各类试件相比，YT-RCFST峰值荷载后受力性能下降趋势最缓慢，这表明YT-RCFST的塑性变形能力相对最优。

综上所述，与HD-CFST试件相比，木核心配筋钢管混凝土试件的变形能力更优；配筋虽然不能改善H-CFST试件的脆性特征，但可有效改善YT-CFST和FT-CFST的受力性能。

2.2.2 钢管的荷载应变响应

钢管的荷载-应变曲线如图6所示。在达到峰值荷载前，各类试件的钢管纵向应变发展明显快于横向应变的发展。H-RCFST试件的纵向应变最小，说明内部混凝土缺少核心部分时，配筋不仅无法提高试件承载力，还会减小其变形能力；配筋后的YT-RCFST和FT-RCFST的纵向和横向应变均大于未配筋的YT-CFST和FT-CFST，说明由于钢筋笼对核心木和混凝土的套箍作用延缓了核心混凝土的膨胀，也同时防止了混凝土的压碎。

图6 钢管的荷载-应变曲线Fig.6 Load-strain curves of steel tube

2.2.3 木核心的荷载应变响应

通过木核心纵向中心位置粘贴的横向和纵向应变片的数据，绘制出荷载与木核心的纵向和横向应变关系曲线，如图7所示。可以发现，与方形木核心试件相比，圆形木核心试件配筋后的纵向和横向应变的提升效果更好且荷载应变曲线更加光滑，说明配置钢筋与圆形木核心钢管混凝土更能发挥其性能，核心混凝土与钢筋笼对圆形木核心的约束，进一步改善圆形木核心的变形性能。

图7 木核心的荷载-应变曲线Fig.7 Load-strain curves of timber core

2.3 关键力学指标

2.3.1 峰值荷载

各试件的峰值荷载值如表1所示，其分布柱状图如图8所示。CFST的峰值荷载最大（即1 911.4 kN），H-RCFST的峰值荷载最小（即1 374.1 kN），这说明混凝土的用量显著影响试件极限承载能力的大小，且与H-RCFST试件相比，H-CFST的峰值荷载更大，这说明配筋不能有效改善空心钢管混凝土构件的承载力，但HD-CFST的峰值荷载又远高于H-CFST，这说明与配纵向钢筋相比，在核心区加配钢管用于改善空心钢管混凝土受力性能的方法更有效；和H-CFST不同的是，与YT-CFST试件相比，YT-RCFST试件的峰值荷载更大，这表明配筋明显改善了YT-CFST试件的承载力，这一点在FT-CFST中也有所体现；与FTCFST的峰值荷载相比，YT-CFST的峰值荷载更大，但加配纵筋后，FT-CFST的峰值荷载与YTCFST试件的峰值荷载基本相同，这表明仅加配木核心时，圆形木核心受到外包钢管和混凝土的约束效应优于方形木核心，但再加配纵向钢筋后，虽然二者的承载力均有提升，但纵向钢筋对FTCFST试件承载能力的提升效果更明显。

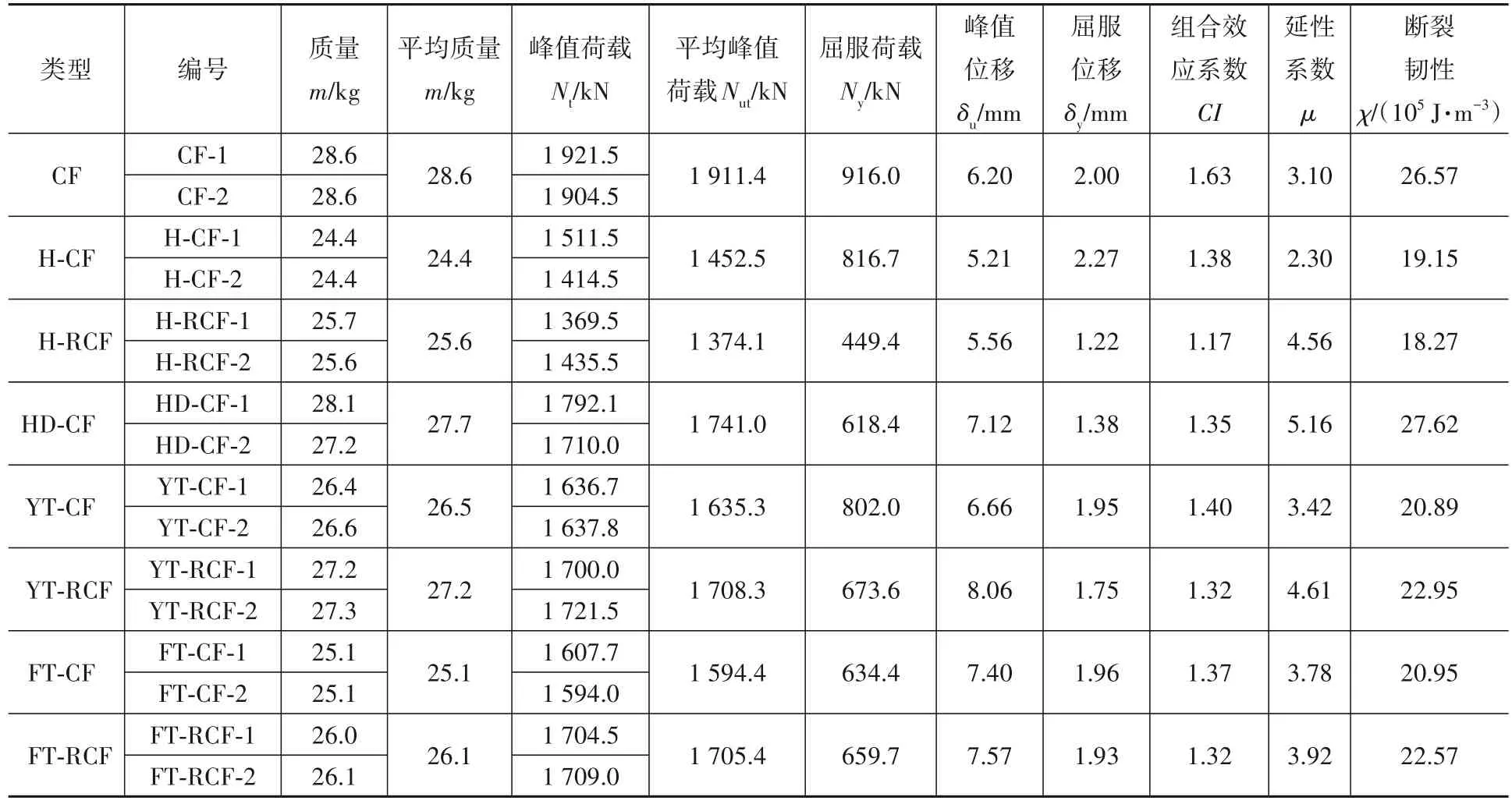
表1 试验结果Table 1 Test results

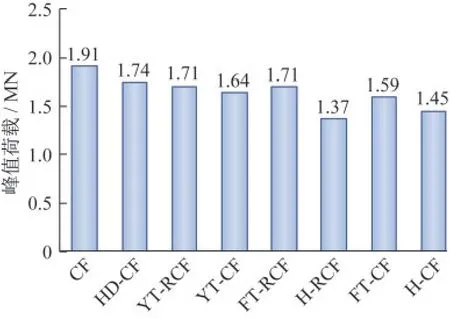
图8 峰值荷载Fig.8 Peak load

试验时对各试件进行了测重，各试件的质量如表1所示，图9为各类试件单位质量的最大承载力。CFST的单位质量最大承载力最高（即66.8 kN/kg），YT-RCFST的单位质量最大承载力次之（即62.9 kN/kg），H-RCFST的单位质量最大承载力最低（即53.5 kN/kg）。由于YT-RCFST的单位质量最大承载力与CFST的单位质量最大承载力相差不大，但远高于H-RCFST试件。因此，在H-RCFST中加配圆形木核心组成YT-RCFST的做法是合理有效的。由于YT-CFST的质量轻于FTCFST，因此与FT-CFST相比，YT-CFST的单位质量最大承载力更大，说明YT-CFST的工作性能更优，这与YT-RCFST和FT-RCFST对比特点相一致；与YT-CFST相比，YT-RCFST的单位质量承载力略有提升，说明纵筋提高试件承载能力的优势大于自重增加的劣势，这与FT-CFST和FT-RCFST的对比结论相一致。

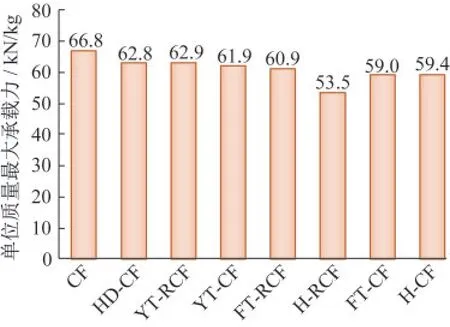
图9 单位质量最大承载力Fig.9 Load-bearing capacity per unit mass

2.3.2 断裂韧性

评价材料抵抗或者延缓裂纹持续扩展和抵抗脆性破坏的能力可用断裂韧性来衡量。可通过单位体积所吸收的能量来表达：

式中：N、δ分别为各点荷载和位移；δf为极限位移；D和H分别为试件直径和高度。

取钢管材料试验极限抗拉强度对应的位移16 mm为极限位移，在图5所示的荷载-位移关系曲线上进行数值积分，得出各试件相应的断裂韧性值，如表1和图10所示。通过对比发现，配置圆或方木核心的钢管混凝土试件断裂韧性均小于CFST和HD-CFST试件，说明用新疆杨木替代部分核心混凝土虽然减轻了试件自重但会降低试件的能量吸收能力；分别对比YT-CFST、FT-CFST和YT-RCFST、FT-RCFST发现配置纵筋分别对YTRCFST和FT-RCFST的韧性提高了8.97%和7.14%，表明在木核心钢管混凝土试件内配置纵筋不仅可以提高试件的承载力，同时提高韧性。对比H-CFST与H-RCFST发现，在空心钢管混凝土内配置纵筋并不能给试件在性能上带来积极影响，反而降低其能量吸收能力，因而在H-CFST内配置纵筋不是很有效。因此，木核心钢管混凝土的优势在此体现出来。相对于其它试件，HDCFST的断裂韧性最大，但其在减轻混凝土质量和材料用量方面作用并不明显。与FT-CFST相比，YT-CFST的韧性没有差别，说明木核心截面形式对构件能量吸收能力的影响不大。因此，采用木核心代替部分混凝土的方式可以一定程度上减轻构件自重，且能降低因混凝土用量减少带来的构件断裂韧性的损失。

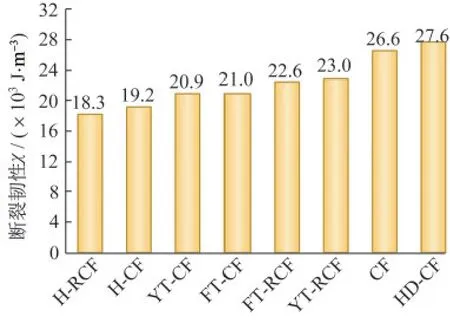
图10 断裂韧性Fig.10 Fracture toughness

2.3.3 延性性能

材料在受到最大荷载到破坏前的塑性变形能力可用延性系数来衡量，其量化表达式为

式中：δu为峰值荷载Nut时的位移；δy为屈服荷载Ny时的位移。

式（2）中如何确定δy是关键，确定过程如下：根据图6，钢管处于平面应力状态。此时，将钢管在拉伸试验中的屈服应变作为整体受力时钢管的屈服应变是有偏差的。

根据图11所示的平面应力状态，假设钢管在屈服之前处于弹性阶段，屈服前满足：

图11 钢管实际应力状态Fig.11 Real stress condition of steel tube

式中：εsv和εsh为通过应变片测得的钢管测点处在某时刻的应变；Es为钢管实际弹性模量，由前期拉伸试验得到；σsv和σsh分别为与εsv和εsh所对应的纵向和横向应力。

根据平面弹性应力-应变方程得到：

根据Von Mises屈服准则有：

式中，fsy即为该数据点处的实际应力，将式（3）代入式（4），可得：

式中，νs为泊松比，取νs=0.3；εsy为该点的实际应变。

将计算得到的实际屈服应变在图6中进行校核得到实际的屈服载荷Ny，再根据图5得出Ny对应的δy，也即实际屈服荷载对应的位移值。

将计算结果列于表1中，并绘出相应的延性系数分布图，如图12所示。可以看出，由于核心材料的缺失，H-CFST靠近内部混凝土接近于素混凝土状态，脆性明显大于实心、致密的CFST，而HD-CFST的延性最高是因为内钢管的存在使得空心混凝土被双向约束，试件整体塑性变形能力得到明显加强，以致优于实心的CFST；在H-CFST中配置钢筋后，试件由于核心材料缺失造成的脆性得到了一定的减小，说明钢筋笼提高了试件的整体性和变形能力，抑制了脆性破坏；YT-CFST和FT-CFST的延性系数均大于CFST，也即在CFST中用木核心取代部分核心混凝土后，延性得到了一定的提升，这是因为混凝土的脆性大于木材；YT-RCFST和FT-RCFST的延性系数大于YTCFST和FT-CFST同样也衬托了钢筋笼抑制脆性发展的作用。

图12 延性系数分布Fig.12 Distribution of ductility Index

对CFST、YT-CFST、YT-RCFST、FT-CFST、和FT-RCFST进行延性系数和质量双重考量，配置木核心的各试件均在一定程度上减轻了自重，其中YT-CFST的质量为CFST的92.8%，而延性提高了10.1%；YT-RCFST的质量为CFST的95.4%，延性提高了48.6%；同理，FT-CFST在质量仅为CFST的87.9%的基础上，延性提高了21.8%，FT-RCFST以91.2%的CFST的质量，延性比CFST高出26.5%，这说明用木核心取代部分混凝土不仅达到了减轻自重的目的，还提高了试件的延性，在木核心的前提下再配置钢筋，虽然增加了自重（YT-RCFST比YT-CFST重2.8%，FT-RCFST比FT-CFST重3.8%），然而延性也再次得到提升（YT-RCFST比YT-CFST延性提高了34.8%，FT-RCFST比FT-CFST延性也提高了3.9%，这也说明了圆形木核心与整体的组合效果更佳）。

2.3.4 组合效应

各试件峰值荷载Nut和名义强度No（No=Accfc+Assfys+Asbfyb+Atimftim）的分布柱状图如图13所示。不难看出：所有试件的Nut都远大于相应的No，说明钢管、混凝土、钢筋和木核心之间的相互作用产生了某种组合效应，使得试件整体性能显著提高，获得1+1＞2的效果。为了评估这种组合效应，引入组合效应指数CI进行评估，其表达式为

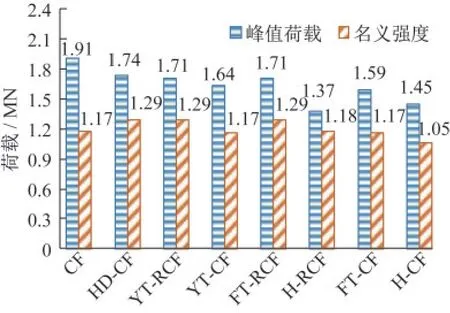
图13 峰值荷载和名义强度的关系Fig.13 Relationship of peak and nominal strength

式中：Acc、Ass、Asb和Atim分别为核心混凝土、钢管、钢筋和木核心的横截面面积；fc、fys、fyb、和ftim分别为核心混凝土、钢管、纵筋和木核心的强度。

计算得到的各试件CI结果如表1所示。可以看出，各试件CI值均大于1，说明无论是否加入木核心，各类试件都存在套箍效应，其对核心混凝土或是核心木都起到了一定的约束效果，使得试件的整体承载力明显大于各部分纵向名义强度的叠加。通过比较发现：H-CFST的峰值荷载NutH-CF与圆形木核心强度累加值之和为N1=NutH-CF+Ntim，Y=1 452.5+113=1 565.5 kN，与方形木核心强度累加值之和为N2=NutH-CF+Ntim，F=1452.5+143.8=1 596.3 kN，H-RCFST的峰值荷载NutH-RCF与圆形木核心强度累加值之和为N3=NutH-RCF+Ntim，Y=1 374.1+113=1 487.1 kN，与方形木核心强度累加值之和为N4=NutH-RCF+Ntim，F=1 374.1+143.8=1 517.9 kN，可见在H-RCFST中配置木核心能够显著提高试件的套箍效应，相较于H-RCFST与木核心强度累加值之和，YT-RCFST或FT-RCFST所产生的组合效应使得承载力分别提高了14.88%和12.35%，表明通过配置木核心的方式提高H-RCFST承载力是可行的；在HCFST中配置木核心同样能提高试件承载力，其中，YT-CFST所产生的组合效应使得承载力大于H-CFST与圆形木核心强度累加值之和，而FTCFST的组合效应未能使承载力超过H-CFST与方形木核心强度累加值之和，说明试件对圆形木核心的约束效应优于方形木核心，并且配置钢筋有助于提高木核心钢管混凝土试件的承载力。

2.4 承载力计算公式

我国《CFST规范》［8］给出基于统一理论HCFST短柱的轴压承载力计算公式，而我国《特殊铜管混凝土构件设计规程CECS 408：2015》（简称《R-CFST规程》）［12］通过在CFST强度的基础直接叠加纵筋名义强度给出R-CFST短柱轴压承载力计算公式。又根据上述实验结果，由于混凝土和木核心中产生的套箍效应，T-CFST的承载力高于H-CFST和木核心强度的叠加值。因此，仿照《RCFST规程》［12］的做法又结合本文实验结果，分别给出T-CFST和T-RCFST短柱的强度预估公式为

式中：

（1）NH-CFST为空心钢管混凝土短柱的承载力，《CFST规范》［8］给出的公式为

式中：Asc为钢管和混凝土横截面面积之和；fsc为HCFST横截面的组合强度；fc为混凝土轴心受压强度，对于空心构件fc均应乘以1.1；θ为空心构件的套箍系数，用式（9c）计算；B和C为截面形状对套箍效应的影响系数，对于空心截面可用式（9d）和式（9e）计算。

（2）Ntim为T-CFST和T-RCFST中，木核心的名义强度：

（3）Nro为H-RCFST和T-RCFST中，纵向钢筋的名义强度：

为验证本文推荐公式的可用性，对既有实验数据进行对比分析。为此，除了本实验，另收集不同套箍系数、木核心形状和木核心强度的共27组T-CFST实验数据。对比结果列于表2，实验值Nut和计算值NTF的比值Nut/NTF绘制于图14。

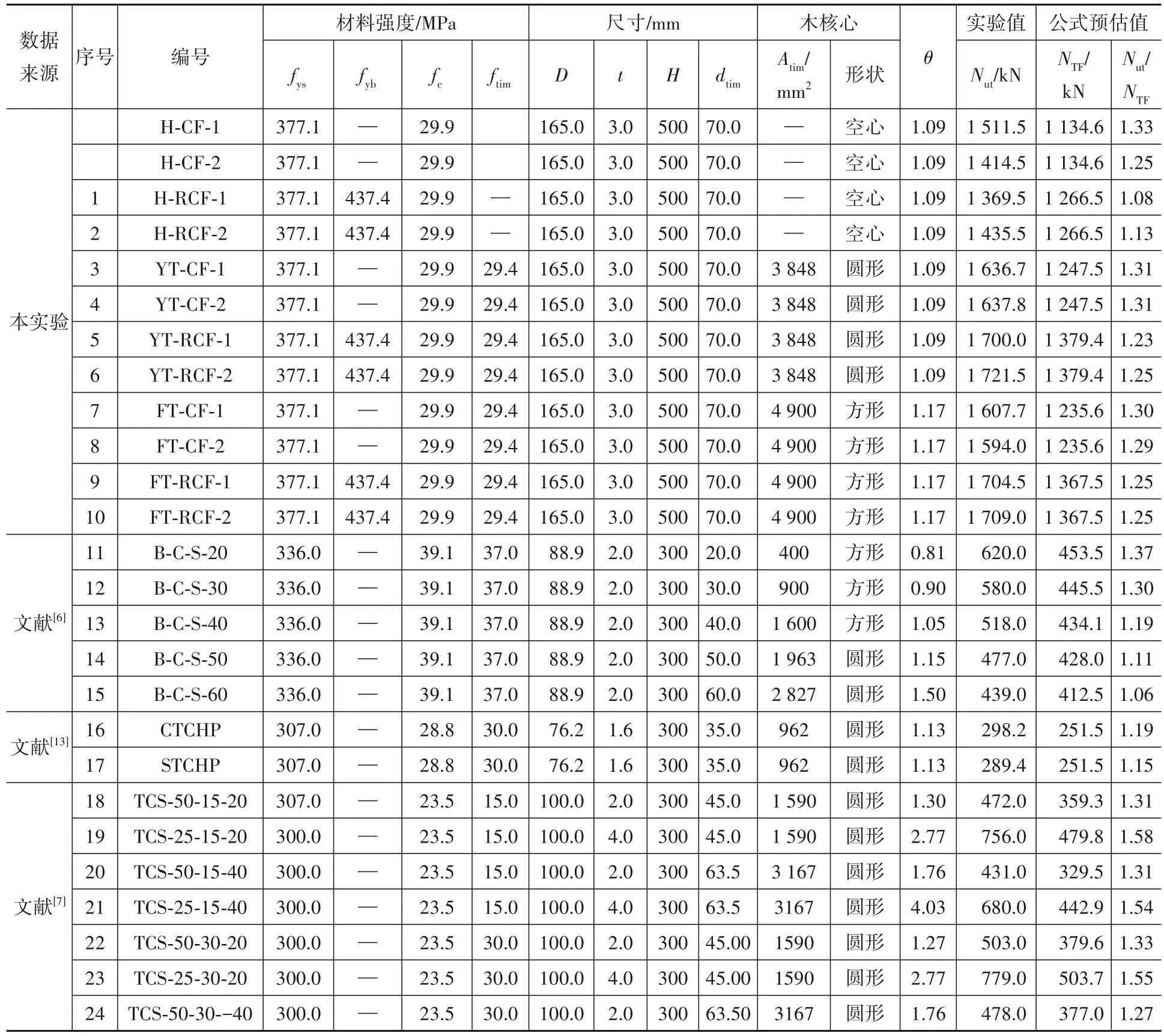
表2 实验值和计算值对比分析Table 2 Comparisons of experiment against prediction

图14 实验值和计算值对比分析Fig.14 Comparisons of experiment against prediction

经分析可知，空心钢管混凝土（H-CF）试件的规范计算Nut/NTF值的平均为1.29，偏保守；本文推荐公式预估的全部37根样本Nut/NTF值均大于1，说明公式预估结果均偏安全；推荐公式Nut/NTF值的平均值为1.29，说明公式预估结果的保守程度与规范空心构件计算公式一致；推荐公式Nut/NTF值的标准偏差为0.12，说明其预估结果离散型不大。可见，本文给出的计算公式可以用于圆形截面圆形和方形木核心钢管混凝土和配筋钢管混凝土短柱的轴压承载力，其结果是偏于保守的。