空间结构多维地震响应改进组合准则

2023-11-25曲扬陈刚程建军罗永峰

结构工程师 2023年5期

曲扬唐潮陈刚程建军罗永峰

（1.中建八局第三建设有限公司，南京 210046； 2.同济大学土木工程学院，上海 200092）

0 引言

空间结构在多维地震作用下，结构各振型和各方向上动力响应耦联效应显著［1］，现有的多维反应谱方法和多维推覆分析方法在获取各阶振型响应后，常采用传统CQC准则组合振型响应得到各方向的地震响应，然后采用SRSS准则将各方向响应组合得到结构总响应。然而，已有部分研究表明［2］，由于CQC准则理论基础中存在线弹性假定和高斯平稳随机过程假定，不适用于非线性结构，计算结果与试验结果偏差较大，且无法解释实际发生的部分震害现象。

采用SRSS准则组合得到结构多维总响应，在理论上易于理解，操作中便于实现。Wilson［3］基于主轴模型假定，推导出了不考虑各分量相关性的多维反应谱的SRSS组合公式。Smeby和Kiureghian［4］同样基于主轴模型假定，建立了多维反应谱法，认为当各分量沿主轴地震动强度相近时，各分量对应的地震响应相关性较低，可予以忽略。李英民等［5］通过引入三参数标定模型，研究了水平双向反应谱之间的相关规律，认为相关性与结构周期有关，不宜忽略，并给出了相关系数的统计回归公式和取值建议。Athanatopoulou等［6］对框架结构进行水平方向两维时程分析时发现，若直接按照主轴模型计算可能造成高达176%的误差。目前，虽已有部分研究成果揭示了SRSS组合准则的不合理性，但研究对象集中于框架结构，针对空间结构的相关研究仍然较少。

在实际地震动中，各分量输入之间必然存在一定的相关性，因此，SRSS准则的理论基础——主轴模型中地震动各分量互相独立、互不相关的假定与实际不符，空间结构的多维响应相关性尤为显著。Wang等［7］对大量关于组合准则研究文献的计算结果进行统计整理后发现，超过75%的研究成果表明，针对多维地震情形，采用SRSS准则将造成结构位移响应和单元力响应明显偏小，可见忽略多维地震响应相关性将显著低估结构的多维地震响应量；对于部分计算结果偏大的算例，是由于不同符号的响应经SRSS组合之后呈正向膨胀现象，可见此类“平方根式”组合准则对部分响应存在不合理地放大。因此，在现有SRSS准则框架下，通过引入多维地震响应相关性的影响因素，实现对组合准则计算精度的优化，是兼顾准确性和实用性的可行改进方案。

针对SRSS准则无法考虑多维地震响应相关性的局限性，本文提出并定义多维分量相关系数，该系数能够有效量化多维地震动输入的相关程度，并将此系数引入SRSS准则中，提出能够考虑多维响应相关性的改进组合准则。将改进组合准则运用于球面网壳和鞍型网壳算例的地震反应分析，并将计算结果与时程方法和SRSS准则计算结果进行对比，验证本文准则的适用性与效率。

1 多维地震响应组合准则

1.1 经典反应谱CQC准则

对于具有N个节点的空间结构，在三维地震作用激励下，其动力微分方程可写为

式中：u（t）为地震作用下的结构动力位移；M、K、C分别为质量矩阵、刚度矩阵、阻尼矩阵；ιx、ιy、ιz分别为x、y、z方向的影响因子向量。

运用振型的正交特性，可将式（1）解耦得到：

式中：qn(t)为第n阶振型坐标；kn、ωn、ζn分别为第n阶振型的刚度、频率、阻尼比；r为方向参数，可取为为r方向地震动输入，Γn(r)为r方向第n阶振型参与系数。

在零初始条件下，式（2）的解为

由此推得反应量Qa(t1)和Qb(t2)互相关函数为

式中：hi(t1-τ1)、hj(t2-τ2)为单位脉冲响应函数；为第i、j阶广义振型量；Rpq(τ1，τ2)为p方向和q方向地震加速度分量的互相关函数。

基于此，采用Wiener-Khintchine公式［3］求得反应量的功率谱密度函数为

式中：σNi(p)和σNj(q)分别为p方向第i阶振型响应和q方向第j阶振型响应的标准差为p与q分量输入时第i与j振型响应的相关系数，可写为

式中：Hi(r)和Hj*(r)互为共轭频响函数；Spq(r)为p方向和q方向地震加速度分量的功率谱密度。

假定各分量地震动激励为涵盖结构自振频率的均值为零的平稳随机过程，且结构各振型的响应也是平稳的。此外，与各阶振型的周期相比，地震动持续时间足够长，地震动功率谱密度在主振型频率范围内呈平缓变化，故而可以认为结构整体响应的峰值因子与振型响应的峰值因子近似相等。最终，可得到结构峰值响应估计值为

式（7）即为经典反应谱方法中的多维CQC组合准则。采用式（7）即可通过组合各振型和各方向地震响应，最终得到结构总响应。

采用留数定理［9］在复平面上进行围道积分，并取且ζ=ζi=ζj，可将相关系数最终简化为

至此，对于一维r方向的地震动输入情形，可得到对称结构的峰值响应估计值Q（r）为

1.2 多维响应SRSS准则

在工程实践中，对于空间结构在多维地震动输入下的响应评估，现有的多维反应谱方法和多维推覆分析方法为考虑各阶振型之间的相关性，常采用CQC准则获取地震动各分量单独输入时的地震响应，然后采用SRSS准则将各分量响应组合可得到结构总响应。

将式（9）代入式（7）中，可得：

式中：Q(p)和Q(q)分别为p方向和q方向地震动分量单独输入时的结构峰值响应估计值，ρpq为p方向和q方向地震动分量的相关系数。

依据主轴模型，可进一步假定地震动x、y、z各分量互相独立、互不相关，则各分量的自相关系数均为1，互相关系数均为零，即ρpq应满足：

从而，式（10）可写为

式（11）即为多维地震响应的SRSS组合准则。采用反应谱法或者推覆分析方法，结合式（12）即可得到空间结构的多维地震动响应。

1.3 考虑多维地震响应相关性的MCC准则

由于SRSS组合准则忽略了多维地震响应相关性，因此通常低估空间结构地震响应量。而直接采用多维CQC组合准则［式（7）］须事先求解相关系数［式（6）］，该系数复杂的表达形式和繁冗的计算过程使得与多维CQC组合准则结合后的反应谱方法丧失了计算简洁的优势，因此，多维CQC组合准则远不及SRSS组合准则［式（12）］应用广泛。

为合理考虑地震动输入各分量之间的相关性，本文引入多维分量相关系数ηpq，其表达式为

将多维分量相关系数ηpq引入SRSS组合准则［式（12）］，可得到：

式（14）即为考虑多维地震响应相关性的MCC （Multicomponent Correlated Combination）组合准则。

由式（13）和式（14）可知，多维分量相关系数ηpq的取值范围为0≤ηpq≤1，当地震动各分量相关性较低时，相关系数ηpq趋近于0，MCC准则近似为SRSS准则；地震动各分量相关性越高，相关系数ηpq越大，峰值响应Q越大。采用CQC准则得到地震动各分量单独输入时的地震响应，然后采用上述MCC准则组合各分量响应，在不显著增加计算量的前提下，即可得到结构总响应。

2 多维地震动分量相关性研究

2.1 地震动记录

为研究地震动多维分量的相关性，本节从太平洋地震工程研究中心的NGA强震数据库和日本地球科学与防灾技术研究所的K-NET强震数据库中共选用498条强震记录，其中367条记录于硬土场地，131条记录于软土场地。地震波各方向的加速度反应谱如图1所示。为便于观察，对部分地震波进行调幅，后续分析中仍采用原始地震动记录。

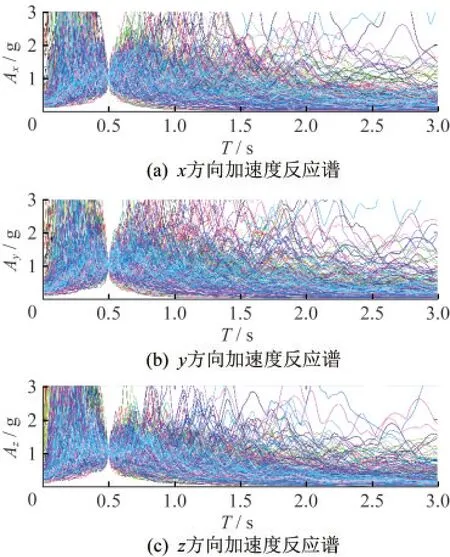
图1 地震动加速度反应谱Fig.1 Acceleration spectrum of earthquake waves

2.2 相关性分析

采用MATLAB对全部498条地震动记录进行多维分量的相关性分析，采用并行计算技术，计算各分量之间的相关系数ηxy、ηyz、ηzx（式（13）），计算值分布热度图如图2所示。观察计算结果可知，水平分量（x与y轴）之间的地震动相关性明显高于水平分量与竖向分量（y与z轴、x与z轴）之间的相关性，且离散性更显著，这一现象表明：

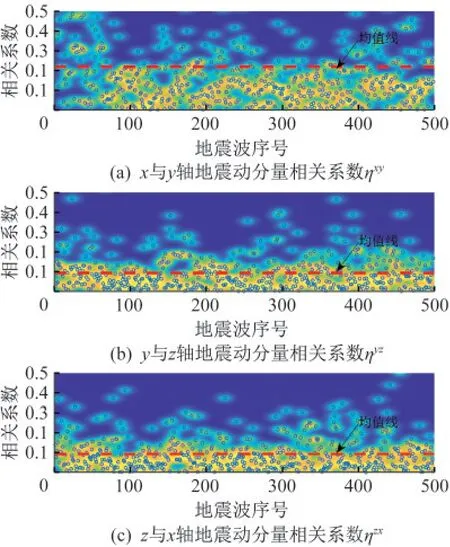
图2 地震动各分量之间相关系数Fig.2 Correlation coefficient of seismic multicomponent

（1）实际地震波的主轴方向各异，水平方向的两主轴与地震动记录台站自身标定的主轴存在一定夹角。一般而言，地震动记录台站的自身主轴在设立之初即已标定，不随地震动是否发生、地震波是否抵达而变化，因此，实际地震波抵达台站时，地震动水平方向的两主轴与台站的标定主轴一般不会恰好吻合，天然地存在一定夹角，造成水平分量之间存在一定相关性。

（2）竖直方向的主轴与台站自身主轴夹角的差别并不明显。据观测统计，近年来数次强震的震源深度仅在20 km以内［12］，与之相比，地震动台站的震中距一般可达几十或上百余公里，这使得地震波竖向主轴与台站自身主轴的夹角较小，因而水平分量与竖向分量（y与z轴、x与z轴）之间的相关性较低。

尽管由于主轴夹角的存在，水平分量之间的相关系数ηxy比水平分量与竖向分量之间的相关系数ηyz、ηzx更高，但总体而言，由于地震波传播过程中经过多层土、远距离的折射、滤波作用，地震动各分量之间的相关性仍然不高（相关系数平均值小于0.3），这说明早期采用忽略多维地震动相关性的SRSS组合准则存在一定的合理性。然而，由于SRSS组合准则给出的计算结果普遍低于实际地震响应，在工程应用中很可能给出偏不安全的预测结果，大大降低了结构实际的计算可靠度。因此，采用本文提出的MCC组合准则，科学地考虑多维地震动相关性，针对性地弥补现有组合准则的不足，有助于更精细化地分析结构响应，保证空间结构多维地震响应组合的计算可靠度。

3 算例分析与讨论

为验证MCC准则的适用性及计算效率，采用ANSYS和MATLAB对两个典型网壳结构算例进行三维动力分析，并以节点位移作为对比参数，将分别采用MCC准则和SRSS准则组合得到多维地震响应与直接采用三维动力分析得到的计算结果进行对比，分析误差和效率，验证MCC准则的适用性。

本文选用1952年美国KernCounty地震的Taft地震波三向分量作为地震动输入，Taft地震波的各分量相关系数为ρxy=0.37、ρyz=0.13、ρzx=0.11，各分量相关性较强，为充分激励结构弹塑性响应，取调幅系数1.5。

3.1 结构模型

K6型单层球面网壳结构跨度为60 m，矢跨比为1/7，采用焊接球节点，底部为固定铰支座，如图3所示。直纹型单层鞍型网壳结构跨度60 m，矢跨比为1/7，采用焊接球节点，周边四边支承为固定铰支座，如图4所示。对网壳结构施加满跨均布荷载，其重力荷载代表值为1.5 kN/m2，并转化为节点集中质量以考虑其惯性力效应。在满足静力设计的要求下，全部结构构件均采用圆钢管，球面网壳主肋杆采用ϕ140×5，环杆和斜杆采用ϕ121×4；鞍型网壳直杆和斜杆均采用ϕ180×6。构件材料为Q235钢，采用双线性随动强化模型，弹性模量206 GPa，屈服强度235 MPa，屈服后弹性模量0.8 GPa。采用Rayleigh阻尼，阻尼比为0.02。采用“一杆两单元”模型模拟杆件屈曲效应，对网壳施加幅值为200 mm的一阶模态初始缺陷。

图3 球面网壳模型Fig.3 Spherical latticed shell layout

图4 鞍型网壳模型Fig.4 Saddle latticed shell layout

3.2 时程分析组合结果对比

采用时程法计算球面网壳分别在x、y、z一维输入下的位移响应，再由SRSS准则和MCC准则分别组合得到多维响应（USRSS、UMCC），其结果与直接对结构进行三维时程分析得到的多维位移响应（U3D）作对比，如图5、图6所示。为便于对比结构峰值响应的计算精度，图5中的节点号按节点位移数值大小排序，且仅给出位移最大的前100个节点位移结果。观察图5、图6的响应分布和变化趋势可知，SRSS准则和MCC准则的计算结果变化趋势相近，SRSS准则结果总体比时程法计算结果偏小，而MCC准则结果曲线更接近时程法结果曲线，并在其上下波动。观察最大位移响应可知，相比三维时程分析结果，SRSS准则的各方向计算误差分别为27.5%、15.4%、24.4%，MCC准则的计算误差分别为10.6%、4.33%、11.3%，MCC准则的计算精度比SRSS准则分别提高61.5%、71.8%、53.7%，效果显著。

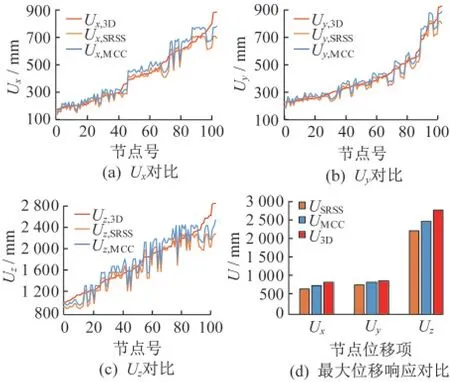
图5 球面网壳计算结果对比Fig.5 Comparison of results of spherical latticed shell

图6 球面网壳节点合位移云图对比（单位：mm）Fig.6 Comparison of nodal resultant displacement of spherical latticed shell （Unit：mm）

图7给出了鞍型网壳的计算结果对比，仅取位移最大的前80个节点计算结果作为对比参考量。图8给出了鞍形网壳节点合位移云图。观察图7、图8的响应分布和变化趋势可知，三种方法计算结果的变化趋势相近，SRSS准则结果总体比时程法计算结果偏小，而MCC准则结果曲线更接近时程法结果曲线。观察最大位移响应可知，相比三维时程分析结果，SRSS准则的各方向计算误差分别为9.9%、9.2%、16.0%，MCC准则的计算误差分别为4.8%、4.9%、7.93%，MCC准则的计算精度比SRSS准则分别提高51.8%、47.4%、50.6%，效果显著。

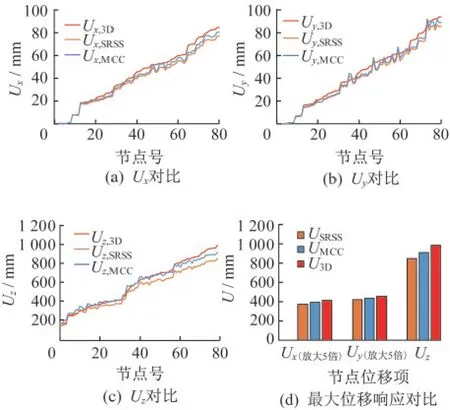
图7 鞍型网壳计算结果对比Fig.7 Comparison of results of saddle latticed shell

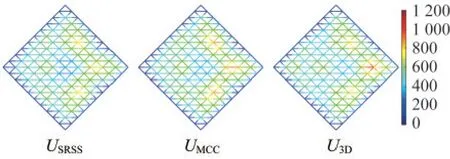
图8 鞍形网壳节点合位移云图对比（单位：mm）Fig.8 Comparison of nodal resultant displacement of saddle latticed shell （Unit：mm）

时程分析的计算结果对比表明，MCC准则的计算精度较高，最大节点位移的计算误差均控制在12%以内，能够合理预测位移响应的分布规律和变化趋势，显著改善了SRSS准则组合时程法结果时低估多维响应的缺点。

3.3 推覆分析组合结果对比

采用以振型矢量为荷载的推覆分析计算球面网壳的一维响应，通过SRSS准则和MCC准则组合得到多维响应，并与三维时程分析计算值作对比，如图9所示。观察曲线可知，MCC准则的结果曲线更加稳定平缓，更接近时程法的结果曲线，而SRSS准则结果整体比时程法计算结果偏小，且曲线波动剧烈，离散程度较高。观察最大位移响应可知，相比三维时程分析结果，SRSS准则的各方向计算误差分别为40.4%、37.7%、29.8%，MCC准则的计算误差分别为14.6%、8.95%、10.8%，MCC准则的计算精度比SRSS准则分别提高63.8%、76.3%、63.8%，效果显著。

图9 球面网壳计算结果对比Fig.9 Comparison of results of spherical latticed shell

图10给出了鞍型网壳的计算结果对比。观察可知，SRSS准则结果总体比时程法结果偏小，且更加离散，而MCC准则结果更接近时程法结果，计算稳定。观察最大位移响应可知，相比三维时程分析结果，SRSS准则各方向计算误差分别为18.0%、16.8%、36.3%，MCC准则的计算误差分别为9.46%、8.05%、12.5%，MCC准则的计算精度比SRSS准则分别提高47.6%、52.2%、65.6%，效果显著。

图10 鞍型网壳计算结果对比Fig.10 Comparison of results of saddle latticed shell

推覆分析的计算结果对比表明，MCC准则的计算精度较高，最大节点位移的计算误差均控制在15%以内，能够合理预测位移响应的分布规律和变化趋势，显著改善了SRSS准则组合推覆法结果时低估多维响应的缺点。限于篇幅，本文不再给出推覆分析计算得到的节点位移云图。

3.4 误差统计分析

采用并行计算技术，对球面网壳和鞍型网壳进行时程分析，统计结构在498条地震动输入下的最大位移响应，计算得到相对误差频率分布如图11、图12所示。观察结果可知，对于球面网壳，采用SRSS准则的位移误差值主要分布于20%～30%，最大误差超过40%，而采用MCC准则的位移误差值集中于15%以内，大部分算例误差控制在30%以内；对于鞍型网壳，采用SRSS准则的位移误差值主要分布于10%～20%，最大误差超过30%，而采用MCC准则的位移误差值集中于10%以内，大部分算例误差控制在25%以内。计算结果表明，MCC准则能够显著提高空间结构最大位移响应的计算精度，且x、y、z方向位移的误差水平相近，稳定高效。

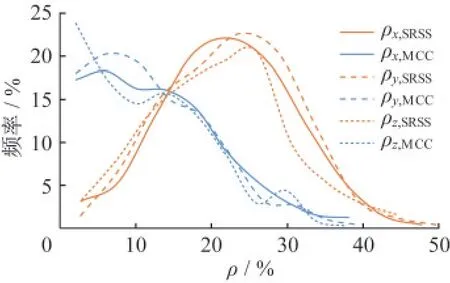
图11 球面网壳误差频率分布图Fig.11 Frequency distribution of error of spherical latticed shell

图12 鞍型网壳误差频率分布图Fig.12 Frequency distribution of error of saddle latticed shell

3.5 计算效率对比

与SRSS准则相比，MCC准则仅需额外进行地震动多维相关性分析，得到一组具有统计意义的相关系数，其余计算步骤与SRSS准则一致。采用MATLAB编制相关性分析程序，MCC准则额外消耗的计算代价可以忽略不计。此外，基于大量地震动记录，分析得到不同场地条件下地震动多维相关系数的可靠统计值，MCC准则将更具计算优势。