水热耦合模拟中的冻土渗透系数模型选择

王青林， 陈 磊， 明 锋

（1. 青海省湟源公路工程建设有限公司， 青海 西宁 810000； 2. 青岛农业大学 建筑工程学院，山东 青岛 266000；3. 中国科学院 西北生态环境资源研究院 冻土工程国家重点实验室， 甘肃 兰州 730000）

0 引言

我国是第三冻土大国，冻土区面积约占全国面积的53.5%［1］。受冻土区气温变化的影响，不仅土中原位水发生相变产生约9%的体积膨胀，而且未冻结土层中的孔隙水在温度梯度作用下将向冻结锋面迁移并冻结成冰。由此将引起地表出现大幅度隆起，局部变形量甚至超过40 cm，这将导致修建在寒区环境中的建筑物产生冻害［2-4］。为解决因冻胀引起的冻害问题，研究者提出了诸多水热耦合模型来评估冻胀［5-7］。在这些冻胀模型中，冻土渗透系数是控制水分迁移速率及迁移量的关键参数。因此，选择合理的渗透系数模型就成为准确预测冻胀的前提条件。

获取冻土渗透系数的方法有两种：试验测试和理论推导。尽管饱和冻土渗透系数试验存在费时、费力、离散性大等缺陷，但诸多研究人员仍得到了冻土渗透系数随温度的变化规律［8-12］。基于已有试验结果，国内外学者提出了一系列经验模型和理论模型来弥补试验方法的不足。经验模型的特点是形式简单，但没有严格的推导过程，仅仅是根据试验结果所给出拟合公式，通常具有一个或多个经验参数［13］。而且，经验模型中冻土渗透性系数是未冻水含量或者温度的函数。在水热耦合模型中，大多采用经验模型来描述冻土渗透系数变化规律，如应用较多的冰阻模型［7］。该模型认为饱和冻土的渗透系数由于受到了冰的阻力作用，致使其降低至相同液态水含量条件下非饱和未冻土渗透系数的1/I（I是冰阻系数，其常为含冰量或温度的函数）。经验模型中的参数是通过试验结果拟合得到，所以这些参数仅适用于特定土体。当将其用于其他土体时，模型有效性将有所降低［14］。所以，在不同水热模型中，通常会选择不同的经验模型来提高预测精度。相对而言，理论模型具有严格的推导过程，其模型参数具有明确的物理意义。由于理论模型减少了对经验系数的依赖，其普适性更强，更值得在水热模型中推广使用。因此，本文对冻土渗透系数理论模型在水热耦合模型中的有效性进行讨论。

由于水热耦合模拟结果对冻土渗透系数极为敏感，所以合理选择冻土渗透模型就变得十分重要。为评价理论模型在水热耦合模型中的适用性，本文以四组饱和冻土的渗透系数理论模型为例，首先将渗透系数理论模型与经验模型预测结果进行对比，然后选择预测效果较好的渗透系数模型带入水热耦合模型，以冻胀量变化为判据评价其适用性。

1 冻土渗透系数理论模型

在冻土渗透实验的基础上，人们提出了诸多经验模型及理论模型，表1 列举了四组饱和冻土的渗透系数理论模型。根据模型特点，将四组模型分别命名为分形模型［13］、离散统计模型［14］、连续统计模型［15］和等价模型［16］，各模型的数学表达式及主要计算参数如表1所示。

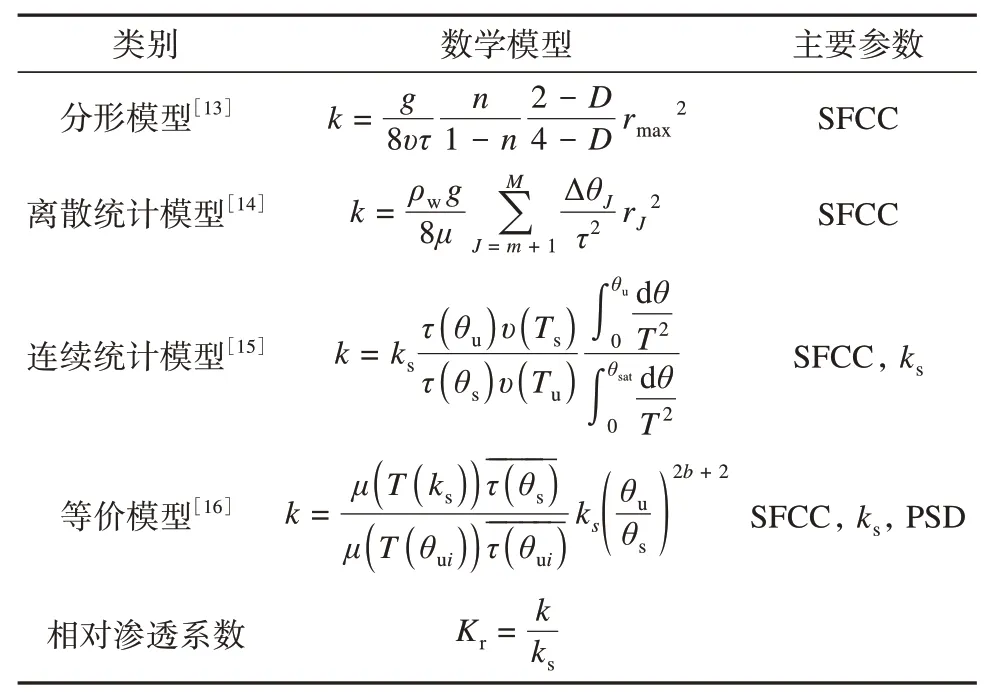
表1 冻土渗透系数模型Table 1 Hydraulic conductivity models for frozen soil

上述四组模型的详细推导过程，可参阅文献［13-16］。为更好体现四组渗透系数模型的优缺点，下面对四组理论模型进行简单介绍。分形模型是将分形理论应用到冻土中，可更好地表征土中孔隙真实无序的状态。该模型结果主要取决于冻土中的最大孔径，孔隙率、孔径分维数和迂曲度，其中最大孔径对冻土的渗透系数影响最大［13］。离散统计模型是基于土体冻结特征曲线与土体孔隙分布函数的相似性，以及非饱和土的渗透系数与土水特征曲线之间的关系而提出的，该模型的计算结果主要取决于其中有效孔隙分布［14］。连续统计模型则是通过建立冻结特征曲线和孔径分布函数的关系函数，提出了渗透系数模型，该模型只需要对不同未冻水含量条件下的土体冻结特征曲线进行积分即可得到渗透系数［15］。等价模型借鉴非饱和土的渗透系数模型，认为孔隙冰与空气对水分迁移的阻碍作用是相当的，认为饱和冻土的渗透系数等于相同液态水含量条件下非饱和未冻土的渗透系数［16］。由于部分文献中并没有给出饱和未冻土的渗透系数，所以只能计算其相对渗透系数进行比较。当采用相对渗透系数表述预测结果时，只需要土体冻结特征曲线和土体颗粒级配曲线。

为量化渗透系数预测值和实测值之间的差异，采用均方根误差（RMSE）进行分析，其计算公式如下：

式中：N是实测数据数量；Krti是第i个实测相对渗透系数（由经验模型确定）；Krpi是第i个预测相对渗透系数（由理论模型确定）。

2 结果与分析

为评价渗透系数理论模型的适用性，此处选取文献［17-19］中的三个水热耦合模型为例进行分析。在这三组水热耦合模型中，不仅都采用的是饱和冻土的渗透系数经验模型，而且文献中都给出了详细的模型参数。模型验证从两个方面开展：渗透系数变化和冻胀变化。为方便比较，将案例一、案例二和案例三中的渗透系数经验模型分别命名为经验模型一，经验模型二和经验模型三。

2.1 渗透系数变化

2.1.1 案例一

案例一为文献［17］中的水热耦合模型，该模型采用经验模型一来描述冻土渗透系数变化。经验模型一可以表示为［20］：

式中：k为饱和冻土的渗透系数；ks为饱和未冻土的渗透系数；θu为体积未冻水含量；θ为初始饱和体积含水量；b为与土颗粒级配相关的拟合参数，可以表示为：

式中：dg为几何平均颗粒直径；σg为几何标准差；dg与σg可由土颗粒级配曲线获得。

基于文献［17］中给出的土体冻结特征曲线、土颗粒级配曲线和饱和渗透系数，利用表1中的模型，可计算得到四组模型计算的相对渗透系数（图1）。从图1可以看出本文所列举的四组理论模型可以有效反映渗透系数随温度的变化规律，且预测值与文献［17］中的渗透系数值比较接近。应该指出的是，分形模型存在有效的临界温度，对应冻结过程中的粉质黏土、粉土和粉砂分别是-18.0 ℃、-15.0 ℃和-13.7 ℃。当温度低于该临界温度时，分形模型将不再适用。从图1 中的计算结果来看，该临界温度较低，可满足冻土渗透系数计算要求。离散统计模型高估了粉质黏土的渗透系数，但低估了粉砂土的渗透系数。整体而言，分形模型、等价模型和连续统计模型的表现较好。

图1 不同土体的相对渗透系数随温度变化Fig. 1 Variation of the relative hydraulic conductivity with the temperature

图2 进一步在双对数坐标中对比了渗透系数模型计算值和文献［17］中所用的渗透系数值。在《土工试验方法标准》（GB/T 50123—2019）中，土体渗透系数的最大试验允许差值为±2×10-n（n为自然数）。参考此误差标准，本文确定相对渗透系数预测值的可接受试验误差值为±2×10-n。如图2 所示，大多数的数据点都落在可接受试验误差区域内，仅少部分数据点落在可接受实验误差区域外。需要注意的是，有三组渗透系数数据点甚至落在一个数量级误差区域外，如粉砂的分形模型，粉土和粉砂的离散统计模型。总体而言，本文所列四组渗透系数模型预测值和文献［17］水热耦合模型中所用的渗透系数值较接近。这表明本文所列四组渗透系数理论模型可代替文献［17］中的经验模型。

图2 文献［17］所用相对渗透系数与四组理论模型计算值对比Fig. 2 Comparison of the relative hydraulic conductivity used in Reference ［17］ and the values calculated by the four hydraulic conductivity models

表2汇总了这四组模型的均方根误差值。可以看出，四组模型的均方根误差值均较小，说明了四组模型具有良好的稳定性。四种模型均对粉砂的预测效果较差，对粉土和粉质黏土的效果较为准确。等价模型的均方根误差最小，其次是连续统计模型、分形模型和离散统计模型。对于文献［17］中的土样，等价模型的预测能力最好。

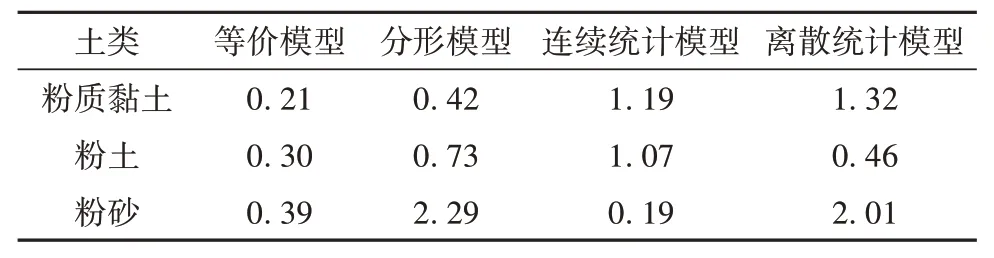
表2 模型的均方根Table 2 RMSE of the model

2.1.2 案例二

案例二以文献［18］中的水热耦合模型为例进行分析，并以粉质黏土为研究对象。文献［18］中使用的渗透系数为经验模型二，其表达式为：

式中：模型所需参数可查询参考文献［18］。

图3对比了四组理论模型预测值与文献［18］所用的相对渗透系数。如图所示，相对渗透系数经验模型值与分形模型和离散统计模型的预测值较为接近，但是与连续统计模型和等价模型的预测值稍有偏差。鉴于该经验模型预测结果位于本文四组模型预测范围内，且被O’Neill 等［21］、周国庆等［22］、周扬等［23］多次采用，表明该模型具有一定的合理性。需要指出的是，该模型的指数对不同土并不是一个常数。对于等价模型，根据颗粒级配曲线计算得到其指数n=12.08，与文献［18］所用的n=9 有所差别，所以导致相对渗透系数预测值偏低。对分形模型，该粉质黏土分形模型有效的临界温度是-22 ℃，低于该温度则分形模型不再适用。可以看出，土体颗粒级配曲线不仅严重影响等价模型中的指数n的取值，而且对土体冻结特征曲线的数值和形态也有较大影响，进而影响分形模型、离散统计模型和连续统计模型的预测精度。

图4 在双对数坐标中对比了四组理论模型与经验模型二的渗透系数预测结果。从图4 中可以看出，只有分形模型和离散统计模型的数据点落在了可接受试验误差区域内，等价模型的数据点则大多落在了可接受实验误差区域的边缘。连续统计模型的数据点虽然大多落在了可接受实验误差区域外，但也基本分布在一个量级的误差区域内。因此，可以采用分形模型和离散统计模型来代替经验模型二。

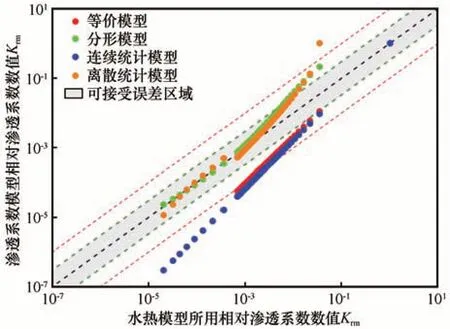
图4 文献［18］中所用的相对渗透系数与四组理论模型计算值对比Fig. 4 Comparison of the relative hydraulic conductivity used in Reference ［18］ and the values calculated by the four hydraulic conductivity models

表3 汇总了这四组模型的均方根误差值，可以看到四组模型的均方根误差值均较小，说明四组模型的稳定性较好。相对而言，分形模型和离散统计模型的均方根误差较小，表明这两组模型可以代替经验模型二。

表3 模型的均方根Table 3 RMSE of the model

2.1.3 案例三

案例三以文献［19］的水热耦合模型为例进行分析。该耦合模型采用的是经验模型三，其表达式为：

从公式（5）可以看出，经验模型三的表达式简单，只需要温度和饱和渗透系数就可以预测冻土渗透系数。图5给出了本文所列举的渗透系数模型计算的相对渗透系数。如图所示，除等价模型外，其余三组理论模型与经验模型三的渗透系数预测值较为接近。需要指出的是，该粉质黏土对应的分形模型有效临界温度为-1.40 ℃。对比前两个案例，此粉质黏土的分形有效临界温度偏高，这是因为该土样的冻结特征曲线斜率过大，使得大部分水分被迅速冻结。等价模型与经验模型三的预测结果相差最大，可能是由于土体颗粒级配曲线不合理，导致计算得到的指数n偏离极大所致。尽管经验模型三存在经验参数，但仍适用于描述此粉质黏土样品渗透系数变化。

图5 相对渗透系数随温度的变化曲线Fig. 5 Variation of the relative hydraulic conductivity with the temperature

图6 进一步在双对数坐标中对比了本文所列举的四组渗透系数模型和经验模型三计算的相对渗透系数数值。如图6 所示，连续统计模型的数据点基本都落在可接受试验误差范围内；分形模型的数据点也大多落在可接受试验误差区域内；离散统计模型只有少部分数据点落在可接受试验误差内，但是大部分都落在了一个量级的误差区域内；等价模型预测结果则几乎全部不在可接受试验误差区域内。这说明等价模型并不适用于此土样，而其余三组理论模型可以代替经验模型三建立冻土渗透系数变化趋势。

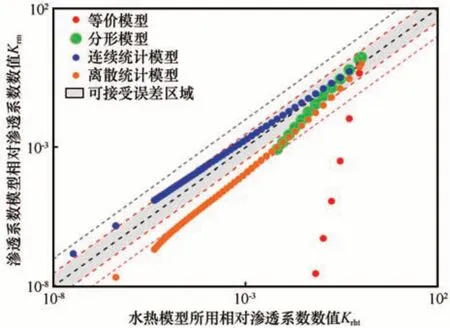
图6 文献［19］中所用的相对渗透系数与四组模型计算值对比Fig. 6 Comparison of the relative hydraulic conductivity used in Reference ［19］ and the values calculated by the four hydraulic conductivity models

表4汇总了这四组模型的均方根误差值。由表4 可见，除了等价模型，其余三组模型的均方根误差值均较小，说明了这三组模型的可靠性。其中，连续统计模型的均方根误差最小，其次为分形模型和离散统计模型，而等价模型的均方根误差最大。因此，可以采用分形模型和连续统计模型预测该冻结粉质黏土样品的渗透系数。

表4 模型的均方根Table 4 RMSE of the model

2.2 冻胀变化规律

冻土渗透系数模型大多应用于预测冻土中的水热分布及冻胀、融沉变形。从前一节的分析结果来看，分形模型在三个案例中的适用性更强。因此，本节采用分形模型代替文献［18］中的经验模型二，并利用原文中的相关参数对冻胀试验结果进行预测（图7）。如图7 所示，在冻结前期（0～50 h），无论是经验模型二还是分形模型，其预测的冻胀量与实测冻胀量相差很小。在冻结后期（50～90 h），经验模型二的预测结果偏小，而采用分形模型的预测结果偏大。由于经验模型二的渗透系数预测值略小于分形模型的预测值，所以采用分形模型的冻胀预测结果偏大。但从冻胀预测误差来看，分形模型的预测结果接近实测值（最大相对误差小于10%），可证明分形模型的有效性。

图7 不同渗透系数模型下的冻胀量预测结果Fig. 7 Prediction of the frost heave with different hydraulic conductivity models

3 讨论

3.1 理论模型的优缺点

从三个案例来看，本文所列四组理论模型可以有效的反映文献中渗透系数的变化规律，而且冻胀算例也证实了理论模型的可靠性。由于选择不合理的冻土渗透系数模型，将导致水热分布预测结果不准确，进而影响冻胀预测精度。因此，若在水热耦合模型中，采用渗透系数理论模型，不仅可有效避免经验公式参数的选取，而且还能保证预测精度。但需要注意的是，渗透系数理论模型也存在一定的局限性：（1）最大孔径对分形模型的预测结果影响较大，且该模型存在温度下限，但该下限可满足冻胀模型的要求；（2）离散统计模型虽然解决了分形模型的缺点，但其计算结果并不是一条平滑曲线，难以通过一个公式拟合，因此很难应用到数值计算中。（3）连续统计模型所需参数较少，但对部分土体的适用性较差。（4）等价模型不仅没有严格的理论推导，而且对部分土体的预测效果较差。从四组模型对三个案例的预测结果来看，不同理论模型表现出不同的预测效果，而分形模型在三个案例中表现较为均衡，其适用性最强。因此，建议在水热耦合模型中采用分形模型来描述冻土渗透系数变化。

3.2 冻融过程中的渗透系数滞后性

从表1 中可以看出，冻土渗透系数不仅可以采用温度为变量，而且也可以采用未冻水含量为变量。图8 以经验模型一（Tarnawski 和Wagner 模型）为基础，计算得到冻结与融化过程中的土体相对渗透系数变化规律［20］。如图8 所示，在相同温度条件下，计算得到的粉质黏土的相对渗透系数最大，其次是粉土，粉砂的相对渗透系数最小；而在相同体积未冻水含量下，正好相反，粉砂的相对渗透系数最大，其次是粉土，而粉质黏土的相对渗透系数最小。这是因为Tarnawski 和Wagner 模型中，土体冻结特征曲线和土体颗粒级配曲线共同决定了渗透系数的大小。土体颗粒级配曲线不仅决定了模型参数2b+ 3 的大小，而且也影响土体中的未冻水含量θu。依据土体颗粒级配曲线，计算得到粉质黏土，粉土和粉砂的模型参数2b+ 3 分别是12.22、10.83和8.52。如图8（a）所示，计算出来的融化过程的渗透系数要小于冻结过程的渗透系数，这是因为土体在融化过程中的未冻水含量要小于其在冻结过程中的未冻水含量。但是随着温度的降低，滞后效应对渗透系数的影响也在逐渐减小。但是采用未冻水含量为变量时，渗透系数在冻融过程并没有体现出滞后效应［图8（b）］，这和以往的研究结果一致［24］。因此，建议以未冻水含量为变量表示冻土渗透系数模型。

图8 冻结和融化过程中相对渗透系数随温度（a）和体积未冻水含量（b）的变化曲线Fig. 8 Variation of the relative hydraulic conductivity with the temperature （a） and unfrozen water content （b） during the freezing and thawing process

4 结论

本文通过对四组饱和冻土的渗透系数模型和三个水热耦合模型中选取的经验模型的计算结果进行对比，讨论了四组饱和冻土的渗透系数模型的预测能力，得出以下主要结论：

（1）水热耦合模型中所用的渗透系数经验模型数值和本文所列举的四组理论模型数值大多都非常接近，建议使用渗透系数理论模型来描述冻土渗透系数变化规律。

（2）四组理论模型均能有效描述冻土渗透系数变化，但理论模型预测结果受土体颗粒级配曲线影响明显，推荐使用分形模型计算冻土渗透系数。

（3）用温度表示的渗透系数表现出滞后效应，而用未冻水含量表示的渗透系数并没有表现出滞后效应，建议在冻土渗透系数模型中以未冻水含量为变量。