基于和声遗传算法的铝件铸造线布局优化研究

孙永奇，袁 亮，肖文东，崔健平，刘 超

（1.新疆大学商学院，新疆乌鲁木齐 830046；2.新疆大学智能制造现代产业学院，新疆乌鲁木齐 830046）

我国是制造业大国，根据国家统计局2023年5月数据显示，自2023年4月以来我国汽车产量同比增长59.8%，比3月加快48.6%[1]。新能源汽车的产量增长，带来的是相对应的零配件制造企业订单量的增长，产能不足促使相关制造企业想办法提高产能，或迅速投资建设新工厂以抢占市场份额促进企业发展。做好前期的铸造车间的布局可以帮助企业减少各工序间的搬运时间，降低制造成本，提高工厂的核心竞争力。

近年来由于计算机的发展，关于启发式算法目前学术界也有较多研究内容可供参考。张超等[2]使用遗传算法及模拟退火算法对生产线布局进行物流成本最小优化；赵川等[3]将模拟退火算法与遗传算法相结合，证明此类方法可以有效解决工厂布局的NP 问题。赵鸿飞等[4]在和声算法中引入自适应参数的调节方式可以解决离散性数学问题，并且解决了和声算法方向性差的缺点。

结合上述研究现状，针对和声算法初始解产生质量较差但有较好的收敛性，而遗传算法具有较好的初始解、全局寻优能力强但收敛性较差的特点，将遗传算法与和声算法相结合，利用遗传算法生成的新的种群作为和声算法的初始解，增加找到目标函数最优解的概率，得到在工厂布局优化中的满意结果。

1 铸造线布局模型建立

文章以某公司汽车转向节铸造车间为例，对铸造线的优化布局模型做出以下几点设定。

（1）车间内各工作单元是平面关系。

（2）车间内各工作单元形状都是矩形。

（3）车间内各工作单元长和宽平行，并且其与墙壁（即x轴、y轴）分别平行。

相关的数学模型如图1所示。

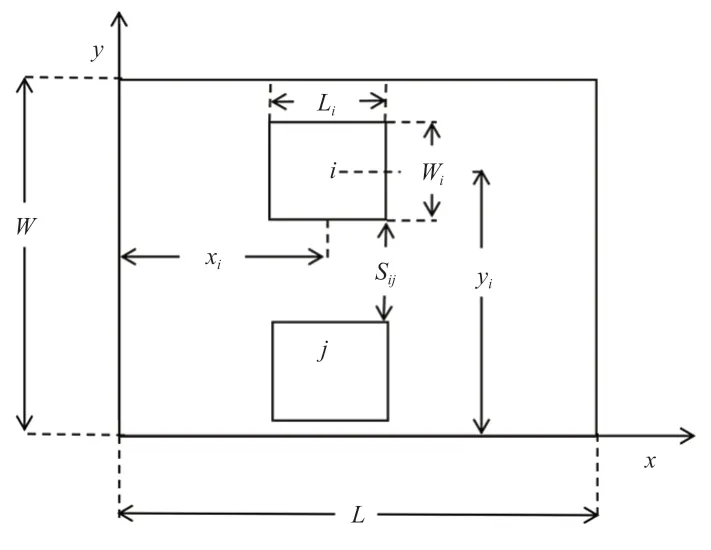
图1 转向节铸造线模型

其中，不同工作单元用不同序号表示。L为车间总长，Li为第i个单元区域长度，W为车间总宽，Wi为第i个单元区域宽度，Xi、Yi分别为第i个单元中心点横坐标与纵坐标，Sij为相邻i、j两个单元间的距离。

以工厂需求物流成本最小化优化目标，建立的物流成本最小化目标函数如下：

式中，C为总搬运成本，Cmin为最小物流成本，cij为车间内第i个单元与第j个单元间的搬运成本，fij为车间内第i个单元与第j个单元间的搬运频率，dij为车间内第i个单元与第j个单元间的曼哈顿距离。

针对工厂实际应用情况仍然需要对数学模型建立如下几点约束条件。

（1）车间各单元间与墙壁距离要保留2 m 的通道空间供物流搬运使用，公式如下：

（2）车间各单元间需保留2 m 的通道距离，公式如下：

（3）在同一行或同一列的单元总长度不能超过车间总长或宽，公式如下：

（4）一个单元在布局中只能出现一次，公式如下：

（5）单元坐标和单元间的间距非负性，公式如下：

2 和声遗传算法设计

和声算法随机产生和声库HM，通过取值概率HMCR 在和声库中对新解随机搜索，并且用微调概率PAR 对新解进行局部的调整。最后对比新解与目标函数值的优劣，如果是优，则对和声库进行更新；如果是劣，则继续迭代过程，直至达到最大迭代次数。和声算法收敛速度快，但精度较低，且初始解的好坏是随机的。

遗传算法编码简单且受约束条件影响较小。目前遗传算法在神经网络、排列优化、生产调度等领域广泛应用。遗传算法全局搜索能力强，但后期收敛较慢且局部寻优能力不足。

针对和声算法和遗传算法的特点，利用遗传算法生成次优初始种群，然后利用和声算法对该种群进行搜索优化出质量较好的新种群。

2.1 编码

关于启发式算法的布局优化，目标函数是解决布局的搬运成本最优排列序列。14个单元的设备编码设计为：（X1、X2、X3、……、X14），其中，（1,2,3,4,……,14）为设备标号。

2.2 初始化和声记忆库

初始化的和声库应在其解空间具有一定的分散性和随机性，其函数定义如下：

初始化后的和声记忆库结构如下：

在该种群中，i为和声记忆库大小，n为种群规模。同时，计算各个和声的适应度，选取适应度最优的和声记为最美和声。

2.3 遗传算法更新和声记忆库

随机生成新和声的过程中，需要确保生成的和声符合问题的约束条件和解空间。同时，生成的和声应该能够涵盖问题的搜索空间，以便在优化过程中获得更多的可能解。

具体步骤为在初始化后的和声记忆库中使用遗传算法随机选择两条和声记录，使其交叉变异生成新的和声并计算该和声的适应度，如果这个和声的适应度比和声记忆库中的和声适应度更优秀，那么就将该和声替换掉和声库里的原有和声。同时，若这个和声的适应度优于最美和声适应度，那么就将该和声标记为最优和声。

2.4 算法终止条件

判断该和声遗传算法是否达到最大迭代次数N，达到则算法结束，输出和声最优结果；未达到则继续和声算法进行迭代。

3 铸造线布局应用及结果

3.1 应用

对上述公司汽车转向节铸造线布局物流成本优化，首先对铸造线现有各单元区域面积数据进行收集，具体面积信息见表1。

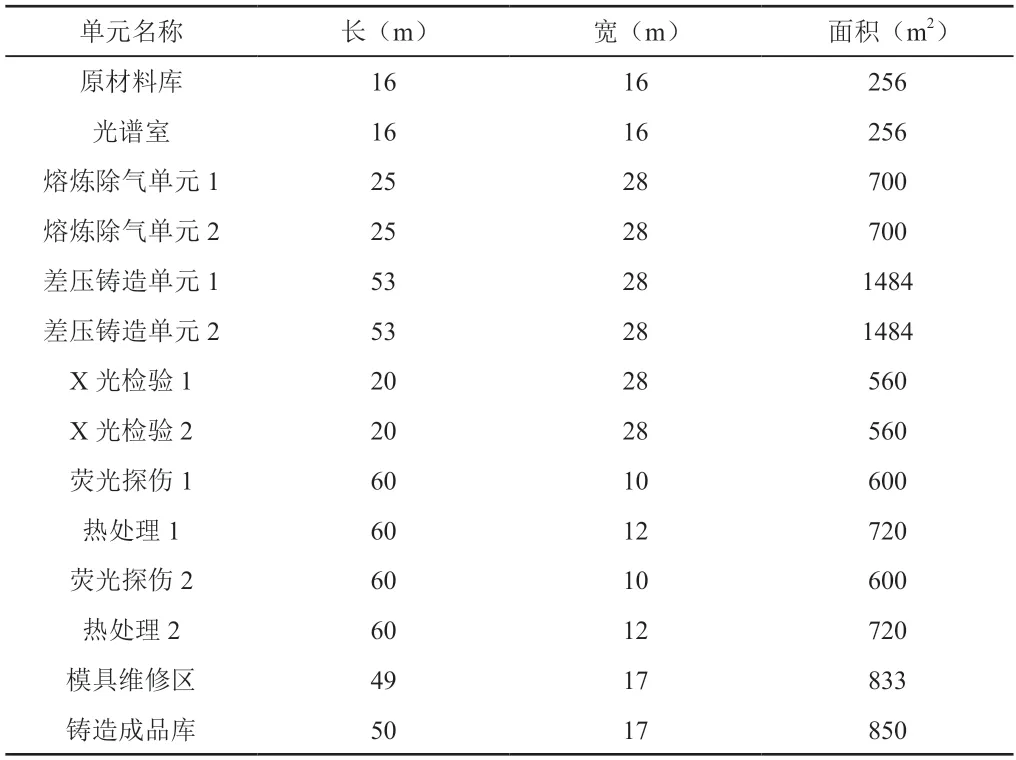
表1 铸造车间单元信息

对搬运频率及搬运成本进行统计，车间内搬运成本为0.001元/kg·m，分别制订搬运频率、搬运单价矩阵公式如下：

通过研究现有参考文献[5-6]，HMCR 取值较大时对算法的局部收敛更有益，取值较小时群体的多样性更优。PAR 微调概率越大的值越有利于跳出局部极值，越小的值越有利于算法的寻优，因此本次算法测算设HMCE=0.8，PAR=0.9。设置最大迭代次数为1000次。

3.2 结果

运行算法得出，最优解的染色体集是：14，7，8，5，12，3，1，2，13，6，11，4，10，9。最优解单元中心点位置是：27，11；64，16；86，16；125，16；32，38 ；166，16 ；189，10 ；189，28 ；89，41 ；142，46；32，51；183，52；32，64；94，67。算法迭代曲线及最新布局如图2、图3所示。

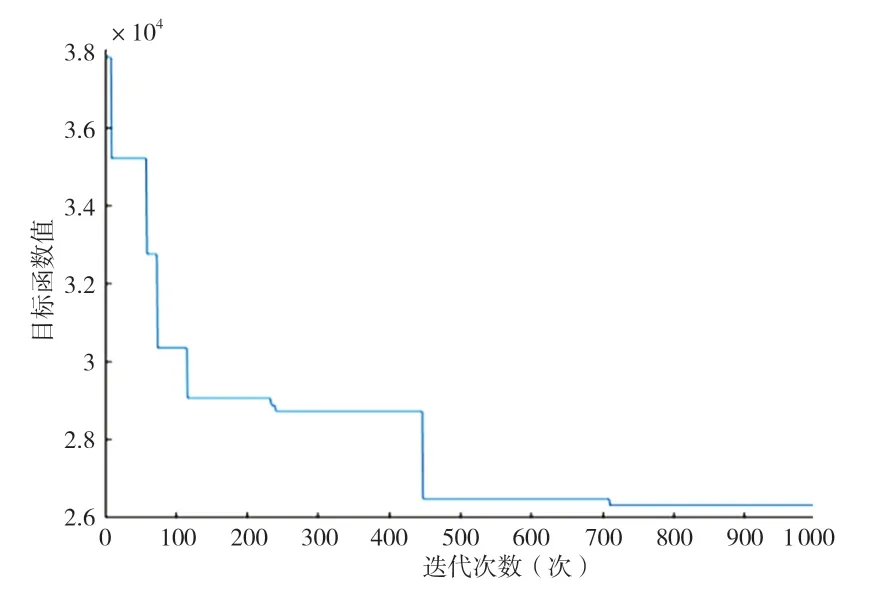
图2 算法适应度曲线

图3 最新布局

和声遗传算法优化后搬运成本计算结果为26324.0 元/班；优化前单元布局各单元中心点为：19，35；11，11.5；34.5，38.5；34.5，80；88，38.5；88，80；126.5，38.5；126.5，80；169，29；169，46.5；169，70.5；169，88；94.5，11.5；167，11.5。

将优化前单元布局中心点位置输入上述成本计算方法中，可得出优化前铸造线物流成本为81 184.9元/班；使用上述生产线数据使用遗传算法通过相同的迭代次数可以得到遗传算法计算出的优化后的物流成本为32 624.4元/班，遗传算法优化后物流成本降低59.81%，而和声遗传算法优化后物流成本降低67.85%。对比优化结果可以确定，和声遗传算法在铸造线布局优化中降低成本效果较好。

4 结束语

文章以某公司汽车转向节铸造车间为例，收集调研铸造线物流现状，建立车间布局数学模型，以物流成本最小作为布局优化目标函数，并且使用和声遗传算法对最优布局方案求解。结论表明，使用和声遗传算法降低该公司铸造线物流成本比遗传算法更有效，可为同类型企业布局方案提供参考。