基于函数型主微分与主成分的岭回归模型与应用
2023-11-24高海燕
高海燕,张 悦
(1.兰州财经大学 统计学院,甘肃 兰州 730020;2.甘肃省数字经济与社会计算科学重点实验室,甘肃 兰州 730020)
0 引言
随着互联网技术的快速发展以及数据收集技术的不断进步,大量复杂连续数据应运而生.对于如何高效处理这些高频连续数据并探究其内在规律性, Ramsay[1]提出函数型数据分析方法(Functional Data Analysis,FDA),以函数曲线的形式表示离散观测值,运用函数曲线的研究方法剖析数据.FDA包括函数型主成分分析(Functional Principal Component Analysis,FPCA)[2]、主微分分析(Principal Differential Analysis ,PDA)[3]、函数型聚类分析[4]以及函数型回归分析[5]等方法.
与传统回归模型不同,函数型回归分析模型无过多假定和约束,其参数是关于时间的函数,适用性较为广泛.为提高函数型线性回归模型(Functional Linear Regression,FLR)[1]的预测能力和可解释性,众多学者对FLR做了拓展[6-10].如胡锡健等[11]针对汾渭平原的空气质量数据与气象数据,建立关于气温曲线与月均SO2浓度的函数型空间自回归模型;苏梽芳等[12]提出基于残差函数主成分的估计方法,以预测股市开盘价;Oshinubi等[13]基于FPCA分析法国COVID-19数据,并通过建立FLR模型预测死亡人数.函数型回归模型要求协变量或响应变量具有函数型变量,有以下4种情况[5]:
(1)协变量为函数型变量,响应变量为标量;
(2)协变量为向量,响应变量为函数型变量;
(3)协变量和响应变量都为函数型变量;
(4)协变量为函数型变量和标量的混合变量.
鉴于西班牙COVID-19数据的函数特性,本文考虑第三种情况.
在实际应用中,由于观测遗漏、数据记录或录入错误和设备维护等,数据缺失是常见的问题[14-15],其会不同程度地增大统计分析的复杂性和难度,降低统计推断的精度,最终导致统计分析结果偏误.例如在创新药开发临床试验中,因受试者失访、对干预措施不耐受或缺乏疗效等原因中途退出试验等导致数据缺失,严重影响临床试验结果[16].因此,如何准确插补医学数据中的缺失数据具有重要意义.在处理缺失数据时,通常采用删除法、多重插补法和回归插补法等[17].回归插补法是最常见且有效的方法,其利用变量间的关系进行插补,使得模型更具解释性.例如惠娇娇[18]构建了函数型线性空间自回归模型和函数型线性空间误差模型,并将其应用于西班牙气象数据,结果表明所提两种模型效果均优于FLR;Acal等[19]基于西班牙COVID-19数据,提出多元函数型主成分回归模型,插补住院人数和ICU人数.
本文针对随机缺失机制[20]下函数型响应变量缺失的数据,结合FPCA和PDA的思想,构建基于函数型主微分与主成分的岭回归模型(Ridge Regression Model based on Functional Principal Differential and Principal Component,FPDPCRR).该方法同时考虑原始数据曲线信息和曲线波动特征信息两个视角,将两视角的估计聚合为最终预测结果,解决函数型响应变量存在缺失的插补问题.以西班牙COVID-19数据为例,验证FPDPCRR模型的估算能力,具有较好的实际应用效果.同时,典型相关分析呈现入院率与疾病反应之间存在高度相关关系,进一步说明该模型自变量和响应变量选取的合理性.
1 相关理论基础
1.1 离散数据的曲线拟合
在离散时间点{tj}观察一个连续可微的过程,
yj=x(tj)+εj,
(1)
其中:{yj}为观测值;x(t)为连续可微的拟合函数;εj为误差成分.通常使用最小二乘准则刻画x(t)的准确性;另外,采用粗糙惩罚法保证x(t)的匀滑程度.曲线拟合方程为
(2)
其中:Dk为k阶导数;λ为修匀参数,可由广义交叉验证准则得到.一般地,最小化式(2)可得到x(t).
1.2 多元函数型主成分回归模型
多元函数型线性回归模型是利用J个函数型预测变量X=(X1,…,XJ)′来估计函数型响应Y.具体模型为
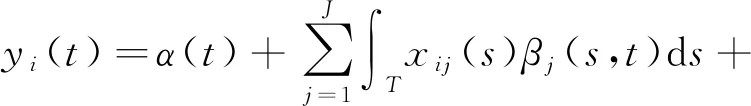
(3)
其中:α(t)为截距函数;βj(s,t)为J个系数函数;εi(t)是独立的误差函数.
由于多元函数型线性回归模型易受多重共线性的影响,导致参数估计精度下降.因此,Acal[19]提出了多元函数型主成分回归模型(Multivariate Functional Principal Component Regression Model,MFPCR).
函数型预测因子和函数型响应的主成分分解分别为
(4)
其中,权重函数fl(t)是样本协方差算子的特征函数,ξil(t)为主成分得分.由式(3)和式(4)得

(5)
通过截断每个主成分分解,得MFPCR模型为
(6)
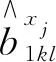
1.3 主微分分析
主微分分析是通过微分方程来拟合噪声数据,以捕获单个曲线特征或曲线的变化特征.假设对于t∈R,函数型数据x(t)有如下线性微分算子L:
Lx(t)=β0(t)x(t)+…+
βm-1(t)Dm-1x(t)+Dmx(t)=f(t),
其中:βj(t)为权重函数;f(t)为强迫函数.
由逐点最小化法[21],得β(t)的最小二乘解为
(7)
其中,Z(t)为N×m阶矩阵,其第i行为Zi(t)={-xi(t),…,-Dm-1xi(t),fi(t)}.
2 基于函数型主微分与主成分的岭回归模型
考虑到函数型主成分代表函数曲线的绝大部分信息,而主微分旨在刻画函数曲线的主要变化特征,如曲线的变化趋势、梯度以及曲率等特征.同时考虑主微分与主成分两个视角,将有助于提高函数型回归模型的预测精度.因此,构建FPDPCRR模型,从两个互补视角中估计预测值,并自加权的调节视角权重,获得最终预测结果.
类似于FPCA中主成分得分,定义xi(k)的第k个PDA得分[22],
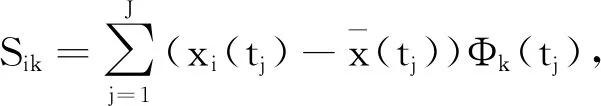
(8)

函数型预测因子和函数型响应的主微分分解为
(9)
结合式(3)和式(9),有
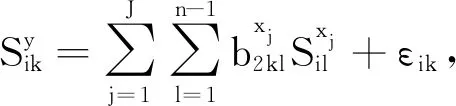
(10)
受MFPCR模型[19]启发,引入PDA结果,整合两个视角的估计值,FPDPCRR模型为
(11)
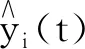
其中:γ是正则化参数,l2是正则化项,有助于提高模型的泛化能力.

特别地,当ω2=0时,FPDPCRR退化为MFPCR模型;而当ω1=0时,FPDPCRR退化为多元函数型主微分回归模型(Multivariate Functional Principal Differential Regression Model,MFPDR):
然而,由于MFPCR模型仅考虑函数曲线的绝大多数信息,而MFPDR模型仅考虑函数曲线波动信息,理论上它们的预测插补性能次于FPDPCRR模型.为此,下面运用实例来证明上述推断.
3 实例检验
3.1 数据说明
本文以西班牙17个地区的COVID-19数据为例,运用所提FPDPCRR方法对其进行预测插补.17个地区包括:安达卢西亚、阿拉贡、阿斯图里亚斯、巴利阿里群岛、加那利群岛、坎塔布里亚、卡斯蒂利亚拉曼查、卡斯蒂利亚莱昂、加泰罗尼亚、埃斯特雷马杜拉、加利西亚、马德里、穆尔西亚、纳瓦拉、派斯瓦斯科、拉里奥哈和巴伦西亚.为描述方便起见依次记为:AC1-AC17.进一步,为验证FPDPCRR模型中自变量和响应变量选择的合理性,对插补后的完整数据进行典型相关分析.
3.2 曲线拟合
首先,对确诊人数、死亡人数、康复人数、住院人数和ICU人数5个变量进行曲线拟合并修匀,分别表示为X1(t),X2(t),X3(t),Y1(t)和Y2(t).本文选用 4阶B-样条基函数拟合函数曲线.修匀参数λ=1e-3.分别绘制上述变量的拟合曲线,如图1所示.
3.3 FPDPCRR模型应用
基于FPDPCRR模型处理Y1(t)和Y2(t)的缺失插补预测问题.具体地,首先运用13个具有完整数据的地区估计FPDPCRR模型;其次对4个缺失地区的数据进行插补预测.
估计5个函数型变量的每个函数型主成分,结果表明第一个主成分解释了5个变量中的绝大部分信息,即X1(t),X2(t),X3(t),Y1(t)和Y2(t)分别为99.2%、98.3%、97.9%、91.9%、93.9%.
在得到5个变量的函数型主成分之后,基于PDA思想,选取二阶微分方程分别对X1(t),X2(t),X3(t),Y1(t),Y2(t)进行PDA,并利用式(8)计算得到各变量的两个主微分得分.然后,将13个完整数据的地区看作预测样本,分别考虑预测变量和响应变量之间主微分得分、第一主成分的相关性.因此,根据每个预测变量的主微分得分和第一主成分,将函数型线性回归模型简化为主微分回归模型:
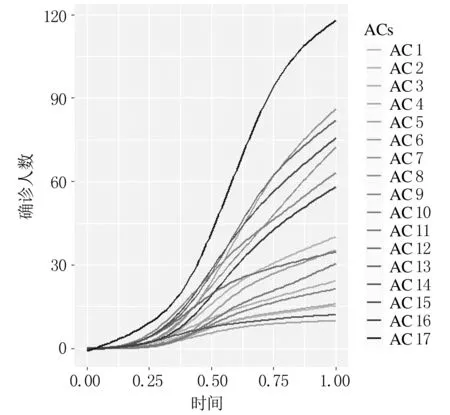
(a) X1(t)

(b) X2(t)

(c) X3(t)

(d) Y1(t)
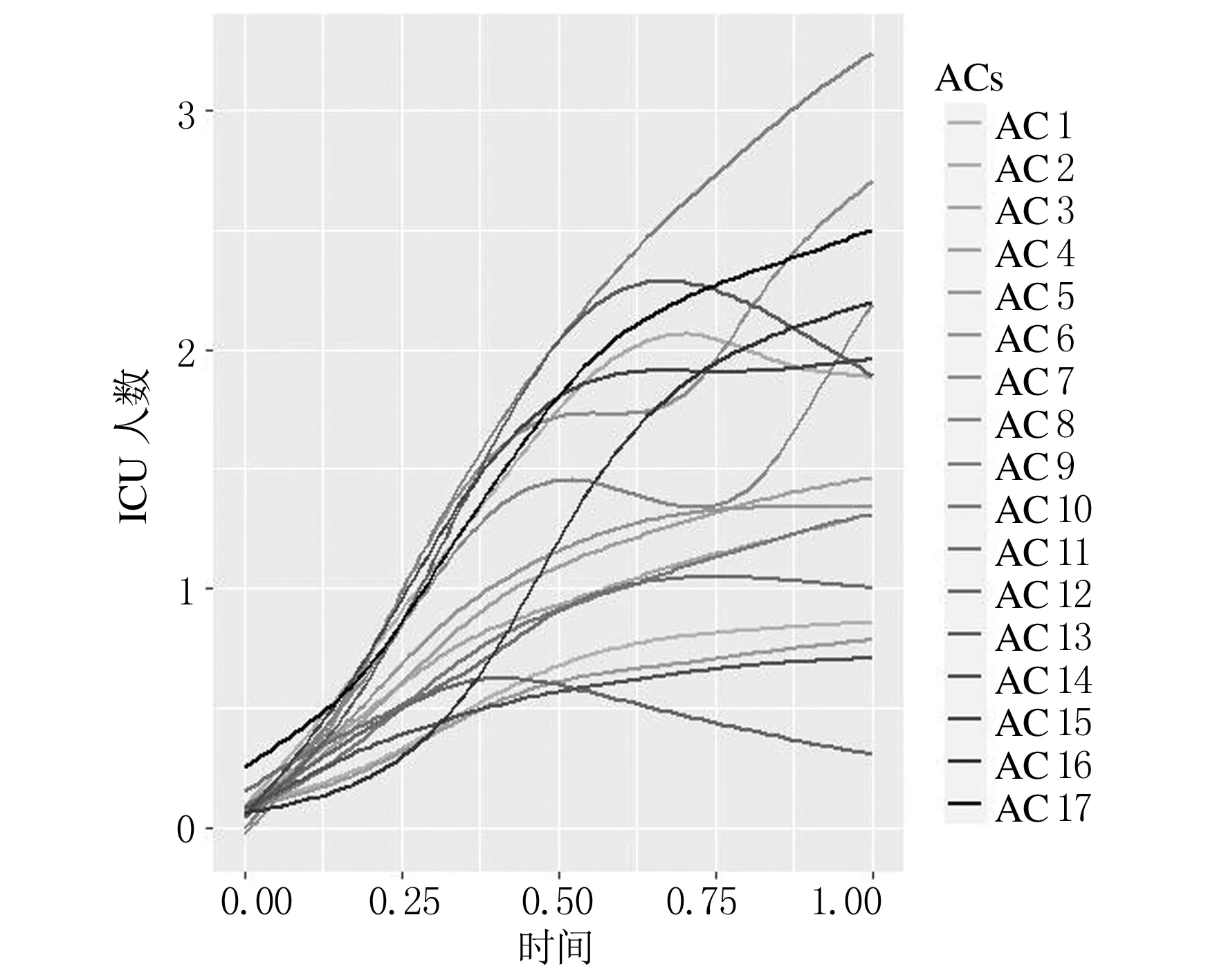
(e) Y2(t)图1 5个函数型变量拟合曲线图
以及第一主成分回归模型
其中k=1,2;i=1,…,17;j=1,2.上述模型可以基于X1(t)、X2(t)和X3(t)的主微分得分和第一主成分分别准确估计Y1(t)和Y2(t)的主微分得分和第一主成分,其决定系数如表1所列.显然,第二主微分得分的解释性优于第一主微分得分.因此,选取第二主微分得分和第一主成分进行函数型数据插补.

表1 X1(t),X2(t),X3(t)分别与Y1(t),Y2(t)的决定系数
(12)
为展示所提FPDPCRR模型的插补预测效果,采用均方根误差(RMSE)、归一化均方根误差(NRMSE)以及均方根百分比误差(RMSPE)作为评估指标.具体公式为
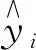
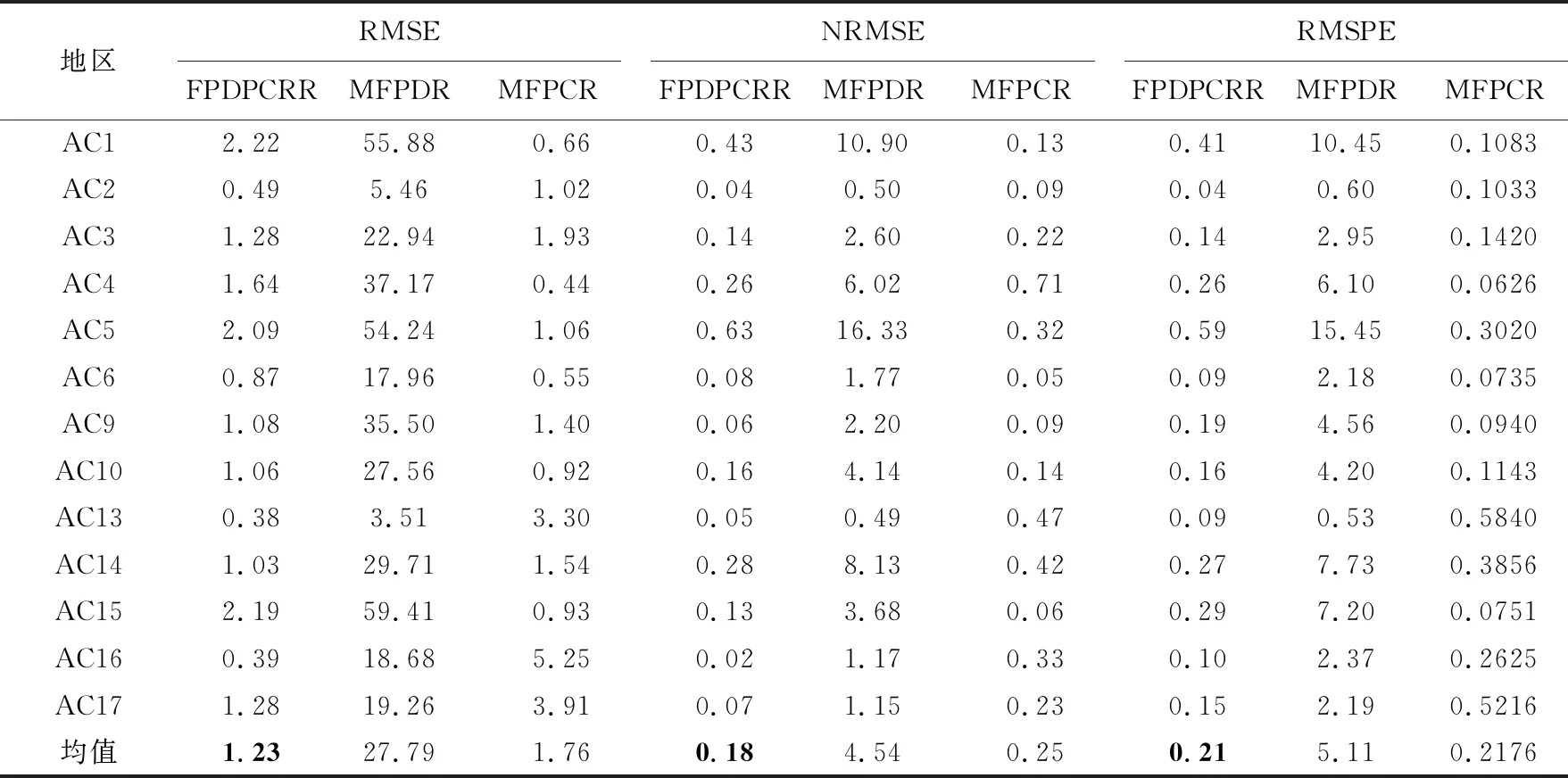
表2 住院人数曲线的预测效果评估对比
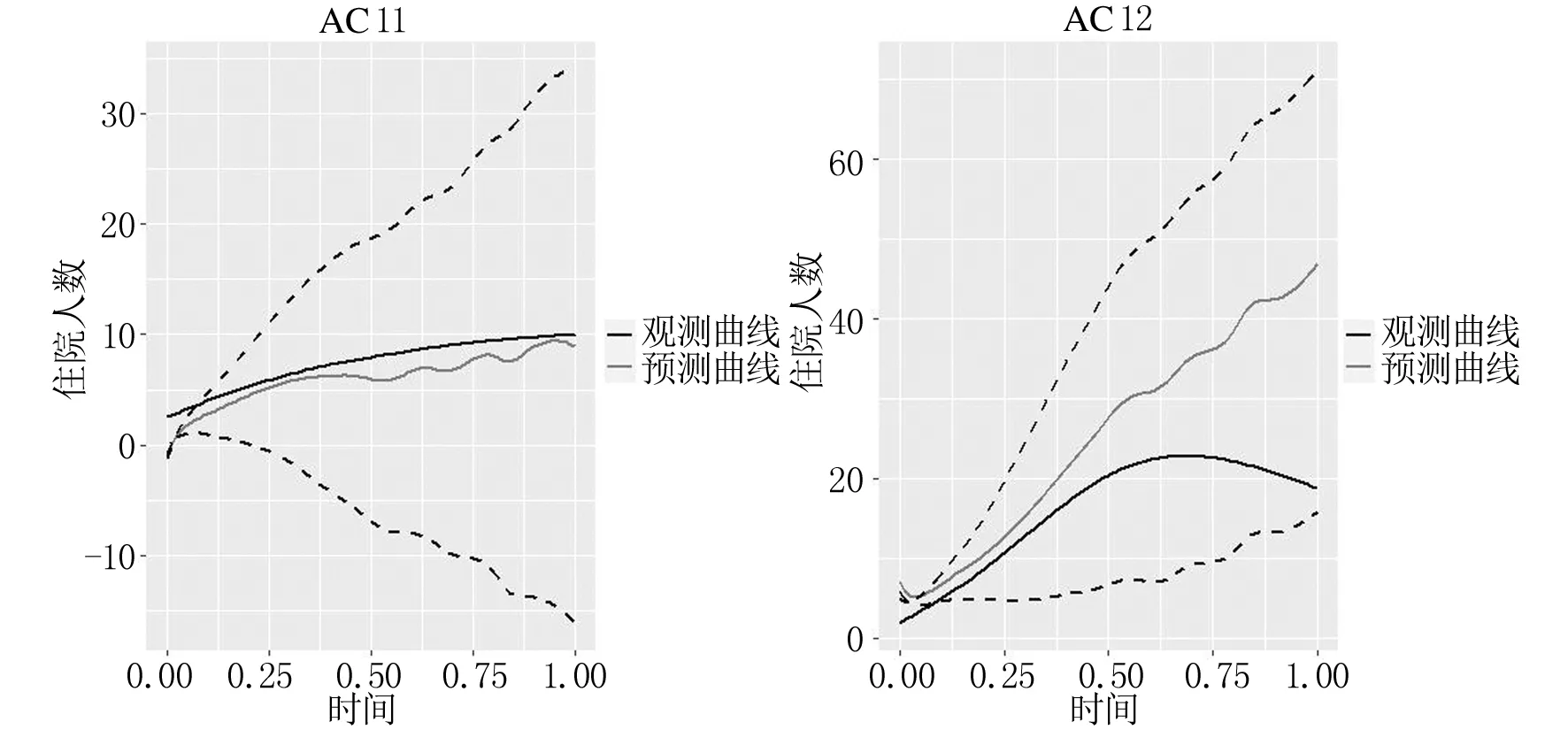
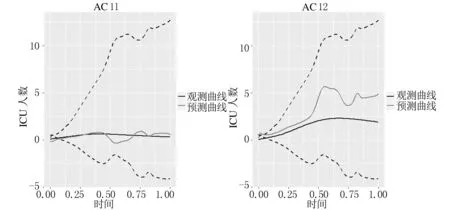
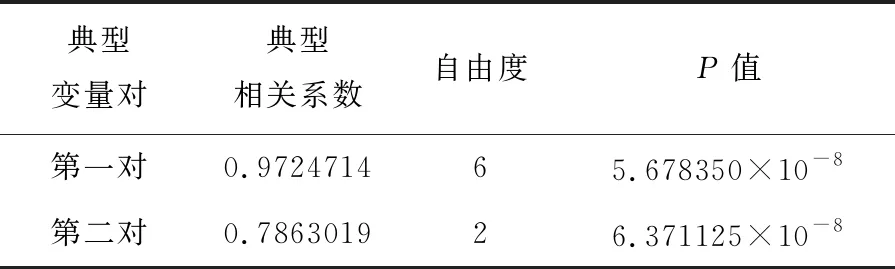
由表2、表3可知,MFPDR模型的三个评估指标均大于FPDPCRR模型和MFPCR模型,表明其插补预测能力较差.个别地区的MFPCR模型的预测效果略优于FPDPCRR模型的,但从平均结果来看,FPDPCRR模型三个评估指标的均值均小于MFPCR模型,其预测效果优于MFPCR模型.这意味着引入主微分,从数据曲线及其波动特征信息两个互补视角中估计,可进一步提升预测性能.总的来说,三个模型的插补预测性能:MFPDR模型 此外,分别绘制由FPDPCRR模型插补预测的4个数据缺失地区 (AC7、AC8、AC11和AC12)的住院人数和ICU人数的预测曲线、观测曲线以及其置信区间,分别如图2、图3所示,图中黑色实线表示观测曲线,灰色实线表示预测曲线,黑色虚线表示置信带. 图2 住院人数的观测曲线、预测曲线及置信区间 图3 ICU人数的观测曲线、预测曲线及置信区间 为进一步说明所提FPDPCRR模型的插补预测精度,以及模型变量选择的科学性,下面基于典型相关分析研究入院人数与受疾病影响人数之间的关系.由于函数型变量的主微分之间、主成分之间的相关性较高,则变量非线性独立.在不区分自变量和因变量的情况下,将典型相关分析应用于这些函数型变量的主成分与主微分加权的得分中,以解释两组变量之间的相关关系. 表4 典型相关系数及显著性结果 两组变量的标准化典型相关系数,其大小表示各变量对相应典型变量的贡献,如表5,表6所列.典型变量为 U1=0.08019246×ξy1+0.2844273×ξy2, 0.71636136×ξx2+0.02283154×ξx3, (a) 第一对典型相关变量 (b) 第二对典型相关变量图4 典型相关变量的散点图 表5 HOR的标准化典型系数 表6 IR的标准化典型系数 HOR、IR变量与典型变量之间的平方相关性如表7和表8所列.第二典型变量对(U2,V2)的相关性较小;而第一典型变量对(U1,V1)与除康复人数之外的其他变量的相关性均较高,表明U1与住院人数和ICU人数更相关,V1与确诊人数和死亡人数更相关. 表7 HOR变量和典型变量之间的平方相关性 表8 IR变量和典型变量之间的平方相关性 上述结果表明,医院的入院率特别取决于住院人数;同时,对于大流行病的应对能力主要取决于确诊人数和死亡人数.尽管ICU人数和康复人数在典型变量中起着重要作用,但其贡献较小. 最后进行典型冗余分析,以研究典型变量对于各变量的信息提取量情况,分析结果如表9所列.可以看出,第一典型变量对(U1,V1)提取了原始变量的大多信息,HOR和IR组的解释方差比例分别为0.909和0.618,而第二典型变量对几乎没有贡献. 表9 方差解释率 本文考虑FPCA能够代表原始数据的绝大多信息,PDA既能反映曲线的变化趋势,又能挖掘数据的梯度、曲率等潜在信息,从这两个视角出发,针对响应变量存在缺失的函数型数据,构建FPDPCRR模型,并利用西班牙COVID-19数据评估该模型.结果证实,与MFPDR模型和MFPCR模型相比,所提FPDPCRR模型插补预测效果最优.最后,为验证模型中变量的选取问题,基于插补预测的完整数据,运用典型相关分析解释HOR与IR之间的相关关系,结果表明两组变量彼此高度相关,住院人数对HOR的影响较大,确诊人数和死亡人数对IR的影响较大,ICU人数和康复人数在典型变量中的贡献较小.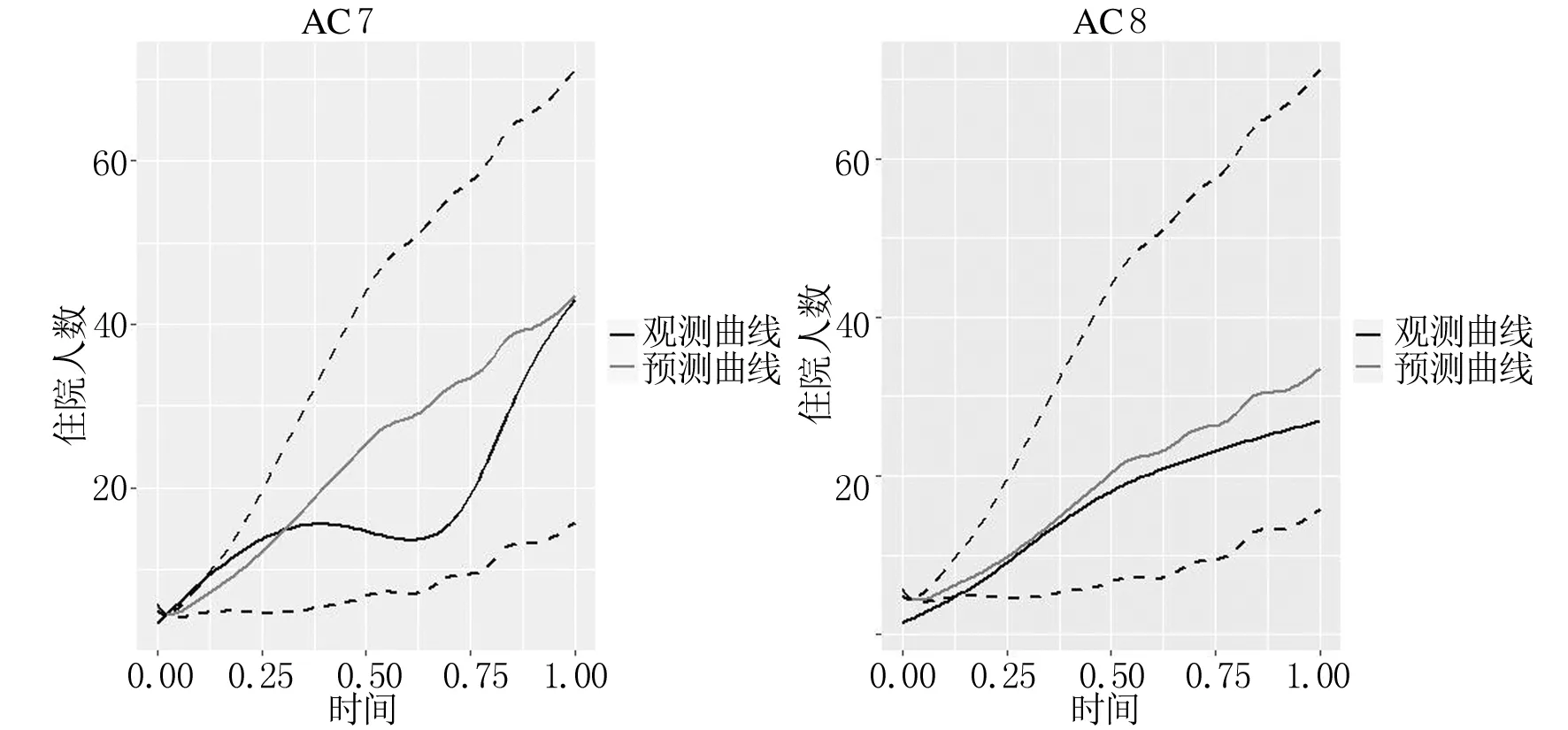
3.4 典型相关分析

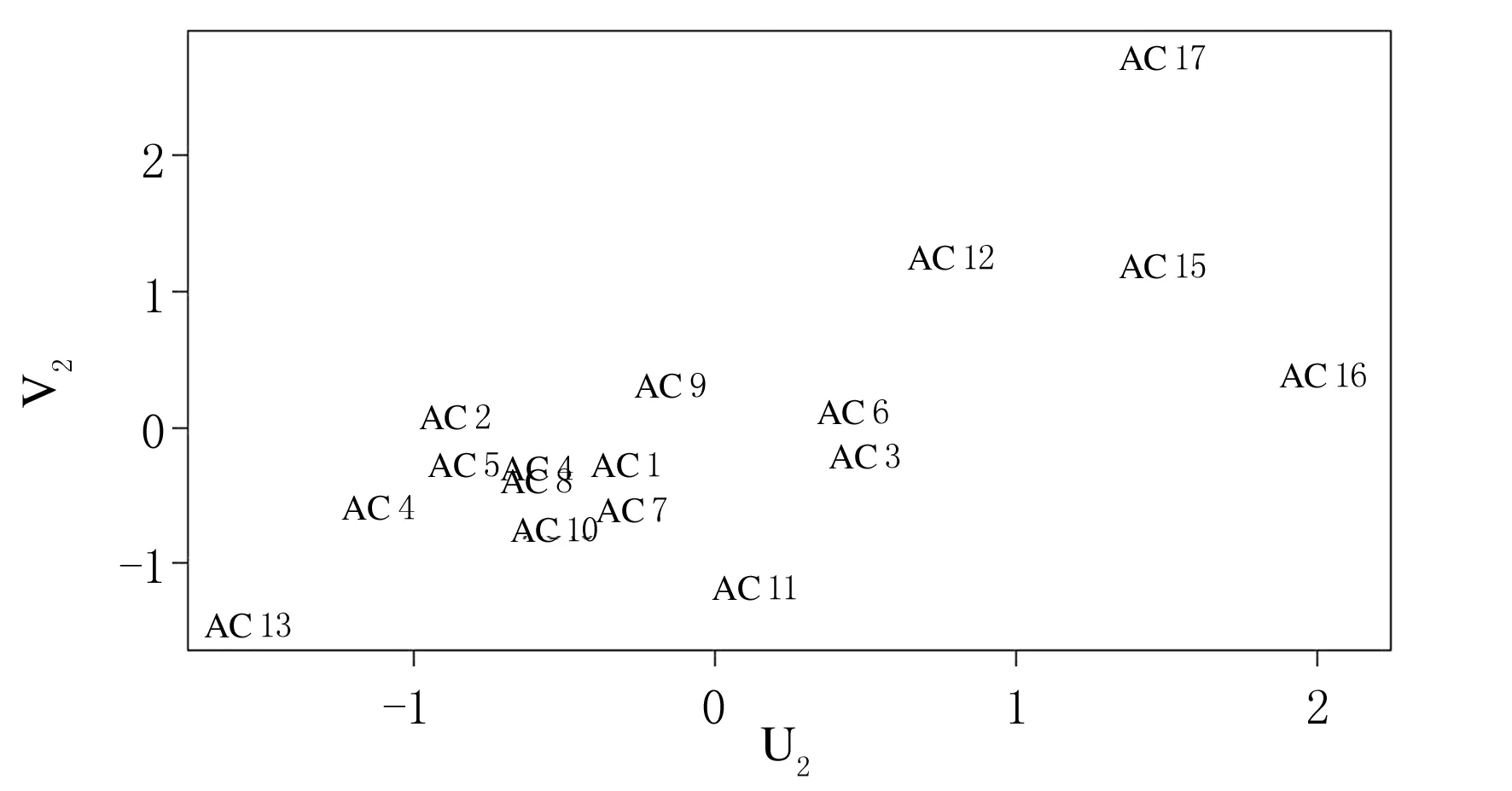
U2=-2.2768425×ξy1+0.3162396×ξy2,
V1=-0.01284091×ξx1+
V2=-0.14690342×ξx1-
1.12059582×ξx2-0.08767666×ξx3.





4 结语
