基于RBF 神经网络的新型AUV 自抗扰控制方法

乌云嘎，徐会希，姜志斌

(1.中国科学院沈阳自动化研究所机器人学国家重点实验室，辽宁 沈阳 110016；2.中国科学院机器人与智能制造创新研究院，辽宁 沈阳 110169；3.辽宁省水下机器人重点实验室，辽宁 沈阳 110169；4.中国科学院大学，北京 100049)

0 引 言

AUV 因其自主、智能的特性，在水下环境探测和资源勘探方面发挥了人工无法比拟的作用[1]。AUV 作业过程中，受到海浪和水流的干扰，所以在近海底自主观测、轨迹跟踪等要求精细控制的场景，必须考虑外界环境扰动对AUV 稳定性的影响。AUV 平台具有多变量、非线性、强耦合、外界干扰多和内部参数时变的特点，要想达到理想的控制效果，往往需要收敛速度快、抗干扰、鲁棒能力强的控制器，这些要求给控制系统的设计带来了很多困难。

基于对象信息的现代控制理论包含对模型不确定性的近似，这种近似性使得AUV 控制系统性能有待提高。针对控制器本身存在不足及其对扰动抑制能力弱的问题，韩京清等[3–5]提出了一种抗扰动控制方法，对控制模型信息依赖少，具有天然的解耦性和优秀的抗干扰能力，被广泛应用于机器人控制。针对非线性自抗扰控制参数比较多的问题，高志强[6]提出了线性化版本，简化了工程实现和参数整定，更加便于工业推广。

目前针对线性自抗扰控制器的理论研究主要集中在其时域和频域特性的探索，以及与PID 的关系的证明上，总结出了很多控制器调参的指导方法。其中，JIN 等[7]证明二阶线性ADRC 可以等效于增加了前馈和二阶低通滤波器PID 控制，并提出了按照等效PID 参数对二阶线性ADRC 调参的方法。崔文庆等[8]说明在中低频段线性ADRC 等效于PID 控制器串联n阶超前环节。除了根据频域特性和类比PID 的调参方法，还有很多自适应调参方法，如基于强化学习改进的自抗扰控制算法在无人船中的应用[9-10]。以上理论分析说明ADRC 实际上是改进版的PID，PID 是ADRC 的一种特殊情况。但是当输入阶跃信号的幅值改变较大时，得到的过渡过程不同，原有的扩张状态观测器对扰动的观测误差将增大，进而影响系统的稳定性，需要重新调节控制器参数，才能取得好的控制效果。

为此，本文提出一种基于RBF 神经网络补偿的线性自抗扰控制方法：利用神经网络的自学习和自适应能力，将其用于扰动观测器的改进，实现在不同阶跃信号下对扰动的准确估计，以此改善ADRC 的控制性能，简化控制器调参过程，提高控制器的鲁棒性。将改进后的控制器应用于AUV 的航向角控制，通过仿真实验说明了方法的有效性，验证了所提方法对不同采样频率的鲁棒性。仿真结果表明，在低采样频率下改进后的控制方法有更好的控制效果，对实际工程具有参考意义。

1 AUV 模型

1.1 坐标系、术语和符号定义

按照国际水池（ITTC）推荐的和造船与轮机工程学会（SNAME）术语公报的体系[11]，采用2 个右手坐标系表述AUV 的运动学和动力学模型：一个是固定于地球上的定坐标系E-ξηζ，原点取为水中任意一点；另一个是与AUV 固联并随之运动的动坐标系G-xyz，原点取为AUV 的浮心。AUV 的位置和姿态分别用动系相对于定系的坐标（ ξB， ηB， ζB）和姿态角（横滚角 φ，纵倾角θ，航向角 ψ）表示，而AUV 运动的速度（u，v，w）、角速度（p，q，r）、所受力（X，Y，Z）和力矩（K，M，N）定义于动坐标系中，规定向量正方向沿对应坐标系正方向，所有旋转变量采用右手螺旋规则确定方向。坐标系和变量的定义如图1 所示，各变量对应的符号列于表1。

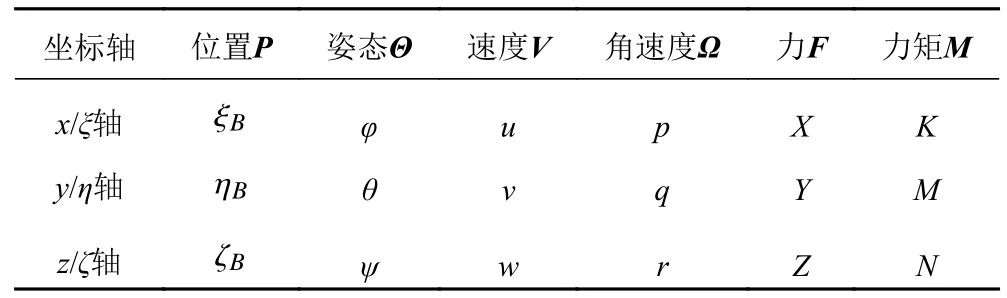
表1 变量对应的符号Tab.1 Signs of parameters

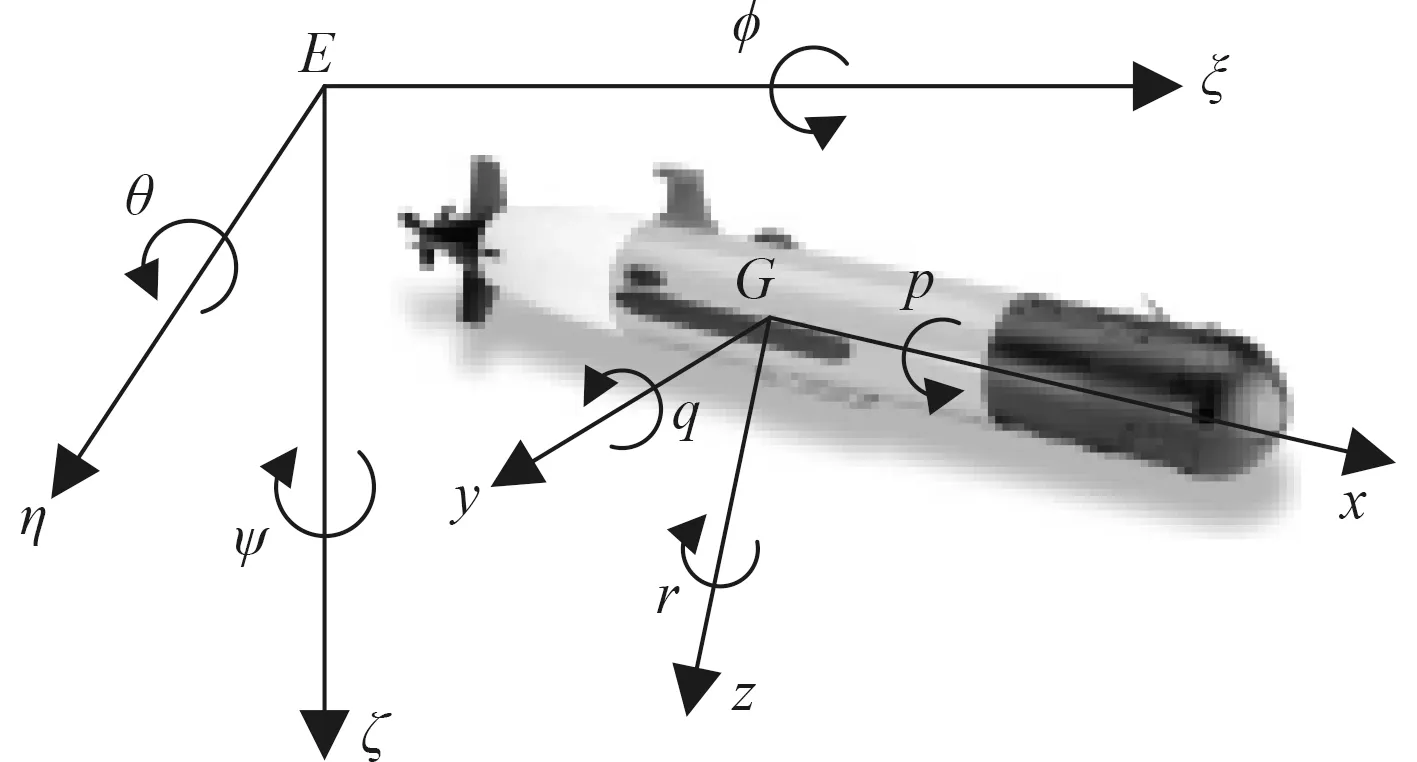
图1 坐标系和变量示意Fig.1 Coordinate systems and parameters

1.2 AUV 运动学模型

将AUV 看做自由运动的刚体，根据刚体六自由度运动学方程，AUV 位姿和运动速度之间的转换关系表达为：

式中：T表示速度矢量从动系到定系的变换矩阵，R代表角速度矢量从动系到定系的变换矩阵。

1.3 AUV 动力学模型

将AUV 看做刚体，参考刚体动力学公式推导AUV 动力学模型。记v=[VΩ]T，根据刚体六自由度动力学方程：

式中：MRB∈ℜ6×6为 惯性矩阵；CRB∈ℜ6×6为科氏力和向心力矩阵； τRB∈ℜ6为刚体受到的所有外力和外力矩。对于水下航行器应用环境，表达式[12]为：

式 中： τhyd=-MAv˙r-CA(vr)vr-D(vr)vr为 水 动 力 项，τhs=-g(Θ)-g0为重力、浮力和载重产生的水静力项，τdis表示来自水流、海浪等的环境干扰力、力矩，τ=为推进器和桨、舵的操纵力。本文实验使用的模型为REMUS 100 AUV，其操纵力来自尾推进器、垂直操纵舵和水平操纵舵。

1.4 AUV 航向角控制模型

由式（2）和式（3）得到AUV 状态变量的加速度表达式为：

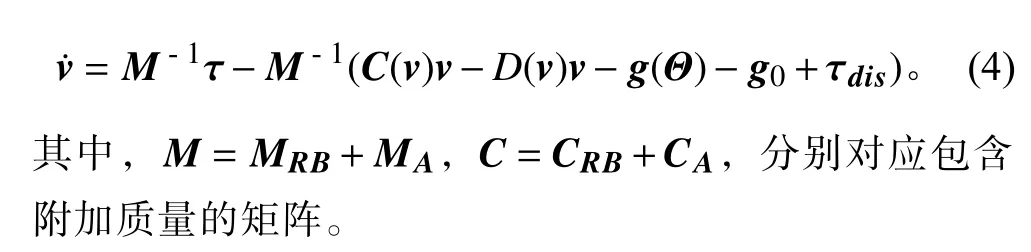
实际控制器按照解耦后的模型来设计，所以可以对模型进行合理的简化。假设整个过程中推进器的转速保持不变，AUV 处于巡航状态，当控制航向角时，只有垂直舵动作，水平舵微调用于保持纵倾角稳定。基于上述假设，得到航向角控制模型：

2 RBF 神经网络改进的自抗扰控制器

2.1 自抗扰控制技术

ADRC 将积分器串联型作为标准型，将总扰动扩张为系统的一个状态，并经观测器估计后补偿到控制输入中加以消除，达到简化控制系统、提高控制抗干扰性的目的。

ADRC 由扩张状态观测器（Extended State Observer，ESO）、跟踪微分器（Tracking Differentiator，TD）和状态误差反馈控制律（State Error Feedback，SEF）组成，如图2 所示。其中ESO 用于估计系统的状态和总扰动，生成补偿量，TD 用于配置过渡过程和获取微分信号，SEF 用于生成控制信号。

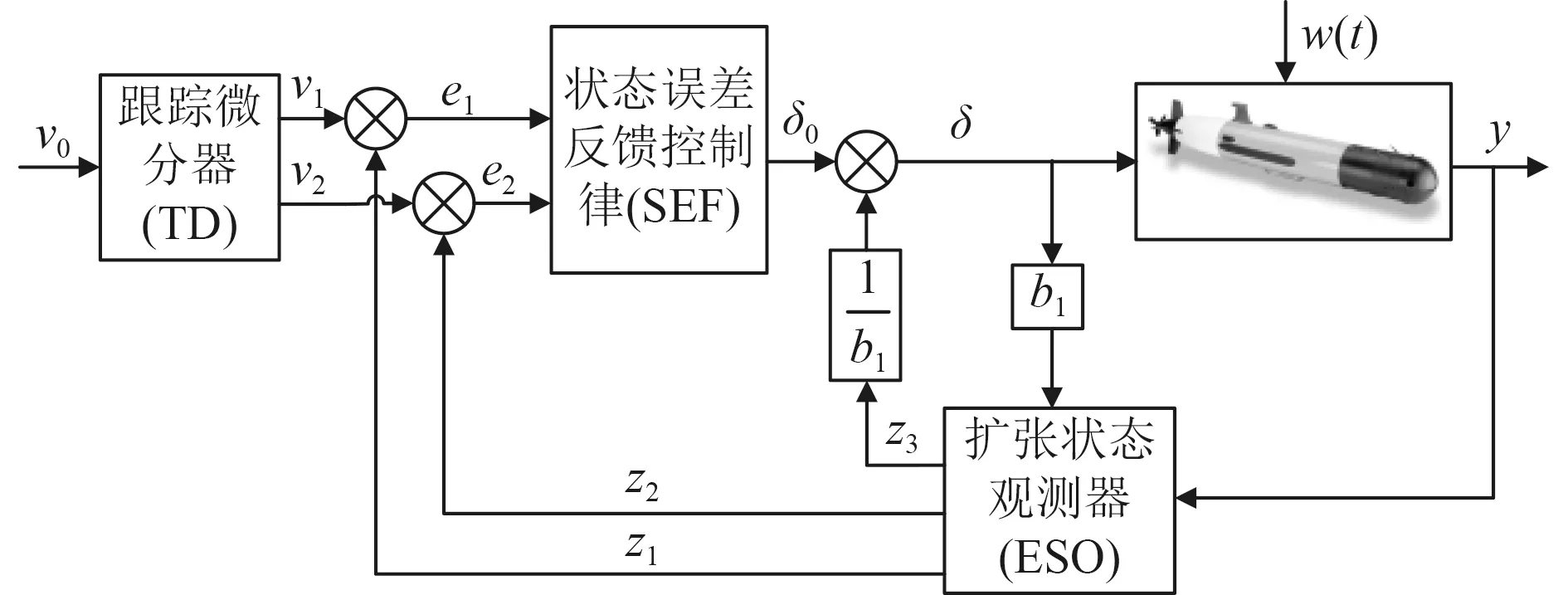
图2 ADRC 控制器结构Fig.2 Structure of ADRC controller

设二阶对象：

式中：w为外部扰动，f(y,y˙,w,t)为包含内扰和外扰的总扰动。取系统状态变量：v1=y，v2=y˙，可将上式转化为状态方程：

将航向角控制模型除控制量一阶项外的部分视为该通道的内部扰动，则式（5）变为：

对比式（6），可对航向角控制应用扩张状态观测器，估计总扰动并补偿到控制信号中。

2.1.1 跟踪微分器

TD 的算法为：

其中fhan(x1,x2,r0,h0)为最速综合函数，表达式为：

式中：r0，h0为 函数控制参量，r0称为速度因子，根据过渡过程快慢的需要和系统的承受能力决定，h0称为滤波因子，常取系统采样步长的若干倍。d=r0h20，a0=h0x2，x3=x1+a0。

TD 的状态变量v1能 够跟踪输入信号v0，配置过渡过程，生成快速、无超调的过渡信号，而v2作 为v0的近似微分能够跟踪输入信号的微分。

2.1.2 扩张状态观测器

ESO 是ADRC 的核心，其以控制信号δ和输出信号y为输入量，输出对系统状态和总扰动的估计。

将总扰动扩张成新的状态变量：

则可对系统式（7）建立线性扩张状态观测器：

2.2 自适应RBF 神经网络改进的自抗扰控制器

根据扩张状态观测器的表达式（13），观测器带宽是固定不变的，只对一定频率范围内的干扰估计效果比较好，如果扰动的频率范围较宽，观测效果就会降低，需要重新调整观测器带宽。同时，由于AUV模型具有非线性、耦合、时变的特点，不同阶跃输入和采样频率也会引起内部扰动的变化，影响观测器的效率。针对这一问题，可以用RBF 神经网络改进观测器，使之具有自适应特性。

RBF 神经网络是20 世纪80 年代末提出的一种神经网络，能以任意精度逼近任意连续函数，具有学习速度快、避免陷入局部最小值的特点，采用RBF 神经网络对系统式（7）中的总扰动进行自适应逼近。

RBFNN 是一种3 层的神经网络，结构如图3 所示，包括输入层、隐层和输出层，输入层到隐层之间为非线性映射，激活函数采用径向基函数：

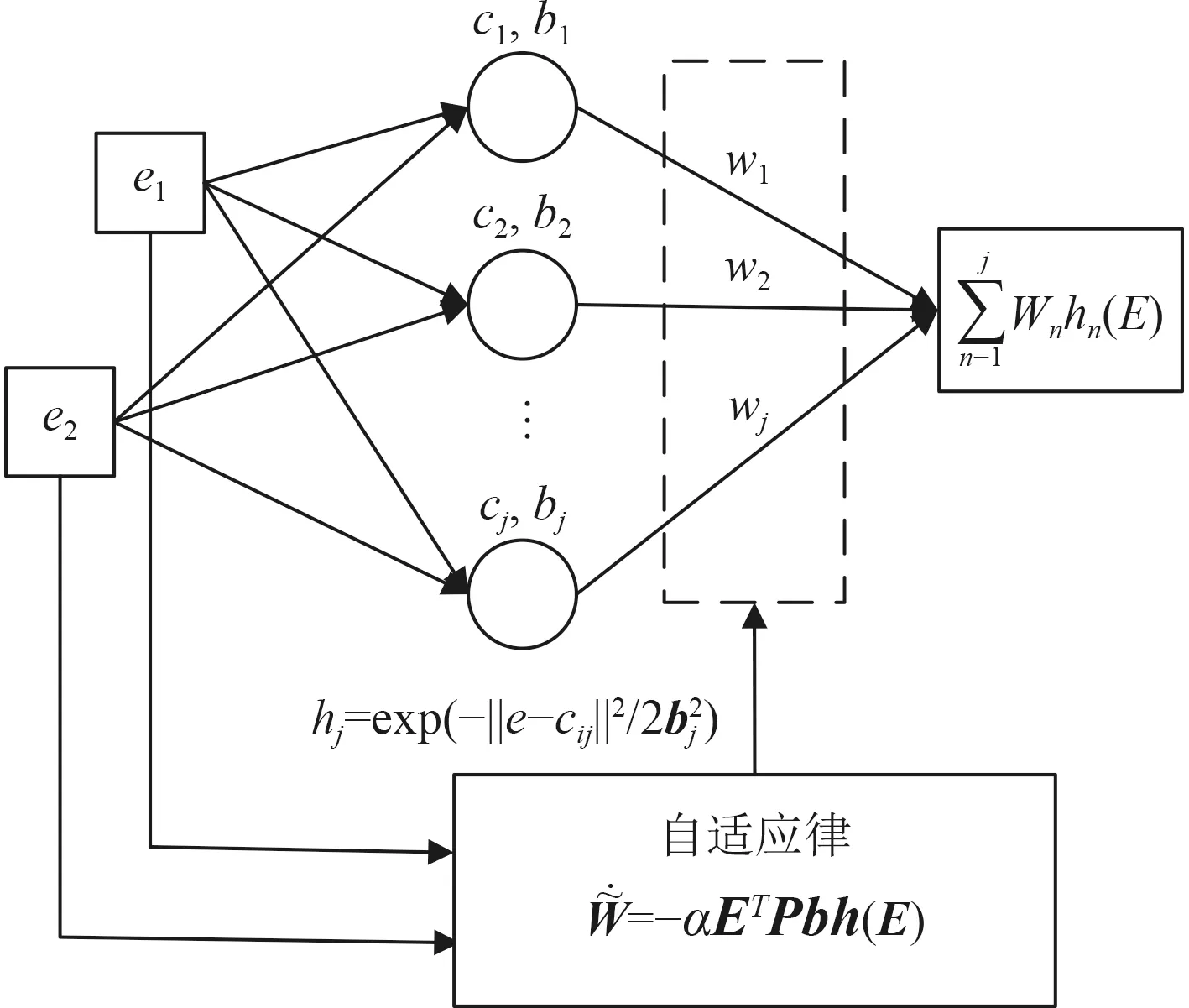
图3 RBF 神经网络结构Fig.3 Structure of RBF Neural Network

径向基函数取值仅与距中心的距离有关，且两边对称。标准的径向基函数一般取欧式距离，最常用的是高斯核函数。隐层到输出层之间为线性映射，取径向基函数输出值的加权和，权值可以通过自适应律调整，称为自适应径向基函数神经网络。

取RBF 神经网络的输入为TD 设定值和ESO 观测值的误差：

采用高斯核RBF 神经网络的算法为：

此时可使神经网络的逼近误差 σ最小，且控制系统稳定。其中， α ≥0 为神经网络的学习率，b=[0 1]T，P为一个正定矩阵，满足李雅普诺夫方程：

其中，Q是任意的 2×2正 定矩阵， Λ定义为：

式中，kp和kd对应式（16）中取值。

神经网络的实际输出为：

可以用f˜(E) 代替z3补偿控制信号，使抗扰动有自适应、自学习的性能。RBF 神经网络改进后的自抗扰控制器ADRC+RBFNN 如图4 所示。

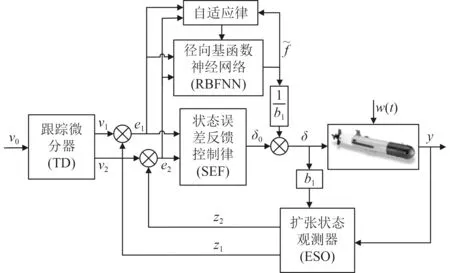
图4 基于RBFNN 改进的ADRC 控制器结构Fig.4 Structure of ADRC controller based on RBFNN

3 仿真实验

为了验证本文提出方法的有效性，设计仿真实验。针对AUV 姿态控制，分别建立PID、ADRC 和ADRC+RBFNN 控制器，进行姿态控制仿真。在不同时刻输入不同幅值的阶跃信号，对比控制器的动态响应性能；然后设计控制端扰动和反馈信号噪声，研究控制器对干扰的观测和补偿能力。最后，比较采样频率对改进前后控制器的影响，验证控制器的工程可实现性。

实验中的主要参数包括ADRC 的速度因子r0，最速综合函数步长h0，观测器带宽w0，控制器带宽wc，补偿因 子b0，PID 参数kp，Ti，Td，N，RBF 神经网 络中心矢量cij，基宽向量bj， 学习率 α。PID 控制和ADRC控制仿真参数如表2 所示。为了保证仿真结果的客观性，PID 控制的参数按照文献[8]中提出的等效PID 的参数整定，ADRC 按照文献[16]中方法得到。

表2 PID 和ADRC 控制器参数设置[2]Tab.2 Parameters setting of PID and ADRC controllers

为了得到准确的结果，仿真中改进方法的参数r0、h0、w0、wc、b0保持与ADRC 控制器参数一致。为了简化调参过程，高斯函数中心矢量cij取为零向量，基宽向量bj取 为单位向量，学习率 α =1.0。RBFNN隐含层有5 个节点，即采用2–5–1 结构。

3.1 不同阶跃输入姿态控制仿真实验

为了比较不同阶跃输入下控制器的响应性能，设计了AUV 航向角跟踪控制仿真实验。仿真时间总长150 s，分别于0 s、20 s、40 s、90 s 时输入幅值为1 0◦、-23.5◦、 3 0◦、 - 40◦的阶跃输入信号，输入幅值根据控制超调量10%得到，以便比较。

3.1.1 不含外部扰动时的仿真实验结果

仿真中采用的参数在阶跃输入为1 0◦时整定，不含外部扰动时的航向角跟踪控制仿真实验的结果如图5所示。ADRC 和ADRC+RBFNN 控制方法对v1和v2的估计误差分别如图6 和图7 所示。

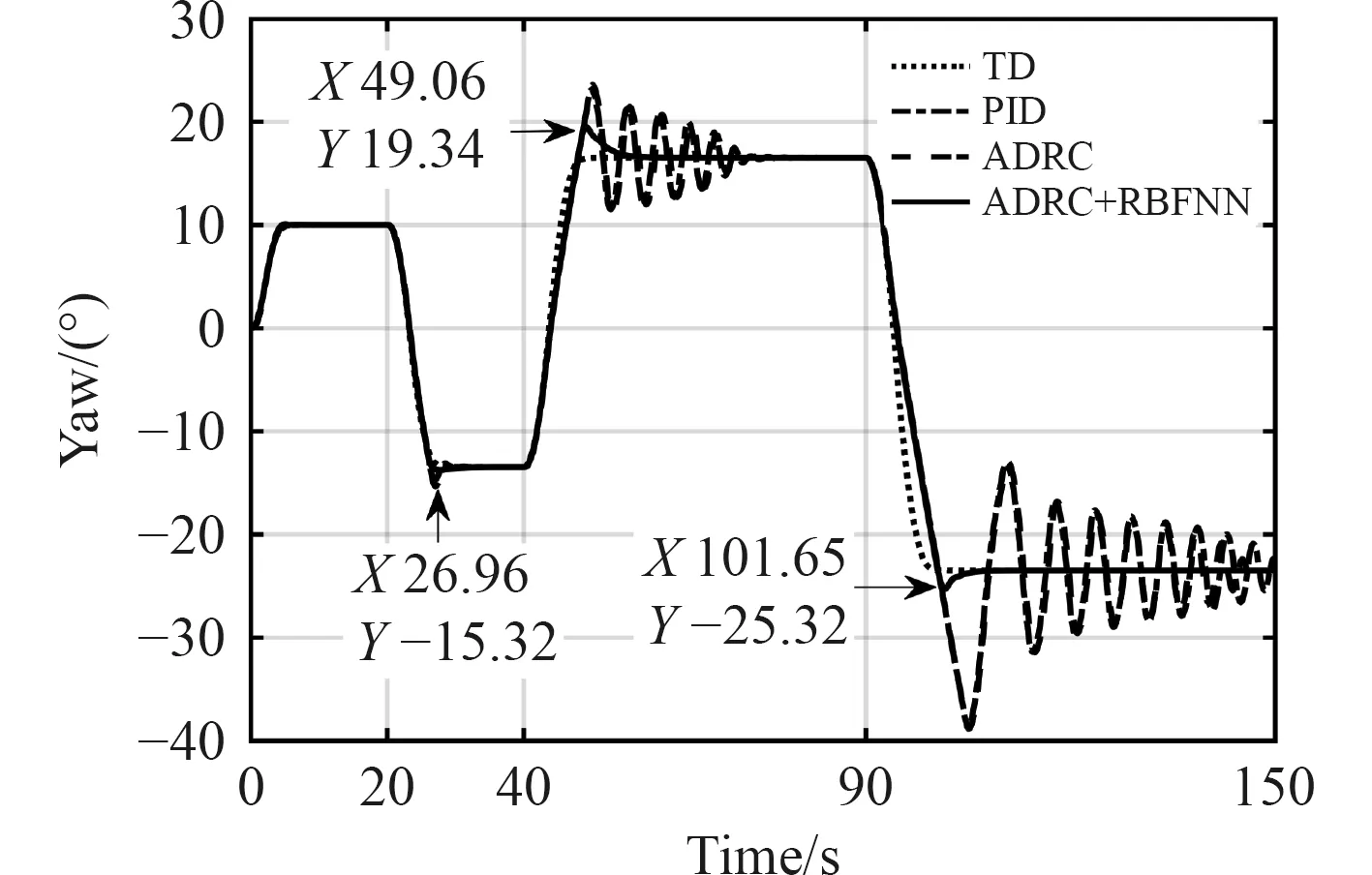
图5 无外扰时航向角跟踪控制仿真结果Fig.5 Simulation results of yaw trajectory tracking without external disturbances

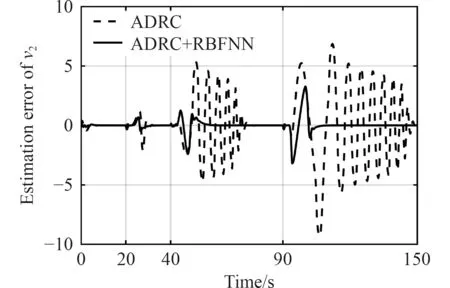
图7 不含外部扰动时 v2估计误差Fig.7 Estimation error of v2 without external disturbances

根据仿真结果可以发现，基于ADRC 的方法可以取得与PID 近似的效果，且在20 s 之前对信号的观测误差比较小，说明控制器此时可以准确的观测模型不确定部分和各通道耦合部分。

阶跃输入幅值和过渡过程的不同会影响ADRC 的控制效果，结果是当阶跃值增加到2 3.5◦时，传统ADRC控制存在13.3%的超调量，而ADRC+RBFNN 控制超调量很小，对v1和v2的 观测误差较小。当阶跃值为30◦时，改进后方法超调量为17.2%，观测误差不存在振荡，而且能够更快稳定。当阶跃值为 40◦时，改进后方法的控制效果也具有明显的优势。

仿真结果说明ADRC+RBFNN 方法在不同阶跃信号输入时，对内部扰动和系统状态估计具有自适应能力，能够保证更大范围的稳定性，简化了控制器参数整定过程。

3.1.2 含外部扰动时的仿真实验结果

根据文献[17]，外部扰动w包括控制端扰动和反馈信号噪声2 种。本次实验中控制端扰动是幅值为 6◦，周期为10 s 的正弦信号，反馈噪声是均值为 0.5◦的高斯白噪声信号。含外部扰动时的航向角根踪控制仿真实验结果如图8 所示，改进前后控制方法对v1和v2的估计误差分别如图9 和图10 所示，图11 为两者对控制端扰动的估计误差对比。

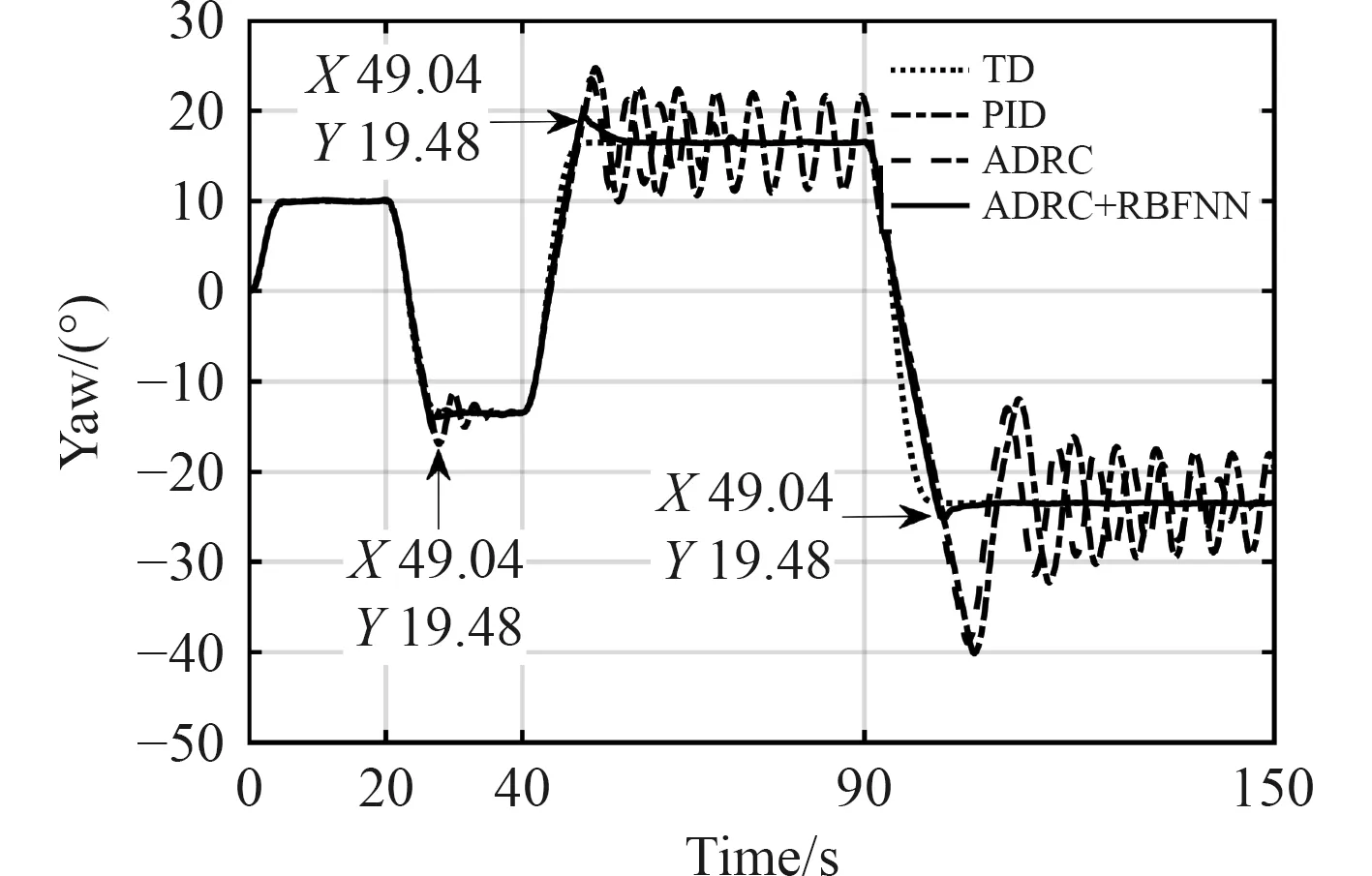
图8 含外部扰动时航向角跟踪控制仿真结果Fig.8 Simulation results of yaw trajectory tracking with external disturbances

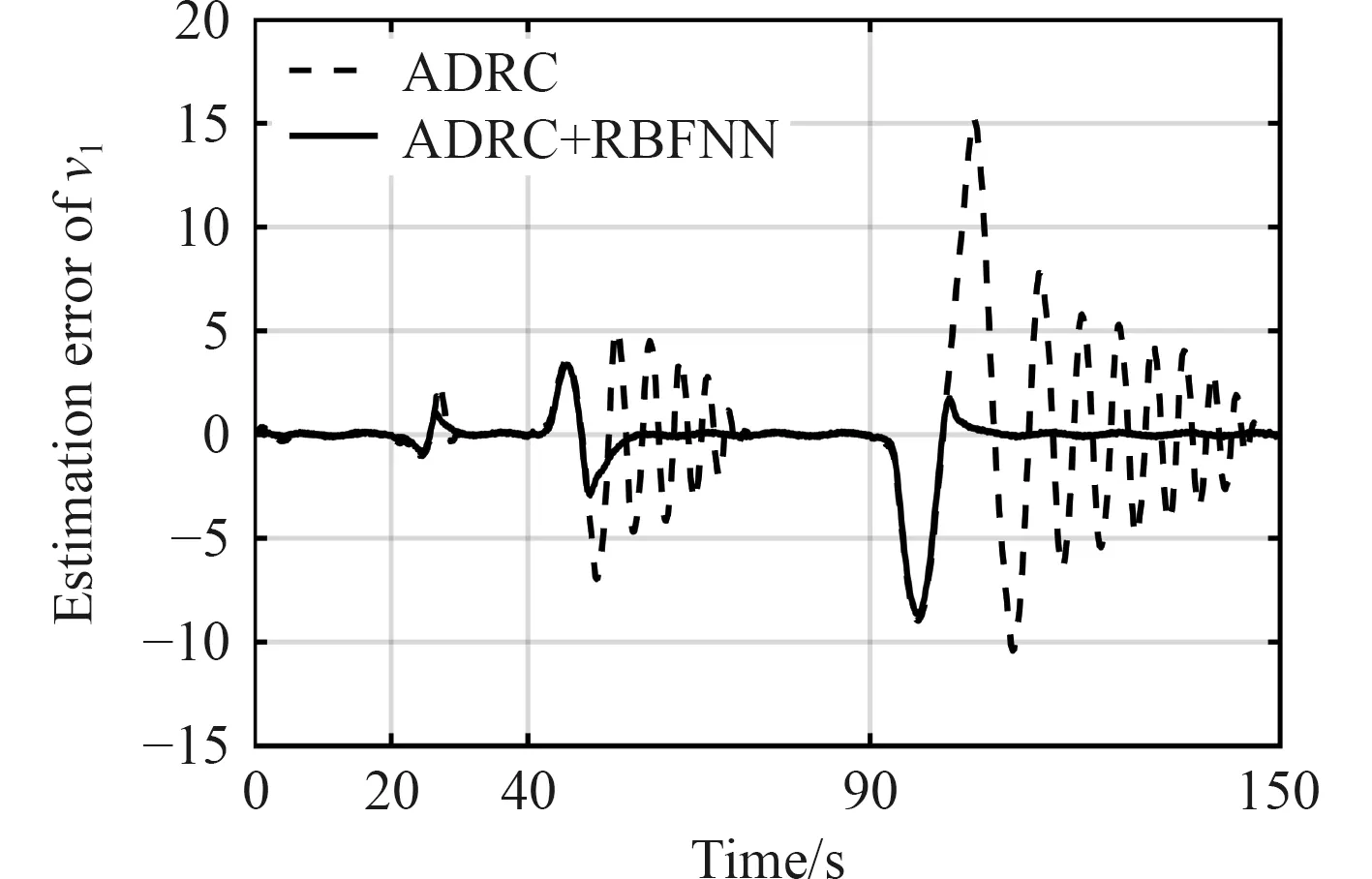
图9 含外部扰动时 v1估计误差Fig.9 Estimation error of v1 with external disturbances

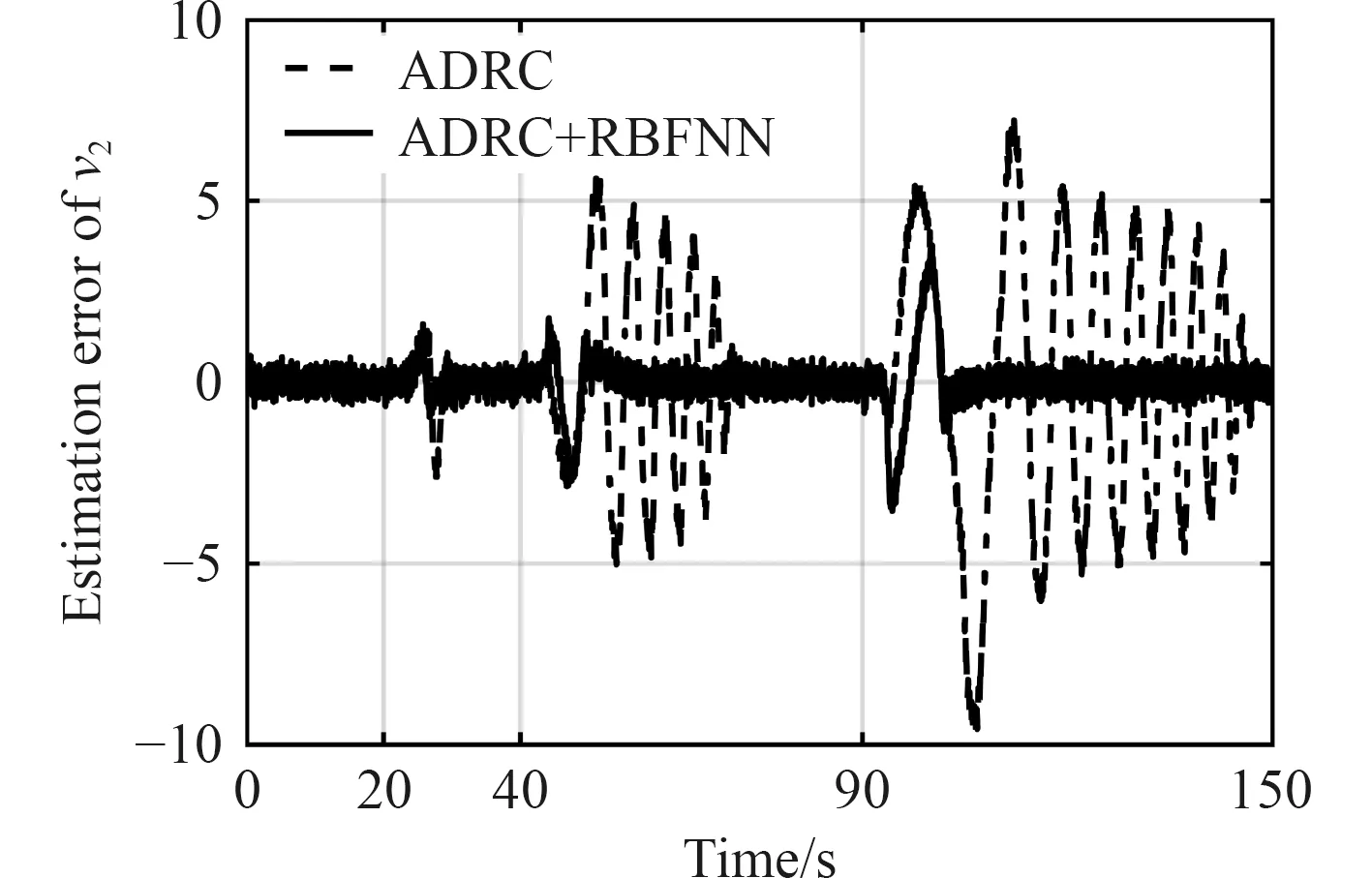
图10 含外部扰动时 v2估计误差Fig.10 Estimation error of v2 with external disturbances

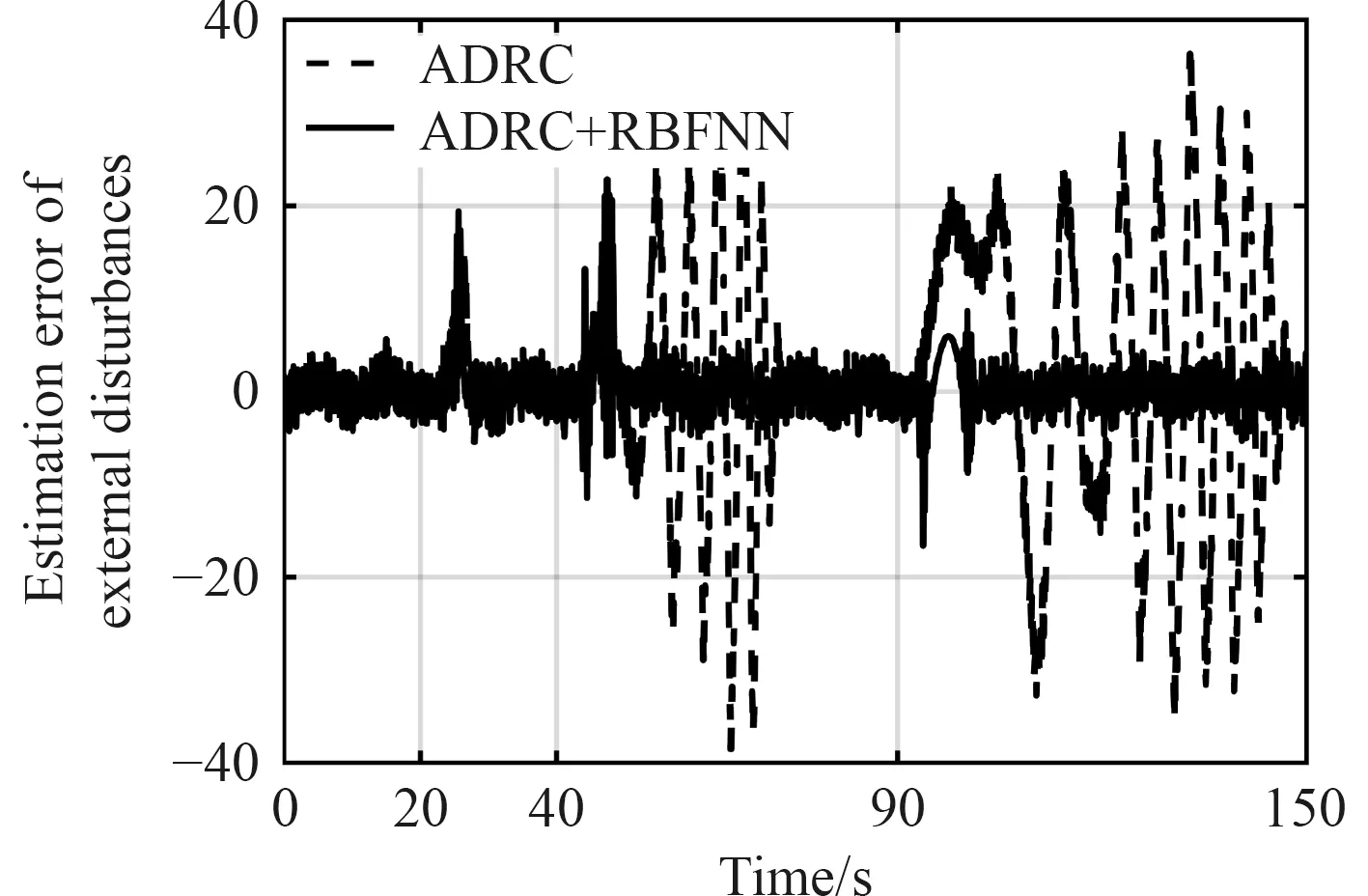
图11 航向角控制扰动估计仿真结果Fig.11 Simulation results of disturbances estimated value of controllers

由图8 可知，ADRC 控制相对PID 具有更好的抗扰动效果，可以更快稳定，但是随着阶跃值的增加，原始ADRC 控制发生一定程度的振荡。图9 和图10说明此时ADRC 对总扰动的估计出现较大误差，图11说明其对控制端扰动的估计出现较大的误差。反观ADRC+RBFNN 方法，虽然也会受到阶跃变化的影响，但是总体超调量小于原始ADRC 方法，且对扰动和状态量的估计误差能够迅速收敛。

仿真结果说明，相比ADRC 控制，本文改进方法能够更好适应不同阶跃输入的变化，对总扰动的估计更加准确，提高了控制器的稳定性和抗干扰能力。

3.2 不同采样频率姿态控制仿真实验

由于采样频率会影响扩张状态观测器的效果，而AUV 属于大惯性系统，实际平台中的采样频率比较低，有明显的离散特性。为了比较不同采样频率对改进前后控制方法的影响，设计仿真实验。选择采样频率分别为50 Hz、20 Hz、10 Hz，对比控制器的效果，仿真结果如图12 所示。

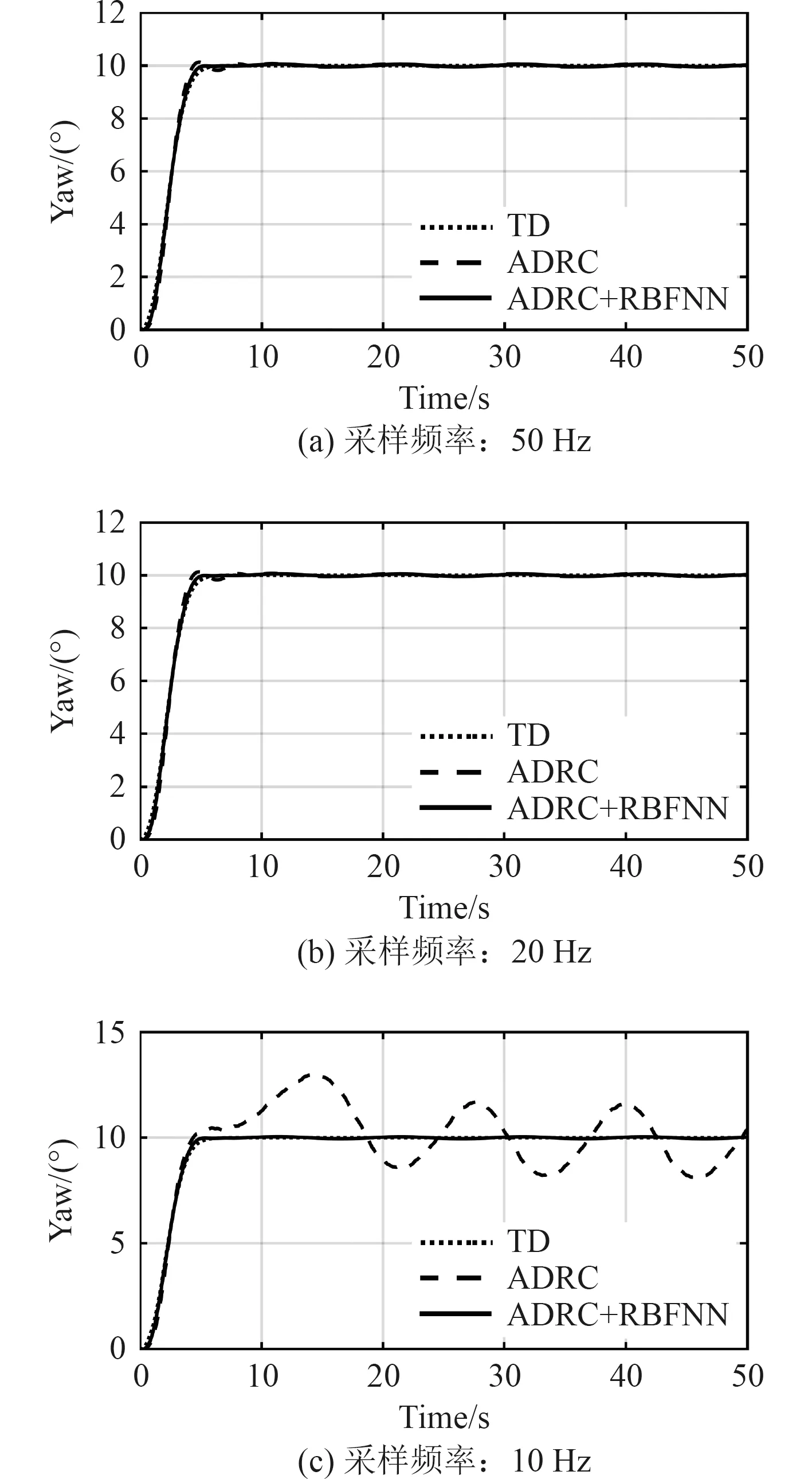
图12 不同采样频率航向角跟踪控制仿真结果Fig.12 Simulation results of yaw trajectory tracking control at different sampling frequencies

仿真结果说明改进后的ADRC+RBFNN 控制器在低采样频率下依然能够取得理想的控制效果，进而可以通过嵌入式系统硬件和工业软件组件的方式在实际AUV 平台中实现，具有很大的工程应用潜力。

4 结 语

针对AUV 作业过程中存在的环境干扰，为了提高在不同阶跃输入和采样频率下的扰动观测能力和抗干扰能力，本文提出一种基于RBF 神经网络补偿的新型自抗扰控制方法。在线性ADRC 控制的基础上，将自适应RBF 神经网络应用于改进扩张状态观测器，提升了扰动估计的快速性、准确性。仿真实验证明，改进后的ADRC 在不同阶跃输入下对扰动和系统状态的观测更加准确，控制器跟踪航向角能够更快达到稳定值，且适用于低采样频率。

后续工作将重点研究本文方法在AUV 平台中的应用问题，通过水池和开放水域实验验证本文提出方法的有效性。