矢量泵喷推进器尾流场特性及操纵性能研究
2023-11-24叶金铭邹笑宇郑子涵
叶金铭,邹笑宇,郑子涵,张 迪
(海军工程大学 舰船与海洋学院,湖北 武汉 430033)
0 引 言
潜艇作为国家战略性武器装备,低噪高效的推进性能、灵活机动的操纵性能是其战略意义的重要体现,改善潜艇推进性能、操纵性能和声隐身性能具有重大意义。目前各国已对潜艇推进器噪声进行了大量研究,发现推进器盘面处流场的均匀性与推进器噪声密切相关,而布置于潜艇推进器上游的尾舵会对桨盘面流场均匀性产生不利影响。矢量推进可通过在不同方向产生推力,使得推力矢量化[1]。从而替代尾舵的作用,很大程度上降低了潜艇推进器的噪声,因此矢量推进得到了越来越多的关注。
目前水下航行器实现矢量推进的方式主要分为螺旋桨式和喷水式。国内外学者对水下矢量推进器的研究主要集中在矢量推力对水下航行器操纵性能的影响及应用等方面[2]。国外使用螺旋桨式矢量推进器的水下航行器中具有代表性的是美国蓝鳍机器人公司生产的Bluefin-12,它是一种二自由度推进器,通过2 个电机带动推杆实现偏航和俯仰操纵[3–4,9]。潘存云等[5–7]分别基于球齿轮和锥齿轮设计出了2 款柔性推进机构,系统通过3 个运动传动链将动力传送到螺旋桨轴,可实现360°全方向偏转运动,优化了机构的运动特性。除了采用单一推进器的方式,还有在水下航行体不同位置不同方向布置多个推进器代替操舵实现矢量运动的方式。通过多个推进器协同工作,实现水下航行体的前进、倒车、悬停等动作。这种方式极大提高了水下航行体的操纵性。例如,英国BAE 公司在2009 年推出的“泰利斯曼”近海无人潜水器就使用的是多矢量推进器[8–9]。除了通过改变螺旋桨轴向位置实现矢量推进的螺旋桨式矢量推进器,还有通过改变出流方向实现矢量推进的喷水式矢量推进器。耿令波等[10]提出一种基于横向二次射流的水下推力矢量技术,以二次射流产生的横向速度影响主流方向发生偏转,通过数学模型证明了该矢量推进方式的可行性,并通过数值计算方法研究了射流参数对主流偏转角度的影响。
但目前所使用的矢量推进器无论是通过布置多个推进器还是基于附加机构的矢量推进器,都会增加推进器的结构体积,使得推进器的效率和噪声大幅度增加[11]。以往矢量推进器的研究忽略了布置于潜艇上的尾舵会对桨盘面流场均匀性产生不利影响,从而降低了潜艇的水动力性能和隐身性能。
为解决该问题,设计一种潜艇矢量泵喷推进器,以取消尾舵达到改善桨盘面流场的作用,进而降低泵喷推进器噪声。基于常规的矢量泵喷推进器计算方法对潜艇矢量泵喷推进器推进性能和操纵力特性进行研究,并将计算结果与常规的泵喷推进器对比,分析其水动力性能。
1 研究对象
以某潜艇为计算对象,包括艇体、指挥台围壳、围壳舵、尾舵、泵喷推进器,该潜艇艇长为7.76 m,航速为6 kn,排水量为3.787 t。潜艇尾舵为十字舵,分为稳定翼、方向舵、升降舵3 部分。泵喷推进器由导管、定子、转子组成,该泵喷推进器定子为13 叶,转子为7 叶,最大叶梢间隙为5 mm,最小叶梢间隙为3.5 mm。本文提出一种矢量泵喷推进器,取消了尾舵布置,在上述常规泵喷推进器基础上,在其导管尾部加装一个矢量喷管,轴向长度为导管长度LP的2/3。安装2 种泵喷推进器的潜艇模型对比如图1 所示。
2 数值计算方法
2.1 控制方程和湍流模型
在流体不可压缩的条件下,流场的连续方程和动量方程为:
式中:ui,uj分别为各速度分量的时间平均值(i=1, 2, 3,j=1, 2, 3) ;P为 压 力 的 时 间 平 均 值; ρ为 流 体 的 密度; µ为流体的动力粘性系数;gi为重力加速度分量;-ρu′iu′j为雷诺应力项。
本文研究的矢量泵喷推进器水动力性能计算和艇体绕流场计算问题适合使用复杂湍流的两方程雷诺应力模型,其主要有Standardk-ε湍流模型、Realizablek-ε 湍流模型以及SSTk-ω湍流模型。
其中SSTk-ω 湍流模型由于结合了k-ε 和k-ω的优势,适合于近壁面和远场的流体流动问题,其应用范围更广,计算精度更高。上述湍流模型推导过程与具体表达方程见参考文献[11]。
2.2 计算域和网格划分
对于泵喷推进器+潜艇模型的水动力计算问题,将计算域分为外域、导管内域、转子域3 部分,各部分通过交界面传递数据。其中,外域为静止域;外域形状选择圆柱体,进口边界条件为速度进口;到艇体前端距离为1L;出口边界条件为压力出口;距离艇体尾端为2L;侧面选择对称面;直径为2L。其中L为艇长,外域内边界为潜艇模型表面,采用无滑移壁面条件,如图2 所示。为减少交界面个数,将导管表面分为内外两部分,导管外壁划分到外域,作为外域内边界的一部分,导管内表面和导管进出口形成的类圆台区域作为导管内域的外边界,如图3 所示。

图2 外域设置Fig.2 Outer domain settings

图3 导管内域和转子域划分Fig.3 Division of inner domain and rotor domain
计算域采用结构网格和非结构网格相结合的方法进行划分。由于本文选择的潜艇模型外形复杂,尾十字舵稳定翼与转动舵之间间隙过小,使用结构网格进行划分难度较大,故外域使用STAR CCM+非结构网格生成器生成网格,艇体近壁面采用棱柱层网格模拟边界层流体流动。本文所用模型存在指挥台围壳、围壳舵及尾舵多个附体,对这些附体附近区域使用加密块进行加密,捕捉由附体引起的流场变化,进而使转子前流场符合实际情况,提高计算精度。导管内域和转子域流场变化复杂,精确预报泵喷推进器水动力性能对网格要求较高,故选择使用ICEM 网格划分软件生成与形状匹配度高的结构网格。导管内域和转子域都是回转体并且存在周向重复,可先对导管域和定子域进行分割,通过分块结构化网格划分方法建立单通道网格,再通过旋转得到全通道网格,节约了网格划分的时间。由于喷管结构简单,并且在后续计算中需改变喷管出口方向和几何形状,为便于操作节约时间,故将尾管划分到外域中,采用非结构网格模型快速生成外网格,导管内域及转子域各部分结构形状均未改变,故网格划分与常规泵喷推进器相同。具体网格划分如图4 所示。
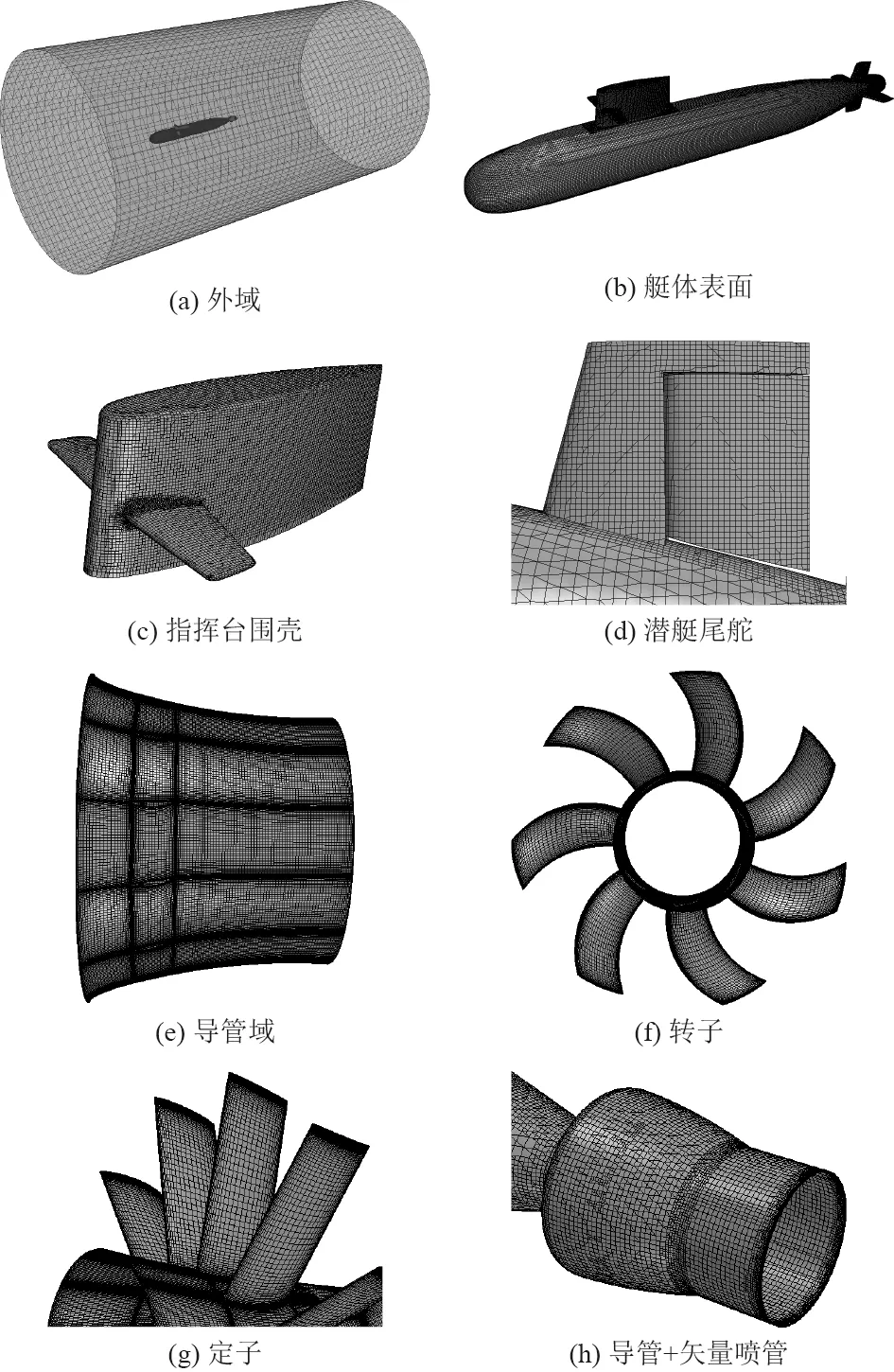
图4 网格划分Fig.4 Mesh division
2.3 网格无关性验证
网格疏密程度对于数值计算结果有一定影响,网格越密,计算结果越精确,但对计算机性能要求越高。因此需对计算所用网格进行无关性验证,在保证计算精度的情况下选择合适的网格密度进行计算。
通过改变基础尺寸和节点数量改变非结构和结构网格疏密程度,形成了3 套不同密度的网格,分别运用3 套网格计算常规泵喷推进器+潜艇模型水动力性能。网格数量及计算结果如表1 所示。
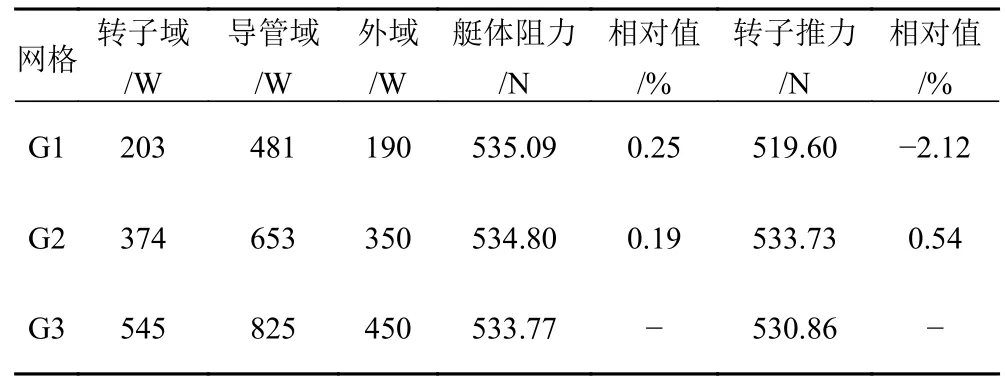
表1 不同网格密度计算结果对比Tab.1 Comparison of calculation results with different mesh densities
以最大网格数G3 为参照,比较不同网格密度下艇体阻力及转子推力的相对值,发现计算结果差别不大,艇体阻力相对值最大为0.25%,转子推力相对值最大为2.12%。考虑计算精度和计算时间,G2 网格已满足计算要求。
3 结果与分析
3.1 尾舵对转子盘面流场均匀性的影响
一般泵喷推进器处于尾舵后端,舵的存在会加剧转子盘面流场的紊乱程度。故需对泵喷推进器转子盘面流场均匀性进行研究,探究尾舵对流场均匀性的影响。针对无转子状态下有舵、无舵2 个模型进行计算,分别对应A 模型和B 模型。
坐标系采用笛卡尔坐标系,遵循右手定则,以潜艇首部顶点为坐标原点,x轴正方向指向潜艇前进方向,y轴正方向指向艇体左舷,z轴以垂直向上为正。
计算得到转子盘面轴向速度和周向速度分布,如图5 和图6 所示。对比图中不同模型轴向速度、周向速度分布,可看出无舵情况下转子盘面流场更均匀,这证明了尾舵对泵喷推进器转子盘面流场有不利影响。对于无舵模型转子盘面轴向速度和周向速度都存在一定的周期性,是由于流体流过定子时流体黏性影响使定子近壁面速度降低导致速度周期性变化;在转子盘面上半部分速度分布相对下半部分更加不均匀,这主要是指挥台围壳尾流向下游流动对转子盘面流场均匀性的影响。
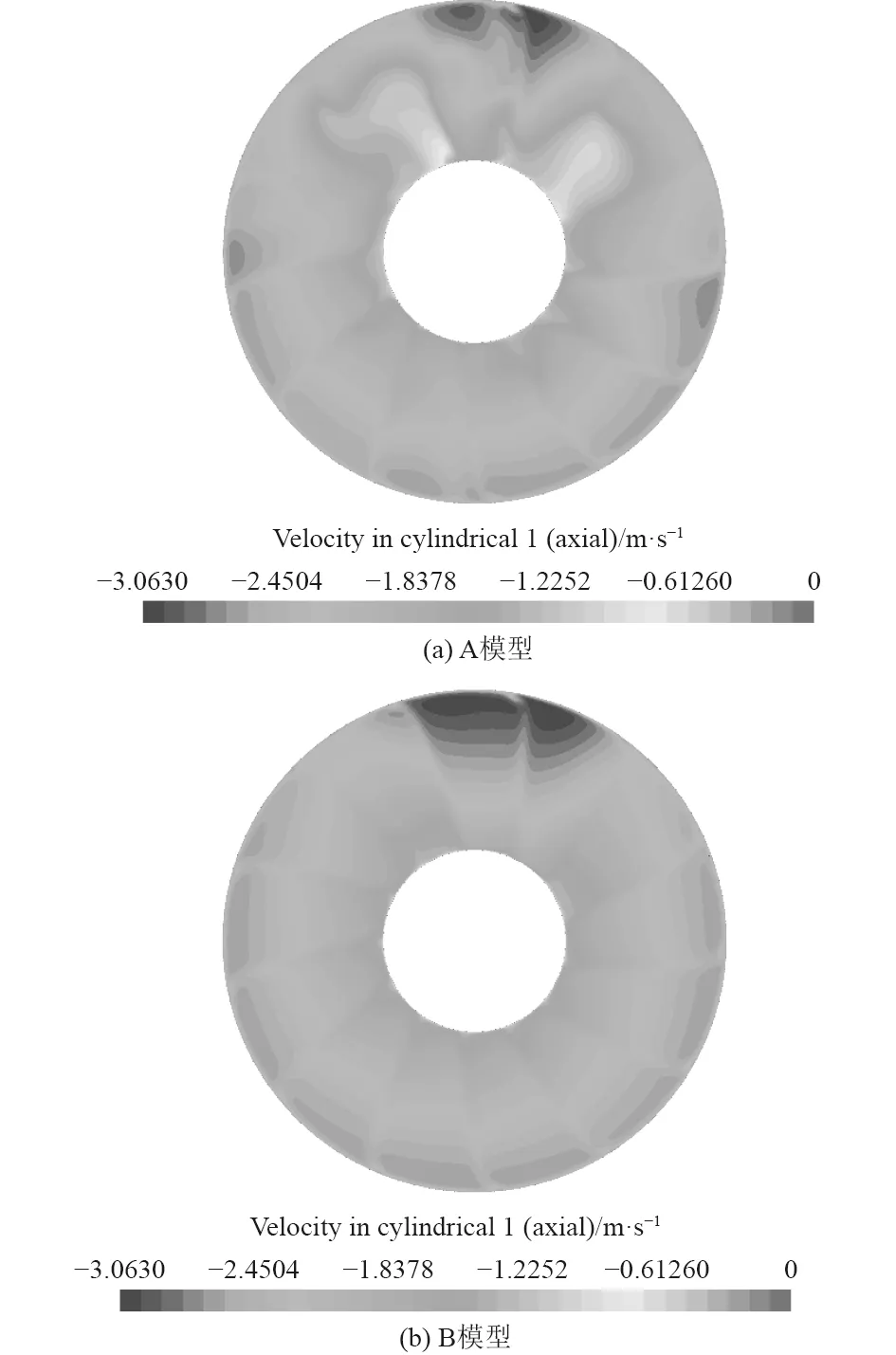
图5 不同模型转子盘面流场轴向速度分布云图Fig.5 Axial velocity distribution cloud charts of rotor disk flow field in different models

图6 不同模型转子盘面流场周向速度分布云图Fig.6 Circumferential velocity distribution cloud charts of rotor disk flow field in different models
为定量分析不同模型转子盘面处流场分布情况,对0.4R、0.6R、0.8R处速度分布情况进行研究,其中R为螺旋桨半径,对速度进行无因次化Va/U0、Vt/U0,Va为 轴向速度,Vt为周向速度,U0为进口速度,如图7和图8 所示。图中角度以潜艇左舷为0°,从艇尾向艇首看顺时针旋转360°。可以看出无论是轴向速度还是周向速度无舵模型的速度分布曲线都较有舵模型波动程度低,说明了尾舵的存在加剧了转子盘面流场的不均匀性。
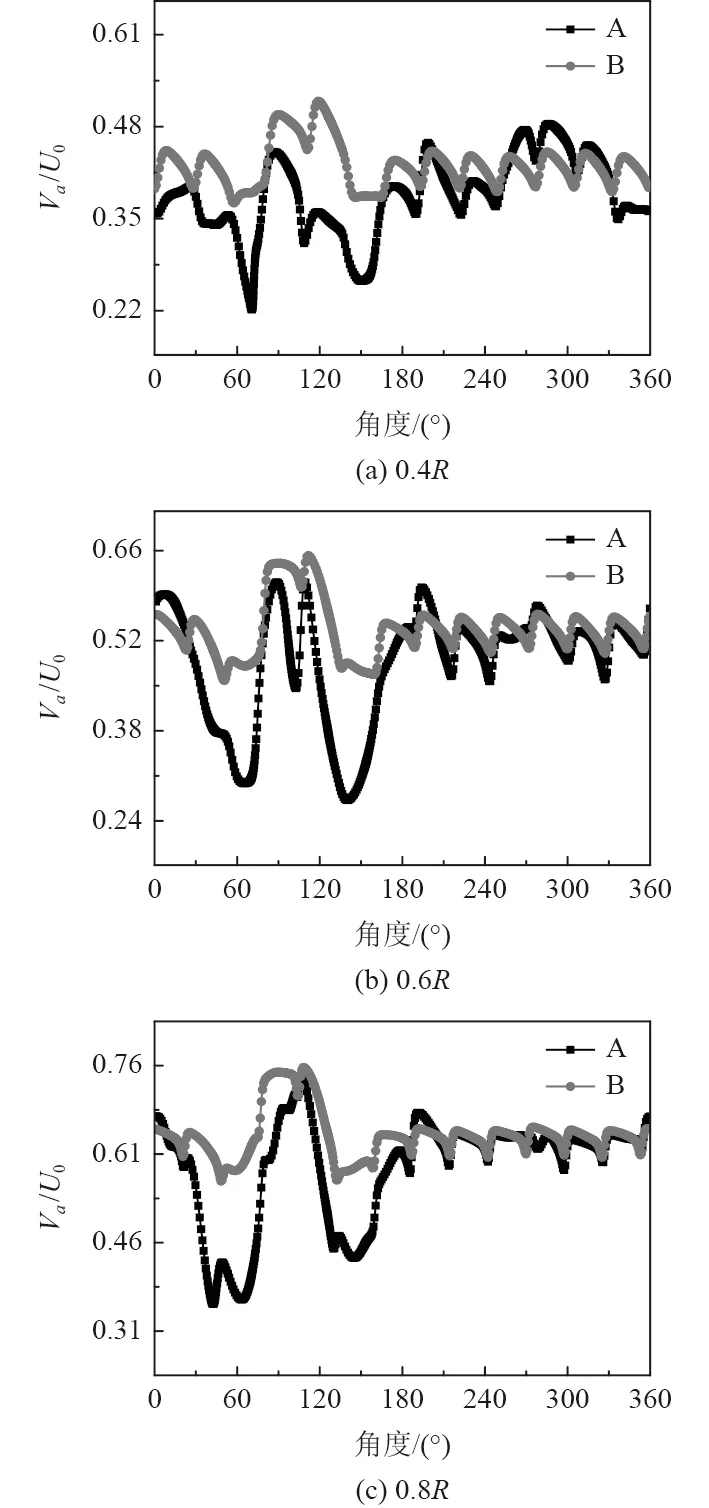
图7 不同模型转子盘面流场轴向速度分布Fig.7 Axial velocity distribution of rotor disk flow field in different models

图8 不同模型转子盘面流场周向速度分布Fig.8 Circumferential velocity distribution of rotor disk flow field in different models
3.2 矢量泵喷推进器对潜艇推进效率的影响
首先对无推进器潜艇模型水动力进行计算,得到艇体阻力RS= 448.47 N,RS由裸艇体、指挥台围壳和围壳舵3 部分组成,不包括尾舵的阻力。
对潜艇分别安装常规泵喷推进器和矢量泵喷推进器的水动力性能进行计算,先对模型进行定常计算,然后在定常计算结果基础上更换非定常计算模型进行计算,采用此方法的优点在于定常计算稳定结果作为非定常计算初始状态可加快计算收敛速度,节约计算时间和计算成本。在非定常计算阶段对转子域采用滑移网格模拟转子绕轴旋转,为保证计算精度,计算时间步长设置为每个时间步内转子旋转2°。
通过改变转子转速使潜艇+泵喷推进器整体合力为0,得到常规泵喷推进器转速为720 r/min,矢量泵喷推进器转速为712.56 r/min。矢量泵喷推进器+潜艇模型相对常规泵喷推进器+潜艇模型来说,在泵喷推进器上游不再布置尾舵,故整个系统阻力减小,转子需提供的推力也相应减小,转速相对降低就可保证合力为0。
通过数值计算得到2 种泵喷推进器+潜艇模型各部分沿x轴方向力的大小,结果如表2 所示。可以看出2 种泵喷推进器+潜艇模型在相应转速下合力基本为0,可认为2 种模型基本达到平衡状态。通过对比2 种泵喷推进器+潜艇模型各部分产生轴向力大小,发现尾舵或者尾管均产生阻力,但尾舵阻力明显高于尾管。

表2 两种泵喷推进器+潜艇模型水动力数据对比Tab.2 Comparison of hydrodynamic data of two pump-jet propulsion + submarine models
推进效率作为衡量泵喷推进器推进性能的重要指标,对比了2 种泵喷推进器的水动力参数,如表3 所示,计算公式为:

表3 2 种泵喷推进器水动力参数Tab.3 Hydrodynamic parameters of two kinds of pump-jet propulsion
式中:RS为无推进器潜艇模型艇体阻力,由于矢量泵喷推进器系统中矢量喷管为推进器的一部分,而常规泵喷推进器+潜艇模型中尾舵与矢量喷管作用相同,为保持一致,在计算艇体阻力时并不包括尾舵阻力,而将尾舵看作推进器的一部分。VS为 潜艇航速;n为转子转速;QR为 转子扭矩;PE为有效功率;PD为收到功率; ηD为推进效率。
从表3 可看出,常规泵喷推进器收到功率为2.748 kW,矢量泵喷推进器收到功率为2.292 kW,比常规泵喷推进器降低了16.6%,可认为推进效率提高了19.9%。通过对2 种泵喷推进器推进效率的比较,充分说明了在相同航速下,潜艇采用矢量泵喷推进器可以提高推进效率。这主要是因为矢量泵喷推进器+潜艇模型相对常规泵喷推进器+潜艇模型取消了尾舵的布置,整个系统阻力减小,泵喷推进器收到功率降低,推进效率提高。
3.3 矢量泵喷推进器的操纵性能
由于矢量泵喷推进器通过矢量喷管的偏转实现了推力的矢量化,可提供潜艇改变航向所需的横向力及力矩,从而取代了常规泵喷推进器+潜艇整体模型中的尾舵,故需对矢量泵喷推进器的操纵力特性进行研究,并与尾舵进行对比,衡量潜艇使用矢量泵喷推进器代替尾舵对航行机动性的影响。
对不同矢量喷管偏转角度的矢量泵喷推进器水动力性能进行数值计算,得到不同偏转角度与矢量喷管+导管产生横向力之间的关系,并与尾舵产生横向力进行比较,得到了两者之间的对应关系。
3.3.1 计算模型
矢量泵喷推进器是以常规泵喷推进器为基础在其尾部加装一个矢量喷管,矢量喷管轴向长度初步选择为导管长度的2/3,以导管尾端面为基础平面,以中轴线为母线拉伸,得到矢量喷管几何模型。通过改变矢量喷管母线偏转角度控制矢量喷管的偏转角度,如图9 所示, θ为偏转角。由于矢量喷管向左舷或者右舷偏转相同角度产生横向力相同,故只需计算偏转一个方向即可,本文选择向潜艇左舷偏转进行研究。由于潜艇一般操舵角度为 ±30◦,所以选择在0°~ 30°范围内每隔5°取一个偏转角建模,形成了0°、5°、10°、15°、20°、25°、30°七个导管+矢量喷管模型。
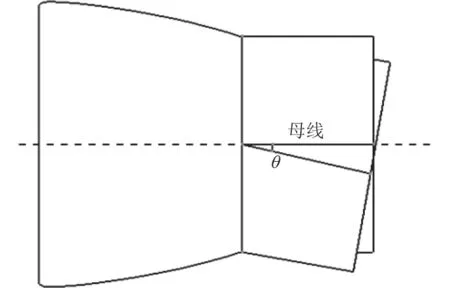
图9 矢量喷管偏转示意图Fig.9 Deflection diagram of vector pump-jet propulsion
3.3.2 2 种泵喷推进器横向力及偏转力矩对比
为比较潜艇采用不同泵喷推进器对潜艇航行机动性的影响,对尾舵和矢量喷管操纵力进行比较。由于矢量泵喷推进器中导管和矢量喷管为整体模型,计算横向力时为两部分合力,为控制变量。在计算尾舵横向力时需考虑常规泵喷推进器导管产生的横向力。
图10 和图11 分别为尾舵+导管横向力及偏转力矩和矢量喷管+导管横向力及偏转力矩随偏转角度的变化曲线。可看出,在0°~30°操舵舵角范围内,常规泵喷推进器+尾舵产生的横向力和偏转力矩随着尾舵偏转角度的增加先增大后减小。在偏转角度为25°时达到最大值,偏转角度继续增大后横向力和偏转力矩急剧降低,出现失速现象。而矢量泵喷推进器产生的横向力和偏转力矩随着偏转角度的增加而增大,没有出现失速现象。

图10 不同泵喷推进器横向力曲线Fig.10 Transverse force curves of different pump-jet thrusters

图11 不同泵喷推进器偏转力矩曲线Fig.11 Deflection moment curves of different pump-jet thrusters
在0°~30°操舵舵角范围内,矢量推进器的最大横向力与尾舵+导管相当,但最大偏转力矩大于常规泵喷推进器+尾舵的偏转力矩;在相同的操舵角度下,矢量泵喷推进器偏转力矩均大于常规泵喷推进器,说明矢量泵喷推进器具有良好的航行机动性;在偏转力矩相同情况下,矢量泵喷推进器矢量喷管偏转小于常规泵喷推进器尾舵舵角。
通过图11 可大致推算出,产生相同的横向力时,常规泵喷推进器尾舵偏转5°、10°分别对应矢量泵喷推进器矢量喷管偏转2.8°、7.16°,为比较推进器产生等大横向力时的偏转力矩,对偏转角度2.8°、7.16°的矢量泵喷推进器水动力进行计算,并与常规泵喷推进器尾舵+导管产生横向力比较,计算结果如表4所示。可知,在2 种泵喷推进器横向力基本相同时,矢量泵喷推进器偏转力矩大于常规泵喷推进器,矢量喷管偏转角度比尾舵小,有利于降低泵喷推进器在操舵工况下转子盘面流场不均匀性。
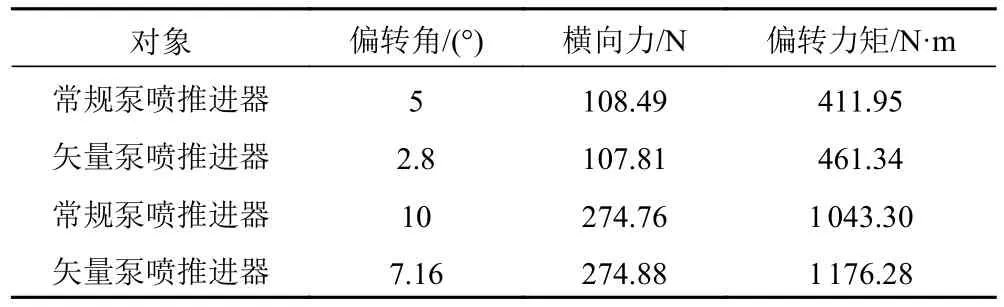
表4 不同泵喷推进器不同偏转角度横向力及偏转力矩Tab.4 Lateral force and deflection moment of different pump-jet thrusters at different deflection angles
4 结 语
本文对比分析带尾舵+泵喷推进器潜艇模型与无尾舵+矢量泵喷推进器潜艇模型的水动力性能,得到了以下结论:
1)通过比较转子盘面处轴向速度和周向速度分布,说明了尾舵的存在对转子盘面处流场均匀性不利。
2)由于矢量泵喷推进器+潜艇模型取消了尾舵的布置,整体模型总阻力减小,矢量泵喷推进器收到功率降低,推进效率提高,说明矢量泵喷推进器推进性能比常规泵喷推进器好。
3)在0°~30°操舵舵角范围内,矢量推进器最大偏转力矩大于常规泵喷推进器+尾舵的偏转力矩。在相同的操舵角度下,矢量泵喷推进器偏转力矩均大于常规泵喷推进器,说明矢量泵喷推进器具有良好的航行机动性。
4)在偏转力矩相同情况下,矢量泵喷推进器矢量喷管偏转小于常规泵喷推进器尾舵舵角,有利于降低泵喷推进器在操舵工况下转子盘面流场不均匀性。
