柔直换流器单滑模观测器电网电压观测方法

郝良收，夏克鹏，陈小平，江海，朱启，王迪

（1.中国南方电网超高压输电公司天生桥局，贵州 兴义 562400；2.许继集团有限公司，河南 许昌 461000；3.许继电气股份有限公司，河南 许昌 461000）

随着可再生能源并网发电技术的飞速发展，如何避免弃风、弃光，提高可再生能源的消纳能力，已成为学界和业界广泛关注的焦点[1-2]。

受我国国情的限制，光伏、风电等可再生能源资源大都分布于西北地区，而经济发达地区则主要位于东南沿海一带。如何实现可再生能源西电东送，增强可再生能源的消纳能力，缓解能源危机和缓解污染等问题，已成为亟待解决的关键问题。在此背景下，柔性直流输电技术应运而生，并在近年来得到蓬勃发展[3-4]。

柔直换流器是柔性直流输电系统中的关键核心装备，主要用于实现高压大功率电能变换与控制。因此，研究提高柔直换流器的运行稳定性和可靠性的控制方法，对提高柔性直流输电系统的运行稳定性、增强可再生能源的消纳能力具有重要意义和价值[5-8]。

通常情况下，为了实现柔直换流器的控制，往往需要同时采样电网电压、电流等信息。然而，一旦电压或电流传感器出现故障，势必将降低柔直换流器的运行可靠性，进而降低柔性直流输电系统的运行可靠性[9-10]。

为了解决柔直换流器电网电压传感器故障容错控制问题，文献[11-14]研究了柔直换流器的无电网电压传感器控制方法。其中，文献[11]研究了基于虚拟磁链的无电网电压传感器控制方法。然而，常规虚拟磁链估计方法需要使用纯积分运算，而纯积分运算受采样直流偏置和积分初始值的影响较大。文献[12]在时域内研究了改进的柔直换流器虚拟磁链估计方法，消除了直流偏置的影响。文献[13]研究了一种改进的虚拟磁链观测方法，采用低通滤波器代替纯积分运算。然而，该方法需要对虚拟磁链进行相位幅值补偿。为了解决该问题，文献[14]提出了一种基于二阶低通滤波器的虚拟磁链观测方法。通过设计二阶低通滤波器，既可以克服纯积分运算的缺点，也避免了进行相位幅值补偿。

另一方面，文献[15-19]研究了基于电网电压观测的无电压传感器控制方法。其中，文献[15-16]提出了基于二阶广义积分器的电网电压开环观测方法。然而，该方法需要同时使用4 个二阶广义积分器，增加了算法计算量。为此，文献[17]提出了一种基于二阶低通滤波器的电网电压开环观测方法。所提方法仅需要使用2个二阶低通滤波器，从而减小了计算复杂度。文献[15-17]所提方法均为开环估计方法，其动态特性较慢。为此，文献[18]提出了一种基于闭环滑模观测器的电网电压观测方法。然而，该方法还需要增加低通滤波器和补偿算法。为了避免使用低通滤波器，文献[19]提出了一种基于改进型二阶滑模观测器的电网电压观测方法。所提方法通过设计非线性滑模面，消除了滑模抖振，避免了使用低通滤波器和补偿算法。然而，该方法仍然需要同时设计2 个滑模观测器，以实现电网电压在静止α-β坐标系上两个分量的观测。此外，文献[15-19]所提电网电压观测方法还受直流偏置的影响，一旦采样的信号中含有直流偏置，将会显著降低电网电压观测精度。

为了简化电网电压观测算法，并克服直流偏置的影响，本文提出了一种基于单滑模观测器和单三阶广义积分器的柔直换流器电网电压观测方法。所提方法仅需要设计1 个滑模观测器、采用1 个三阶广义积分器即可实现α轴和β轴电网电压的观测，并克服直流偏置的影响。与文献[15-19]所提常规方法相比，所提方法既可以降低计算复杂度，又可以实现直流偏置抑制。理论分析、对比仿真和实验研究验证了所提方法的有效性。

1 柔直换流器的并网数学模型

图1给出了典型的基于模块化多电平变换器的柔直换流器拓扑。其中，Lg1～Lg6为6个桥臂电感。

图1 柔直换流器拓扑Fig.1 Topology of flexible DC power converter

根据基尔霍夫电压定律和图1，可得柔直换流器输出电压与电网电压之间的关系为

式中：Lf为滤波电感；R为滤波电阻；uga，ugb，ugc分别为柔直换流器输出的三相电压；iga，igb，igc分别为三相并网电流；ega，egb，egc分别为三相电网电压。

将式（1）变换到两相静止α-β坐标系上可得：

式中：下标α，β表示电压、电流在两相静止α-β坐标系中对应的变量。

文献[15-17]根据式（2）设计了基于二阶广义积分器和二阶低通滤波器的电网电压观测方法。文献[18-19]则根据式（2）设计了基于滑模观测器的电网电压观测方法。为了简化电网电压观测方法，并克服直流偏置的影响，本文根据式（2）提出了一种基于单滑模观测器和单三阶广义积分器的电网电压观测方法。

2 基于滑模观测器的电网电压观测方法设计

2.1 滑模观测器设计方法

由文献[18]可知，根据式（2）可设计二阶滑模观测器以观测电网电压。二阶滑模观测器如下式所示：

由式（2）和式（3）可知，电流误差状态方程满足下式：

其中

为了保证滑模观测器收敛，需满足：

考虑到igα和igβ的对称性，以下以igα为例进行分析。

由式（4）和式（5）可得：

当Δigα＞0时，由式（6）可得：

当Δigα＜0时，由式（6）可得：

由式（7）和式（8），并结合igα和igβ的对称性可知，为保证滑模观测器收敛，m需满足：

当滑模观测器收敛时，电流误差及其微分收敛到零，此时可得电网电压egα和egβ满足：

然而，由于当电流收敛时，电流误差将在零附近波动，因此式（10）中的符号函数将会产生大量高频滑模噪声，这导致无法使用式（10）直接观测电网电压。为解决该问题，文献[18]提出了采用低通滤波器滤除高频滑模噪声的方法，但这会影响电网电压基波的观测。

为了滤除高频滑模噪声，并避免影响基波电网电压，本文提出了采用二阶广义积分器代替低通滤波器的电网电压观测方法。

2.2 基于二阶广义积分器的电网电压观测方法

根据文献[15-16]，二阶广义积分器的控制框图如图2所示，其传递函数为

图2 二阶广义积分器框图Fig.2 Block diagram of the second-order generalized integrator

由式（11）可得：

这表明二阶广义积分器对频率为ωg的信号不产生任何相位偏移和幅值衰减。同时，二阶广义积分器还可以抑制其他频率的信号，如图3所示。因此，可以利用二阶广义积分器代替低通滤波器观测频率为ωg的电网电压信号，并滤除高频滑模噪声的影响。

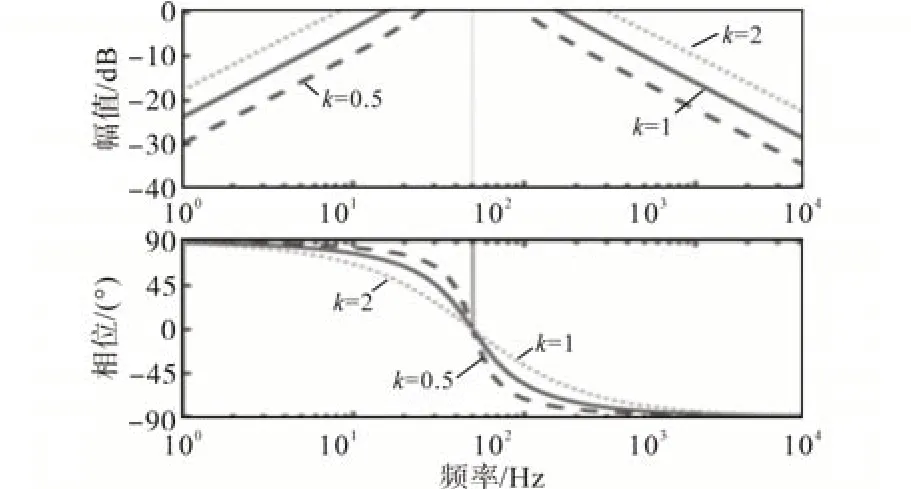
图3 二阶广义积分器波特图Fig.3 Bode diagram of the second-order generalized integrator

基于滑模观测器和二阶广义积分器的电网电压观测方法控制框图如图4所示。

图4 基于滑模观测器和二阶广义积分器的电网电压观测方法控制框图Fig.4 Control diagram of the grid voltage observation method based on sliding mode observer and second-order generalized integrator

由上述分析可知，与文献[18]相比，本文所提基于滑模观测器和二阶广义积分器的电网电压观测方法虽然不需要再进行相位幅值补偿，但仍需要设计2 个滑模观测器和2 个二阶广义积分器以分别观测egα和egβ，如图4所示，这会增加算法的计算复杂度。

3 基于单滑模观测器的电网电压观测方法设计

为降低电网电压观测算法的计算复杂度，本文进一步提出了一种改进的基于单滑模观测器的电网电压观测方法。

3.1 基于单滑模观测器和单二阶广义积分器的电网电压观测方法

第2.2 节提出了一种基于滑模观测器和二阶广义积分器的电网电压观测方法，但该方法未充分利用二阶广义积分器的特点。如文献[15-16]所述，二阶广义积分器还可以输出一个正交信号。因此，还可以结合二阶广义积分器这一特点对第2 节所设计的电网电压观测方法进行改进。

由图2可知uout2与uin的传递函数为

由式（13）可知：

这表明二阶广义积分器的输出信号uout2为输入信号uin的正交信号，两者频率和幅值相等，但uout2滞后uin90°。又考虑到uin和uout1相同，因此可知uout2滞后uout190°。

根据该分析可知，若根据图4所示二阶广义积分器模块观测出了电网电压êgα，则二阶广义积分器的另一输出信号就是êgβ。因此，当使用滑模观测器和二阶广义积分器观测电网电压时，可充分利用二阶广义积分器的特点，仅使用1 个滑模观测器和1个二阶广义积分器即可同时实现电网电压êgα和êgβ的观测。这显著降低了电网电压观测算法的计算复杂度。该方法的原理见图4上半部分所示。

然而，当仅使用一个二阶广义积分器时，其输出信号uout2受直流偏置影响较大，这是因为G2（s=0）=k。因此，若采样的电压和电流中含有直流偏置，则观测的电网电压êgβ将受直流偏置的影响。为了消除直流偏置的影响，本文进一步设计了一种改进的基于单滑模观测器和单三阶广义积分器的电网电压观测方法。

3.2 基于单滑模观测器和单三阶广义积分器的电网电压观测方法

三阶广义积分器的控制框图如图5所示[20]。与图2所示二阶广义积分器相比，三阶广义积分器是在二阶广义积分器的基础上增加了一条支路，用于实现直流偏置抑制。

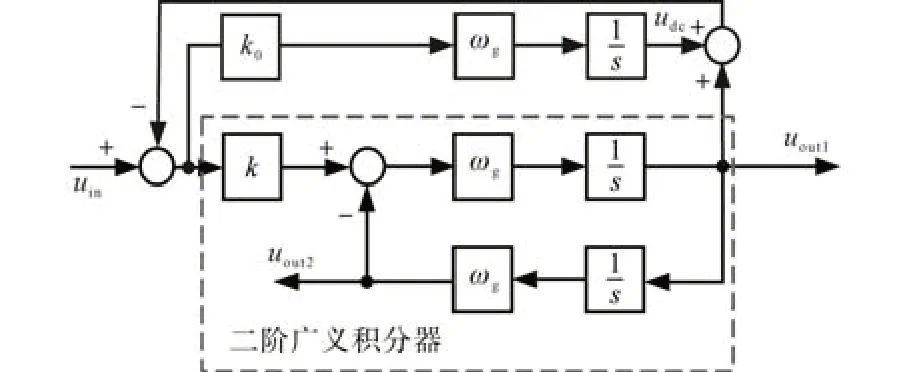
图5 三阶广义积分器框图Fig.5 Block diagram of the third-order generalized integrator

由图5可知，三阶广义积分器的传递函数满足：

由式（15）可得：

由式（17）可知，三阶广义积分器的输出uout1和uin相同，且可以实现直流偏置抑制。这与常规二阶广义积分器输出一样。

由式（16）可得：

由式（18）可知，三阶广义积分器的输出uout2和uin正交，这与常规二阶广义积分器输出一样。然而，与常规二阶广义积分器不同的是，三阶广义积分器的输出uout2可以消除直流偏置的影响。因此，当采用三阶广义积分器代替二阶广义积分器时，可以实现直流偏置抑制。

综合上述分析，当采用三阶广义积分器代替二阶广义积分器时，可构建基于单滑模观测器和单三阶广义积分器的电网电压观测方法，如图6所示。

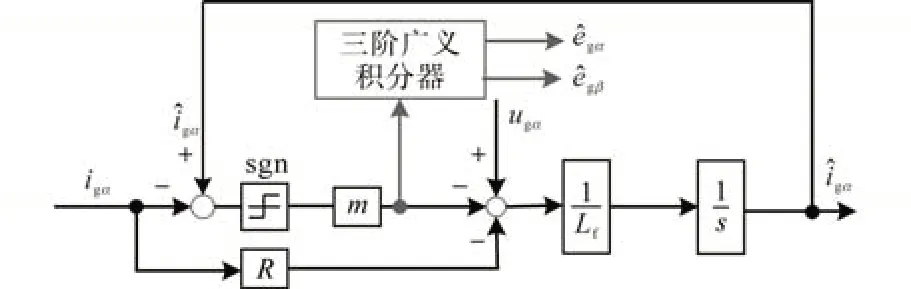
图6 基于单滑模观测器和单三阶广义积分器的电网电压观测方法控制框图Fig.6 Control diagram of the grid voltage observation method based on single sliding mode observer and single third-order generalized integrator

为了突出本文所提方法的优点，表1 对比了本文所提方法与文献[15-19]所提方法的各自优缺点。由表1 可见，本文所提方法不仅需要较少的滤波器数量和观测器数量，而且具有直流偏置抑制能力，体现了所提方法的优点。

表1 不同方法的对比Tab.1 Comparison of different methods

3.3 三阶广义积分器参数设计

式（10）给出了电流收敛后真实电网电压与滑模函数的关系。为了消除滑模抖振，本文采用三阶广义积分器求取观测的电网电压êgα和êgβ。因此，由式（10）、式（15）、式（16）和图6可知，观测的电网电压和实际电网电压之间的关系为

由此可知，传递函数G3（s）和G4（s）中的两个系数k和k0决定着电网电压观测的动稳态特性。为此，图7 给出了k和k0变化时传递函数G3（s）和G4（s）的波特图。

图7 传递函数G3（s）和G4（s）的波特图Fig.7 Bode diagram of the transfer function G3（s）and G4（s）

由图7a 和图7b 可见，当k0不变时，增大k有助于提高传递函数G3（s）的带宽，从而提高电网电压egα观测的动态特性，但k增大时，滑模噪声会被放大。因此，k需要折中选择。此外，对比图7a和图7b可见，k0对G3（s）波特图的影响较小。

由图7c 和图7d 可见，当k不变时，k0变化对传递函数G4（s）的高频特性几乎没有影响，但k0增大时，G4（s）的低频增益有所减小，表明其直流偏置信号的衰减能力增强。然而，k0过大时，G4（s）抑制直流偏置的动态特性会有所减慢。因此，k0也需要折中选择。综合上述分析，本文选择k=1，k0=0.25。

4 仿真和实验验证

4.1 仿真验证

图6给出了本文所提基于单滑模观测器和单三阶广义积分器的电网电压观测方法的控制框图。该方法不仅可以降低计算复杂度，而且可以实现直流偏置抑制。

为了验证该方法的有效性，本节建立了仿真模型，并进行了对比仿真研究。仿真时，滤波电感为10 mH，滤波电阻为1 Ω，电网相电压峰值为90 V，电网频率为50 Hz。首先，为了验证参数k和k0对电网电压观测的影响，进行了对比仿真研究。仿真结果如图8、图9所示。

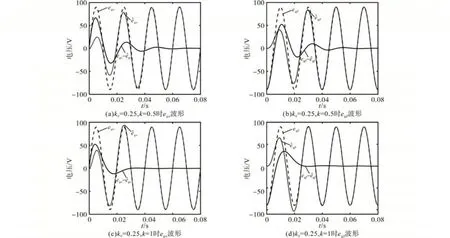
图8 k和k0变化时电网电压动态收敛波形Fig.8 Dynamic convergence waveforms of grid voltage when k and k0 change

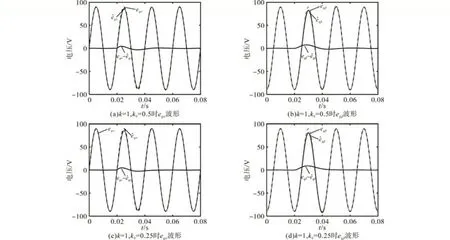
图9 突加直流偏置且k和k0变化时电网电压动态收敛波形Fig.9 Dynamic convergence waveforms of grid voltage when DC-offset is added with varied k and k0

图8a 和图8b 给出了k0=0.25，k=0.5 时本文所提方法的电网电压动态收敛波形。图8c 和图8d则给出了k0=0.25，k=1 时本文所提方法电网电压动态收敛波形。对比图8a和图8c可见，当k由0.5增大到1 时，电网电压动态收敛速度加快。由图8b 和图8d 也可以得到相同的结论。这与理论分析一致。然而，如果k过大，滑模噪声会被放大，这会增大电网电压的谐波，并降低系统的稳定性。

图9 测试了在0.02 s 突加直流偏置时k0和k变化对电网电压观测的影响。仿真时，在0.02 s时突然给ugα加上-10 V 的直流偏置。图9a 和图9b 给出了k=1，k0=0.5 时本文所提方法电网电压动态收敛波形。图9c 和图9d 则给出了k=1，k0=0.25时本文所提方法电网电压动态收敛波形。

由图9可见，当突加直流偏置时，电网电压观测误差经过一个暂态后趋近于零。这表明本文所提方法几乎可以完全消除直流偏置对电网电压观测的影响，验证了本文所提基于单滑模观测器和单三阶广义积分器的电网电压观测方法的可行性。此外，对比图9a 和图9c 可见，当k0减小时，本文所提方法在突加直流偏置时的电网电压动态收敛速度有所加快，这也与理论分析一致。

图10进一步给出了本文第3.1节所提基于单滑模观测器和单二阶广义积分器的电网电压观测方法在突加直流偏置时的电网电压收敛波形。仿真时，取k=1。为了方便起见，这里称该方法为常规方法。

图10 突加直流偏置时常规方法的电网电压动态收敛波形Fig.10 Grid voltage dynamic convergence waveforms of conventional method when DC-offset is added suddenly

由图10a 可见，常规电网电压观测方法得到的电网电压egα不受直流偏置的影响。这是因为图2所示二阶广义积分器的输出uout1不受直流偏置的影响。然而，由理论分析可知，图2所示二阶广义积分器的输出uout2受直流偏置的影响。因此当使用单个二阶广义积分器观测电网电压egβ时，egβ会受直流偏置的影响。由图10b 可见，当在0.02 s 突加直流偏置时，观测的电网电压egβ出现了一个明显的偏置误差，这验证了理论分析的正确性。正是为了解决该问题，本文提出了采用三阶广义积分器代替二阶广义积分器的电网电压观测方法，从而克服了直流偏置的影响，如图9所示。

4.2 实验验证

为了进一步验证本文所提基于单滑模观测器和单三阶广义积分器的电网电压观测方法的有效性，本节进行了实验研究。实验所用参数与仿真一致。

图11给出了常规方法和本文所提方法的电网电压动态收敛过程波形。对比图11可见，本文所提方法虽然将广义积分器的阶次由二阶提高到三阶，但其动态收敛速度和常规方法基本相同，这表明本文所提电网电压观测方法具有较好的动态收敛特性。

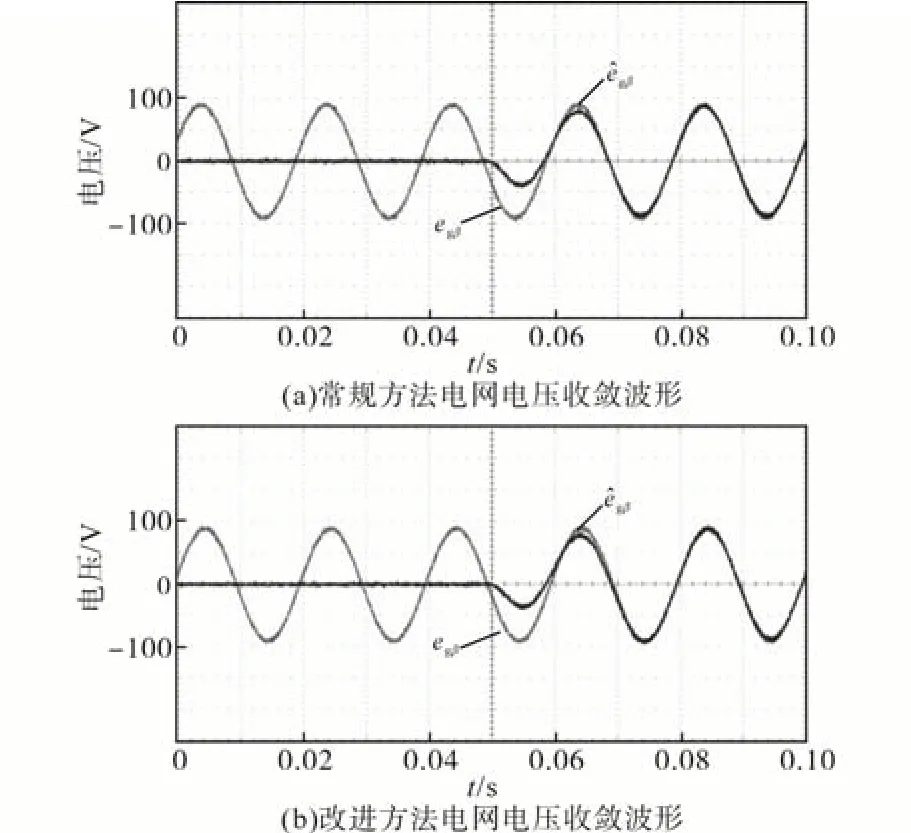
图11 电网电压动态收敛实验波形Fig.11 Dynamic convergence experimental waveforms of the grid voltage

此外，由于本文所提方法采用三阶广义积分器代替常规的二阶广义积分器，其对直流偏置的抑制能力也显著增强。为了验证所提方法对直流偏置的抑制能力，图12 和图13 分别对比了在ugα上突然减去10 V 和-10 V 直流偏置uαdc时常规方法和本文所提方法的电网电压观测波形。

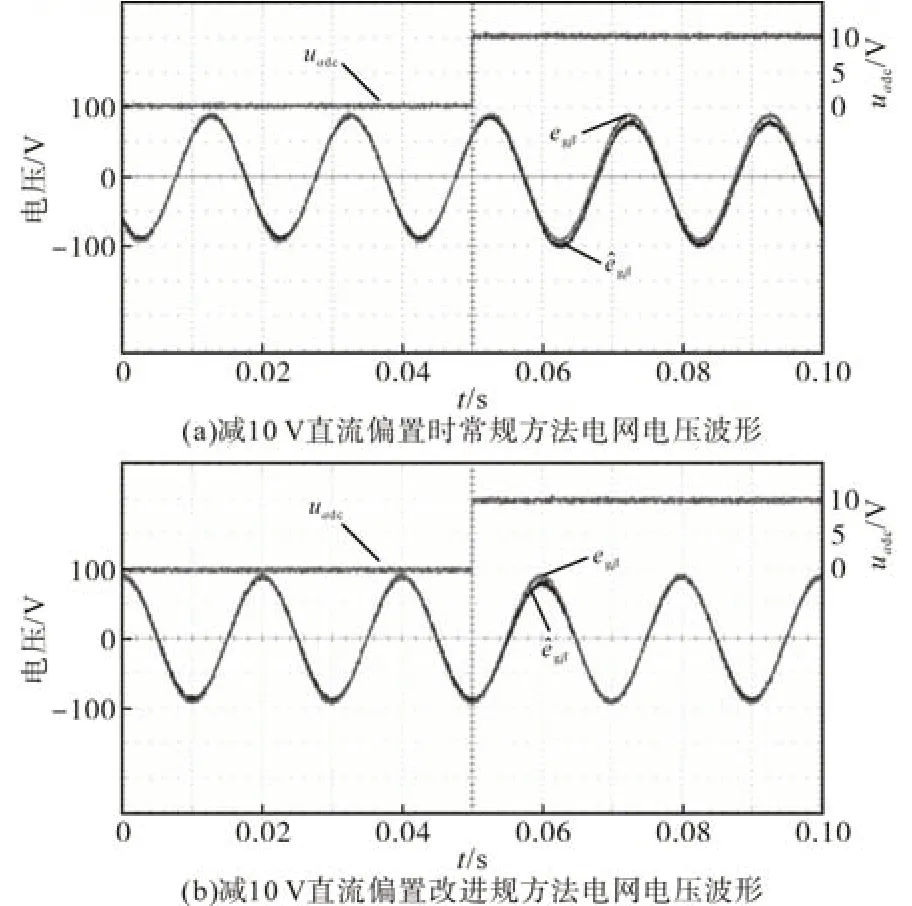
图12 减10 V直流偏置时电网电压实验波形Fig.12 Experimental waveforms of the grid voltage when 10 V DC-offset is subtracted

图13 减-10 V直流偏置时电网电压实验波形Fig.13 Experimental waveforms of the grid voltage when-10 V DC-offset is subtracted

对比图12a 和图12b 可见，当在0.05 s 突减10 V 直流偏置时，常规电网电压观测方法得到的电网电压明显出现了直流偏置，而本文所提基于单滑模观测器和单三阶广义积分器的电网电压观测方法经过一个暂态后，电网电压观测误差几乎为零。这表明了本文所提方法可以实现直流偏置抑制，与理论分析和仿真结果一致。

进一步由图13可见，当突减-10 V直流偏置时，与常规方法相比，本文所提方法仍然可以实现直流偏置抑制，再次验证了本文所提方法的有效性。

5 结论

本文提出了一种基于单滑模观测器和单三阶广义积分器的柔直换流器电网电压观测方法，以简化算法，并克服直流偏置的影响。本文首先分析了二阶广义积分器的输入输出特性，并充分结合二阶广义积分器的优势，设计了一种基于单滑模观测器和单二阶广义积分器的电网电压观测方法。针对二阶广义积分器不能抑制直流偏置的问题，本文又分析了三阶广义积分器的输入输出特性，并进一步提出了一种基于单滑模观测器和单三阶广义积分器的电网电压观测方法，以消除直流偏置的影响。理论分析、对比仿真和实验结果表明，本文所提方法具有如下突出优势：

1）与常规电网电压观测方法相比[15-19]，本文所提方法减少了观测器和滤波器的数量，从而显著简化了算法的设计和实现复杂度。

2）对比实验结果表明，本文所提方法与常规基于二阶广义积分器的方法具有类似的电网电压动态收敛过程。

3）对比仿真和实验结果表明，与常规方法相比，本文所提方法采用三阶广义积分器代替二阶广义积分器进行电网电压观测，从而克服了直流偏置的影响，提高了电网电压观测精度。

理论分析、仿真结果和对比实验结果验证了所提方法的有效性。