基于ACNS-MADS 的上下料口布局与配置联合优化
2023-11-22谢洁明陈庆新张惠煜
谢洁明,陈庆新,毛 宁,张惠煜
(广东工业大学 广东省计算机集成制造系统重点实验室,广东 广州 510006)
在产品高度个性化定制的市场需求下,考虑有限能力的物料储运系统 (finite capacity material handling system, FCMHS) 的单元流水式车间受到越来越多的关注[1-3]。设施布局与资源配置问题是离散制造系统规划设计的重要环节[4]。作为生产辅助设施,单元上料口与下料口 (pickup/drop-off point, P/D 口) 布局是一类特殊的设施布局问题,负责生产设备的上料与下料作业,其位置布局是否合理直接影响车间物流的走向,将对控制车间物流成本起到重要作用。此外P/D 口作为缓冲区,在生产能力与物料运输能力由于不确定因素造成的失衡时起到缓冲作用。
在P/D 口位置布局研究中,少数文献[5-6]单独研究P/D 口位置布局问题,大多数集中在设施、物流路径和P/D 口集成布局上[7-9]。Park 等[10]以最小化不同设施P/D 口间的直角线距离和为目标,研究不等面积设施布局问题 (UAFLP),但没有考虑实际MHS与P/D 口的密切联系。由于单元P/D 口沿物流通道放置,因此在P/D 口布局时有必要考虑FCMHS。Ahmadi-Javid 等[11]注意到MHS 在设施布局中的特殊地位,以最小化单环物流路径距离为目标,研究不等面积设施布局问题,其把物流路径距离作为设施布局的依据,未考虑P/D 口在MHS 中的重要作用,在实际工程中设施间的物料运输是通过P/D 口实现的。文献[12]研究具有有限物料储运能力的单元流水式车间单元P/D 口的位置布局问题,其将FCMHS 车间中因拥堵现象产生的额外运输成本考虑进平均总运输成本的目标函数中。
单元P/D 口是在制品等待加工或转运的缓冲区,其容量大小直接影响系统产能和生产周期,也直接关系到企业的投资成本。有关制造系统缓冲区容量配置优化的研究中,Smith[13]注意到MHS 的重要性,研究了系统内AGV 数量及缓冲区容量的联合优化。席少辉等[14]研究了具有物料批量储运的装配生产系统中缓冲区容量配置问题,在满足产出率约束条件下,通过优化缓冲区容量配置,最小化缓冲区投资成本。张惠煜等[15]针对具有研配工序的制造系统缓冲区容量配置问题,研究在生产周期和产出率约束下优化缓冲区的容量。
高产出率和按期交货是个性化定制生产企业追求的目标,反映了一个企业的核心竞争力。因此,为了充分体现个性化定制生产企业的核心竞争力,在制造系统布局设计与资源配置阶段,必须将产品的产出率和平均生产周期作为重要的系统性能指标。文献[12]和[15]在满足产品产出率以及平均生产周期约束前提下,分别研究了设施布局和资源配置的优化问题。
综上分析可知,大多数设施布局研究基于物流距离矩阵的运输成本优化,鲜有研究将实际MHS的有限能力考虑在内。有限能力包括缓冲区内有限的储位、小车的有限运载量、数量及运行速度等。FCMHS 车间内单元P/D 口位置布局和容量配置能够引起车间物流强度的变化,使车间发生拥堵现象进而产生各种等待成本,包括因拥堵导致的不可忽略的额外成本,直接影响车间运输成本。现有文献较少见到将这类成本作为优化目标的一部分。同时,P/D 口容量配置直接影响到制造系统的性能,P/D 口容量太低会大大降低系统的产出率,太高则无法有效控制在制品的生产周期。最近的研究中暂未看到在FCMHS 单元流水式车间中,在满足产品产出率和在制品生产周期的预期能力要求下,同时优化P/D 口位置布局和容量配置的报道[16]。
为了解决FCMHS 单元流水式车间单元P/D 口位置布局与容量配置的联合优化问题,本文以最小化平均运输总成本和最小化P/D 口配置成本为多目标,建立具有产品产出率和在制品平均生产周期等车间性能指标约束的数学模型。针对问题的特点,提出一种嵌入自适应协同邻域搜索算法的网格自适应直接搜索算法 (ACNS-MADS),将所提算法应用到实际案例,与其他的算法优化结果进行对比分析。
1 P/D 口位置与容量的联合优化问题
1.1 问题描述
图1 为一种典型的单元流水式智能车间。假设单元流水式智能车间被划分成M个功能区块,每个区块内包含若干制造单元,车间内单元的数量为N,每个单元含有一个上料口 (P 口) 和下料口 (D 口),而且P 口与D 口的容量相同。在制品在区块之间以流水线生产方式移动,每道工序由对应功能区块内的任一并行制造单元处理,在制品在单元内加工完成后由物料搬运AGV 运往下一工序的任一单元内处理。车间内AGV 的数量是固定的。由于物流通道和对应的单元边界的双重约束,将每个单元P/D 口位置限制在若干备选位置上。为了保证车间的性能,将每个P/D 口的容量限制在合理范围内。为了提高企业的核心竞争力,P/D 口位置布局与容量配置方案必须满足系统对产品产出率和生产周期的要求。
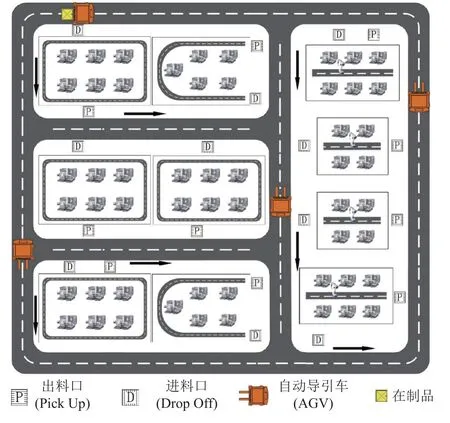
图1 一种典型的含P/D 口单元流水式智能车间Figure 1 A typical intelligent cellar flowshop with P/D points
本文的研究目标是在满足产品产出率和在制品平均生产周期的条件下,通过优化FCMHS 车间内各单元P/D 口位置布局与容量配置方案,使车间运输总成本和P/D 口配置成本达到总体的最优。
1.2 数学模型
根据以上问题描述,决策变量为x和 δ ,分别表示单元P/D 口的容量向量和位置向量。针对问题建立的数学模型中设计的参数符号定义如表1 所示。

表1 数学模型参数Table 1 Parameters of the model
本文以最小化车间平均总运输成本E{Q(x,δ)} 和最小化P/D 口容量配置成本C为优化目标,建立多目标混合整数规划模型。
其中,目标函数 (1) 为最小化平均总运输成本,包括AGV 负载与空载运行成本Q1(x,δ) 、在制品等待运输成本Q2(x,δ) 及因拥堵导致的运输成本Q3(x,δ) ;目标函数 (2) 为最小化P/D 口容量配置成本,成本向量c=[c1,c2,···,cN] , 容量向量 δ =[δ1,δ2,···,δN] 。
约束 (3) 为单元P/D 口位置约束,受单元所在车间空间的影响,将P/D 口位置xk限制在若干可选位置Pk上;约束 (4) 为P/D 口容量取值约束,P/D口容量太高或太低都影响车间性能,P/D 口容量δk需要限制在已知合理预期范围内Mk;约束 (5) 和约束 (6) 是车间性能指标约束,分别表示产品平均产出率E{Θ} 不能低于预期的下限值和平均生产周期E{T} 不超过预期的上限值,而 Θ 和T受车间中P/D 口位置x及容量 δ 影响,是关于x和 δ 的函数。
1.3 问题分析与解决思路
1.3.1 问题分析
该问题具有以下特点。
1) 考虑FCMHS 车间不可忽略的拥堵现象,在系统预期产能要求下,P/D 口联合方案必须满足产品产出率和在制品平均生产周期的要求。
2) P/D 口位置影响车间物流强度的分布,其容量不仅会影响物流强度,也会影响P/D 口配置成本。在进行P/D 口位置与容量的优化时,同时考虑物料运输成本与缓冲区配置成本。
3) 将FCMHS 车间拥堵成本作为车间平均运输成本的一部分,将产品产出率及在制品平均生产周期等预期性能指标作为约束条件之一,属于随机混合整数非线性规划模型。
上述特点为问题的求解带来以下困难。
1) 该问题由于拥堵成本、产出率和平均生产周期等系统性能指标无法采用封闭的数学形式表达,这为大量性能指标的计算带来了困难。
2) 单元流水式车间内工序间P 口与D 口数量达到平衡才能降低在制品的等待成本,同时对P/D 口位置与容量进行协同优化,才能使整体优化效果最优。如何协同P/D 口位置与容量的优化以及平衡工序间P/D 口容量,使总运输成本最小化的同时有较低的配置成本,也是本问题的困难所在。
3) 对于传统的非线性规划模型,一般采用基于函数的梯度信息获得寻优方向来求解[17],但由于无法获得目标函数和约束函数关于连续变量的导数,因而无法采用传统的非线性优化方法求解,这为该多目标优化问题的解决带来了困难。
1.3.2 解决思路
求解上述模型的关键在于计算系统性能指标,对于结构复杂的系统,难以获得精确结果或者存在维数灾难问题,一般采用近似解法和仿真法。近似解法在部分假设的基础上进行数学建模,无法充分反应复杂系统中的实际问题,而且上述模型中包含的性能指标无法采用决策变量的封闭数学表达式描述。在FCMHS 单元流水式车间中由于随机因素的影响导致的物流强度随时空间的变化而变化,拥堵漂移现象一直在发生。采用仿真法可以得到比较精确的性能指标值,获得系统中详细的仿真运行过程信息,有助于算法的求解。因此本文采用计算机仿真法计算系统性能指标值和获取仿真问题信息。
本文的优化目标包含平均运输总成本及P/D 口配置成本,前者反映企业中长期运营成本,后者反映生产活动前期的投资成本。从长远角度看,P/D口配置成本只在短期内对生产经营产生影响,而车间的平均总运输成本对控制企业的运营成本起着重要作用,在进行规划设计决策时应该作为主要决策因素。采用加权法为每个目标函数赋予权重因子,将多目标规划问题转化为单目标的优化问题进行求解。
从理论上讲,单元P/D 口可布置在单元边界上任意位置,但连续的位置变量给问题求解带来了困难,而单元边界处由于路径网络的约束以及不同的加工单元形状,在实际设施布局中只有有限的P/D口位置可选方案,可将P/D 口位置连续变量离散化,把模型转化成可求解的随机整数非线性规划模型[18]。通过离散化P/D 口变量后,大大减少了搜索空间,虽然随着单元数量的增多而呈现指数级增长,但近似求解仍然是可行的。
针对单元流水式车间中工序间P 口与D 口数量的平衡以及P/D 口位置与容量协同优化的求解难点,本文基于自适应问题信息集和随机邻域搜索,提出一种自适应协同邻域搜索法 (adaptive collaborative neighborhood search, ACNS)。将ACNS 算法嵌入网格自适应直接搜索算法 (mesh adaptive direct search, MADS) 中,求解单元P/D 口位置布局与容量配置的联合优化问题。
2 优化算法
2.1 编码方案说明
在开始算法之前,首先设计合适的编码与对应的解码。本文所研究问题是确定单元P/D 口的位置及其容量,因此一个完整的编码方案由两部分组成:一是各单元的P/D 口位置,单元P/D 口位置方案受车间内物理空间限制,有2 ~ 12 种不同P/D 口可选位置[12],故采用十六进制表示各个P/D 口位置方案,每一个数字 (1 ~ C) 表示一个P/D 口方案;二是各单元P/D 口的容量,同样采用十六进制表示各单元P/D 口容量,数字大小表示P/D 口最大容量,同一个单元的P 口和D 口容量相同。编码的长度为两倍单元数,将编码中的基本单位称为基因。
每个基因编号表示一个单元,编号相同但位置不同的两个基因属于同一个单元的P/D 口位置基因和容量基因。含有5 个单元的P/D 口位置与容量方案编码如图2 所示。前5 个基因为P/D 口位置编码“626C3”,表示各单元P/D 口位置方案;后5 个则为P/D 口容量“44352”,表示各单元P/D 口的最大容量。单元编号为1 的P/D 口位置和容量方案分别为“6”和“4”,其余单元以此类推。

图2 编码方案示意图Figure 2 Encoding diagram of a solution
仿真平台预设了P/D 口位置和容量的参数化设置,通过对编码方案进行解码,得到对应的仿真模型,仿真实验结束后将得到的目标函数值和问题信息返回算法平台,进行下一次迭代。以上述示意图为例,算法程序将P/D 口位置与容量方案编码“626C344352”传递到参数化仿真平台上,仿真平台根据接收的编码分别对P/D 口位置和容量进行参数设置,得到参数化的仿真模型。
2.2 ACNS-MADS 算法
2.2.1 ACNS 算法
如前所述,想要获得较好的方案,需要考虑P/D 口位置布局与容量配置的协同优化,以及区块(工序) 之间的P 口与D 口的容量达到平衡,在达到总运输成本最小化的同时有较低的P/D 口配置成本。针对以上特点与难点,首先需要一种提高P/D 口位置布局与容量配置方案协同性的方法;其次针对当前解进行局部更细致的优化,可以得到质量更高的解;文献[12]通过利用问题信息大大提高算法效率,但算法搜索过程中可能出现更优的不存在于问题信息集中的方案,也可能重复出现某些较优方案,因此可利用搜索过程中的信息,提高问题信息集的自适应性,加强算法搜索的方向性,提高算法效率。根据以上分析,本文提出的ACNS 算法能在当前解基础上有效协同P/D 口位置与容量的优化以及平衡工序间P/D 口容量,从而得到更好的P/D 口位置与容量联合方案。该算法包含3 种搜索方式。
1) 自适应性:定义自适应问题信息集,在每次算法迭代得到的结果中,利用问题信息集找到更优解时,把这个解对应的方案放进集合里,自适应调整集合内元素的出现概率。当利用问题信息集时,根据概率选择方案,可提高有效P/D 口布局方案的重用率。
2) 协同性:当算法搜索到新解后,新解可能不符合工序间P 口与D 口的容量平衡以及无法得到满意的P/D 口位置和容量联合方案,ACNS 算法的协同机制可对新解进行优化直至其满足P/D 口位置与容量约束。
其中,E为工序平衡度,表示使工序间物流顺畅的相邻工序P/D 口容量的最大差。
3) 邻域搜索: ACNS 算法是一种局部搜索方法,是在搜索到新解时,基于新解的邻域,对其进行进一步的优化。
通过自适应问题信息集根据方案出现的比例按概率进行邻域搜索得到新的P/D 口容量方案。搜索半径b为ACNS 算法中进行邻域搜索的半径。
2.2.2 ACNS-MADS 算法
本文针对单元P/D 口位置与容量的联合优化问题,提出一种嵌入ACNS 算法的网格自适应直接搜索算法 (ACNS-MADS)。该算法是基于MADS 算法[19]的扩展,延续了MADS 算法在局部最优化的同时也能兼顾全局优化的特点,而且在当前解的再优化时利用ACNS 算法寻找到更符合问题特征的解,从而提高解的质量和算法效率。ACNS-MADS算法在每次迭代过程中包含两个寻找新解的搜索步骤,分别是搜索步骤 (S 步) 和探测步骤 (P 步)。S 步在由离散决策变量组成的网格空间上 (一个网格表示一个可行解) 进行全局性的搜索,由于粒子群算法通过群体中个体之间的协作及信息共享进行寻优,具有良好的全局搜索能力,本文采用PSO 算法实现S 步搜索;P 步则在当前解附近一定范围内进行局部性的搜索,搜索方向和范围随着每次迭代而变化。而嵌入的ACNS 算法用于再优化初始解以及通过S 步和P 步得到的新解的P/D 口位置布局与容量配置。
初始解的选择对算法的效率有着极大的影响。本文针对所研究问题的特点,采用LHS 法[19]生成具有代表性的较合理的P/D 口位置与容量联合初始方案,为了生成符合问题特征的合理的P/D 口位置与容量联合初始方案,接着使用ACNS 算法对LHS解进行优化,得到的解记为 L HSA初始解。
2.3 算法流程
2.3.1 ACNS 算法流程
针对该约束最优化问题,采用罚函数法求解E{Q} 的极小点。定义罚函数fΩ(x) 为
其中,fΩ(x) 为 可行域 Ω 内关于联合优化方案x的平均运输总成本E{Q} 和P/D 口配置成本C的加权和;W1和W2分 别为E{Q} 和C的权重因子。若搜索到的解在 Ω 外,则赋予其足够大的惩罚值,那么该罚函数在 Ω 内可求得问题的解。
ACNS 算法具体步骤如下。
令A={a1,a2,···,ar} 为有固定布局方案的单元集,B={b1,b2,···,bs} 为根据问题信息需要优化布局的 单 元 集,r+s=M;记lak={akt} 为 单 元ak(k∈r) 的布局方案集合,lbk={bkt} 为 单元bk(k∈s) 的自适应问题信息集。 P I[k] 表 示单元k的P/D 口方案问题信息集,x′[k] 表 示单元k的P/D 口方案。
步骤0 初始化
1) 种群大小N,初始问题信息集 P I0,单元数M,搜索半径b,工序数T。
2) 初始化种群X={x1,x2,···,xN} ,自适应问题信息集 P I=PI0。
步骤1 自适应协同邻域搜索
3) 对于xi∈X,对于k∈M,有
其中,bkt根据集合 P I[k] 各单元P/D 口方案所占比例获得,则有P/D 口位置方案为
4) 随机邻域搜索优化P/D 口容量为
平衡P/D 口之间容量:对于任意工序Sτ, 1≤τ≤T ,如果满足
则得到P/D 口容量方案为
否则,重新执行 (4)。

步骤2 更新问题信息集和种群

否则,返回步骤1。
2.3.2 ACNS-MADS 算法流程
ACNS-MADS 算法具体步骤如下。
步骤0 初始化
网 格 大 小 参 数 δk,框 大 小 参 数 Δk, Δk≥δk>0 ,初始化迭代器k=0 ;种群n,终止条件 ε =1 。
步骤1 生成LHS*初始解
1) LHS 法生成初始种群x0={x1,x2,···,xn} 。
2) ACNS算法得到 L HSA解以及fΩ(x0)←minfΩ(xA)。
步骤2 S 步搜索:嵌入PSO 算法
3) 嵌入PSO 进行搜索得到该问题的非劣解t。
4) 若fΩ(t)<fΩ(xk),则利用ACNS 算法,获取t′及fΩ(t′) ;那么,xk+1←min(fΩ(t),fΩ(t′)) , Δk+1←Δk+1 ,执行步骤4;否则,执行步骤3。
步骤3 P 步搜索:MADS 算法

图3 为嵌入ACNS 的ACNS-MADS 算法流程图。
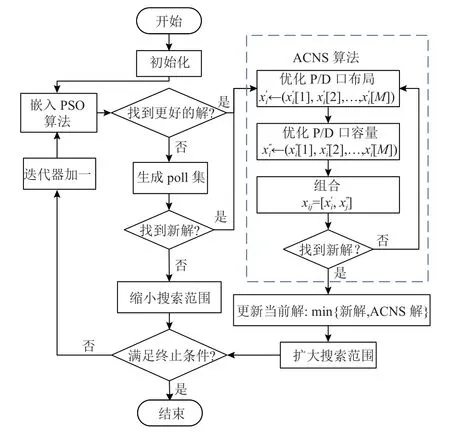
图3 ACNS-MADS 算法流程Figure 3 The flow chart of ACNS-MADS algorithm
3 案例应用与结果分析
3.1 案例背景
以某定制化制造企业新工厂规划设计项目为案例背景,使用本文所提ACNS-MADS 算法解决新工厂内车间单元P/D 口位置布局和容量配置问题。新工厂考虑原生产线的重新布局与新产品的产线布局,需要分别对不同的生产车间进行规划设计。该企业生产典型的多品种、小批量、个性化产品,由于生产设备的功能高度集成,新工厂使用由多个含机器人的柔性生产单元组成的车间,车间内物料大致沿着相同的流动方向,即单元式流水车间。在该项目的规划设计中,车间物流路径已规划完成,确定了单元区块的划分及区块相对位置,各区块内的制造单元数量以及尺寸、方向也已确定。现有4个车间,分别是 (3,3,3,3) 、 (2,3,4,4) 、 (3,2,2,4,3) 、(3,3,3,2,4),其中的数字个数代表车间内功能区块数,数值代表各个区块内单元的数量。对4 个车间的单元P/D 口进行位置布局和容量配置,使该新工厂既能达到原产线的产能要求,又能满足新产线的预期产能要求。
受车间建筑结构、生产和运输设备以及辅助生产区域 (如办公区、休息区、模具区等) 的限制,单元流水式车间内将形成不规则形状的生产区域,由此形成复杂不规则的物料运输网络。这就使得各单元的P/D 口布局问题复杂化,因此车间各单元的P/D 口分别有2 ~ 12 种不等的可选布局方案。另外,因为订单到达的不确定性以及产品工艺的差异性,P/D 口的位置布局决定了车间的物流强度,而P/D 口容量则决定了车间的生产效率。P/D 口容量太小,则影响产品的产出率;P/D 口容量太大,则影响产品的交货期。为此使用本文所提ACNSMADS 算法解决新工厂车间单元P/D 口位置布局及其容量配置问题。应用案例的具体系统参数如表2所示。
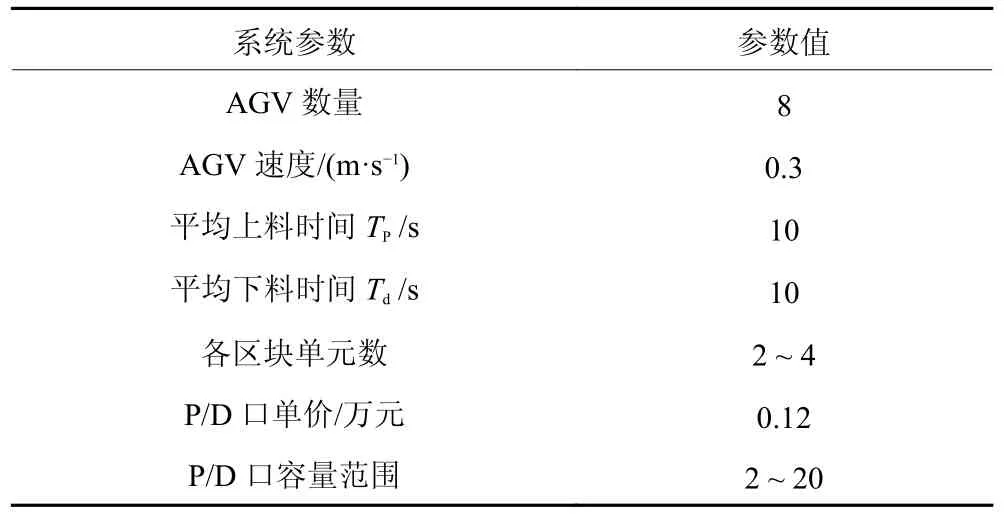
表2 应用案例的系统参数Table 2 System parameters of cases
3.2 对比算法的选取
本文选取嵌入GA 或PSO 的MADS 算法和几种常见的智能算法作为ACNS-MADS 的对比算法,通过算法应用的比较与分析,验证本文所提ACNSMADS 算法在优化车间单元P/D 口的位置布局及其容量配置问题的有效性及优越性。利用问题信息能够明显加快算法收敛速度,所以各个对比算法也都分为无利用问题信息和有利用问题信息进行实验。为了表示方便,列出各个算法的简称。各对比算法及其说明如表3 所示。
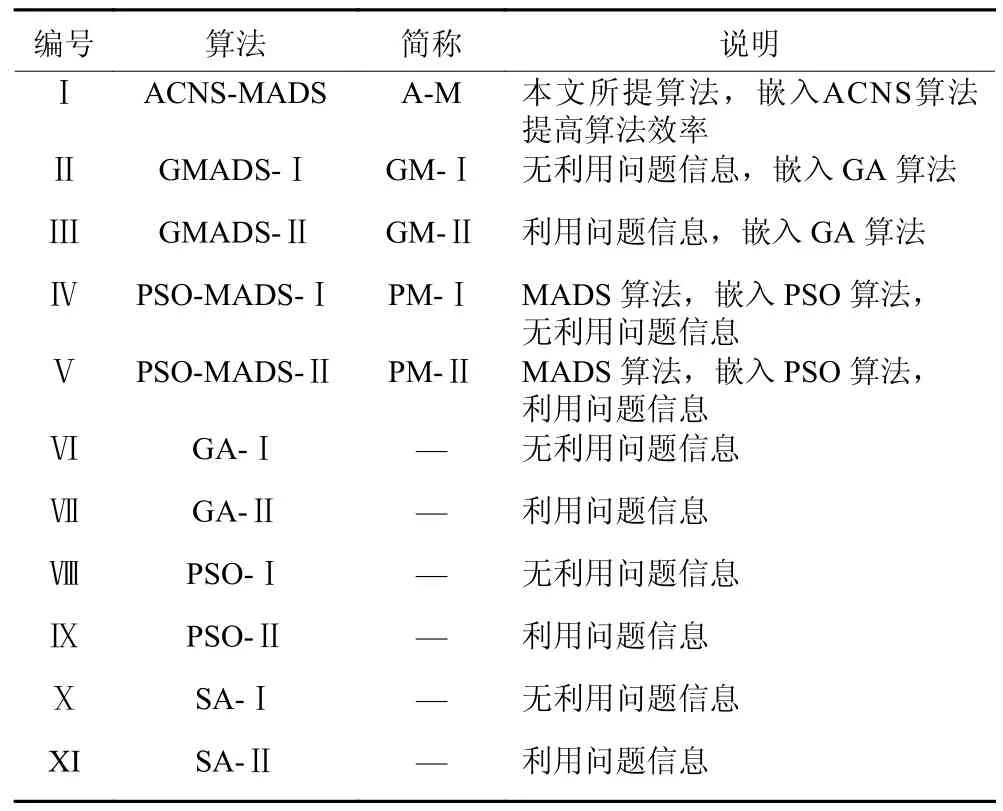
表3 算法特点对比Table 3 Comparisons of algorithms
3.3 案例结果与分析
优化算法部分在Matlab 平台上编程实现,仿真评估部分在Plant Simulation 仿真平台上建模实现,通过TCP/IP 通讯协议实现两个平台的数据通讯,数据包括优化获得的P/D 口位置布局方案与P/D 口容量方案,仿真获得的联合方案目标函数值、车间运行过程中的问题信息分析结果等。案例实验在Intel (R) Core (TM) i7-8700 CPU @ 3.20GHz,16.0 GB RAM 系统配置下进行。案例的实验结果如表4所示,表中E{Q}、C、T、TST、N分别表示平均运输总成本 (h/d)、P/D 口配置成本 (万元)、算法运行时间 (h)、仿真平均用时 (min) 以及仿真评估次数。

表4 对比算法的案例优化结果Table 4 Optimization results of algorithms
为了直观地反映案例实验结果,将实验结果用折线图绘制出来,如图4 ~ 8 所示。从表4 可以知道,利用问题信息的算法在平均总运输成本上得到比无利用问题信息的算法更好的结果,而且也缩短了算法运行的时间,如图6 所示。这说明利用问题信息通过加强算法搜索的方向性,不仅有效加快算法搜索的速度,提高算法的搜索效率,而且问题信息的方向性能够使该算法在联合优化问题上得到质量更好的解。
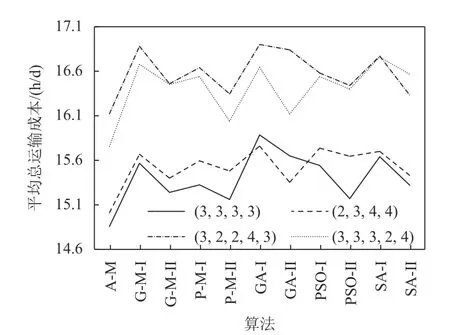
图4 平均总运输成本Figure 4 The average of total transportation cost
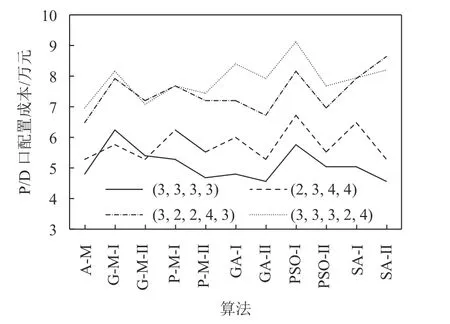
图5 P/D 口配置成本Figure 5 Allocation cost of P/D point
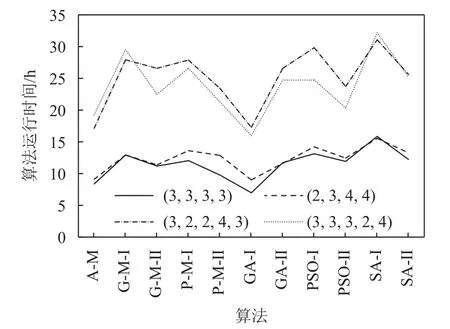
图6 算法运行时间Figure 6 Computation time of algorithms
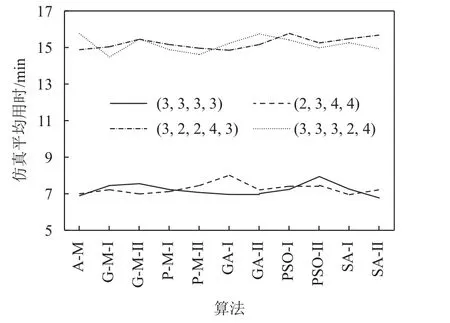
图7 仿真平均用时Figure 7 The average time of simulations
通过对比分析嵌入智能算法并且利用问题信息的G-M- Ⅱ和PM- Ⅱ算法以及ACNS-MADS 算法,可以知道ACNS-MADS 算法各项算法指标和性能指标有着更优的表现。如表4 所示,每个车间利用ACNS-MADS 得到的平均总运输成本与G-M- Ⅱ和PM- Ⅱ相比,降低了1.75% ~ 4.19%。这是因为ACNS算法利用自适应问题信息集,提高了解的质量,而且其协同优化能力使两个目标函数都达到了总体上的最优。在图6 中,ACNS-MADS 算法也具有相对较短的算法运行时间,相对G-M- Ⅱ和PM- Ⅱ缩短达10% ~ 36%。这是因为ACNS 算法优化的自适应性和协同性提高了算法的方向性,从而更快地得到优质的解。虽然ACNS 算法增加了仿真运行次数以及算法程序的运行时间。但如图8 所示,这也大大减少了ACNS-MADS 算法的总仿真评估次数,减少了算法运行的总时长。
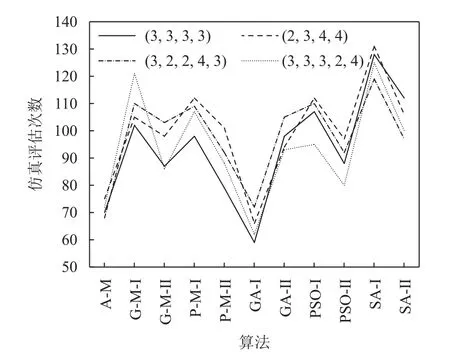
图8 仿真评估次数Figure 8 The number of simulation evalutions
通过图4 ~ 8 中GA、PSO、SA 等智能算法实验可以知道,由于部分算法容易陷入局部最优,算法过快收敛,导致解的质量不高。如图4、图6、图8中,GA- Ⅰ算法得到的方案呈现平均总运输成本高,算法运行时间短以及仿真评估次数少的特点,正是因为GA 算法极易收敛。在智能算法中引入问题信息后,加快了算法的搜索,但解的质量提高不明显,甚至会出现利用问题信息而得到的解中P/D 口配置成本反而增加的情况。如表4 所示,车间 (3,2,2,4,3) 和 (3,3,3,2,4) 出现SA- Ⅱ得到的P/D 口配置成本分别比SA- Ⅰ高9%和3%。而ACNS-MADS算法中引入自适应问题信息集,在搜索过程中问题信息集进行自适应调整,根据每次迭代搜索到的较优布局的频次按比例随机获取,出现频率高的方案将更容易出现,有效重复利用已搜索到的较好布局,大大提高了算法搜索效率和解的质量。因此相对于智能算法来说,ACNS-MADS 算法在效率和优度上具有明显的优势。
如图5 结果所示,PM- Ⅱ、GA- Ⅱ、SA- Ⅱ等算法获得的P/D 口配置成本不比ACNS-MADS 算法差,但从企业长期的经营来看,平均总运输成本是决定企业运营成本的关键指标,而P/D 口配置成本只在短期内对生产经营产生影响。在进行P/D 口的位置布局与容量配置的联合优化时,车间平均总运输成本应在最终决策时占据较大的权重。所以从短期看,PM- Ⅱ等算法能够得到局部较好的解,但从总体上和长期看,ACNS-MADS 算法得到的联合方案在获得最好的平均总运输成本时,也得到了较低的P/D 口配置成本,更优于其他算法。
综合以上分析,在求解单元P/D 口位置与容量的联合优化问题时,与其他算法相比,ACNS-MADS虽然部分指标 (如算法运行时间等) 不具有明显优势,但整体上看,仿真评估总次数平均少21%以上,算法时间平均减少17.95%以上,并且总运输成本和P/D 口配置成本分别减少2.99%和5.64%,ACNS-MADS 算法在效率和优度上具有明显的优势。ACNS-MADS 算法优于其他对比算法的原因在于嵌入MADS中的ACNS 算法有效地利用了自适应问题信息集,提高了较好的备选方案的重用率,加强了算法在搜索过程中的方向性,加快了算法收敛;同时,ACNS算法的协同优化机制有效地处理了P/D 口位置布局与容量配置的协同优化,使联合方案在获得最优的车间运输成本时 ,有效地降低了P/D 口的配置成本。因此ACNS-MADS 算法在求解单元P/D 口位置与容量的联合优化问题时比其他算法更优越,更有实用价值。
4 结论
本文研究P/D 口的位置布局与容量配置的联合优化问题,以最小化总运输成本和最小化P/D 口容量配置成本为目标,建立以平均产出率和在制品平均生产周期等系统性能指标为主要约束的数学模型。针对相邻功能区块P/D 口之间的耦合关系以及P/D 口位置与容量的协同优化的问题特征,提出嵌入自适应协同邻域搜索算法的网格自适应直接搜索算法 (ACNS-MADS)。以某制造企业新工厂规划实际为案例,使用所提算法求解P/D 口位置与容量的联合优化,并且与若干常见的算法优化结果进行对比和分析。案例实验对比结果表明,所提算法相比其他对比算法具有更好的性能,能够有效地解决智能制造车间规划设计阶段的单元P/D 口位置布局与容量配置。这说明了所提算法的有效性和求解该联合优化问题的高效性,所提算法具有一定的实际应用价值。
本文研究具有有限物料储运能力的单元流水式车间单元P/D 口位置布局与容量配置问题,不仅解决了制造系统规划设计阶段车间单元P/D 口位置布局设计以及容量配置设计问题,具有较高的实际应用价值,而且为具有有限物料储运能力的制造系统的设施布局与资源配置优化问题提供理论依据,填补了这一领域的空白。本研究具有以下创新点。
1) 研究考虑有限能力物料储运系统的单元流水式智能车间中同时进行P/D 口位置布局以及容量配置的联合优化问题。在该问题中,将FCMHS 车间中因拥堵而导致的成本作为优化目标的一部分。
2) 提出ACNS-MADS 算法求解单元P/D 口位置布局与容量配置的联合优化问题,其中ACNS 算法用于进一步优化求解不同工序P/D 口之间容量的耦合约束关系,从而得到质量更高的解。
由于算法初始解的优劣直接影响算法性能,后续工作将研究基于排队网的车间性能指标建模与分析,快速近似求解车间运行性能指标,通过MADS算法的优化获得质量较好的初始解。此外,单元内机器的布局直接影响单元P/D 口的可选位置,因此下一阶段的工作也将开展与P/D 口位置布局方案相对应的单元内机器布局优化。
