基于混合平衡优化器算法的多目标柔性作业车间多重动态调度研究
2023-11-22秦红斌孔仁杰常永顺李晨晓
秦红斌,孔仁杰,常永顺,李晨晓
(1.武汉理工大学 机电工程学院,湖北 武汉 430070;2.随州武汉理工大学工业研究院,湖北 随州,441300)
生产调度是智能制造中资源分配的核心,同时也反映了企业的生产效率,而在企业实际生产过程中,不可避免地会遇到紧急订单、机器故障和人为误操作等突发情况的影响,致使企业订单交货期延迟,生产效率骤降。相较于静态调度,动态调度能够针对不可预测的动态扰动下车间的实际生产情况,快速产生更具可操作性的决策方案,优化资源配置,平衡生产效率和交付绩效,降低库存,提高企业经济效益。因此对于制造业中广泛存在的多品种、小批量生产模式,研究柔性作业车间动态调度问题 (dynamic flexible job-shop scheduling problem,DFJSP) 具有重要的现实意义。
很多学者对DFJSP 展开过相关研究。如Baykasolu等[1]提出一种构造性算法,该算法采用贪婪的随机自适应搜索过程,能够求解具有机器容量约束和序列相关调整时间的柔性作业车间调度问题 (flexible job-shop scheduling problem, FJSP) 和DFJSP。Chen等[2]提出一种混合重调度策略以应对FJSP 中的随机机器故障情况,并以最大完工时间和机器总能耗为目标,采用NSGA-II 算法对构建的模型进行求解。Nie 等[3]提出一种解决机器故障干扰下的最小化离散制造车间生产总成本和碳排放的低碳动态调度优化方法。Mou 等[4]求解DFJSP 将遗传算法与自适应局部搜索相结合,并提出一种新的十进制编码方法。Zhang 等[5]提出一种改进的启发式Kalman 算法,其在该算法中结合边界处理函数,记录每个个体的最佳位置,构建细胞邻居网络,引入基于相对位置指数的编码方法,使改进的启发式Kalman 算法能够应用于求解DFJSP。
综上所述,现阶段对于动态调度的研究大多数是考虑单个扰动因素影响,对于多扰动因素作用下的DFJSP 研究还较少,且暂无综合有效性、快速性和稳定性的算法应对此类问题。针对紧急订单、机器故障这两类现实生产过程中最常见的突发情况,本文将二者结合考虑,研究了双重扰动影响下的DFJSP,并以最大完工时间、拖期惩罚及碳排放作为优化目标,建立多目标柔性作业车间多重动态调度模型。针对模型特点,本文设计了一种混合平衡优化器算法来求解该模型,进一步提高算法解决动态调度问题的有效性、快速性和稳定性。
1 问题描述与模型建立
1.1 参数设置
参数设置见表1。

表1 参数设置Table 1 Parameter settings
1.2 问题描述
本文研究双重扰动影响下的DFJSP,多重DFJSP可以描述为:车间中有可用机器集M={M1,M2,M3, ··· ,Mm} 来表示的m台机器,可用于加工不同工序;静态生产计划中有可用工件集J= {J1,J2,J3, ··· ,Jn} 来表示的n件工件待生产。每件工件的生产工序和工序数都已经预先固定且不可更改,不同工件间的生产工序和工序数允许不同。每道工序可以在给定的机器集中自由选择机器,相同工序在不同机器上和不同工序在相同机器上的加工时间和能耗均不相同。在Tro时刻,发生紧急订单事件,调度逻辑为Tro时刻前的静态调度不发生改变,Tro时刻后的调度方案根据紧急订单的订单截止时间进行第一重完全重调度;在Tdsm时刻,发生机器故障事件,此时故障机器上的加工工序立刻停止,等待机器修复后继续完成工序加工。调度逻辑和紧急订单事件相同,Tdsm时刻前的调度不发生改变,从Tdsm时刻开始,之后的工序进行第二重完全重调度。静态调度经过双重重调度后生成最终的调度方案。
1.3 动态调度策略分析
柔性作业车间的动态调度策略[6]一般可以分为基于事件的动态调度策略、基于周期的动态调度策略和基于事件和周期的混合动态调度策略3 种。此外,除了需要确定动态调度策略外,还需要确定重调度的具体策略,常见的有插入重调度和完全重调度两种重调度策略。
本文针对多重动态调度的特殊性,采用基于事件和周期的混合动态调度策略,重调度策略则采用完全重调度更为合适。
1.4 模型构建
本文研究基于紧急订单和机器故障双重扰动情况下的DFJSP,建立以最小化最大完工时间、最大拖期惩罚及最大碳排放为目标的模型。为便于研究,本文所设计的模型需在遵循如下条件假设下进行构建。
1) 零时刻所有机器均处于等待加工的状态。
2) 生产过程中物料充足,不考虑物料短缺情况。
3) 每台机器加工完一道工序后立即进入到下一道工序的加工,不考虑工件的准备与装夹时间。
4) 每台机器同一时刻只能加工一个工件。
5) 紧急订单事件发生后,为紧急订单设立高级别的拖期惩罚系数。Tro时刻前的调度不发生改变,Tro时刻后的调度进行第一重完全重调度。
6) 机器故障发生时,故障机器上的工序立刻停止加工,等待机器故障修复后继续加工,Tdsm时刻前的调度不发生改变,Tdsm时刻后的工序进行第二重完全重调度。
7) 只考虑机器在加工阶段产生的碳排放。
目标函数如下。
1) 最小化最大完工时间。
2) 最小化最大订单拖期惩罚。
3) 最小化最大碳排放。
约束条件为
式 (5) 表示生产涉及的工件物料充足,能够满足生产需求;式 (6) 表示同一工件不能出现加工时间存在重叠的工序;式 (7) 表示工件的工序之间存在先后顺序。
2 混合平衡优化器算法求解DFJSP
2.1 平衡优化器算法介绍
Faramarzi 等[7]于2020 年提出的平衡优化器算法 (equilibrium optimizer,EO) 是一种新型启发式算法,相较于传统遗传算法,在多样性和收敛速度上均具有较大优势。
大多数算法在迭代初期,所有个体没有一个引导的方向,只有最优个体确定后,其余个体才以某一种模式进行移动,EO 算法选择适应度排名前4 位的个体,并取四者平均值作为“第五人”,五者共同构成平衡优化池,在后续迭代更新种群过程中以同等概率在平衡优化池中随机选择一者引导其余个体,一定程度上避免了算法陷入局部最优。
式 (8) 表示平衡优化池,前4 个参数为种群中最好的4 个个体,第5 个参数表示前4 个个体的均值。式 (9) 主要影响种群更新规则,在算法中充当平衡算法的全局搜索和局部搜索的作用,式中,α1为权重系数;e 表示自然常数;r、λ 均为[0,1]内的随机向量;t为表示迭代次数函数值,随迭代次数增加而减小。式 (10) 中,α2为权重系数; Iter 为当前迭代次数; Max_iter 为最大迭代次数。式 (11)中G0表示质量生成速率。式 (12) 中r1、r2均为[0,1]内的随机数; GCP 是控制种群偏移速率的参数;GP 为生产率,一般设置为0.5。
最终个体的位置按式 (13) 进行更新,式中,V在算法中表示容量,此处等于种群数量。
2.2 混合平衡优化器算法设计
2.2.1 编码与解码
在算法设计前期需要确定调度基因的编码和解码方式,由于DFJSP 中几乎每道工序都可以在多台机器上进行加工,但是约束规则规定,每道工序只能选择在一台机器上加工,所以编码方式需要确定好每道工序最终是在哪台机器上加工,因此本文的编码方式采用基于工序和机器的双层整数编码方式。以K= {Kp,Km}来表示问题的一个调度方案,其中Kp和Km对应工件工序排序和工序机器选择两个部分。
以表2 为例。该例中有3 个工件,10 台机器,每个工件的工序不一定相同,工件1 有3 道工序,工件2 有4 道工序,工件3 有3 道工序,此外,机器加工不同工序的加工时间不同。具体编码过程如下。

表2 DFJPS 编解码案例Table 2 A case of DFJPS encoding and decoding
步骤1 工件工序层编码。在工件工序层Kp中的元素表示工件编号,相同元素出现的次数对应该工件的工序。对应表2 数据可知Kp={3, 2, 2, 1, 3, 1,1, 2, 3, 2},其中,第8 个元素是2,且为第3 次出现,表示工件2 的第3 道工序p23。
步骤2 机器分配层编码。机器分配层Km中的元素与Kp中的元素对应,表示对应工件工序可选机器集中的索引号。由步骤1 结合表2 可知,p23的可选机器集M23={M4,M6,M7},可得Km={2, 1, 3, 2,2, 1, 3, 3, 2, 4},Km的第8 个元素是3,表示工件2 的第3 道工序p23在其可选机器集中索引号为3 的机器即M7上加工。
根据以上分析可以得到问题的一个调度方案:K={3, 2, 2, 1, 3, 1, 1, 2, 3, 2 | 2, 1, 3, 2, 2, 1, 3, 3, 2, 4},当对调度方案K进行解码时,Kp的解码是编码的逆操作,而Km的解码需要找到对应工件工序的机器集并取出相对应的加工机器。
2.2.2 基于精英反向学习的混合种群初始化策略
算法开始阶段需要生成初始种群,初始种群在很大程度上决定了最终调度方案的质量。一般种群初始化采用随机初始化策略,随机初始化策略提高了解的全局性,缺点是往往会使得解的质量难以预测,影响种群的收敛速度。
反向学习的种群初始化策略[8]在很大程度上提高了种群的收敛速度,缺点是容易导致种群陷入局部最优。
综合以上分析,本文使用随机初始化和精英反向学习种群初始化结合的混合初始化种群策略,即70% 的个体采用随机初始化生成,30% 的个体采用精英反向学习初始化生成。这样既保证了种群的全局性和收敛速度,也避免了种群陷入局部最优。具体步骤如下。
步骤1 先随机初始化产生一个数量为nPop 的种群1 用Xs表示。
步骤2 计算Xs的适应度并排序,可以得到Xs的最优个体Xm和最差个体Xl,并将这两个个体从Xs中删除。
步骤3 再从Xs中随机选择数量为θf= nPop ×30%的个体,作为反向学习训练个体,用Xf表示。
式 (14) 中,Zfd表示反向学习的初始个体;η 为(0,1) 之间的随机数。个体Zfd经由修正后,再通过式 (15) 比较Zfd与Xfd的适应度值,选择适应度值较优的个体作为反向学习初始个体。
步骤4 随机产生数量为θs= nPop×70%的个体作为随机初始化个体,用Xs表示。
步骤5 整合随机初始化个体和精英反向学习初始化个体,得到X={Xs,Xf} 作为最终的初始种群。
2.2.3 引用Metropoils 准则的精英选择策略
算法迭代过程中,需要兼顾算法的全局搜索能力、局部搜索能力和收敛速度,因此在算法中引入结合Metropoils 准则的精英选择策略[9],在算法迭代初期,以较大概率保留较差的解,增大种群的多样性;在算法迭代后期,以较大概率保留较好的解,加快种群的收敛速度。
2.2.4 交叉和变异
为增加种群多样性,避免最终解集陷入局部最优,平衡优化器种群增加交叉和变异操作,因为种群初始化时使用的是基于工序和机器的双层编码,为避免产生非法解集,对工序层和机器层采用两种不同的交叉方式,即工序层使用IPOX 交叉方式[10],机器层采用MPX 多点交叉[11]。
本文在交叉过程后再增加变异操作,进一步提高种群多样性。采用随机变异[12]的方式,对染色体的工序层和机器层随机选择变异点进行变异。
2.2.5 变邻域搜索
邻域搜索[13]是提升算法局部搜索能力的强有效途径,由于本文采用的编码方式是双层编码,因此分别对工序层和机器层采用邻域搜索。
机器部分的邻域搜索是通过交换工序可选机器集内的机器实现的。
工序部分的变邻域搜索是通过交换工序实现,首先找到关键工序块,如图1 所示,有[101]、[201,302, 102, 202, 203]、[203, 103, 204]3 个 关 键 工 序块,由于[101]只有一个工序,不需要交换工序;[201, 302, 102, 202, 203]为中间工序块,块首的[201, 302]两道工序相互交换,块尾的[202, 303]两道工序相互交换;[203, 103, 204]为尾部工序块,交换[203, 103]两道工序。

图1 工序变邻域搜索Figure 1 Variable neighborhood searching of work processes
2.2.6 混合平衡优化器算法流程
混合平衡优化器算法 (hybrid equilibrium optimizer, HEO) 的算法流程如图2 所示,具体步骤如下。

图2 HEO 算法流程图Figure 2 The flowchart of the algorithm HEO
步骤1 设置算法参数,种群大小为150,算法迭代次数为200 次,变异率为0.3,交叉率为0.8,全局搜索权重参数1 为0.1,全局搜索权重参数2为0.3。
步骤2 初始化种群,30%的个体通过反向学习产生,70%的个体通过随机初始化产生。
步骤3 对种群进行非劣排序,进入种群迭代环节,取排序前4 的个体作为平衡优化池的个体,再对这4 个个体求和取均值,作为平衡优化池的最后一个个体。
步骤4 按式 (13) 更新种群,取更新后的30%个体生成交叉变异个体。
步骤5 取交叉变异个体和剩下的70%平衡优化器个体进行双重变邻域搜索,并采用Metropoils原则保留个体。
步骤6 整合种群。
步骤7 判断当前迭代次数是否小于设置的最大迭代次数,若小于,则重复步骤2 ~ 6;否则,算法结束,并取步骤6 生成的最终种群作为最后结果。
3 实验分析
3.1 拓展算例
仿真实验在Matlab (Matlab2020a) 语言环境下进行编程实现。
本篇论文选取标准测试算例Brandimarte[14]中FJSPmk 系列算例,综合多样性因素,选取FJSPmk01、FJSPmk02、···、FJSPmk15 共 计15 个 算 例 进 行 扩展。算例参数如表3 所示,其中加工时间、机器功率、交货期在一定范围内波动。
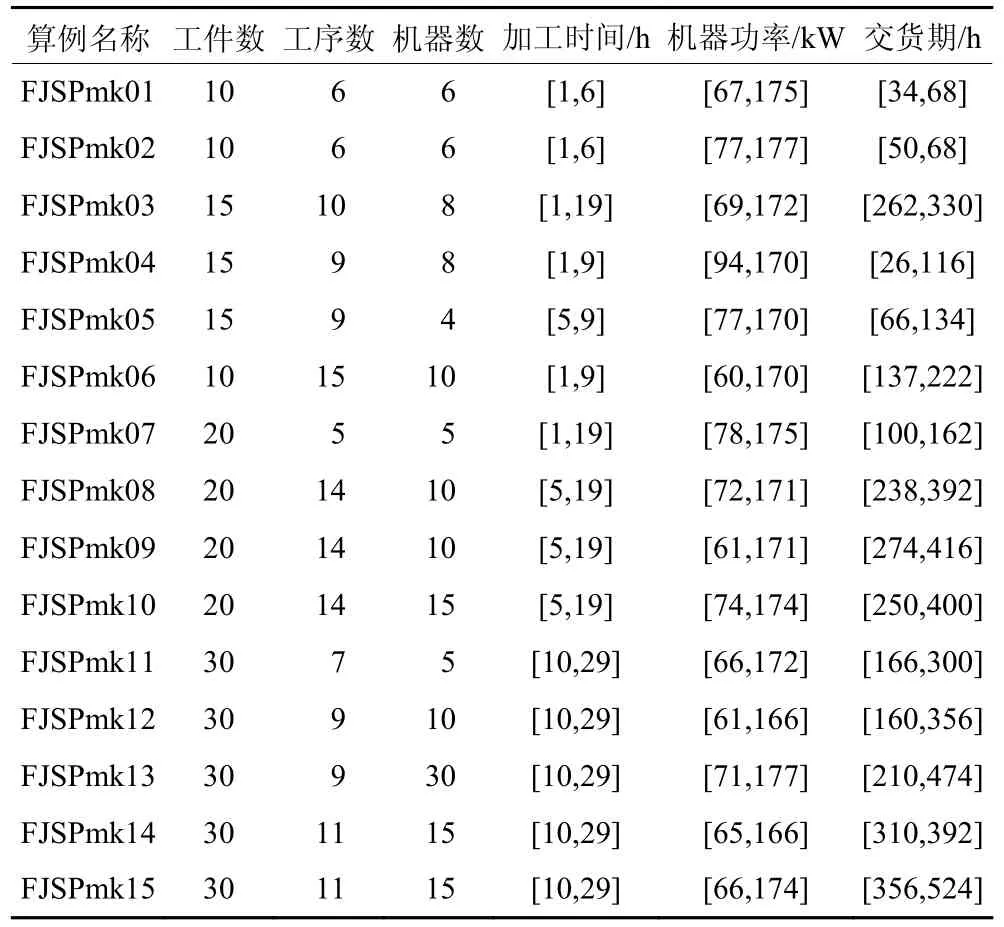
表3 算例参数Table 3 Parameters of numerical instances
根据表3 的算例参数,如表4 所示,进行紧急事件参数表拓展。
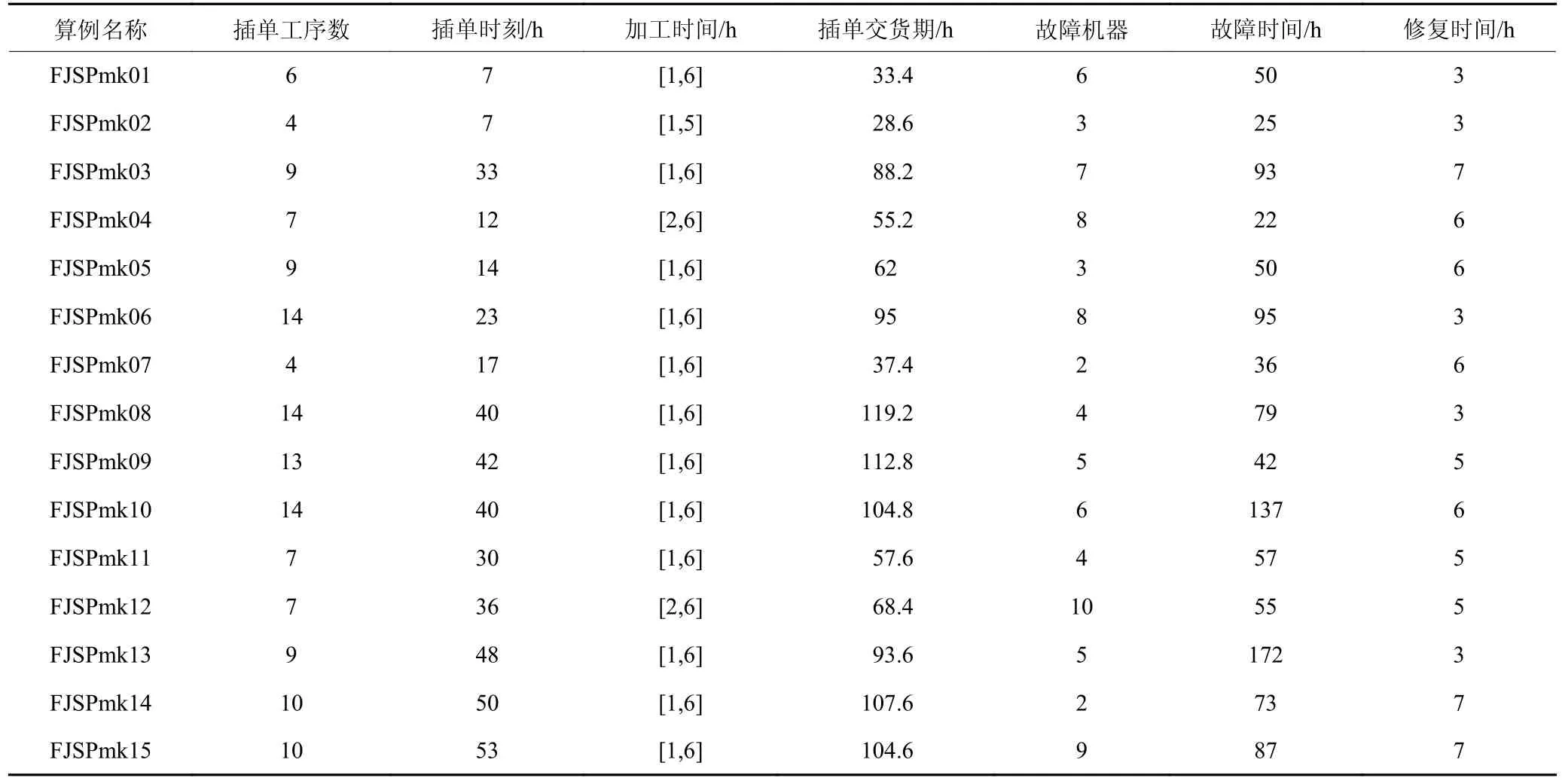
表4 紧急事件参数表Table 4 Parameters of emergency events
3.2 评价指标
多目标优化算法解集的性能评价指标可以主要分为收敛性评价指标、均匀性评价指标、广泛性评价指标3 类。这分别反映了解集与真实Pareto 解集之间的接近程度;解集中个体分布的均匀程度;解集在目标空间中分布的广泛程度。本文采用Cf (覆盖率) 指标、SP (空间) 指标和IGD (反转世代距离)指标对解集的均匀性、收敛性、多样性进行综合评价。
本文需要用到理论最优解集PF*定义如下。每个算法在每个算例上分别计算10 次,得到10 个Pareto前沿,将其合并成一个解集A,再取A的Pareto 前沿作为理论最优解集PF*。
各评价指标具体计算公式为
其中,A、B为两个算法的Pareto 解集;ε、β是解集A、B中任意一个解, ε ≻β 表示ε 支配β;分母|B|是解集B中解的个数; Cf (A,B) ∈[0,1],其值越大,表示A算法解集支配B算法解集的解个数越多。
其中,dmeq为两点之间的曼哈顿距离;S表示种群;|S|表示种群数目;xeq表示种群S中的第eq 个个体,且1≤eq≤|S|;xv表示种群S中除xeq外的任意一个个体;Fu表示种群S中某个体的目标函数值。SP 值越小,代表解集多样性越佳。
其中,dlel计算的是PF*中每一个解到S的最短欧氏距离;yel表示理论最优解集PF*中的第el 个个体解,1≤el≤|PF*|,|PF*|表示PF*中解的个数;x表示种群S中的任意一个个体。IGD 值越小,代表解集综合质量越好。
3.3 正交试验
对于HEO 算法,其中多数参数是随机变量,在固定范围内波动,因此需要确定参数最佳值。本文采用正交试验确定HEO 的参数最佳值,每个因素设置3 个水平,正交试验的参数设计见表5。
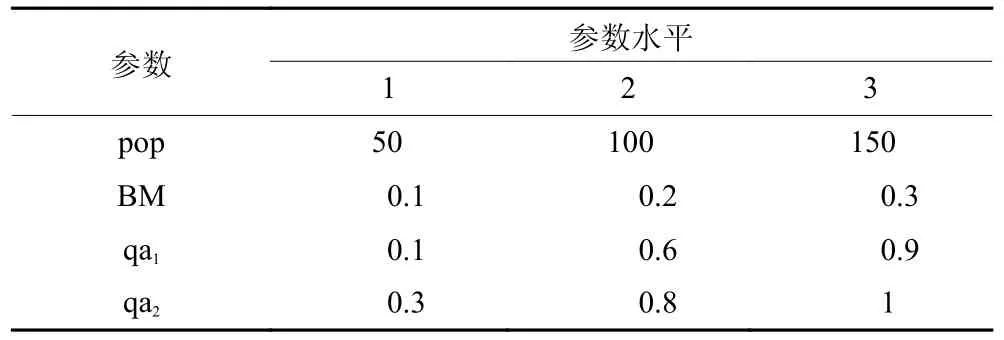
表5 正交试验参数Table 5 Parameters of orthogonal test
表5 中,pop 表示种群数量;BM 表示变异率;qa1表示全局搜索权重参数1;qa2表示全局搜索权重参数2。
由于本文的正交试验是基于三水平四因素,因此采用L9(34) 正交表。根据正交试验参数表,选用FJSPmk04 作为正交试验的主算例,使用HEO 更改相关参数值,每组参数值运行10 次,得到该组参数下的10 组不同解集,再将这10 组解集合并后取其Pareto 前沿,作为该组参数下的理论最优解集,选取解集的IGD 作为正交试验的综合评价指标。
根据表6 中的正交试验结果,可以得到各个因素取不同值,对IGD 值的影响程度。为更清楚观察实验结果,现将同因素3 个水平的IGD 值求和取均值,定义为该因素对算例的影响程度,可绘制如图3所示结果图。根据图3,可以看出当种群数量为150,变异率为0.3,全局搜索权重参数1 为0.1,全局搜索权重参数2 为0.3 时IGD 值最优,代表此组参数下算法的综合性能最好。
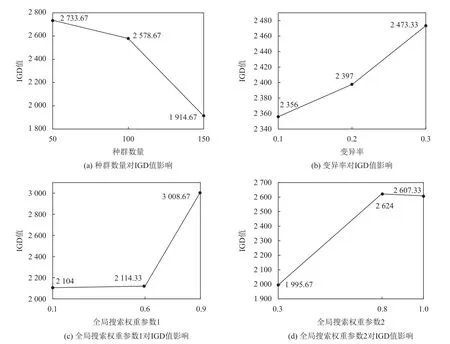
图3 参数变化图Figure 3 Parameter variations
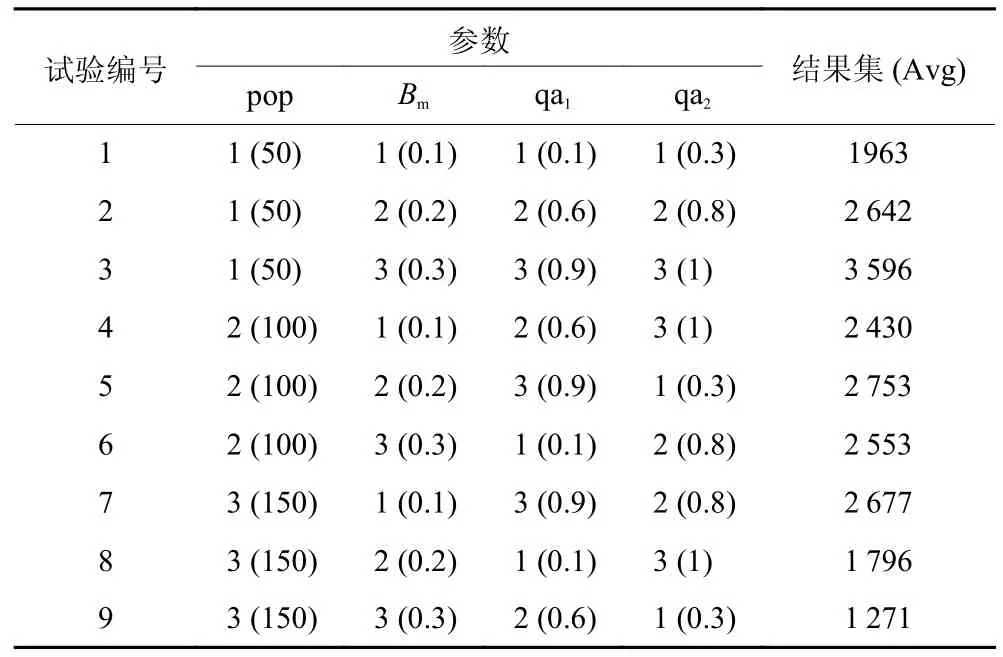
表6 正交试验结果集Table 6 Results of orthogonal test
所以本文将150、0.3、0.1、0.3 分别设置为HEO中种群数量、变异率、全局搜索权重参数1、全局搜索权重参数2 的参数值。
3.4 算法对比
3.4.1 各算法目标值对比
本 文 选 取MOPSO[15](A2) 、IGWO[16](A3) 、NSGA-II[17](A4) 和EO (A5) 4 种算法作为HEO (A1)的对比算法,EO 为HEO 未改进前的原算法。
通过对比HEO 和各算法的目标值结果,观察算法对各调度目标 (最小化最大完工时间F1、订单拖期惩罚F2、碳排放F3) 的影响情况。
实验分析部分共使用15 个拓展算例,5 种算法,每种算法对每个算例求解10 次,其中,每次运行迭代300 代,共需经过225 000 次运行获得最终实验数据。
由于篇幅限制,将15 个拓展算例的最终结果取均值,绘制柱状图如图4 所示。由图4 可知,EO 相较于其余对比算法,在各目标值求解中具有一定的优越性,此外,改进过后的HEO 对于3 个目标值的提升效果更为显著。
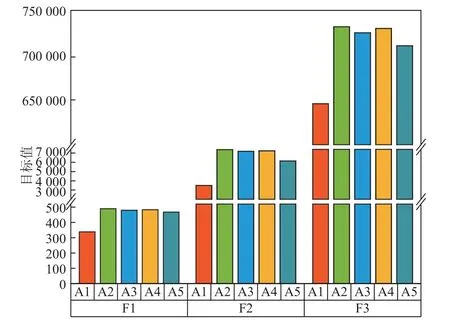
图4 各算法目标值对比Figure 4 Comparisons of objective values of each algorithm
3.4.2 算法对比
通过比较5 种算法在各个算例中运行所获得的最优解集质量来判断算法的优劣性。以Cf、SP、IGD作为算法的评价指标。
每种算法对每个算例求解10 次,最终的评价指标数据取10 次结果的平均值。
根据表7 的数据可以看出HEO 对于其他对比算法的Cf (覆盖率) 基本为1,说明HEO 在求解DFJSP时的收敛性明显强于其对比算法。

表7 各算法平均Cf 比较Table 7 Comparisons of the average Cf using differernt algorithms
根据表8 的试验结果可以得出,HEO 的 IGD(世代反转距离) 数值基本小于其他算法的数值,这说明HEO 的综合性能强于其他对比算法。由表9可知,在SP (空间指标) 上,HEO 的数值也大都小于其他对比算法,说明HEO 解集的多样性也强于其对比算法。因此HEO 在收敛性、多样性和综合性方面均表现优秀。
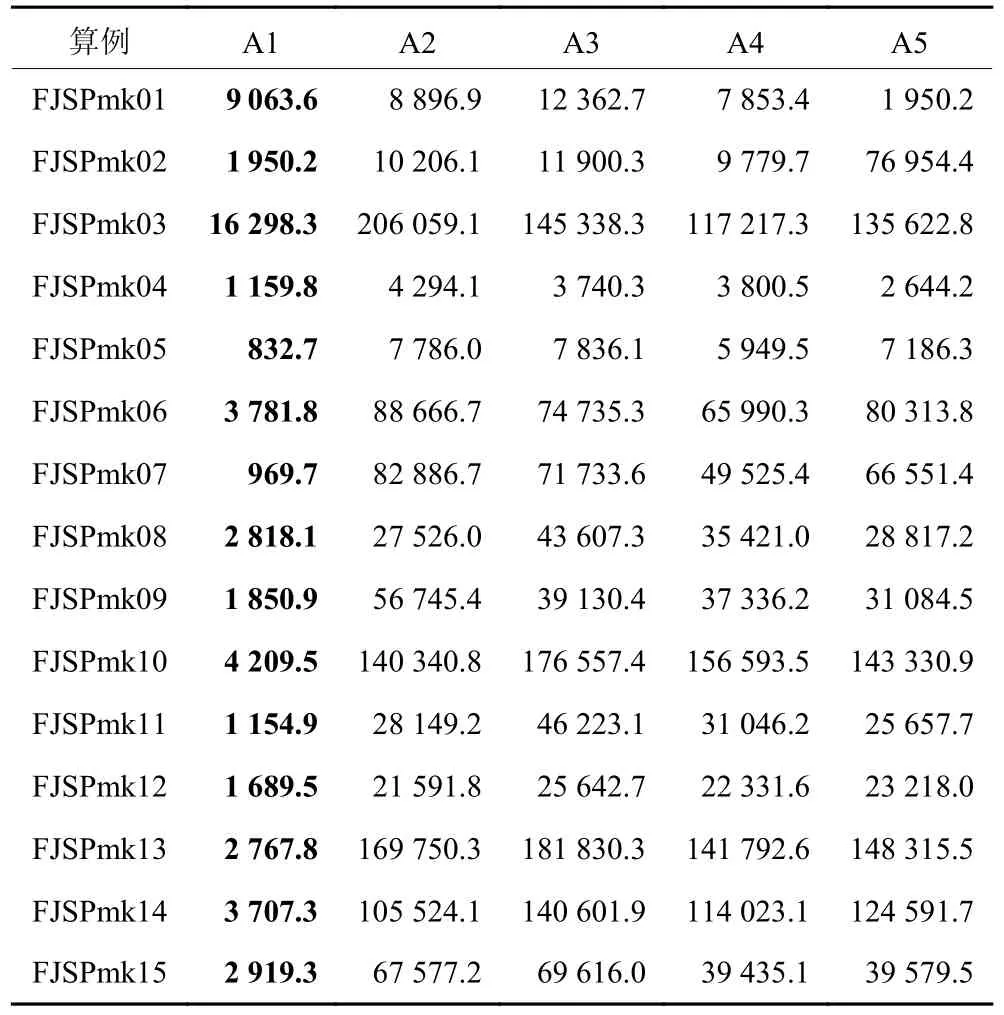
表8 各算法平均IGD 比较Table 8 Comparisons of the average IGD using different algorithms
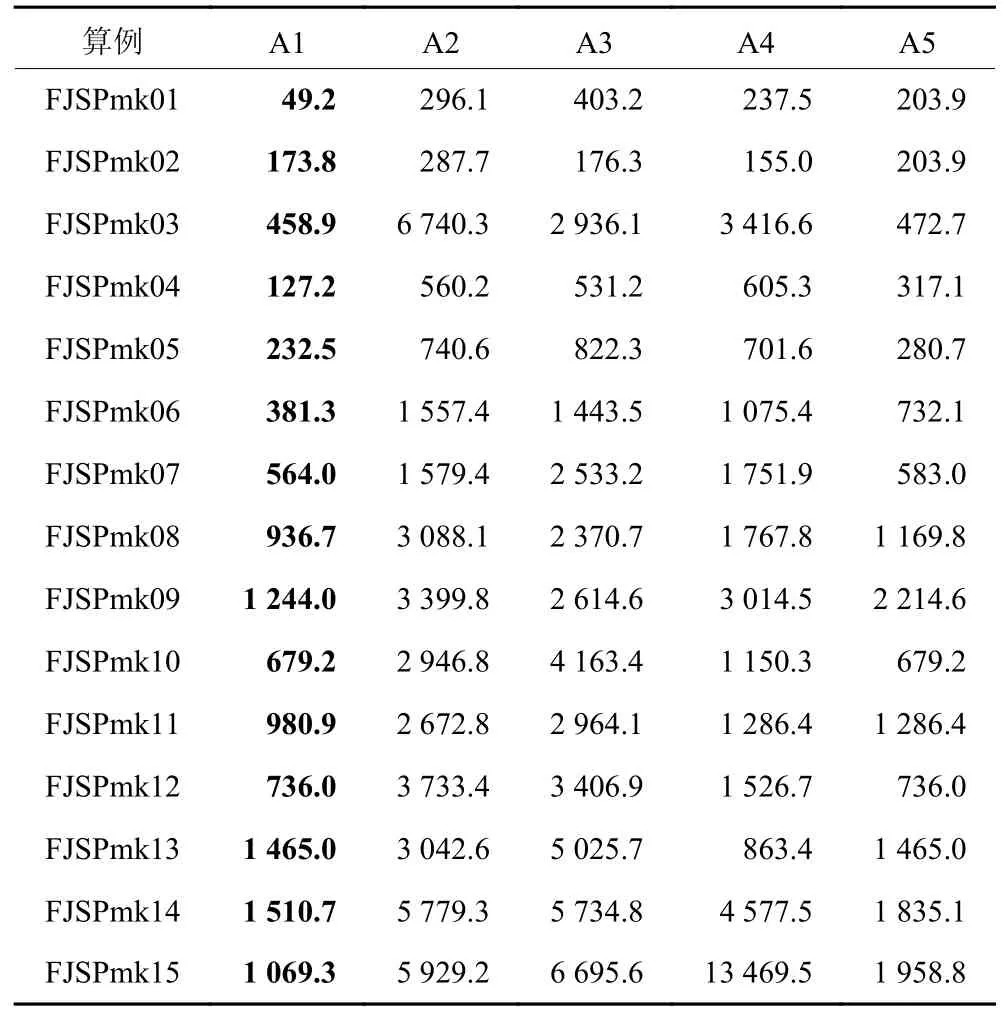
表9 各算法平均SP 比较Table 9 Comparisons of the average SP using different algorithms
本文以FJSPmk15 算例为例,以甘特图的形式展示使用HEO 求解该算例的最优调度方案。该算例共有30 个工件,每个工件最多含11 道工序,车间可供选择的机器有15 台。
双重动态调度甘特图如图5 所示,53 时刻发生紧急订单事件进行插单操作,93 时刻机器11 发生故障,机器上的23 号工件的第2 道工序立即停止,等待机器维修,在100 时刻时机器维修完毕,并继续进行加工,同时对后续的调度方案进行完全重调度,在455 时刻完成对插单工件的加工。
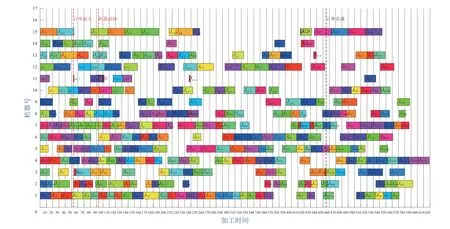
图5 双重动态调度甘特图Figure 5 The Gantt chart of dual dynamic scheduling
4 结束语
本文研究了基于混合平衡优化器算法的多目标DFJSP,根据问题定义,构建以机器故障和紧急订单为扰动因素,以最小化最大完工时间、最小化拖期惩罚和最小化碳排放为目标的DFJSP 模型,并提出一种混合平衡优化器算法。该算法在平衡优化器算法基础上增加基于精英反向学习的混合种群初始化策略,在提高初始种群质量的同时提高种群多样性;为平衡优化器子代增加交叉、变异和变邻域搜索操作,再通过精英选择策略来更新种群,平衡算法的全局搜索能力和局部搜索能力。通过大量拓展算例的仿真实验,验证了混合平衡优化器算法在求解动态柔性作业车间调度问题上的有效性、可靠性和优越性。
