基于HighD 数据集的高速公路交通冲突预测方法
2023-11-22揭文祺
揭文祺
(中国人民公安大学,北京 100038)
高速公路运输领域快速发展的同时,交通事故率也有所上升,加强高速公路行车安全研究有助于保障交通运输的安全性。以往交通安全研究大多以交通事故数据为基础,其中交通事故模型技术是传统交通安全研究的核心技术之一[1-4]。然而,受交通事故数据记录体系不完善等条件制约,事故记录数据一般与真实事故数据存在一定出入。此外,多数轻微事故数据通常不被记录,而这部分事故影响程度往往更能反映道路的行车安全水平。相关影响因素制约了传统交通安全研究的准确性及有效性[5]。
为解决这类问题,交通冲突技术在交通安全分析中得到广泛应用[6-11]。交通冲突数据具有大样本、短周期、小区域、高信度的统计学优点[5],并且基于交通冲突的交通安全研究能够弥补事后安全研究的短板。此外,研究表明交通冲突与交通事故之间存在稳定的相关性,可以有效反映所评价路段的行车安全水平[12-13]。由于交通冲突数据具有与交通事故数据相似的非负整数的性质,目前国内外的交通冲突预测模型大多参照交通事故预测模型建立,诸如线性及非线性回归模型[14-15]、广义线性模型[10,16]、零膨胀分布模型[8,11]、泊松-对数正态模型[17]、神经网络模型[18]等。然而这些模型研究大多未区分交通冲突的严重程度,无法很好地反映交通安全影响因素对冲突频率的影响。
随着计算机视觉和图像处理技术的发展,目前车辆自然轨迹数据集的获取已有许多是通过监控视频、无人机航拍、路测雷达等相关技术手段,诸如NGSIM(Next Generation Simulation,下一代仿真)数据集[1]、HighD 数据集[19]和同济道路轨迹数据平台等。其中,HighD 数据集使用先进的计算机视觉算法,定位误差通常<10 cm,可为研究人员提供准确的车辆轨迹、交通流指标以及交通冲突指标。
本研究基于HighD 数据集[19],根据TTC 的大小划分不同严重程度冲突的阈值,利用皮尔逊相关性分析筛选用于建模的关键影响因素,分别采用泊松模型、负二项模型、零膨胀负二项模型及零膨胀泊松模型进行回归分析,并根据评价指标确定不同严重程度的冲突最优模型,这有助于高速公路的主动安全防控,从而改善行车安全。
1 数据描述与处理
1.1 数据说明
HighD 数据集[19]源于2017—2018 年无人机拍摄记录的德国科隆附近6 个不同的地点数据,采用先进的计算机视觉算法从拍摄记录中提取车辆的行驶轨迹。这些轨迹数据及地点信息被分为60份,分别编号1~60。每份信息包含记录地点的高空照片、记录元信息、单车跟踪信息以及逐帧轨迹信息。本研究选取HighD 数据集路段1 方向1 的轨迹数据进行研究,从视频中共提取39 636 条小车数据以及7 640 条卡车数据。路段1 为双向6 车道,路段1 示意如图1 所示。其中车道6、车道7、车道8 的方向为方向1。HighD 数据集使用全球坐标系,坐标原点在图像左上方,因此方向1 中记录的车辆沿X轴速度为负,并且当加速度>0 时代表减速。

图1 路段1 示意
1.2 数据处理
1.2.1 交通流特征指标的提取
为便于分析,以1 min 为单位时间,将车辆轨迹信息分割为612 条数据。
通过每分钟的车辆逐帧轨迹信息提取1 min 内路段1 处的交通流参数,包括平均车头间距DHWm、平均行驶速度Vm、平均加速度am、车头间距标准差DHWs、行驶速度标准差Vs和加速度标准差as。值得注意的是,由于各车沿Y轴的速度与沿X轴的速度相比较小,可将沿X轴的车速近似看作车辆的行驶车速。其中,平均车头间距均值为47.226 m,车头间距标准差为8.843 m;平均行驶速度均值为28.236 m/s,行驶速度标准差为4.708 m/s;平均加速度均值为-0.135 m/s2,加速度标准差为0.121 m/s2。
车头间距计算指标的计算公式如式(1)所示。
式中,xi(t) 为车辆i在时刻t的位置。
1.2.2 交通量、变道率及货车率的提取
通过每5 min 的单车轨迹信息可得各时间段路段1 的流量以及货车流量和车辆变道次数,根据提取到的指标可以计算每分钟内路段1 的车辆变道率Plc和货车率Ptr,车辆变道率Plc计算公式如式(2)所示。
式中,numLanechangesi为每辆车轨迹信息所记录的车道变换次数;Qi为第i个1 min 内方向1 的交通量。
货车率Ptr计算公式如式(3)所示。
式中,numTrucksi为第i个1 min 内路段1 的货车交通量。
1.2.3 冲突事件的提取
为刻画冲突的严重程度,进一步对交通冲突指标进行划分,建立不同严重程度的冲突预测模型。同时建立总体的冲突模型并与其进行比较,探究不同交通流参数对冲突严重程度的影响。根据研究[20],将冲突划分为3 个程度:轻微冲突(3 s <TTC≤6 s)、一般冲突(1.5 s<TTC≤3 s)以及严重冲突(0 s<TTC≤1.5 s)。
行驶当前时刻下,后车速度大于前车,若两车保持原有的速度和行驶轨迹不变(即假定驾驶人不采取避险行为),根据当前速度和轨迹,将会在某个时刻发生碰撞,那么从冲突开始至碰撞发生的时间段即为TTC。TTCi的计算公式如式(4)所示,
式中,xi-1(t) 和xi(t) 分别为车辆i-1 与车辆i在t时刻的行车位置;vi-1(t) 和vi(t) 分别为车辆i-1 与车辆i在t时刻的瞬时车速;li-1为车辆i-1 的长度。TTC 为负值时代表当前车速下无冲突风险。
1.3 数据描述性统计
1.3.1 交通流特征指标描述
根据提取的交通流信息进行数据汇总,变量描述性统计如表1 所示。
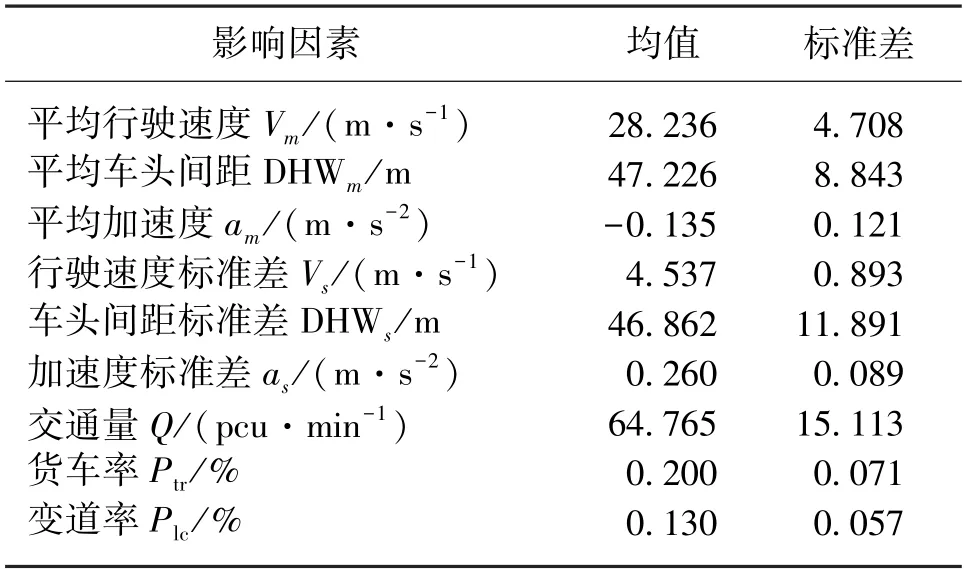
表1 变量描述性统计
1.3.2 交通流状态描述
根据所提取的各时段交通量和平均车辆行驶速度可以得到路段的车流密度D,计算公式如式(5)所示。
根据获得的密度和交通量可绘制路段1 的流量密度图,路段1 流量密度关系如图2 所示。分析可知,路段1 大多数时间段处于自由流状态,其处于不稳定状态(非饱和状态过渡至饱和状态)和拥堵状态下的时间段较少。

图2 路段1 流量密度关系
2 模型的建立与分析
2.1 计数模型建立
研究旨在对路段上单位时间内发生的交通冲突次数进行预测,而交通冲突次数属于非负计数数据,这类数据并不适用于线性回归建模。在冲突预测方面,常用的计数模型有泊松模型、负二项模型、零膨胀负二项模型、零膨胀泊松模型等。
若yi为第i个样本单位时间内发生的冲突次数,假设其服从参数为λ的泊松分布,则P(yi)的计算公式如式(6)所示。
式中,i=1,2,…,n(n为观测样本总数);P(yi)为第i个观测样本在单位时间内发生yi次冲突的概率;λi为第i个观测样本在单位时间内交通冲突次数的期望值。
λ通过连接函数g(·)与预测变量联系起来,对于服从泊松分布的因变量连接函数一般为自然对数,相应计算公式如式(7)所示。
式中,X1,X2,…,Xm为影响冲突个数的因素;β0,β1,…,βm为回归系数。
泊松分布的基础假设为服从泊松分布的计数变量的均值与方差相等,这导致泊松分布不能很好地解释交通冲突的离散性,因此可考虑在负二项模型中引入误差项εi,并对冲突数据的离散问题进行解释,计算公式如式(8)所示。
式中,exp(εi) 服从gamma(θ,θ)分布且均值和方差分别为1 和α。此时泊松模型可以拓展为负二项模型
式中,yi为第i个样本中方向1 上发生的交通冲突次数,Г(·)为伽马分布。
为处理计数数据中出现过多0 的情况,可以考虑引入零膨胀模型。零膨胀模型是二段式模型,由1 个二分类模型和1 个计数模型组成。零膨胀模型假设单位时间内的冲突次数有2 种可能状态:状态1 表示冲突次数为0,状态2 表示冲突次数依据计数模型分布。其中状态1 的概率假设为πi,那么状态2 发生的概率为1-πi,则零膨胀模型中单位时间冲突次数yi的概率分布可表示为
式中,g(yi) 为计数模型分布概率,通常为泊松模型或者负二项模型。
冲突次数处于状态1 和状态2 的概率,利用二元Logit 模型确定:
式中,WT为协方差向量的转置;γ为模型回归系数的向量。
2.2 影响因素共线性处理
根据相关性回归可以选择共线性较弱的影响因素进行回归分析,同时可以采用VIF(variance inflation factor,方差膨胀因子)检验法,一般认为VIF>10 时,该变量与其他变量之间存在较强的相关性。VIFi计算公式如式(12)所示。
式中,Ri为变量xi与其他因子xj(j=1,2,…,k;k≠j) 间的复相关系数。
2.3 模型选择准则
本研究采用AIC(Akaike Information Criterion,赤池信息量准则)、BIC(Bayesian Information Criterion,贝叶斯信息准则)对模型的拟合结果进行判定,以选择最合适的模型。AIC 和BIC 越小表示模型分析的效果越好,AIC 计算公式如式(13)所示,BIC 计算公式如式(14)所示。
式中,ln(L) 为似然函数;α为可估计的自由参数个数;n为样本例数。
3 冲突分析结果
3.1 初步分析
第一步,根据1.2.1 节中提取到的交通冲突信息绘制出不同严重程度冲突的频率分布直方图,3 种类型冲突次数的频数分布如图3 所示。
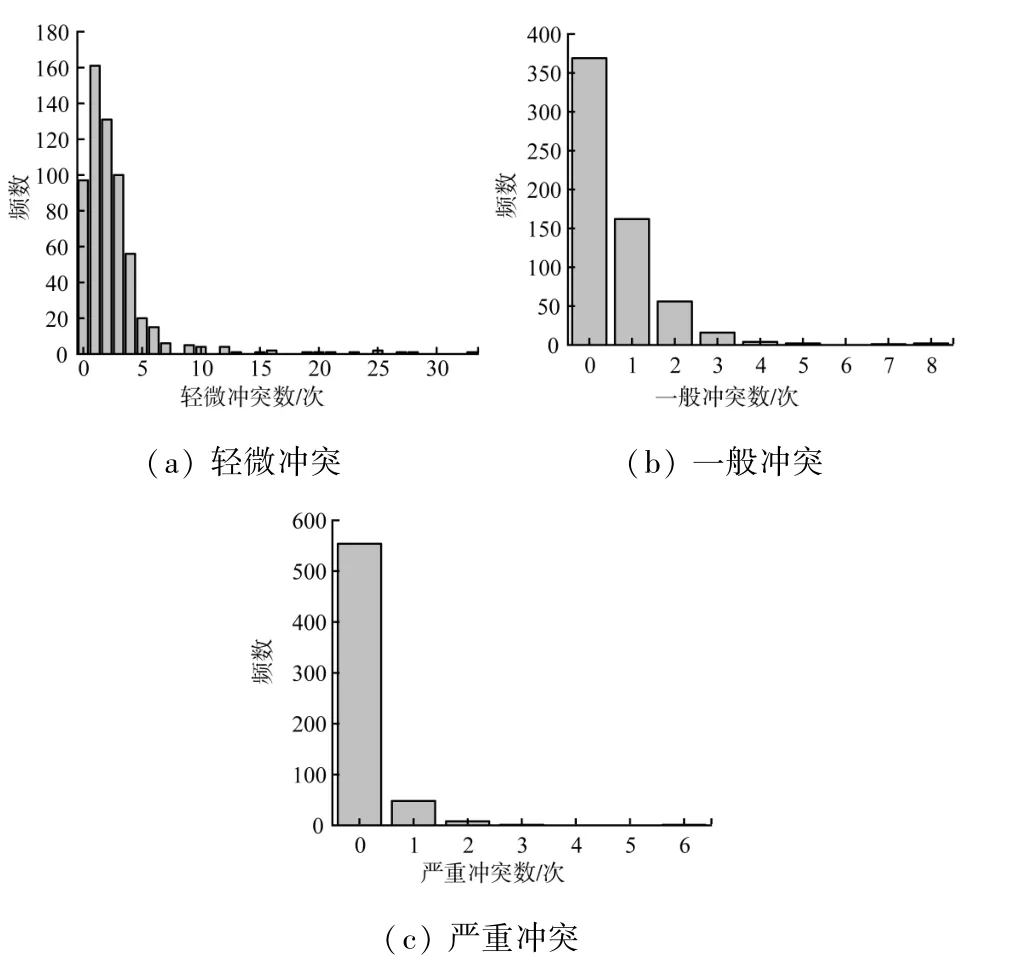
图3 3 种类型冲突次数的频数分布
分别计算3 种冲突程度的均值和方差,其中轻微冲突次数均值为2.603 次,方差为12.338,方差远大于均值,不满足Poisson 模型假设前提,单位时间内无冲突样本97 个,占总样本数15.85%,可以优先考虑NB 模型。一般冲突次数均值为0.606次,方差为0.976,均值与方差相差不大,单位时间内无冲突样本369 个,占总样本数60.29%,可优先考虑零膨胀结构模型。严重冲突次数均值0.119 次,方差0.190,单位时间内无冲突样本554 个,占总样本数90.52%,0 数据占比较大,可优先考虑采用零膨胀结构模型。
第二步,将提取到的交通流信息与3 种严重程度的交通冲突次数进行相关性分析,变量相关性矩阵如图4 所示。
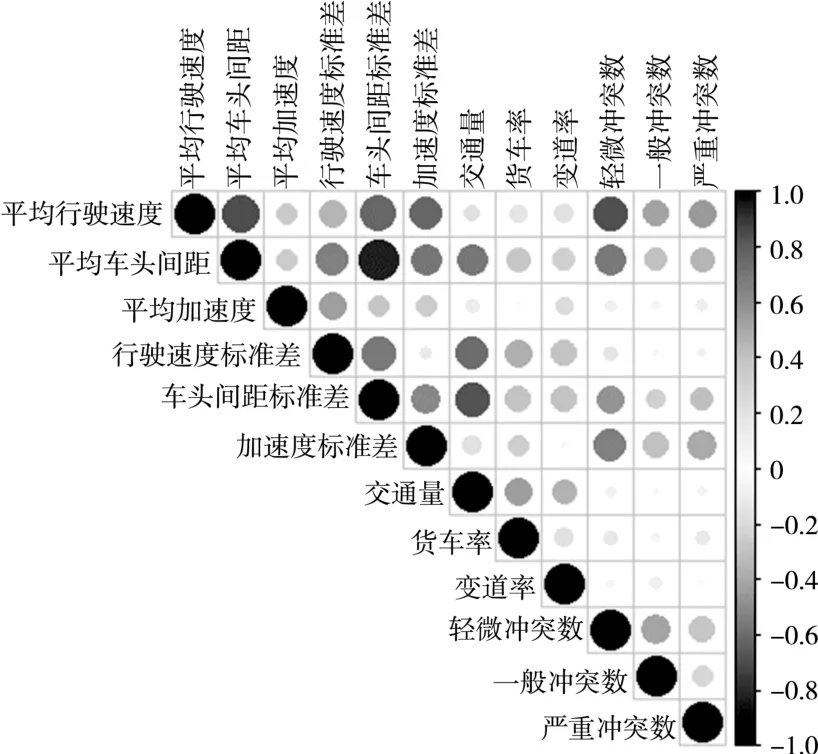
图4 变量相关性矩阵
根据影响因素与因变量之间的相关性系数大小,可以选择对因变量影响大的影响因素进行建模分析。同时,根据相关性系数可以选择相互影响较小的变量,从而避免多重共线性。
3.2 冲突次数预测模型
3.2.1 轻微冲突次数模型
对路段1 的轻微冲突次数分别采用不同计数模型进行回归分析,得到各模型的AIC 值、BIC 值、LL(log-likelihood,对数似然)值,轻微冲突次数各模型表现如表2 所示。其中NB 模型的AIC 值和BIC 值分别为2 143.07 和2 169.57,在4 种模型中相应AIC值和BIC 值最小,该模型的拟合效果最好。

表2 轻微冲突次数各模型表现
剔除不显著的影响因素,轻微冲突次数NB 模型参数如表3 所示,其中各影响因素的VIF 值均小于10,不存在共线性问题。此外,NB 模型的α估计值为0.095≠0,因此选用NB 模型进行回归分析是正确的。

表3 轻微冲突次数NB 模型参数
由回归结果可知,平均行驶速度和平均加速度与轻微冲突次数均呈负相关,随着平均行驶速度和平均加速度的增大,轻微冲突次数减少。在控制其他变量保持不变的情况下,平均行驶速度和平均加速度每增加1%,轻微冲突次数期望值分别减少0.91%和0.52%。两个方向的轻微冲突次数与加速度标准差、变道率呈正相关。加速度标准差和变道率每增加1%,轻微冲突次数期望值分别增加4.35%和3.45%。
3.2.2 一般冲突次数模型
一般冲突次数各模型表现如表4 所示,由表4 可知,ZIP 模型的AIC 值为1 178.21、BIC 值为1 209.13,在4 种模型中相应AIC 值和BIC 值最小,且LL 值较Poisson 模型和NB 模型较大,略小于ZINB 模型,ZIP 模型的综合表现最好。

表4 一般冲突次数各模型表现
采用ZIP 模型对一般冲突次数进行回归分析,一般冲突次数ZIP 模型参数如表5 所示,其中计数模型部分各影响因素的VIF 值均小于10,不存在共线性问题。

表5 一般冲突次数ZIP 模型参数
由计数模型参数可知,一般冲突次数与加速度标准差呈正相关,与平均行驶速度呈负相关。在控制其他因素不变的情况下,加速度标准差每增加1%,一般冲突次数期望值增加3.27%;平均行驶速度每增加1%,一般冲突次数期望值减少0.81%。对于零膨胀模型部分,平均行驶速度和平均加速度与一般冲突次数均呈显著正相关,变道率呈显著负相关。随着平均行驶速度和平均加速度的增大,出现一般冲突的可能性提高;随着变道率的增大,出现一般冲突的可能性降低。
3.2.3 严重冲突次数模型
严重冲突次数各模型表现如表6 所示,虽然严重冲突次数存在大量0 数据,但Poisson 模型的AIC 值(360.94)略大于NB 模型的AIC 值(360.88),Poisson模型的BIC 值(374.191)在4 种模型的BIC 值中最小,因此考虑采用Poisson 模型对严重冲突次数进行回归分析。

表6 严重冲突次数各模型表现
严重冲突次数Poisson 模型参数如表7 所示,其中VIF 值均小于10,不存在共线性问题。

表7 严重冲突次数Poisson 模型参数
值得注意的是,采用Poisson 模型时须考虑因变量是否存在过离散问题,在R 语言中采用“qcc”包对其进行检验得到P值为0(<0.05),因此存在过离散问题,可考虑采用Quasi-Poisson(类泊松)模型解决该问题。严重冲突次数Quasi-Poisson 模型参数如表8 所示。

表8 严重冲突次数Quasi-Poisson 模型参数
由表8 可知,严重冲突次数与加速度标准差呈正相关,与平均行驶速度呈负相关。在控制其他因素不变的情况下,加速度标准差每增加1%,单位时间内严重冲突次数的期望值增加36.93%;平均行驶速度每增加1%,单位时间内严重冲突次数的期望值减少0.92%。
4 结论
(1) 基于交通冲突技术,利用HighD 数据集以1 min 为单位时间提取了路段1 的交通特征指标以及冲突信息。根据TTC 的大小将轻微冲突、一般冲突以及严重冲突的阈值划分为(3 s,6 s]、(1.5 s,3 s]和(0 s,1.5 s]。分别考虑3 种不同严重程度冲突次数的Poisson 模型、NB 模型、ZINB 模型以及ZIP 模型,并根据AIC 值、BIC 值以及LL 值确定表现最好的模型。轻微冲突次数、一般冲次突数和严重冲突次数的预测中表现最佳的模型分别为NB 模型、ZIP 模型以及Poisson 模型。
(2) 对不同严重程度冲突次数的影响因素进行量化分析。3 种模型中加速度标准差和平均行驶速度都与冲突次数呈显著相关性。若保持其他影响因素不变,加速度标准差每增加1%,3 种严重程度的冲突次数期望值分别增加4.35%、3.27%和36.93%;平均行驶速度每增加1%,3 种严重程度的冲突次数期望值分别减少0.91%、0.81%和0.92%。
(3) 由于路段1 中处于拥堵状态的交通流较少,本研究中未分状态考虑交通流。对于处于不同交通流状态的车流,其冲突影响因素是否存在不同效应,值得进一步研究。
