空间引力波探测航天器高精度状态估计器设计

张东林，曹一凡，段战胜，王鹏程，郭 明，张永合

（1.西安交通大学 自动化科学与工程学院，西安 710049；2.中国科学院 微小卫星创新研究院，上海 201204）

引言

近年来，引力波探测已经成为当代物理学重要的前沿领域之一。其中空间引力波探测是指在太空中利用卫星编队或星座构建大型激光干涉仪，实现对中低频引力波信号的探测[1]。欧洲航天局（European Space Agency，ESA） 于1993年最早提出了空间引力波探测计划“激光干涉测量空间天线”（Laser Interferometer Space Antenna，LISA）项目，中国在2008年开始探讨空间引力波探测的可行性，先后开展了概念与方案设计、关键科学载荷研制等，并于2014年和2016年提出了“天琴计划”和“太极计划”[2-3]。

激光干涉测量对卫星无拖曳与姿态控制系统提出了极高的要求。引力波信号在空间中极其微弱，而探测环境存在着强噪声的干扰，因此探测系统必须保持足够的稳定才有可能捕获引力波信号[4-5]。此外，由于激光器功率有限且测量光束发散角很小，需要卫星进行精确的姿态控制实现高精度、高稳定度指向。卫星高精度姿态估计作为控制律设计和执行机构高精度执行的前提，显得尤为重要[6-7]。

卫星姿态确定方法通常可以分为确定性方法和状态估计法两类[8-9]。确定性方法无需姿态的先验知识和动态变化信息，直接利用各个时刻的矢量观测进行姿态确定[10]。TRIAD（TRIaxial Attitude Determination）姿态确定方法是第一个使用两个矢量观测确定航天器姿态的广泛普及方法[11]。除此之外还有QUEST （QUaternion ESTimator） 法[11]、SVD （Singular Value Decomposition） 法[12]、FOAM （Fast Optimal Attitude Matrix）法[12]以及Euler-q法[13]等。确定性方法具有明确的物理或几何意义，但该类方法要求参考矢量的参数足够精确。状态估计法是结合传感器测量方程和卫星状态方程，基于一定的估计准则，实时得到卫星状态变量的最优估计方法[14]。与确定性方法不同，状态估计法通常能提供被估计量的统计最优解。在一定程度上抑制了某些不确定性因素的影响，提高姿态确定的精度，因此在高精度姿态确定系统中多采用状态估计法。

卡尔曼滤波器已经在航天器姿态估计领域得到了广泛的应用[15]。为了更好地适应航天器动力学和量测模型的非线性，扩展卡尔曼滤波器得到了推广。随着四元数被用于姿态描述参数，Lefferts[16]提出了基于四元数的扩展卡尔曼姿态估计方法。然而使用四元数参数化的传统卡尔曼滤波器存在协方差矩阵奇异的问题。随着星载计算机性能的提高，一些先进的非线性滤波算法应用到了卫星姿态估计系统中。无迹卡尔曼滤波[17-18]，中心差分卡尔曼滤波算法[19]以及粒子滤波算法[20]相较于扩展卡尔曼方法具有更快的收敛速度和更高的精度。此外，由于基于容积卡尔曼滤波[21]的容积四元数估计器更适用于高维的非线性系统，因此它也被广泛应用于航天器系统状态估计中。

基于星敏感器和惯性传感器测量的空间引力波探测航天器系统状态估计本质上是一个非线性约束估计融合问题。上述已有的常规非线性滤波算法无法直接应用于该航天器系统状态估计问题。在本文中，提出了一种线性化四元数量测的卡尔曼滤波算法，以实现空间引力波探测任务中航天器状态的高精度实时估计。该方法结合平台的超稳超静特性，通过对四元数姿态测量在航天器小角度变化下的近似变形来满足卡尔曼滤波器的线性假设条件，并结合航天器系统离散时间状态空间模型和多源异构数据实现航天器系统状态的高精度估计。在空间引力波探测任务中的捕获建链阶段，指向估计精度应达到0.1 μrad量级。航天器系统具有高精度的测量传感器，状态估计任务则需要满足航天器姿态量测误差压缩率高于40%。设计的状态估计器将系统传感器噪声进一步压低了至少一个数量级，满足空间引力波探测航天器系统状态高精度实时估计的需要，是引力波探测重大科学实验计划顺利实施的前提。

1 状态空间建模

1.1 状态方程建模

应用牛顿–欧拉公式，可得到空间引力波探测中航天器系统动力学模型，其线性化后相应的二阶微分方程为

由于M阵可逆，将等式两侧同乘M-1，得到

由上述状态空间建模得到系统连续时间的状态空间描述，已知这是一个近似线性时不变的系统，假设系统采样周期为T，由线性系统理论可知，连续时间的LTI （Linear Time Invariant）系统的非齐次方程的解为

对于式（4），考虑从t0=kT到t=(k+1)T之间的时间段，并由于这一时间段内u(t)=u(kT)，d(t)=d(kT)以及w(t)=w(kT)，可以得到

对于积分项，令t=(k+1)T-τ，则dτ=-dt。由于在一个采样周期内系统可看作LTI系统，因此可以将积分项内的B′、F′、G′项移到积分项外。通过化简整理可得到

将式（6）简记为

备注：由于航天器系统动力学模型中质量矩阵M是非对角矩阵，因此航天器本体姿态和两个检验质量块的位姿存在耦合关系。如果不考虑两个检验质量块的位姿信息，就无法实现航天器姿态的高精度估计。此外，在空间引力波探测任务中，星间激光链路的建立和保持需要协调控制卫星及两个检验质量块来共同完成。因此，在航天器姿态估计中，需要同时估计两个检验质量块的位姿信息。

1.2 量测方程建模

首先利用姿态四元数定义卫星本体相对地面惯性参考坐标系的姿态为qib∈R4，记为qib=[qib,0,qib,1,qib,2,qib,3]T，有如下形式

其中：e=[e1,e2,e3]T表示欧拉轴的三维方向向量且满足||e||2=1，θ表示欧拉角参数。姿态四元数的4个参数非独立，满足以下条件

2 量测线性化

从式（8）中可以看出系统关于卫星本体姿态四元数的量测是非线性的，由于系统动力学方程复杂且估计状态维数高、初始化难度大，直接应用非线性滤波方法进行状态估计会出现收敛缓慢、容易发散等问题。现将卫星本体姿态四元数的量测部分进行线性化处理。

根据欧拉定理，刚体绕固定点的位移也可以是绕该点的若干次有限位移的合成，在用姿态四元数表示姿态参数的方法中，连续两次转动后的姿态四元数等于各次转动的四元数的乘积。基于星敏感器读出，可以得到偏差四元数测量

展开形式为

其中：qr为设定参考姿态：q为卫星的真实姿态；qn为噪声。

将量测方程中姿态四元数的部分进行线性化处理，卫星本体的角度参数与姿态四元数量测之间的相互转换关系如下

将式（12）进一步展开

由于四元数的参数非独立且满足条件||q||2=1，在欧拉角为小角度（Δq0≈1）的情况下，有以下近似关系

将式（12）代入式（13）重写为

展开可得

由此得到系统关于姿态四元数的非线性量测部分的线性化结果。

3 滤波算法

其中：H∈R15×36是线性化后的测量矩阵；v(t)∈R15是量测系统的读出噪声。在相邻的两个采样时刻之间，读出噪声v(t)通过零阶保持器保持不变。此时量测方程是状态向量和读出噪声的加性组合，即得到离散时间量测方程为

通过系统离散化和量测线性化处理，将基于星敏传感器非线性量测的卫星动力学系统和量测系统转换为满足卡尔曼滤波线性高斯假设的离散状态空间模型，即

基于卡尔曼滤波原理，可以得到线性化四元数量测的高性能状态估计算法。预测

更新

此外，进一步分析了设计的滤波器的计算复杂度。定义n为系统状态x(k)的维数，nd为执行器扰动d(k)的维数，nw为系统噪声w(k)的维数，以及m为传感器量测z(k)的维数。然后可以得到线性化四元数卡尔曼滤波算法的计算复杂度

相较于标准的卡尔曼滤波器（尽管其不能应用到该任务中），本文中设计的卡尔曼滤波器并没有额外增加计算复杂度。因此，在有限星载计算条件下，设计的基于线性化四元数量测的卡尔曼滤波算法可以用于空间引力波探测航天器系统状态的高精度估计。

4 仿真验证

设置仿真采样时间为T=0.1 s，仿真时长为N=50 000 s。初始的卫星状态设置为x(0)=[0′;0;3e-5;0;e-5;0;0;0;3e-5;0′],P0=e-25×I。建立MATLAB/Simulink仿真模型，对天基引力波系统进行状态估计与结果分析。在实验结果中，我们将滤波估计结果分别与真实值和测量值进行比较。为了便于比较分析，定义性能指标：平均量测误差、平均估计误差、误差减小率（Error Reduction Rate，ERR）。

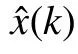
使用最大短时抖动指标衡量状态估计与量测的控制效果。最大短时抖动性能的计算式如下

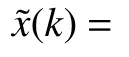
比对滤波前后控制误差的频谱分析滤波的性能。这里控制误差是指估计值/量测值减去引导率信号的误差，即可表示为

从图1所示的状态仿真结果可以看出状态估计方案抑制了多源复杂噪声的影响，实现了非线性量测下卫星位姿的实时估计。与系统传感器的量测值相比，估计值更为平滑且精确地跟踪到卫星的真实状态。从图2所示的结果可以更直观地看出估计误差明显小于量测误差的波动范围，在数值上更接近0。从表1可以看出单个测试质量的位姿以及卫星的三维姿态的估计结果误差都小于量测结果误差，姿态的估计误差成功降低了一个数量级，且非线性量测的卫星姿态估计结果的误差减小率ERR均达到了45%及以上，因此基于非线性量测线性化设计的卡尔曼滤波器可以得到更高精度的卫星状态，估计结果代替测量结果为整个系统中控制器模块提供更高精度的卫星实时状态信息。通过计算卫星姿态估计值与量测值的最大短时抖动来衡量系统控制误差的RMSE性能。从图3可以看出，在时间窗长度内卫星姿态角度估计值的最大短时扰动指标均小于量测值的最大短时扰动指标。同时通过控制误差频谱图反映状态估计对系统控制误差的影响。从图4可以看出，使用状态估计值的控制误差频谱相较于量测值在高频处幅值显著衰减，在高频处其控制误差的方差更小。因此使用基于非线性量测线性化设计的卡尔曼滤波器使得系统有更好的控制性能。

表1 状态估计性能比较Table 1 Performance comparison of state estimation

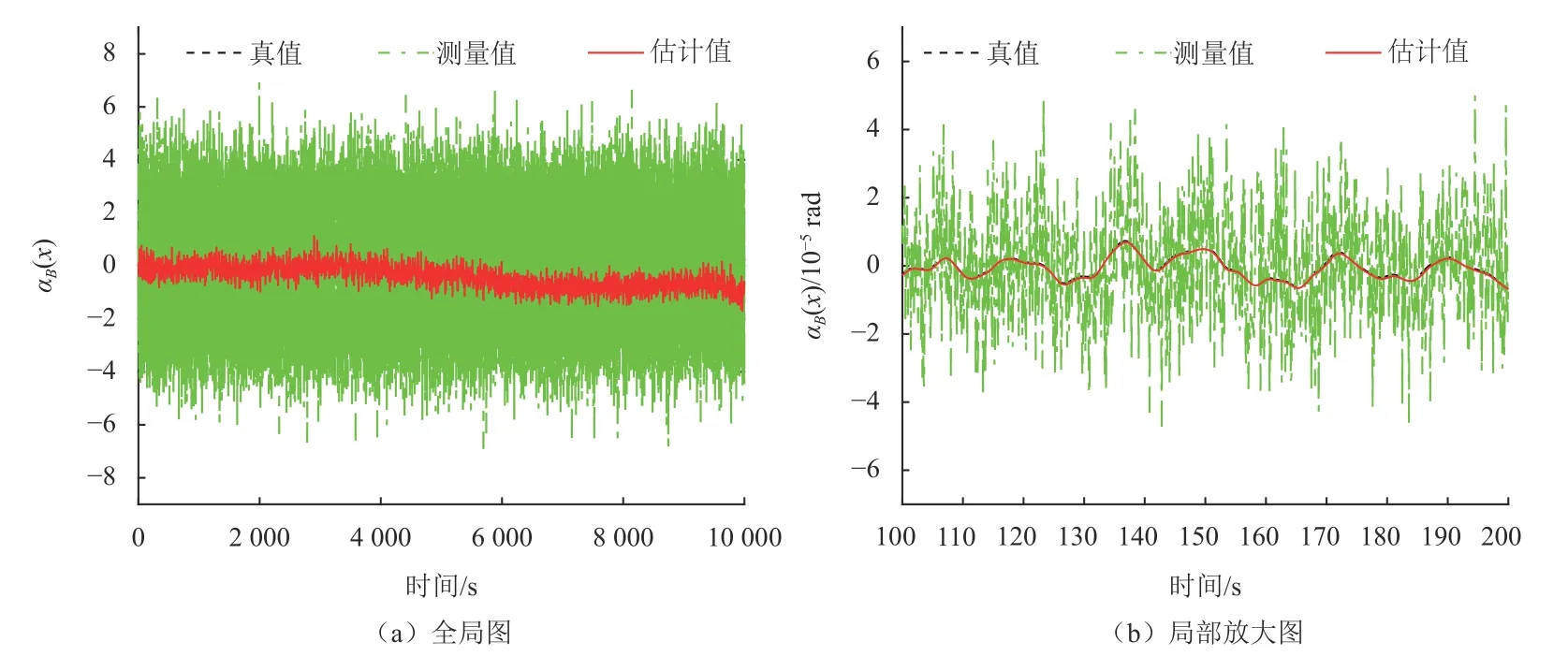
图1 αB(x)状态仿真结果图Fig.1 αB(x)State simulation results

图2 αB(x)估计误差对比图Fig.2 αB(x)Estimation error comparison

图3 αB(x)最大短时抖动Fig.3 αB(x)Maximum short-time jitter

图4 αB(x)滤波前后控制误差频谱Fig.4 αB(x)Control error spectrum

5 结论

本文针对空间引力波探测卫星对准阶段状态实时估计任务，基于星敏感器和惯性传感器等多源异构信息设计了一种线性化四元数量测的高性能状态估计器。首先对系统动力学模型进行离散时间状态空间建模；其次利用参考四元数信息对星敏感器非线性量测模型线性化处理，提出了基于卡尔曼滤波器的高性能状态估计算法，从而实现空间引力波探测航天器系统状态的在轨高精度估计；最后建立MATLAB/Simulink闭环仿真系统。仿真结果表明，在保证较低计算复杂度的前提下，所设计的估计方法能够达到很好的估计效果，满足引力波探测任务中航天器状态高精度实时估计的需要，进一步验证了提出的状态估计器的可行性。