一种离散轨道数据约束下的地月三体轨道脉冲转移算法

王义宇，罗宇航，徐田来，包为民，袁 帅，张泽旭，李宸硕，胡志杰

（1.哈尔滨工业大学 航天学院，哈尔滨 150001；2.中国航天科技集团有限公司，北京 100048）

引言

近年来，不同太空机构使用多种类型的航天器重新访问了月球，各航天强国均提出更富挑战性的探月计划[1-4]。不管是针对月球的长期探测和建设月球空间站等在轨任务，还是针对载人登月和建造月球基地等着陆任务，借助地月空间内的多种特殊轨道从而以更低的成本完成任务成为关键问题，而其中设计各个特殊轨道之间的转移轨道更是所有任务的重要基础[5-6]。

目前，地月空间内的局部周期轨道得到了广泛关注。考虑到轨道能量与稳定性，研究对象主要以绕月的大幅值逆行轨道（Distant Retrograde Orbit，DRO）和绕平动点的Lissajous轨道、Halo轨道族以及其中较为特殊的近直线晕轨道（Near-Rectilinear Halo Orbit，NRHO）为主[7-8]。

各学者根据不同轨道的不同特性设计了多种脉冲转移轨道的建模和计算方法：孙俞等[9]针对平动点轨道间两脉冲转移问题设计了三体Lambert求解算法、潘迅等[10]基于主矢量理论提出一种快速计算双脉冲转移轨道的方法、Tan等[11]利用周期轨道研究了低能量双脉冲转移问题、 Zimovan-Spreen等[12]对NRHO和DRO进行了动力学分析并根据流形设计了转移轨道、曾豪等[13]采用配点法与局部优化算法构造出满足近月点约束的环月轨道与平动点轨道之间燃料最优往返转移、Oshima[14]以平面李雅普诺夫轨道的垂直稳定流形为基础设计了NRHO与DRO之间的转移轨道，也有学者提出采用深度强化学习如PPO、MCTS等普适方法设计地月空间转移轨道[15-16]。

从研究对象看，已有研究主要集中于地月停泊轨道与特殊轨道之间的转移，而对于特殊轨道之间的转移问题研究较少；从优化问题模型看，对于两脉冲转移，大多建模为三体模型下的两点边值问题[17-19]，多脉冲转移常考虑脉冲点位置等特殊约束并建模为非线性优化问题[11,20]；从求解算法看，一般采用数值迭代方法或成熟的非线性求解器进行求解[20]，但解的收敛性和最优性对初值依赖度较高，求解难度较大，一般会采用智能算法（如粒子群算法、遗传算法、差分进化算法等[21-22]）或根据起始和目标轨道特性[13,20]进行初值的简单搜索，普适性较低。

基于以上问题，本文以地月空间中特殊轨道之间转移为研究对象，引入离散轨道数据作为转移轨道的起点和终点约束，提高对不同轨道的适应能力，并将最小脉冲转移问题进行拆分重构，转化为双层优化问题，降低问题求解难度，同时兼顾全局最优性和计算效率，在双层优化模型的基础上提出了双层优化求解算法，避免了初值敏感问题，实现了多种类型轨道间的最小脉冲转移轨道设计。

1 圆形限制性三体问题模型

1.1 动力学模型

圆型限制性三体问题（Circular Restricted ThreeBody Problem，CRTBP）是对实际三体问题的一种理想近似，是研究三体轨道动力学行为的基础。在CRTBP下，可定义会合坐标系B-xyz，其坐标原点在三体系统的质心B上，x轴由系统质心B指向第二主天体的质心，xy坐标面即两个主天体相对运动平面，x轴与y、z轴构成右手坐标系，如图1所示。

图1 圆型限制性三体动力学模型Fig.1 Circular restricted three-body dynamic model

在三体会合坐标系中，航天器的动力学模型可描述为[9]

其中：x，y，z表示航天器在三体会合坐标系中的位置；μ表示两主天体的质量比参数；r1、r2分别表示航天器到两主天体的距离。

另外在CRTBP模型下，存在雅可比常数可表征三体系下航天器所在轨道的能量

1.2 CRTBP下特殊轨道

圆型限制性三体问题动力学模型具有5个平衡点，也称为平动点。围绕平动点与主天体也存在着很多特殊的周期解，构成了三体模型中特殊的周期轨道和拟周期轨道。主要包含绕平动点的周期轨道如Halo、Lissajous轨道和绕天体的周期轨道如大幅值逆行轨道等，根据不同要求，往往可得到同类型的一族轨道。图2中绘出了典型的局部周期轨道族（Halo、Lissajous、DRO），一般对会合坐标系下速度、距离等进行归一化处理，以下仿真图中距离的单位取为归一化单位，即1LEM=384 400 km。

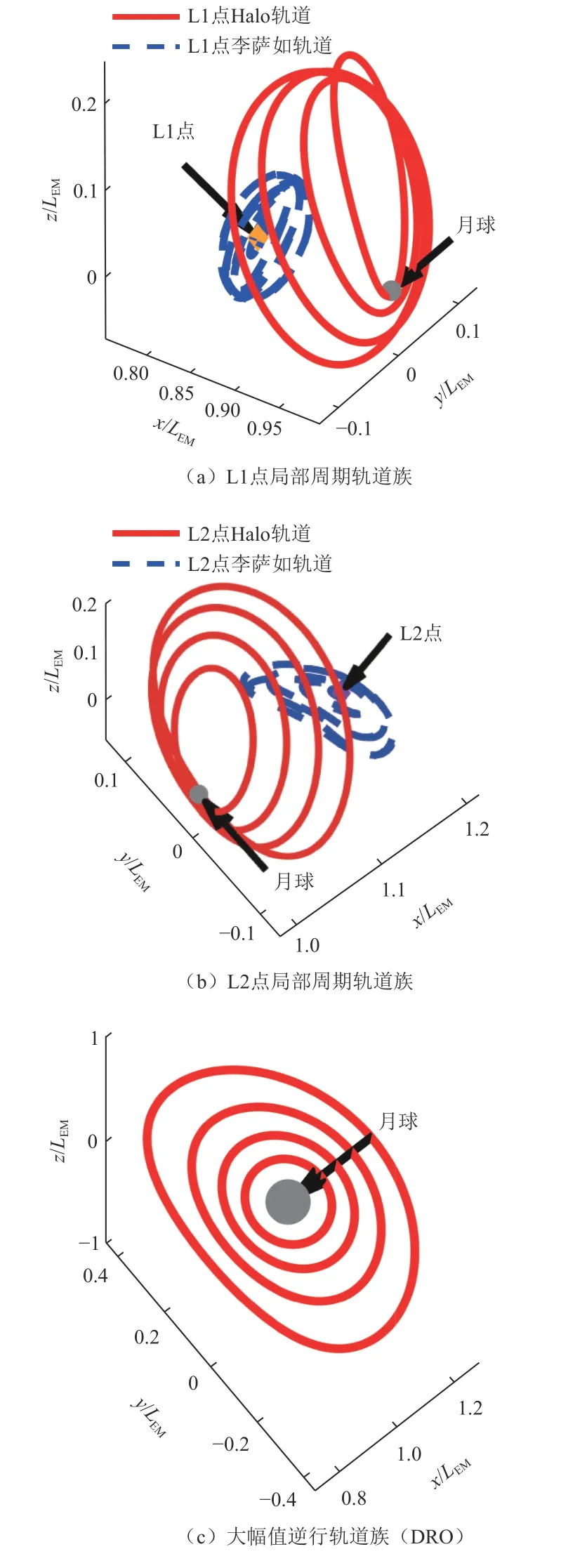
图2 地月三体系统下的局部周期轨道示意图Fig.2 Local periodic orbit under Earth-Moon CRTBP

Halo轨道族及其特殊的一类近直线晕轨道在未来具有较为突出的应用价值，对月球探测以及月球南北极着陆具有重要意义。而大幅值逆行周期轨道DRO具有较高的稳定性，因此适宜于月球空间站或探测器的长期在轨任务需求[19]。

此外不变流形也是基于CRTBP模型的主要理论之一。在CRTBP模型下，存在稳定流形流入平动点轨道，还存在受扰动后流出平动点轨道的不稳定流形。对于与其它特殊轨道相接的不变流形可设计低能转移轨道，对于不与目标轨道相接的流形，也可通过较小的速度脉冲实现轨道转移[23-24]。Halo轨道的稳定流形与不稳定流形示意图如图3所示。

图3 Halo轨道的稳定流形与不稳定流形Fig.3 Stable and unstable manifolds of Halo orbits

然而即使CRTBP是三体问题的简化模型，其动力学模型仍较为复杂。对于前文提及的特殊周期轨道以及不变流形，难以给出精确的解析解。目前主流的求解方式仍是在近似解析解的基础上通过微分修正或多点打靶等方法进行积分修正，进而得到较为精确的数值解，并一般以一定时间步长离散的轨道数据形式给出。

2 最小脉冲转移问题建模

地月系统下特殊轨道的最小脉冲转移问题可定义为：在多次脉冲消耗总燃料或总能量最小的情况下，实现起始轨道到目标轨道的转移。本文讨论最一般的情况：转移轨道起点与终点不固定、转移时间不固定、起始轨道与目标轨道类型不固定。考虑理想假设：在脉冲时刻，航天器在地月三体系统空间中的位置连续、速度产生突变。

为了尽可能地保证轨道的精确，本文在进行转移轨道的设计时，将起始轨道与目标轨道以离散数据构成的数据表的形式给出，从而约束转移轨道起点与终点的位置与速度。这种方法不仅保证了起点与终点的精度，同时也极大拓展了算法的普适性。起始与目标轨道不仅可以是特定类型的某一条轨道、某一类型的轨道族，同时也适用于借助不变流形的转移轨道设计，即不稳定流形作为起始轨道或稳定流形作为目标轨道。

考虑最一般的n+1次脉冲情况，脉冲时刻分别为t=[t0,t1,t2,···,tn]1×(n+1)，分别对应着速度改变量为Δv=[Δv0,Δv1,Δv2,···,Δvn]3×(n+1)。可定义指标为燃料最优或能量最优[25]

约束条件主要包括动力学约束、始末状态约束、脉冲约束、脉冲点约束以及转移时间约束等。

1）动力学约束

对圆型限制性三体问题下的动力学方程式（1）进行变换，可写为

定义各个脉冲时刻对应的航天器状态为

X0,X1,X2,···,Xn

在没有脉冲作用时，航天器应始终满足动力学方程，可表示为积分形式

2）始末状态约束

始末状态约束要求转移轨道的起点位于起始轨道上、终点位于目标轨道上。由前文提出本文起始轨道与目标轨道基于离散轨道数据构成的数据表给出，可分别定义起点可行数集与终点可行数集

其中：p、q为轨道数据的离散点数目；Xcj与Xtl分别对应离散的轨道数据，且每点应包含时刻、位置与速度，共7维，即

转移轨道起点和轨道终点为X0和Xn，即第一次脉冲时刻以及最后一次脉冲时刻对应的航天器状态。始末状态约束即要求航天器在起始时刻未施加脉冲时的状态是起始轨道数据中的一点，且在终端时刻施加脉冲后的状态是目标轨道数据中的一点，则约束可表述为

3）其它约束

对于各个脉冲时刻要求位置连续，脉冲前后可表示为

此外还可能对脉冲点存在其它限制，如要求脉冲点的位置等。可统一写为如下形式

考虑脉冲上限，可表示为如下约束

考虑转移时间上限，同时时间序列应为递增顺序，可表示为如下约束

综上，可建立最小脉冲转移问题如问题1所示。

问题1：

3 脉冲转移问题重构与算法设计

3.1 双层优化问题建模

将所有优化变量拆分为两部分：起点与终点的状态、脉冲时间序列为上层变量，脉冲序列为下层变量。相应的，问题1的约束条件也可拆分为两部分，从而重构为双层优化问题如问题2所示。

问题2：

双层优化实质上是将最小脉冲转移问题拆分为两步进行：第一步在起始轨道和目标轨道上选点，并给出这两点之间的脉冲时间序列；第二步建立最优控制问题模型，在确定起点和终点以及转移时间的情况下仅优化控制量即优化脉冲序列，优化指标为燃料最优或能量最优。上层问题求解方法选用具有自治能力的粒子群算法（Adaptive Genetic Particle Swarm Optimization，AGPSO）的智能算法，下层问题求解方法选用序列二次规划算法（Sequential Quadratic Programming，SQP）。

3.2 上层优化问题求解算法设计

由于行数/列数与此行/列的数据存在固定的映射关系，不同行/列的映射关系并不相同，每个行数/列数与其对应的数据均可描述为某个特定的未知函数

对于解析的迭代方法来说，不能显式表达的函数往往不利于求解。但得益于智能算法的普适性，可通过寻找行数或者列数实现降维：原本要优化的起点和终点状态共12维的变量，通过表格数据的自然约束降维为2维，即起始轨道数据表中的某行或某列以及目标轨道数据表中的某行或某列（对于一族轨道数据，可通过三维表格进行约束，此时优化变量降维为4维），可建立行数/列数的约束如下

因此可重新构建上层优化问题如下。

问题3：

由于上层优化问题优化变量与优化指标关系不明确，且优化变量的初值难以设计，因此选择智能算法进行求解。综合考虑计算效率与收敛性，选择AGPSO进行优化。在传统的PSO算法中，所有粒子在局部搜索和全局搜索的效果方面都是相同的，因此可以认为所有粒子是一个具有同一种策略的群。各个粒子的位置和速度更新可表示为

然而在任何基于种群的优化算法中，使用具有共同目标的不同自治群体，理论上可以使算法具备更多的随机或定向的搜索。AGPSO的核心思路为利用不同的策略来更新c1和c2，对自治群进行数学建模[26]。换言之，这些群体在关注个体和全局表现的程度上表现得不同。本文设计4个群体，即设计4种c1和c2的变化策略，更新函数如表1所示。

总之，这种传统教学与PBL教学相结合的教学方式，理论成绩与实践考核等方面均有提高，学生满意度高，既提升了师资队伍水平，又培养出敏而好学的学生，加强了学生人文素养的培养，激发了学习的热情。教学模式有机的结合能够发挥两方面的优势，更好地促进健康管理的理论与教学实践。

表1 4种 c1和 c2的更新策略Table 1 Four updating formula for c1 and c2

后文仿真中，上层优化问题均基于AGPSO算法进行求解，其它参数如表2所示。

表2 AGPSO算法相关参数表Table 2 Parameters of AGPSO algorithm

3.3 下层优化问题求解算法设计

经过拆分处理后，下层优化问题的自由变量仅剩3(n+1)维的脉冲序列 Δv。根据上层优化所得到的起点与终点状态以及各个脉冲时刻，可建立最优控制问题如下。

问题4：

问题4仍为含约束的非线性优化问题，但相比于问题1，变量个数大大减少、求解难度大大降低。当转移过程仅为两脉冲时，问题可直接建模为三体模型下的Lambert问题，可采用如牛顿–同伦法[27]、拟线性化–局部变分迭代法[28]等算法求解。但涉及多脉冲或包含其它约束限制时，固定转移时间的两点边值约束问题求解方法不再适用。针对此类非线性问题，采用SQP算法。求解过程本文不再赘述，相关参数选取如表3所示。

表3 SQP算法相关参数表Table 3 Parameters of SQP algorithm

虽然SQP算法本身较为成熟，但其仍存在局部收敛、初值敏感等问题[6]。对于本文所构建的非线性规划问题4来说，由于其优化指标为优化变量的2–范数之和或2–范数平方和的形式，所期望脉冲尽可能小，即问题4的解尽可能靠近 0。考虑到SQP算法的局部收敛性，选取初值为Δv=0，认为问题4的期望解在其邻域内①下层优化问题4的求解受上层优化问题3的结果影响。当SQP算法初值选为0时，上层结果可能导致下层优化不收敛，表明此时求解的脉冲较大，不在0的邻域内。同时也表明了当次求解上层结果的不合理，因此可对此结果赋予大指标作为惩罚，进入下一次迭代求解。。在一定程度上避免了SQP对初值敏感、难以设计迭代初值的问题。

通过结合AGPSO与SQP对问题3与问题4双层优化模型进行迭代求解，可得到设置最大迭代次数内的最小脉冲，整体求解框架如图4所示。

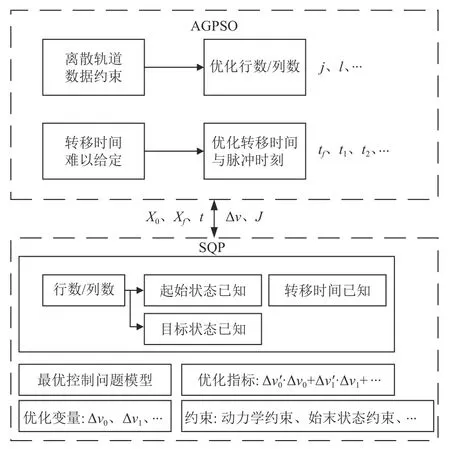
图4 基于AGPSO和SQP的双层优化求解框架Fig.4 Two-layer optimization solution framework based on AGPSO and SQP

4 仿真分析

4.1 指定轨道间的转移轨道

对于指定轨道间的脉冲转移问题，本文选取3种轨道转移场景进行仿真：①绕L1点NRHO轨道到绕L2点Halo轨道的转移；②绕L1点Lissajous轨道到DRO轨道的转移；③绕L1点NRHO轨道到DRO轨道的转移。

1）绕L1点NRHO到绕L2点Halo的转移

选择振幅为125 000 km的L1点NRHO和振幅为100 000 km的L2点Halo作为起始轨道和目标轨道，离散点均为2 000个。采用两脉冲与三脉冲两种方式进行轨道转移，指标选择为能量最优。通过算法可求得转移轨道分别如图5（a）、（b）所示，指标随迭代的变化曲线如图5（c）所示。

图5 L1点NRHO–L2点Halo的两脉冲与三脉冲转移Fig.5 Transfer from L1 NRHO to L2 Halo using two impulses/three impulses

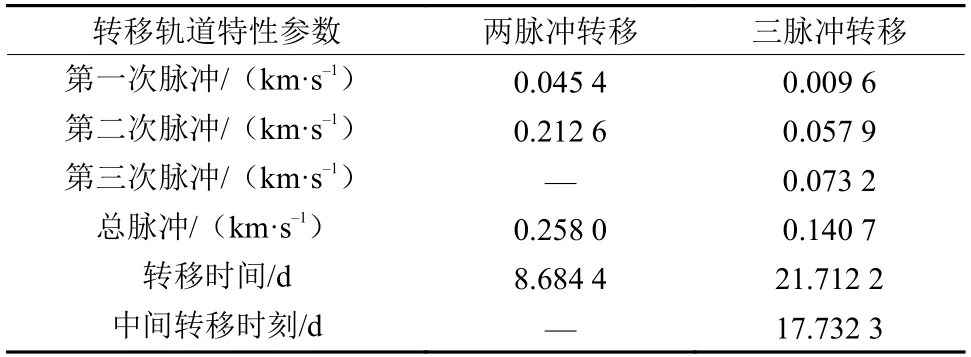
表4 L1点NRHO–L2点Halo的脉冲转移优化结果Table 4 Transfer Impulse from L1 NRHO to L2 Halo

2）绕L1点Lissajous轨道到DRO轨道的转移

选择振幅为125 000 km的L1点Lissajous轨道和振幅为496 600 km的DRO作为起始轨道和目标轨道，离散点均为2 000个。同样采用两脉冲与三脉冲两种方式进行轨道转移，指标选择为能量最优。通过算法可求得转移轨道分别如图6（a）、（b）所示，指标随迭代的变化曲线如图6（c）所示。

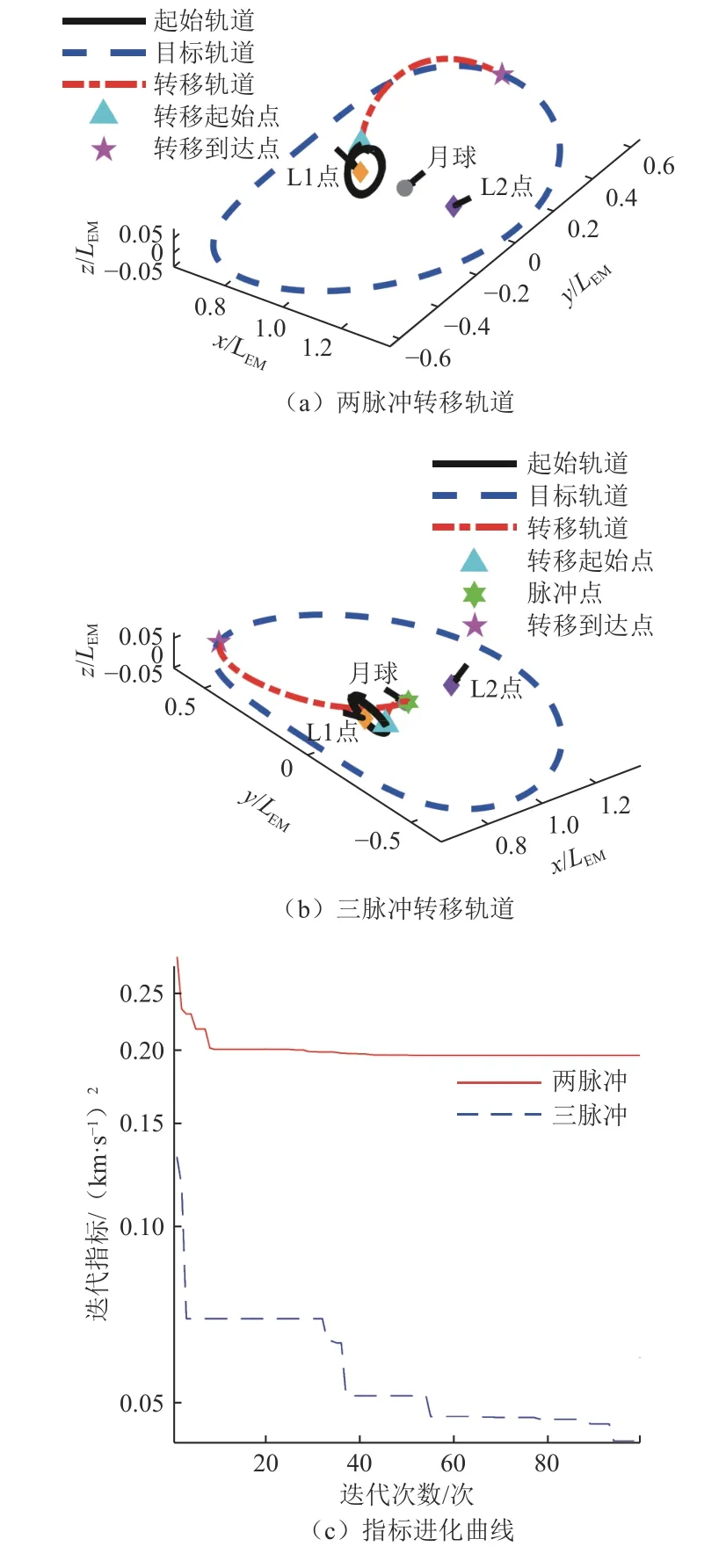
图6 L1点Lissajous轨道–DRO的两脉冲与三脉冲转移Fig.6 Transfer from L1 Lissajous to DRO using two impulses/three impulses

由图6（a）、（b）所示，转移轨道通过两脉冲和三脉冲完成L1点Lissajous轨道至DRO的转移，同时实现起始点、目标点、中间脉冲点以及转移时间的选取。根据图6（c）可得，随着算法迭代计算，能量指标逐渐收敛至较低的值，从而实现设定代数内的最优能量转移，可得到计算结果如表5所示。

表5 L1点Lissajous轨道–DRO的脉冲转移优化结果Table 5 Transfer Impulse from L1 Lissajous orbit to DRO

3）绕L1点NRHO轨道到DRO轨道的转移

选择振幅为125 000 km的L1点NRHO轨道和振幅为285 600 km的DRO作为起始轨道和目标轨道，离散点均为2 000个。采用两脉冲、三脉冲以及月球借力3种方式进行轨道转移，指标选择为能量最优。

其中，月球借力转移策略为：在三脉冲转移的基础上再限制中间脉冲点位置作为问题4的约束条件。要求中间脉冲点为近月点，即脉冲点相对月球中心的位置矢量与速度矢量垂直，同时要求中间脉冲点距月球表面高度小于500 km，可表示为

通过算法可求得转移轨道分别如图7（a）、（b）、（c）所示，指标随迭代的变化曲线如图7（d）所示。

图7 L1点NRHO–DRO的两脉冲、三脉冲与月球借力转移Fig.7 Transfer from L1 NRHO to DRO using two impulses/three impulses/gravity assist

由图7（a）、（b）、（c）所示，转移轨道通过两脉冲、三脉冲以及借月飞行3种方式完成L1点NRHO轨道至DRO的转移，同时实现起始点、目标点、中间脉冲点以及转移时间的选取。根据图7（d）可得，随着算法迭代计算，3种不同转移方式的能量指标均能逐渐收敛，可得到计算结果如表6所示。

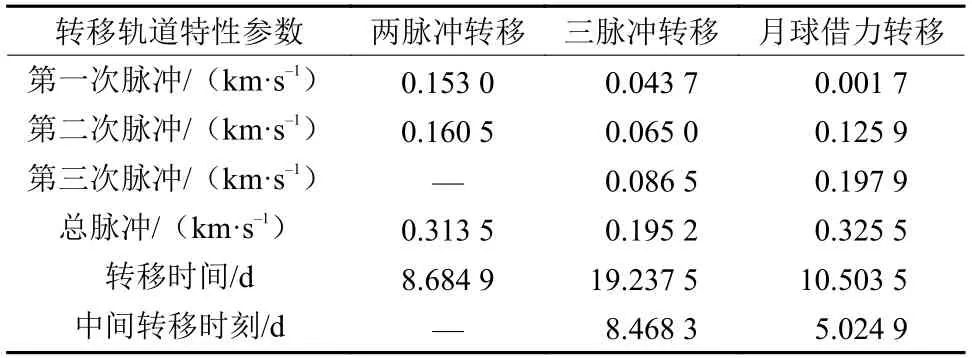
表6 L1点NRHO轨道–DRO的脉冲转移优化结果Table 6 Transfer Impulse from L1 NRHO to DRO

另外由图7（c）可见，月球借力飞行的中间脉冲点也满足所设要求，能够实现借助月球引力进行转移。但添加近月脉冲的限制条件后，算法在50个粒子、100次迭代的情况下，月球借力飞行的结果并不如两脉冲与三脉冲转移。然而根据图7（a）、（b）两图可直观看出，两脉冲与三脉冲转移的轨道实际上也借助了月球引力从而改变了速度方向，而三脉冲不限制中间点脉冲，可能存在更优的转移轨道，可见本文提出的算法具有较强的搜索能力。

4.2 轨道族间的转移轨道

对于轨道族间的脉冲转移问题，本文选取两种轨道转移场景进行仿真：①绕L1点Halo轨道族到绕L2点Halo轨道族的转移；②绕L1点Halo轨道族到DRO轨道族的转移。

1）L1点Halo轨道族到L2点Halo轨道族的转移

选择振幅范围为67 850～96 600 km的绕L1点Halo轨道族和振幅范围为64 350～99 250 km的绕L2点Halo轨道族作为备选的起始轨道和目标轨道，离散的轨道数据构成三维矩阵，维度分别为：6 × 2000 × 80和6 × 2 000 × 80。采用两脉冲、三脉冲两种方式进行轨道转移，指标选择为能量最优。通过算法可求得转移轨道分别如图8（a）、（b）所示，指标随迭代的变化曲线如图8（c）所示。

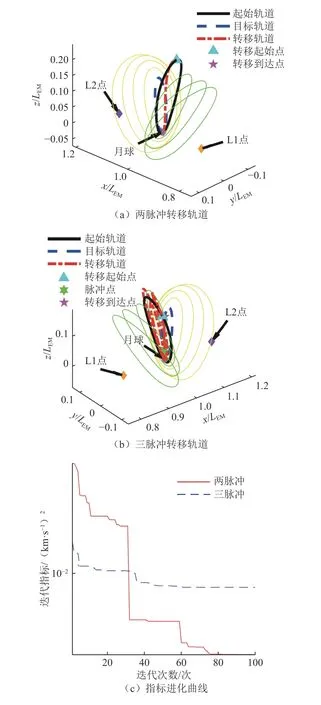
图8 L1点Halo轨道族–L2点Halo轨道族的两脉冲与三脉冲转移Fig.8 Transfer from L1 Halo family to L2 Halo family using two impulses/three impulses

由图8（a）、（b）所示，算法选择了两个轨道族中距离最接近的两条轨道，即能量相差最少的轨道为最优转移方案。通过两脉冲和三脉冲完成L1点Halo轨道至L2点Halo轨道的转移，同时实现起始点、目标点、中间脉冲点以及转移时间的选取。根据图8（c）可得，随着算法迭代计算，能量指标逐渐收敛至较低的值，从而实现设定代数内的最优能量转移，可得到计算结果如表7所示。

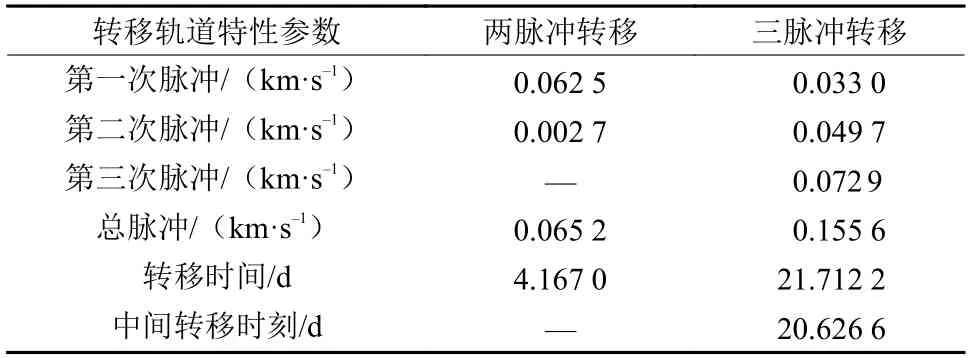
表7 L1点Halo轨道族–L2点Halo轨道族的脉冲转移结果Table 7 Transfer Impulse from L1 Halo family to L2 Halo family

2）L1点Halo轨道族到DRO轨道族的转移

选择振幅范围为67 850～96 600 km绕L1点Halo轨道族和振幅范围为86 450～285 600 km的DRO轨道族作为备选的起始轨道和目标轨道，离散的轨道数据构成三维矩阵，维度分别为：6 × 2 000 × 80和6 × 2 000 × 80。采用两脉冲、三脉冲两种方式进行轨道转移，指标选择为能量最优。通过算法可求得转移轨道分别如图9（a）、（b）所示，指标随迭代的变化曲线如图9（c）所示。

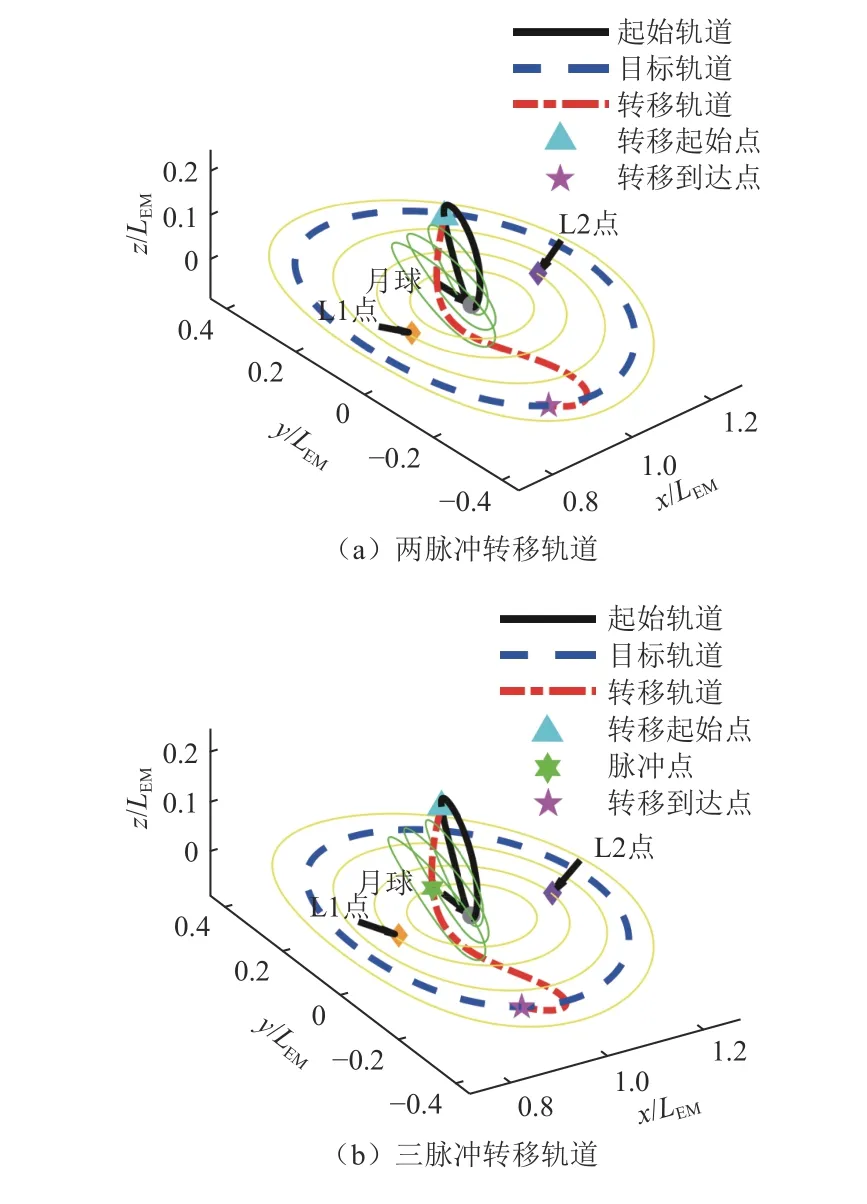
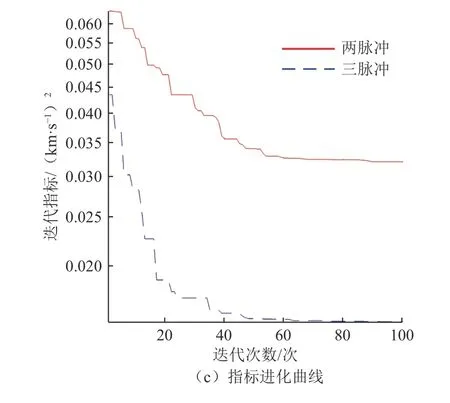
图9 L1 Halo轨道族–DRO轨道族两脉冲与三脉冲转移Fig.9 Transfer from L1Halo family to DRO family using two impulses/three impulses

由图9（a）、（b）所示，算法通过两脉冲和三脉冲完成L1点Halo轨道至DRO轨道的转移，同时实现起始点、目标点、中间脉冲点以及转移时间的选取。使用两脉冲和三脉冲的差别很小，转移轨道重合度较高。根据图9（c）可得，随着算法迭代计算，能量指标逐渐收敛，可得到计算结果如表8所示。

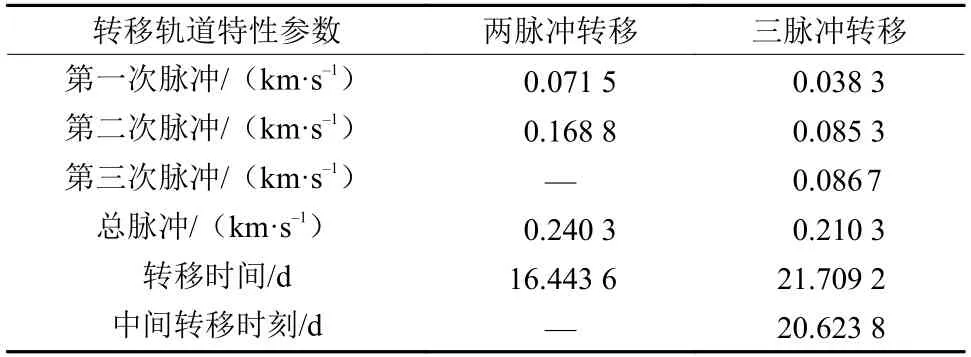
表8 L1点Halo轨道族–DRO轨道族的脉冲转移结果Table 8 Transfer impulses from L1 Halo family to DRO family

4.3 借助流形的转移轨道

对于借助平动点轨道流形的脉冲转移问题，仍然可将流形数据视为三体模型下的一类特殊轨道族。本文选取两种轨道转移场景进行仿真：①绕L1点Halo轨道流形到绕L2点Halo轨道的转移；② 绕L1点Halo轨道流形到DRO轨道的转移。

1）L1点Halo轨道流形到L2点Halo轨道的转移

选择振幅为48 320 km绕L1点Halo轨道的不稳定流形和振幅为52 900 km的绕L2点Halo轨道作为起始轨道和目标轨道，离散的轨道数据构成三维矩阵和二维矩阵，维度分别为：6 × 2 000 × 50和6 × 2 000。通过算法可求得两脉冲转移轨道分别如图10（a）所示，指标随迭代的变化曲线如图10（b）所示。

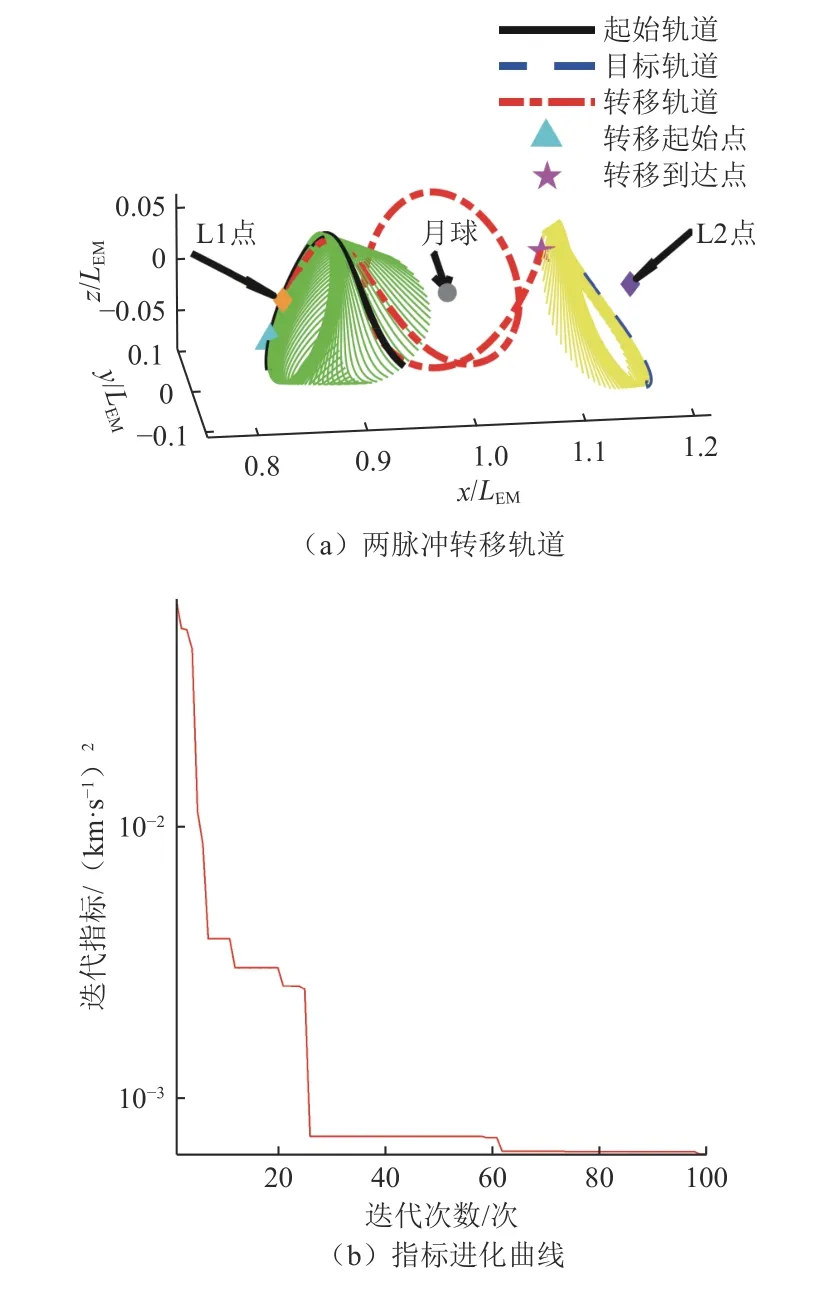
图10 L1 Halo流形–L2 Halo两脉冲转移Fig.10 Transfer from manifolds of L1 Halo to L2 Halo using two impulses

2）L1点Halo轨道流形到DRO轨道的转移

选择振幅为48 320 km绕L1点Halo轨道的不稳定流形和振幅为285 600 km的DRO作为起始轨道和目标轨道，离散的轨道数据构成三维矩阵和二维矩阵，维度分别为：6 × 2 000 × 50和6 × 2 000。采用两脉冲进行轨道转移，指标选择为能量最优。通过算法可求得转移轨道分别如图11（a）所示，指标随迭代的变化曲线如图11（b）所示。

由于扰动施加在平动点轨道的不同位置可生成不同的流形，其离散数据可认为与特殊轨道族类似。由图10（a）、图11（a）所示，算法通过两脉冲完成L1点Halo轨道的流形至L2点Halo轨道和DRO轨道的转移，同时实现起始点、目标点、中间脉冲点以及转移时间的选取。根据图10（b）、图11（b）可得，两转移轨道的指标随着算法迭代计算逐渐收敛，可得此算法对借助流形的转移轨道设计仍然适用。脉冲优化结果如表9所示。

表9 借助流形的脉冲转移结果Table 9 Impulse transfer by means of manifolds

根据4.1～4.3节仿真结果可得本文所提出的分层重构的建模方法能够适应各种不同特殊轨道之间的多脉冲转移问题，也具有添加其它约束条件的潜力（如月球借力中的高度约束和近月点约束）。另外，如3.3节中对算法初值的分析，本文仿真中选择所有脉冲矢量为 0矢量作为迭代初值，说明本算法无需对不同转移任务设计不同的脉冲初值，算法普适性较高。

4.4 对比仿真

文献[20]详细分析了地月空间中NRHO与DRO之间的两脉冲转移问题，并根据轨道特性设计了转移轨道的初值，文中关于初值的讨论可总结如下。

1）遍历搜索NRHO中的500个离散点作为起始点，DRO同样被离散为数百个点，从轨迹上的点到DRO离散点的最小距离被视为到DRO的近似距离；

2）选取出发脉冲前后速度的比值：假设出发脉冲与出发点速度平行，且比值范围在0.5～1.5；

3）两参数确定的轨迹将在最大传输时间内进行积分，使用无量纲单位为20，大约相当于87 d，分为200组进行遍历；

4）在搜索阶段，轨迹可能多次接近DRO，从每组到DRO的最小距离中选取所有的最小距离，并将传输轨迹和DRO上的相应点视为潜在的插入点。提取搜索参数、DRO上的潜在插入点和飞行时间作为初始猜测。然后，在每组中选择估计传输成本最低的前100个初始猜测，以供后续优化使用。

与文献[20]中选择相同振幅的NRHO与DRO分别作为起始轨道与目标轨道，同时转移时间也选择相同条件，参数如表10所示。将参数代入本文所提出的双层优化算法框架中，可得到转移轨道如图12所示，所需脉冲与文献数据的对比如表11所示。

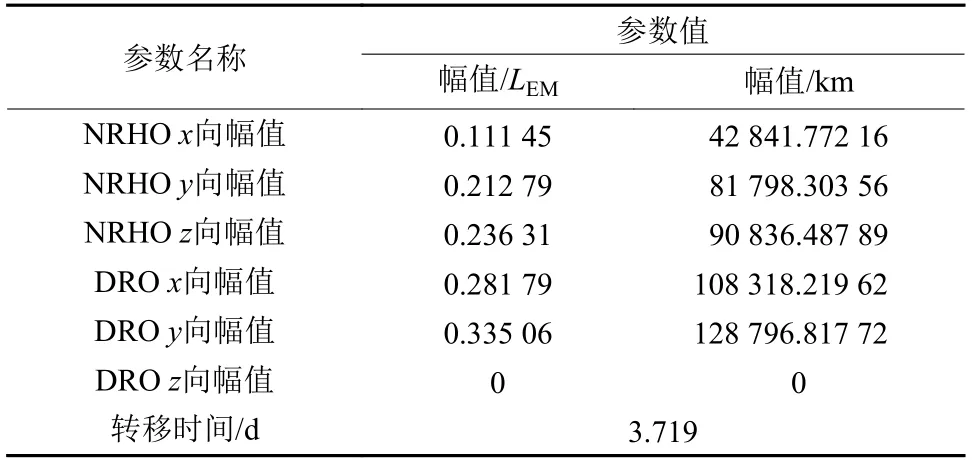
表10 对比仿真相关参数表Table 10 Parameters of comparative simulation

表11 脉冲结果对比Table 11 Comparison of transfer impulses

可见，在轨道与转移时间完全相同的仿真情况下，通过本文所提方法进行计算得到的转移脉冲可与文献数据达到更好的最优程度，且节省了约27 m/s的速度脉冲。这主要由于文献中所提初值设计方法有一定的局限性，在进行多个参数的选择时容易陷入局部最优情况，而本文通过对问题的分层建模求解，实现了更好的全局最优性。同时无需经过初值设计，也同样适用于其它轨道；文献中仅研究了两脉冲转移问题，所用初值设计方法也局限于两脉冲，本文所提方法同样适用于多脉冲转移，实现了更好的普适性。

5 结论

本文基于离散的轨道数据，在地月圆型限制性三体模型下提出了一种多脉冲转移轨道的设计方法。考虑起点与终点不固定、转移时间不固定、起始轨道与目标轨道可变化等多种不确定因素，通过拆分变量将最小脉冲问题重构为双层优化问题，设计了一种双层优化算法：上层兼顾了全局最优性和计算效率，并通过引入离散轨道数据约束实现了对多种类型轨道的普遍适用；下层考虑始末状态约束、时间约束、脉冲约束与脉冲点约束等实现最小脉冲问题的局部最优，同时避免算法对初值的敏感性。

仿真结果表明，本文所提出的对离散轨道数据进行始末状态约束能够适用于多种确定轨道、不同轨道族以及平动点轨道流形之间的相互转移，同时提出的双层优化算法也能够满足多种约束并实现多脉冲下的近似最小脉冲转移。对算法进一步拓展，也可对更高精度星历模型下的转移轨道进行计算。该研究成果为未来长期绕月探测、载人登月以及建设月球空间站等提供了有力的技术支持，通过优化的轨道设计，将为这些任务的执行提供更高的效率和可行性。未来的研究可以在本文基础上进一步探索，优化和改进该算法，以满足更复杂的转移需求，并拓展到其它三体问题和空间探索领域。